【算法】平衡二叉搜索树的左旋和右旋
树旋转是一种维护平衡树结构的重要操作,主要用于平衡二叉搜索树(如AVL树和红黑树)。树旋转分为左旋和右旋。
1. 树旋转的定义
左旋 (Left Rotation)
左旋操作将节点及其右子树进行调整,使其右子树的左子节点成为根节点,原根节点成为新根节点的左子节点。
定义:
- 假设一个节点
x有右子节点y,进行左旋时,以x为支点,将y提升为根节点,x变成y的左子节点。
示意图:
x y\ / \y ==> x z/ \ / \T2 z T1 T2
右旋 (Right Rotation)
右旋操作将节点及其左子树进行调整,使其左子树的右子节点成为根节点,原根节点成为新根节点的右子节点。
定义:
- 假设一个节点
y有左子节点x,进行右旋时,以y为支点,将x提升为根节点,y变成x的右子节点。
示意图:
y x/ / \x ==> T1 y/ \ / \T1 T2 T2 T3
2. 树旋转的Java代码实现
左旋代码 (Left Rotation)
class TreeNode {int value;TreeNode left;TreeNode right;TreeNode(int value) {this.value = value;this.left = null;this.right = null;}
}public TreeNode leftRotate(TreeNode x) {TreeNode y = x.right;TreeNode T2 = y.left;// Perform rotationy.left = x;x.right = T2;// Return new rootreturn y;
}
右旋代码 (Right Rotation)
public TreeNode rightRotate(TreeNode y) {TreeNode x = y.left;TreeNode T2 = x.right;// Perform rotationx.right = y;y.left = T2;// Return new rootreturn x;
}
3. 树旋转的优缺点
优点
- 保持平衡: 树旋转是平衡二叉树(如AVL树和红黑树)中保持平衡的核心操作,可以防止树退化成链表,提高查找、插入和删除操作的效率。
- 高效: 旋转操作的时间复杂度为O(1),即常数时间内完成。
- 提高性能: 通过保持树的平衡性,树旋转可以确保在最坏情况下操作的时间复杂度为O(log n)。
缺点
- 实现复杂: 树旋转的实现和维护相对复杂,需要仔细处理旋转过程中节点的连接和调整。
- 开销增加: 虽然单次旋转的时间复杂度为O(1),但在插入或删除节点时,可能需要进行多次旋转,这会增加操作的总开销。
- 维护难度: 对于平衡二叉树,如AVL树和红黑树,除了旋转操作,还需要维护其他信息(如高度、颜色),增加了代码复杂度。
总结
树旋转是维护平衡树结构的关键操作,通过旋转可以保持树的平衡性,从而提高查找、插入和删除操作的效率。尽管实现和维护有一定的复杂性,但其在提高树结构性能方面的作用非常显著,特别是在需要高效动态操作的场景下。
相关文章:

【算法】平衡二叉搜索树的左旋和右旋
树旋转是一种维护平衡树结构的重要操作,主要用于平衡二叉搜索树(如AVL树和红黑树)。树旋转分为左旋和右旋。 1. 树旋转的定义 左旋 (Left Rotation) 左旋操作将节点及其右子树进行调整,使其右子树的左子节点成为根节点…...

介绍Django Ninja框架
文章目录 安装快速开始特性详解自动文档生成定义请求和响应模型异步支持中间件支持测试客户端 结论 Django Ninja是一个基于Python的快速API开发框架,它结合了Django和FastAPI的优点,提供了简单易用的方式来构建高性能的Web API。 安装 使用以下命令安…...

使用uniapp内置组件checkbox-group所遇到的问题
checkbox-group属性说明 属性名类型默认值说明changeEventHandle <checkbox-group> 中选项发生改变触发change事件 detail { value:[选中的checkbox的value的数组] } 问题代码 <checkbox-group change"handleEVent()"><view style&qu…...

嵌入式学习记录5.23(超时检测、抓包分析)
目录 一.自带超时参数的函数 1.1 select函数 1.2 poll函数的自带超时检测参数 二、不带超时检测参数的函数 三、通过信号完成时间的设置 四、更新下载源 五、wireshark使用 5.1. 安装 5.2. wireshark 抓包 5.2.1 wireshark与对应的OSI七层模型 编辑5.2.2 包头分析 …...
Linux|如何在 awk 中使用流控制语句
引言 当您从 Awk 系列一开始回顾我们迄今为止介绍的所有 Awk 示例时,您会注意到各个示例中的所有命令都是按顺序执行的,即一个接一个。但在某些情况下,我们可能希望根据某些条件运行一些文本过滤操作,这就是流程控制语句的方法。 …...

OceanBase数据库诊断调优,与高可用架构——【DBA从入门到实践】第八期
在学习了《DBA从入门到实践》的前几期课程后,大家对OceanBase的安装部署、日常运维、数据迁移以及业务开发等方面应当已经有了全面的认识。若在实际应用中遇到任何疑问或挑战,欢迎您在OceanBase社区问答论坛中交流、讨论。此次,《DBA从入门到…...
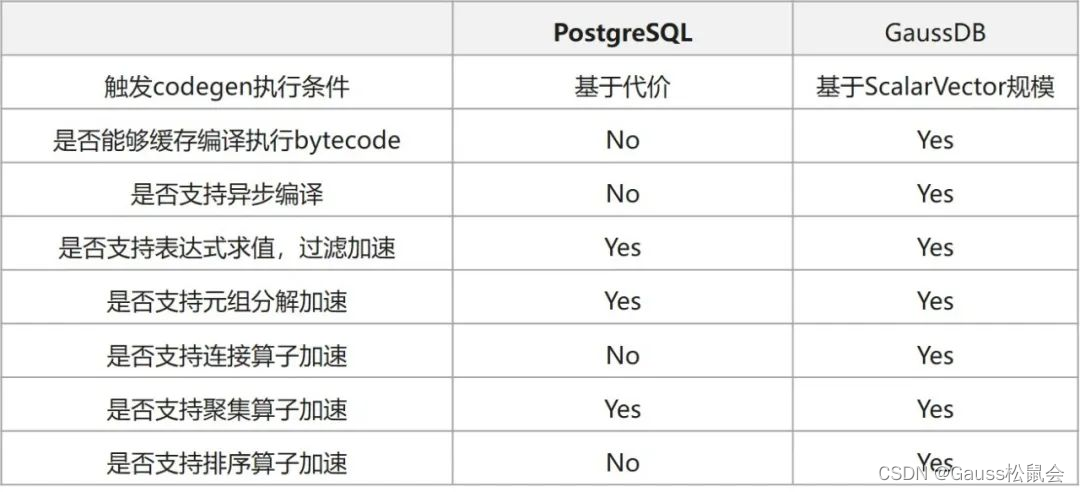
LLVM技术在GaussDB等数据库中的应用
目录 LLVM和数据库 LLVM适用场景 LLVM对所有类型的SQL都会有收益吗? LLVM在OLTP中就一定没有收益吗? GaussDB中的LLVM 1. LLVM在华为应用于数据库的时间线 2. GaussDB LLVM实现简析 3. GaussDB LLVM支持加速的场景 支持LLVM的表达式:…...

【SQL学习进阶】从入门到高级应用(三)
文章目录 ✨条件查询✨条件查询语法格式✨等于、不等于✨等于 ✨不等于 <> 或 ! ✨大于、大于等于、小于、小于等于✨大于 >✨大于等于 >✨小于 <✨小于等于 < ✨and✨or✨and和or的优先级问题✨between...and... 🌈你好呀!我是 山顶风…...

迷你手持小风扇哪个品牌续航强?五款强续航迷你手持小风扇推荐!
夏天就俩字儿:热和空调!太阳大得让人想躲,一出汗,感觉全身毛孔都在喊“太热啦”!这时空调简直是救命恩人啊,热得只想赖在屋里不出来。但出门总得面对大太阳,一出门就哗哗流汗。所以,…...
SpringBoot 微服务中怎么获取用户信息 token
SpringBoot 微服务中怎么获取用户信息 token 当我们写了一个A接口,这个接口需要调用B接口,但是B接口需要包含请求头内容,比如需要用户信息、用户id等内容,由于不在同一个线程中,使用ThreadLocal去获取数据是无法获取的…...

npm包-fflate
fflate 是一个快速、轻量级且纯JavaScript实现的压缩库,用于处理gzip、zlib和Deflate格式的数据压缩与解压缩。它专注于提供高性能的压缩算法实现,特别适合于浏览器环境及Node.js环境中使用,且不依赖任何外部库。fflate的优势在于其极小的体积…...

华为WLAN无线组网技术与解决方案
WLAN无线组网技术与解决方案 网络拓扑采用AP和AC旁挂式无线组网 配置思路: 1.让AP上线 1.1,使得AP能够获得IP地址 配置步骤: 1.把AC当作一个一个有管理功能的三层交换机 sys Enter system view, return user view with CtrlZ. [AC6605]vlan …...

闲鱼电商运营高级课程,一部手机学会闲鱼开店赚钱
课程下载:https://download.csdn.net/download/m0_66047725/89360471 更多资源下载:关注我。 课程内容: 10-9、怎么寻找优质的货源店铺.mp4 11-10、怎么去选择商品图片.mp4 12-11、商品图片的注意避免事项.mp4 13-12、怎么写标题.mp4 …...

Yann LeCun 和 Elon Musk 就 AI 监管激烈交锋
🦉 AI新闻 🚀 Yann LeCun 和 Elon Musk 就 AI 监管激烈交锋 摘要:昨天,Yann LeCun 和Elon Musk 在社交媒体就人工智能的安全性和监管问题展开激烈辩论。LeCun 认为目前对 AI 的担忧和监管为时过早,主张开放和共享。而…...

C++重点基础知识汇总大全
文章目录 一些基础知识点指针和引用 一些基础知识点 1、十进制的数字比较长的时候,可以加方便阅读到底是几位,输出的时候跟不加是一样的效果 // 十进制可以加 cout << 13890324 << endl; // 13890324 // 二进制前加0b cout << 0b111…...
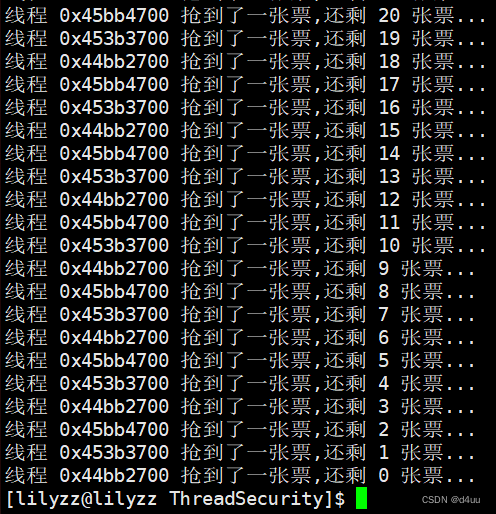
【Linux】线程安全及锁的使用
文章目录 前言一、锁1.定义一个锁变量2.pthread_mutex_init3.pthread_mutex_destroy4.pthread_mutex_lock/pthread_mutex_unlock5.静态变量锁和全局变量锁的初始化 二、问题描述及锁的运用三、RAII风格的锁 前言 临界资源: 在多个线程或进程间共享的资源. 临界区: 代码中访问临…...

深入解析绘图范式:面向对象与直接操作的较量
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 第一节:面向对象绘图的魅力 第二节:直接操作绘图模块的便捷性 第三…...

英特尔LLM技术挑战记录
英特尔技术介绍: Flash Attention Flash Attention 是一种高效的注意力机制实现,旨在优化大规模 Transformer 模型中的自注意力计算。在深度学习和自然语言处理领域,自注意力是 Transformer 架构的核心组件,用于模型中不同输入元…...

在 MFC 中 UNICODE 加 _T 与 L 长字符串,有什么区别?
在MFC(Microsoft Foundation Classes)和更广泛的Windows编程环境中,UNICODE宏用于指示程序应使用Unicode字符集(通常是UTF-16)来处理文本。当定义了UNICODE宏时,编译器和库函数会期待和处理宽字符ÿ…...

synopsys EDA 2016 合集 下载
包含如下安装包,如需安装服务也可联系我 FineSim_vL_2016.03 Laker201612 Library Compiler M-2016.12 Update Training PrimeTime M-2016.12 Update Training StarRC M-2016.12 Update Training SynopsysInstaller_v3.3 TSMC-65nm(OA) fm_vL-2016.03-SP1 fpga_vL-…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
