小白如何如何理解滑动窗口最大值问题python
文章目录
- 题目描述
- 思路
- 什么时候弹出元素
- 什么时候加入元素
- 代码示例和解释
题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
举例:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
思路
很容易想到暴力求解,遍历数据[i:i+k]取出max最大值即可,但是这种做法容易暴力超时,因此引出了自DIY的队列,主要关注的是什么时候弹出,什么时候加入队列
什么时候弹出元素
1.当遍历个数大于k的时候,弹出queue左侧==nums[i-k]
2.当队列最右侧元素小于nums[i],弹出右侧元素,因为他不可能是最大值了,队列内最多只有k个值,所以遍历到的这个元素才能成为最大值
什么时候加入元素
没遍历一次长度大于k的时候就加元素
代码示例和解释
from collections import deque
def max SlidingWindow(nums, k):queue = deque() # 双端都能插入删除的队列res = [] # 存放最后的结果# 把前面三个元素按需求加入到dequefor i in range(k):while queue and nums[i] > queue[-1]:queue.pop() # 弹出右边的元素,不可能成为最大值deque.append(nums[i])# 从k开始遍历后面的每个元素for i in range(k, len(nums)):# 只有遍历到的元素queue[0]等于nums[i-k]才需要弹出元素if queue and queue[0] == nums[i-k]:queue.popleft()while queue and queue[-1] < nums[i]:queue.pop()queue.append(nums[i])res.append(queue[0]) # 加入最大值return res
*[注意点]:queue内部的元素个数一定是小于等于k的,比如k = 3的时候,因为遍历到长度第4个元素,如果queue首元素和nums[i-k]元素相等就会有pop操作,即使不相等,其他需要pop()的元素也会被push的过程弹出,所以queue的长度始终不可能大于k
相关文章:

小白如何如何理解滑动窗口最大值问题python
文章目录 题目描述思路什么时候弹出元素什么时候加入元素 代码示例和解释 题目描述 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 举例: 输…...

Linux--进程间通信(2)(有名管道)
目录 1.原理 2.创建命名管道 3.使用命名通道实现简单的通信 4.使用创建的命名管道 1.原理 匿名管道没有名称,它们是通过句柄在父进程和子进程之间传递的。这意味着匿名管道只能用于具有父子关系的进程之间。 但如果程序之间没关系,那么这时候就要用…...
window自动启动bat文件
开机自动开启远程桌面, WinR 执行netplwiz 命令进入设置;取消勾选,可选择所需用户,点击应用,输入远程的密码即可 开机自动开启远程桌面, WinR 执行netplwiz 命令进入设置;取消勾选࿰…...
2024年蓝桥杯Web开发【大赛大纲】15届
一、 组别 Web应用开发分为:大学组和职业院校组。 每位选手只能申请参加其中一个组别的竞赛。各个组别单独评奖。 研究生和本科生只能报大学组。 其它高职高专院校可自行选择报任意组别。 二. 竞赛赛程 省赛时长:4小时。 决赛时长:4小…...
【vue-cli搭建vue项目的过程2.x】
vue-cli搭建vue项目 vue-cli搭建vue项目安装node安装vue-cli脚手架并创建项目安装 Ant Design Vue或element-ui(笔者使用Ant-design-vue组件,并全局引入)开发安装三方库包1、Package.json文件---引入如下package.json文件执行npm i或npm install命令即可下载如下依赖…...
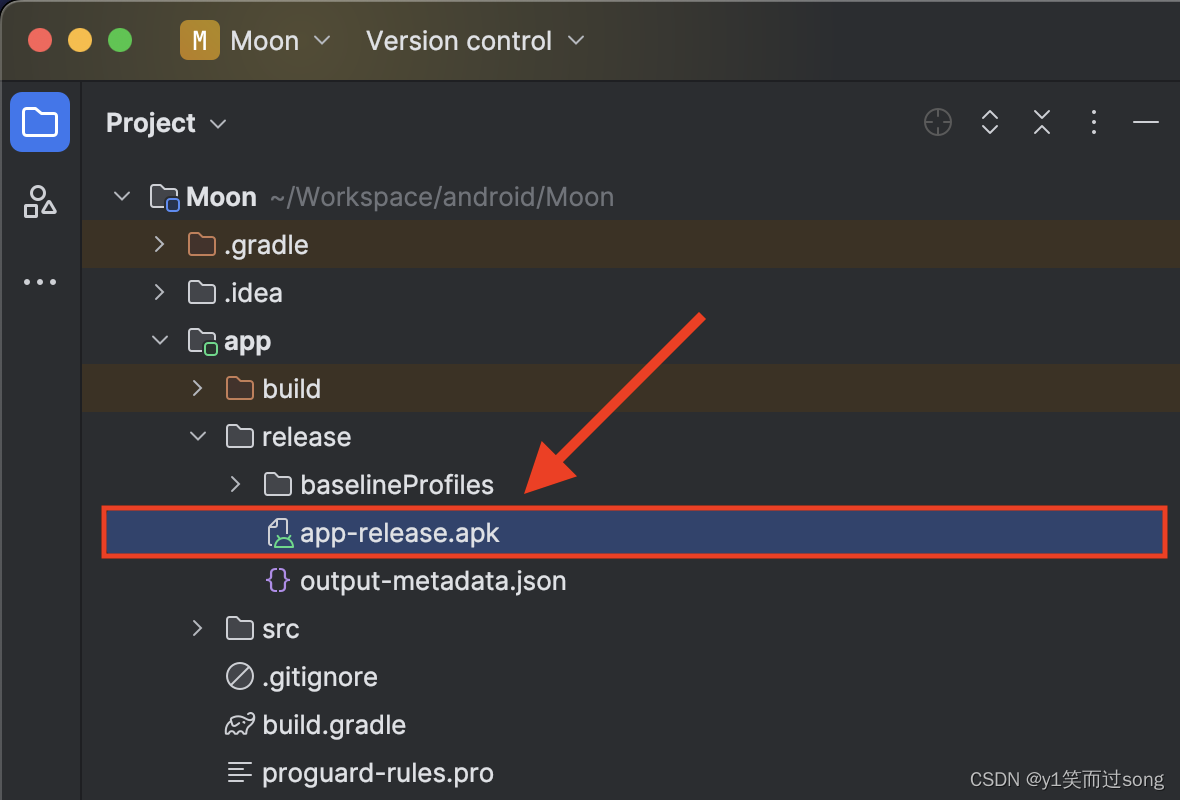
Android 生成正式版密钥库 KeyStore
步骤1:打开生成正式版密钥库设置 点击 Build 菜单,选择 Generate Signed App Bundle or APK: 这是打开后的样子: 步骤2:选择 APK Android App Bundle 是用于上架 Google Play 商店的。 正常情况下选择 APK。 选择…...
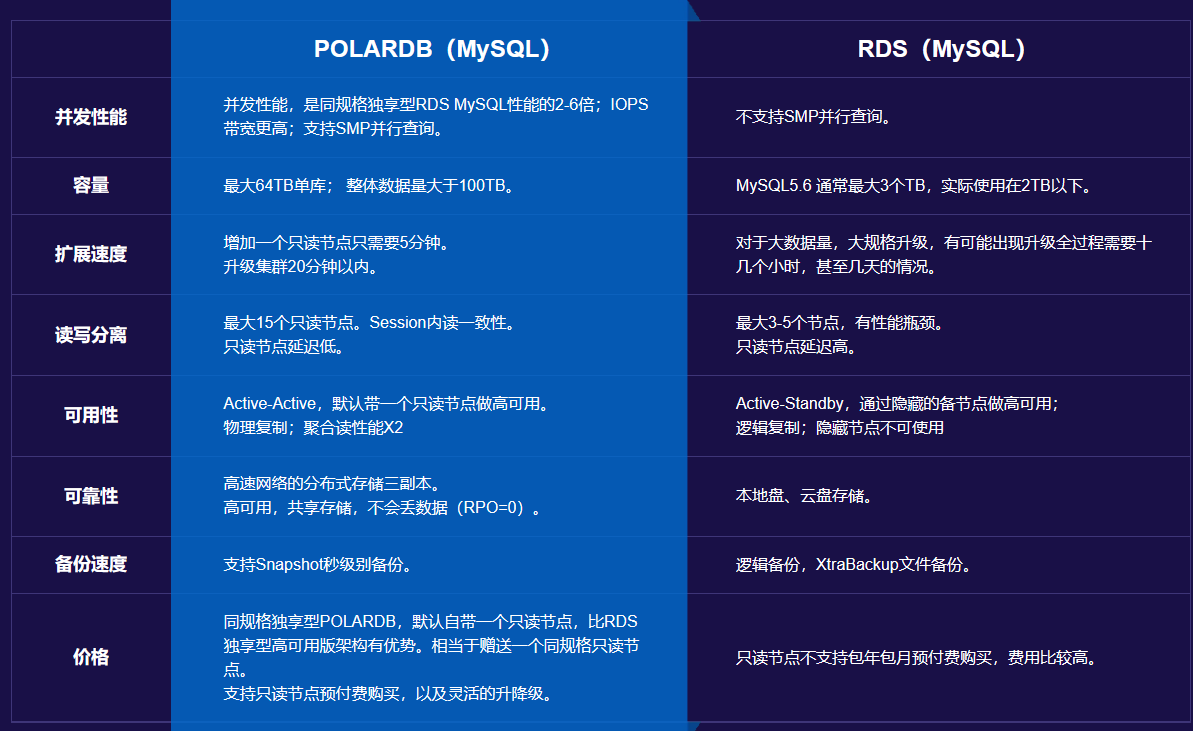
POLARDB:新零售用户MySQL上云最佳选择
什么是云数据库POLARDB? POLARDB是阿里云自主研发的最新一代RDS关系型数据库,是特别针对互联网场景设计的Cloud-Native 云原生数据库。POLARDB for MySQL版本,在提供100%兼容MySQL5.6/8.0的关系型事务处理ACID特性之上,能够提供完…...

PHP MySQL图解学习指南:开启Web开发新篇章
PHP曾经是最流行的Web开发语言,许多世界领先的网站(如Facebook、维基百科和WordPress)都是用它编写的。PHP运行在Web服务器端,通过使用存储在MySQL数据库中的数据,使得网站可以为每一位访问者显示不同的定制页面。书中采用简单、直观的图示化…...

uniapp一些问题解决
1.按钮边框如何去除? 参考博主:微信小程序按钮去不掉边框_微信小程序button去掉边框-CSDN博客文章浏览阅读1k次。最近在学uni-app,顺便自己写个小程序。左上角放了个button,可边框怎么也去不掉…原来微信小程序的按钮要去掉边框要…...

数字经济讲师培训师教授唐兴通谈新质生产力数字化转型高质量发展AI人工智能大模型大数据经信委大数据管理局
什么是数字经济? 数字经济是指通过数字技术将个人、企业、设备、数据和运营连接起来而产生的经济活动。它涵盖了互联网、移动技术、大数据和信息通信技术等多个行业和技术之间的在线连接和交易。 数字经济不同于传统经济,因为它依赖数字技术、在线交易…...

关于APM32F407配置串口DMA收发没有数据的问题记录
一.问题环境 整活了一套APM32F407的板子,用了APM32F4xx_SDK_V1.4的标准外设库,正在搭建移植底层BSP框架串口部分,BSP底层配置逻辑是从STM32F407移植过来的。DMA发送时才使能通道及配置外设地址及缓存大小。 串口1DMA配置过程如下&…...

基于python实现的深度学习web多格式纠错系统
基于python实现的深度学习web多格式纠错系统 开发语言:Python 数据库:MySQL所用到的知识:Django框架工具:pycharm、Navicat、Maven 系统功能实现 用户登录 登录功能是本系统一个非常重要的功能,这极大的保护了系统的安全。登录…...

UE5文件操作
首先在虚幻引擎中创建UMyBlueprintFunctionLibrary类,可以在该类中写我们重复利用的功能,并且这些功能不依赖于特定的游戏对象,方便全局调用。 1.文件的读取和写入 UFUNCTION(BlueprintCallable, Category "File")static bool lo…...

element plus 去掉select选择框的边框,并修改右侧图标
1.去掉选择框边框 ::v-deep .el-select__wrapper{ box-shadow: none; } ::v-deep .is-hovering{ box-shadow: none !important; }2.修改选择框右侧图标 新建CaretBottom.vue文件内容: <template><el-icon><CaretBottom /></el-icon> <…...
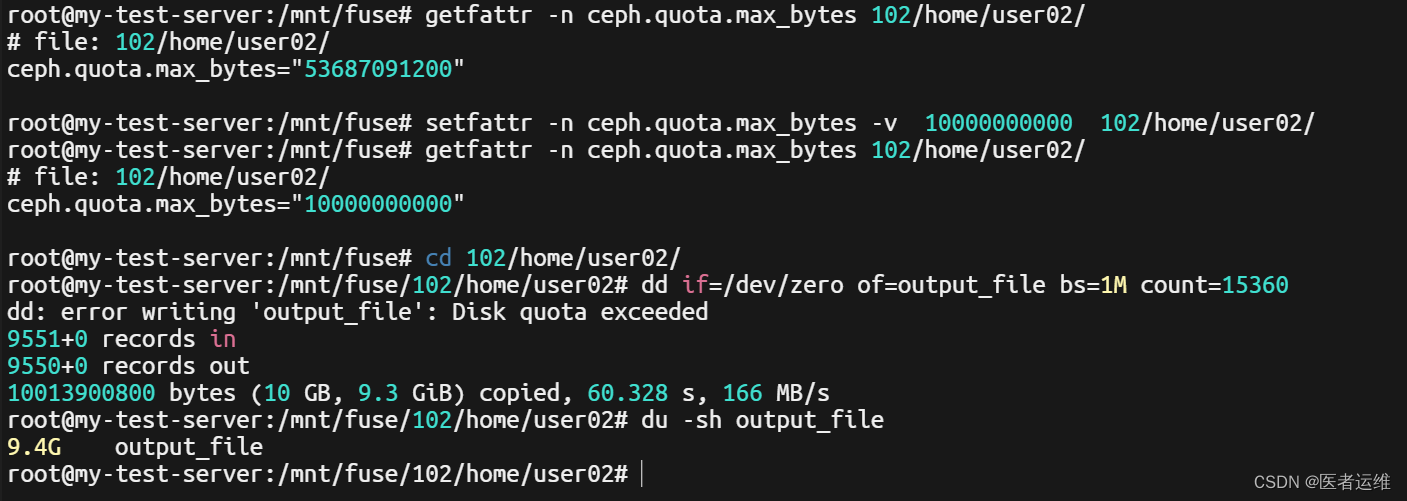
Ceph KernelFuse GetSet Quota
Kernel fuse set示例...
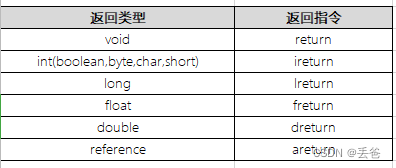
JVM学习-字节码指令集(二)
对象的创建与访问指令 创建指令 虽然类实例和数组都是对象,但Java虚拟机对类实例和数组的创建和操作使用了不同的字节码指令创建类实例指令:new 它接收一个操作数,指向常量池的索引,表示要创建的类型,执行完成后&am…...

解密网络流量监控:优化IT运维的利器
引言: 在当今数字化时代,网络流量监控是维护网络稳定与业务连续性的关键。作为一名资深网络工程师,我将分享一些关于网络流量监控的重要知识,并探讨如何在IT运维中运用这一工具优化网络性能,确保业务的顺畅进行。 1. 网…...
)
oracle 分区表常用语句(2)
给分区表增加分区 第一种不存在MAXVALUE(直接添加即可) ALTER TABLE T6 ADD PARTITION P5 VALUES LESS THAN(TO_DATE( 2018-08-01 00:00:00, SYYYY-MM-DD HH24:MI:SS, NLS_CALENDARGREGORIAN));第二种存在MAXVALUE alter table T6 split PARTITION P4 at(TO_DAT…...

Python函数式编程进阶:用函数实现设计模式
文章目录 函数式编程进阶:用函数实现设计模式案例实现:构建“策略”模式使用函数实现”策略“模式享元 选择最佳策略:简单的方式 globals关键字 函数式编程进阶:用函数实现设计模式 案例实现:构建“策略”模式 策略模…...
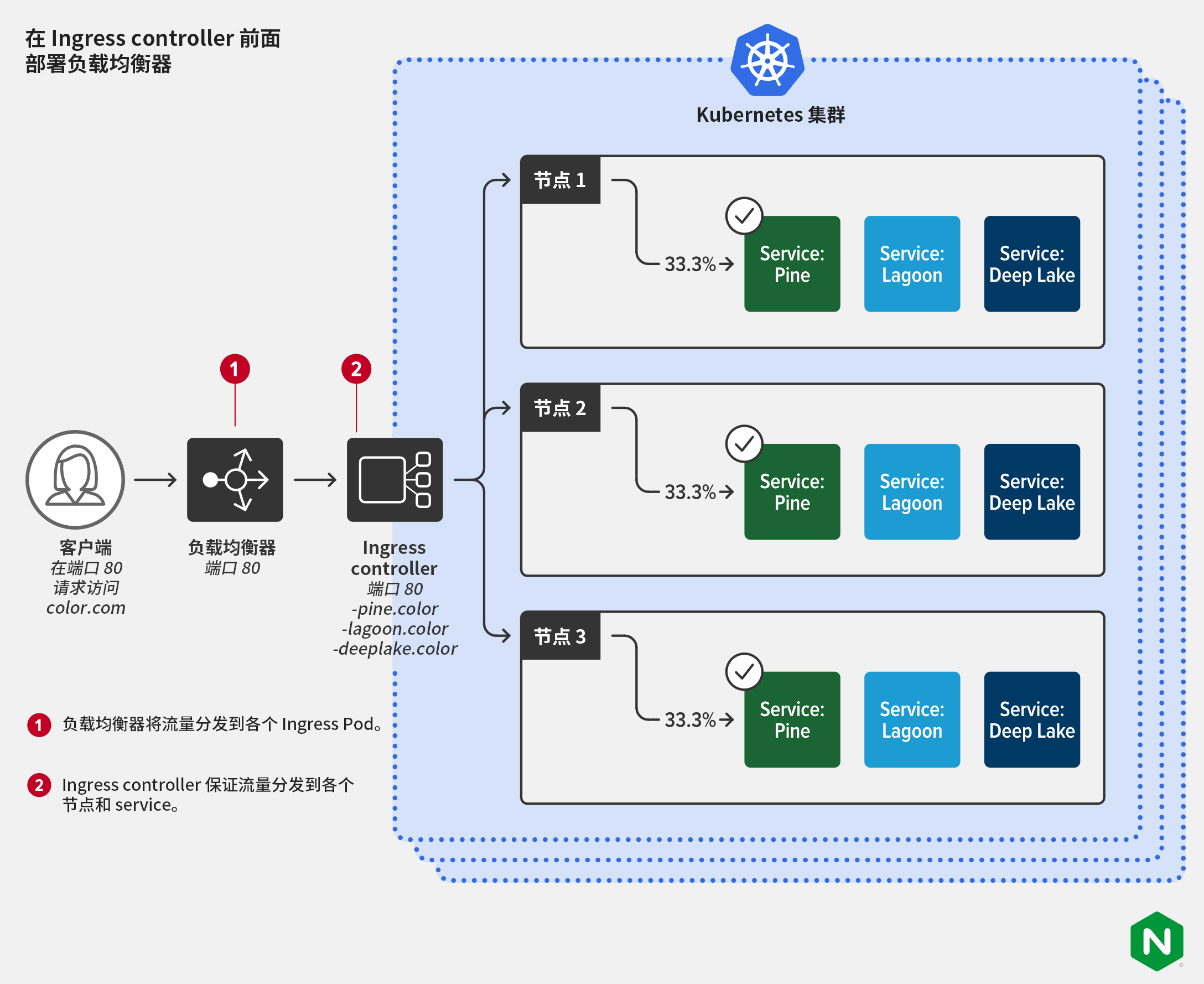
Ingress controller:Kubernetes 的瑞士军刀
原文作者:Brian Ehlert of F5 原文链接:Ingress controller:Kubernetes 的瑞士军刀 转载来源:NGINX 中文官网 NGINX 唯一中文官方社区 ,尽在 nginx.org.cn 许多人认为 Ingress controller(Ingress 控制器&…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
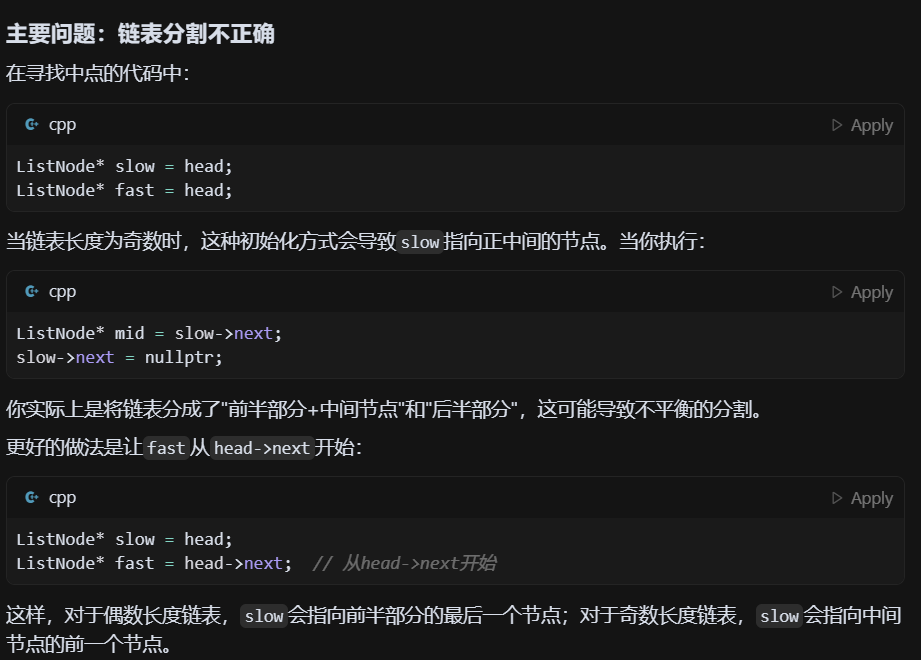
LeetCode - 148. 排序链表
目录 题目 思路 基本情况检查 复杂度分析 执行示例 读者可能出的错误 正确的写法 题目 148. 排序链表 - 力扣(LeetCode) 思路 链表归并排序采用"分治"的策略,主要分为三个步骤: 分割:将链表从中间…...

【芯片仿真中的X值:隐藏的陷阱与应对之道】
在芯片设计的世界里,X值(不定态)就像一个潜伏的幽灵。它可能让仿真测试顺利通过,却在芯片流片后引发灾难性后果。本文将揭开X值的本质,探讨其危害,并分享高效调试与预防的实战经验。 一、X值的本质与致…...
