贝叶斯算法:机器学习中的“黄金法则”与性能提升之道
👀传送门👀
- 🔍机器学习概述
- 🍀贝叶斯算法原理
- 🚀贝叶斯算法的应用
- ✨文本分类
- ✨医疗系统
- 💖贝叶斯算法优化
- ✨贝叶斯算法优化的主要步骤
- ✨贝叶斯算法优化的优点
- ✨贝叶斯算法优化的局限性
- 🚗贝叶斯算法在机器学习中的优势
- 🚲贝叶斯算法未来发展趋势
机器学习作为人工智能的核心领域,旨在使计算机能够模拟人类的学习过程,通过经验自动改进性能。在机器学习的众多算法中,贝叶斯算法以其独特的概率推理方式脱颖而出,广泛应用于文本分类、自然语言处理、垃圾邮件过滤等领域。本文将详细介绍机器学习贝叶斯算法的基本概念、原理、应用、代码实现以及算法优化,并探讨其在机器学习中的作用及未来发展趋势。

🔍机器学习概述
机器学习是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析等多门学科。其目标是通过计算机模拟人类的学习行为,以获取新的知识或技能,并重新组织已有的知识结构,使计算机能够自动改进性能。机器学习的主要应用包括图像和语音识别、自然语言处理、推荐系统、金融风控、医疗健康、自动驾驶、工业生产等。
🍀贝叶斯算法原理

贝叶斯算法是一种基于贝叶斯定理的机器学习方法,用于估计模型参数和进行概率推断。其核心思想是利用已知的先验概率和条件概率来更新我们对某个事件发生的概率的估计。在机器学习中,贝叶斯算法通常用于分类问题,通过计算数据属于不同类别的概率来进行分类。
🚀贝叶斯算法的应用
✨文本分类
贝叶斯分类器在文本分类中表现出色,特别是因为其假设特征之间是相互独立的。在实际应用中,可以使用朴素贝叶斯分类器对新闻、邮件等文本数据进行分类。代码实现通常涉及数据预处理、特征提取、模型训练和预测等步骤。
示例代码(Python):
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB # 加载数据集
news = fetch_20newsgroups(subset='all')
X, y = news.data, news.target # 数据预处理和特征提取
vectorizer = CountVectorizer()
X_counts = vectorizer.fit_transform(X) # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_counts, y, test_size=0.25, random_state=42) # 使用朴素贝叶斯分类器进行训练和预测
clf = MultinomialNB()
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
print("Accuracy:", score)
✨医疗系统

贝叶斯算法在医疗诊断中的应用通常涉及对医疗数据的分析,以预测患者可能患有的疾病。以下是一个简化的代码示例,说明如何使用朴素贝叶斯分类器(Naive Bayes Classifier)进行医疗诊断的模拟。
假设我们有一个关于患者症状和诊断结果的数据集,其中包含了多个特征和对应的疾病标签。我们将使用Python的scikit-learn库中的朴素贝叶斯分类器来训练模型,并对新的患者数据进行预测。
# 导入必要的库
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
import pandas as pd # 假设我们有一个关于医疗诊断的数据集(这里使用scikit-learn的模拟数据代替)
# 特征可能包括年龄、体温、血压等,标签是疾病类型
X, y = make_classification(n_samples=1000, n_features=4, n_informative=2, n_redundant=0, random_state=42) # 假设我们已经将数据集转换为Pandas DataFrame,以便更好地理解和操作
# 这里我们只是简单地使用NumPy数组作为示例
# df = pd.DataFrame(X, columns=['feature1', 'feature2', 'feature3', 'feature4'])
# df['diagnosis'] = y # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 使用高斯朴素贝叶斯分类器进行训练
gnb = GaussianNB()
gnb.fit(X_train, y_train) # 对测试集进行预测
y_pred = gnb.predict(X_test) # 计算预测精度
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy) # 假设我们有一个新的患者数据
new_patient = [[45, 37.2, 120, 80]] # 年龄, 体温, 收缩压, 舒张压 # 对新患者进行预测
new_patient_diagnosis = gnb.predict(new_patient)
print("Predicted diagnosis for the new patient:", new_patient_diagnosis) # 在实际应用中,我们可能需要将这些预测结果与医生的专业知识相结合,以做出最终的诊断决策。
💖贝叶斯算法优化
贝叶斯优化是一种基于贝叶斯定理的全局优化算法,适用于目标函数难以计算或计算成本较高的情况。其核心思想是通过建立一个目标函数的概率模型来指导搜索过程,从而找到使目标函数取得最优值的参数配置。与网格搜索和随机搜索相比,贝叶斯优化能够智能地选择评估点,处理复杂目标函数,并在较少的迭代次数内找到接近最优解的参数配置。
✨贝叶斯算法优化的主要步骤

- 建立目标函数模型:
- 选择合适的高斯过程模型(如高斯过程回归GPR或高斯过程分类GPC)作为目标函数的先验模型。
- 选取采样点:
- 利用贪心策略、置信区间策略等,根据先验模型选择下一个采样点,以尽可能减少目标函数的不确定性。
- 观测目标函数:
- 在选取的采样点处计算目标函数的值,并添加到已观测数据集中。
- 更新模型:
- 利用已观测的数据集更新先验模型,获得后验模型。后验模型可以提供目标函数的预测值及其不确定性。
- 迭代优化:
- 重复上述步骤,直到达到预设的迭代次数或满足其他停止条件。
✨贝叶斯算法优化的优点
- 高效性:贝叶斯优化方法能够充分利用目标函数的先验信息,在较少的迭代次数下找到较优解,大幅度减少计算量。
- 可解释性:通过建立概率模型,贝叶斯优化方法可以直观地解释模型的不确定性和预测结果的可靠性。
- 鲁棒性:在处理噪声较大、非凸的优化问题时,贝叶斯优化方法表现出较强的鲁棒性。
- 智能选择评估点:能够基于历史观测结果智能地选择下一个评估点,提高搜索效率。
- 处理复杂目标函数:能够处理多峰、非凸等复杂的目标函数,适用于各种应用场景。
✨贝叶斯算法优化的局限性
- 高计算复杂度:在每一次迭代中,贝叶斯优化方法都需要计算目标函数和更新模型,计算复杂度较高,特别是在高维问题和大规模数据集上。
- 对先验知识的依赖:贝叶斯优化方法的效果在很大程度上依赖于先验模型的选择和准确性。如果先验模型不准确或不适合目标函数,优化效果可能会受到影响。
🚗贝叶斯算法在机器学习中的优势

贝叶斯算法在机器学习中具有一系列显著的优势,这些优势使得它在处理某些任务时表现突出:
-
增量学习:贝叶斯算法支持增量学习,即它可以在新的数据到来时,不需要重新训练整个模型,而只需要根据新的数据更新模型的参数。这使得贝叶斯算法在处理数据流或实时数据时非常有效,因为它可以快速地适应新的变化。
-
处理不确定性:贝叶斯算法基于概率论,因此它能够自然地处理不确定性。在分类任务中,贝叶斯算法不仅可以输出最可能的类别,还可以给出该类别的概率,这对于需要了解预测可靠性的应用场景非常有用。
-
特征独立性假设:尽管朴素贝叶斯分类器假设特征之间是独立的,这在现实中很少成立,但这个假设大大简化了计算,使得朴素贝叶斯分类器在许多情况下都能取得良好的性能。此外,即使特征之间不是完全独立的,朴素贝叶斯分类器通常也能给出一个相当好的基线性能。
-
数学可解释性强:贝叶斯算法的推导过程基于贝叶斯定理,具有坚实的数学基础,因此其决策过程相对容易理解和解释。这使得贝叶斯算法在需要可解释性的应用中(如医疗诊断、法律决策等)特别有用。
-
避免过拟合:由于贝叶斯算法是基于概率的,它天然地具有避免过拟合的能力。这是因为在计算后验概率时,贝叶斯算法会考虑到先验概率(即数据的整体分布),这有助于防止模型过于关注训练数据中的噪声或异常值。
-
可扩展性:贝叶斯算法可以很容易地扩展到多类别分类问题,只需要为每个类别计算一个后验概率即可。此外,贝叶斯算法也可以很容易地处理具有连续特征的问题,只需要使用适当的概率密度函数(如高斯分布)即可。
然而,尽管贝叶斯算法具有这些优势,但它也有一些局限性,如朴素贝叶斯分类器的特征独立性假设可能不成立,以及对于复杂的模型(如深度神经网络),贝叶斯推断可能变得非常困难。但随着研究的深入和技术的发展,我们相信这些问题将会逐渐得到解决。
🚲贝叶斯算法未来发展趋势

贝叶斯算法在机器学习中扮演着重要角色,为分类问题提供了有效的解决方案。其独特的概率推理方式使得贝叶斯算法在处理不确定性和小样本数据时具有优势。随着大数据时代的到来,贝叶斯算法在医疗、金融、推荐系统等领域的应用将更加广泛。未来,贝叶斯算法将与其他机器学习算法结合,形成更加复杂和高效的模型,以应对更加复杂和多样化的任务。同时,随着计算能力的提升和算法的优化,贝叶斯算法在处理大规模数据集和复杂模型时的性能将得到进一步提升。
相关文章:

贝叶斯算法:机器学习中的“黄金法则”与性能提升之道
👀传送门👀 🔍机器学习概述🍀贝叶斯算法原理🚀贝叶斯算法的应用✨文本分类✨医疗系统 💖贝叶斯算法优化✨贝叶斯算法优化的主要步骤✨贝叶斯算法优化的优点✨贝叶斯算法优化的局限性 🚗贝叶斯算…...
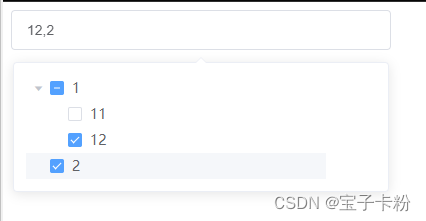
element-ui 实现输入框下拉树组件(2024-05-23)
用element-ui的 el-input,el-tree,el-popover组件组合封装 import url("//unpkg.com/element-ui2.15.14/lib/theme-chalk/index.css"); <script src"//unpkg.com/vue2/dist/vue.js"></script> <script src"//…...

Nginx 相关使用
一、 Nginx 相关使用。 相关命令 启动 nginx start nginx立即停止 nginx nginx -s stop平缓停止 nginx(已有请求不会意外停止) nginx -s quit重新加载配置文件 nginx -s reload二、Nginx conf 配置文件详解 参考文章皮卡丘的猫 server 配置项 server 可…...
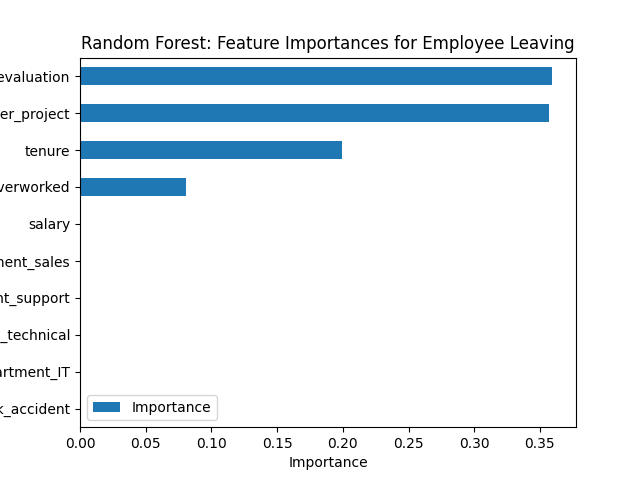
基于Python实现 HR 分析(逻辑回归和基于树的机器学习)【500010104】
介绍 数据集说明 此数据集包含与员工有关的综合属性集合,从人口统计细节到与工作相关的因素。该分析的主要目的是预测员工流动率并辨别导致员工流失的潜在因素。 在这个数据集中,有14,999行,10列,以及这些变量:满意度…...

5月岚庭工人大会“安全就是效率、形象即是品质”
2024年5月18日、19日岚庭一月一期的“产业工人大会”和“工程大会”圆满举行初夏正当时,此次大会主要围绕“安全”与“形象”展开六场专题培训只为精益求精产业工人和装修管家全体到场。 岚庭 以绝对【安全】护家护园 安全就是生命,违章就是事故&#x…...

Flutter 中的 MouseRegion 小部件:全面指南
Flutter 中的 MouseRegion 小部件:全面指南 在 Flutter 中,MouseRegion 是一个非常有用的小部件,它允许你为部件添加鼠标事件(如点击、悬停、离开等)。这在开发需要处理鼠标交互的应用时尤为重要。本文将详细介绍 Mou…...
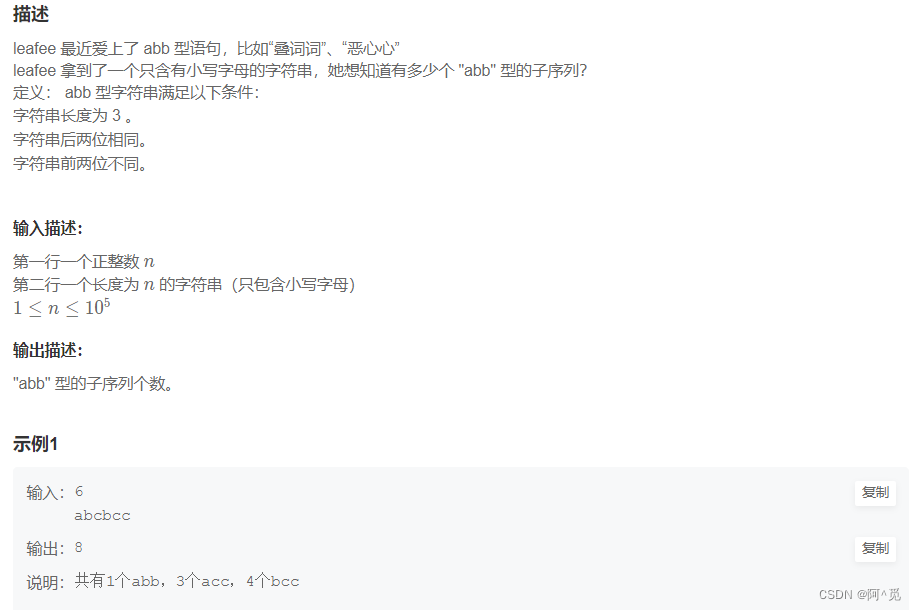
C++笔试强训day36
目录 1.提取不重复的整数 2.【模板】哈夫曼编码 3.abb 1.提取不重复的整数 链接https://www.nowcoder.com/practice/253986e66d114d378ae8de2e6c4577c1?tpId37&tqId21232&ru/exam/oj 按照题意模拟就行,记得从右往左遍历 #include <iostream> usi…...

网络通信过程的技术分析
网络通信过程的技术分析 目录 网络通信过程的技术分析 一、引言 二、网络通信基础 三、通信协议 四、数据传输过程 五、网络设备与通信 六、网络安全与通信 七、高级网络通信概念 八、结论 一、引言 网络通信是现代计算机网络中的核心活动,它涉及多个层面的…...
一篇文章搞懂二叉树
文章目录 DP 树叶的度树的度节点的层次节点的祖先节点的子孙双亲节点或父节点 树的表示孩子兄弟表示法双亲表示法树和非树树的应用 二叉树满二叉树完全二叉树推论二叉树的存储以数组的方式以链表的方式堆(Heap)堆的分类大根堆和小根堆的作用 二叉树的遍历DFS和BFS DP 动态规划…...

python——__future__模块
__future__模块是Python的一个特殊内建模块,它提供了一种方式来让程序员在当前版本的Python中使用未来版本的语言特性,从而帮助代码实现向前兼容。这意味着,即使你正在使用的是旧版本的Python,也可以通过导入__future__模块中的某…...
开源一个工厂常用的LIMS系统
Senaite是一款强大且可靠的基于Web的LIMS/LIS系统,采用Python编写,构建在Plone CMS基础架构之上。该系统处于积极开发阶段,在灵活的定制空间中为开发人员提供了丰富的功能。其中,Senaite在处理REST的JSON API上做得出色࿰…...

SpringBoot项目中redis序列化和反序列化LocalDateTime失败
实体类中包含了LocalDateTime 类型的属性,把实体类数据存入Redis后变成这样: 此时,存入redis不会报错,但是从redis获取的时候,会报错: com.fasterxml.jackson.databind.exc.InvalidDefinitionException: Ca…...

linux怎么查询远程管理卡型号
在Linux中,要查询远程管理卡(通常是服务器主板上的集成芯片,如iDRAC、iLO、BMC等)的型号,可以使用一些特定厂商的工具,或者通过IPMI(Intelligent Platform Management Interface)来实…...
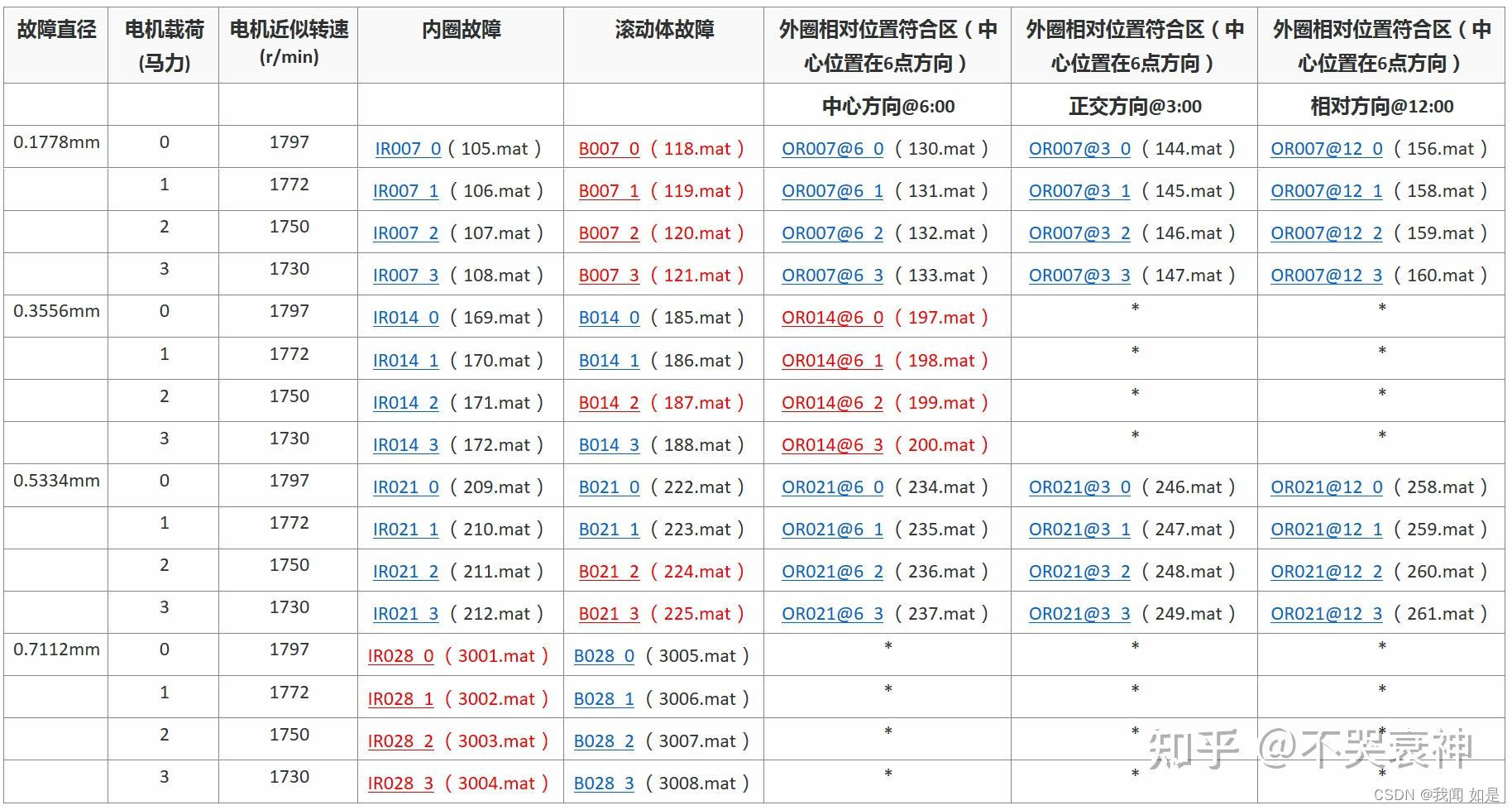
西储大学数据集学习
数据集下载地址:CWRU凯斯西储大学轴承数据数据集——附:下载链接_西储大学轴承数据集下载-CSDN博客 最近研究故障诊断,先对使用比较多的西储大学数据集研究。以资料【1】中的内容展开研究。 1、轴承的结构 轴承分为外圈、内圈、保持架和滚珠…...
《web应用技术》第九次作业
一、将前面的代码继续完善功能 1.采用XML映射文件的形式来映射sql语句; <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE mapper PUBLIC "-//mybatis.org//DTD Mapper 3.0//EN" "http://mybatis.org/dtd/mybatis…...

dockerfile关键字
参考:59_Dockerfile保留字简介_哔哩哔哩_bilibili FROM 作用:指定基础镜像,即在这个基础镜像上构建新镜像,如下所示,表示在ubuntu20.04镜像的基础上构建新镜像 FROM ubuntu:20.04 MAINTAINER 作用:镜像…...
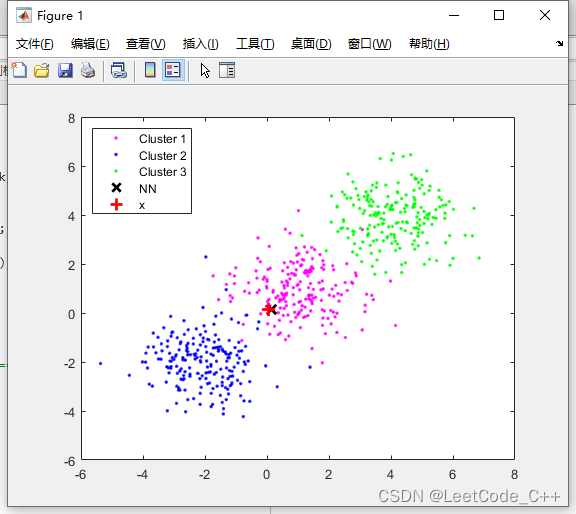
MATLAB分类与判别模型算法: 快速近邻法(FastNN)分类程序【含Matlab源码 MX_005期】
算法思路介绍: 1. 数据准备阶段: 生成一个合成数据集 X,其中包含三个簇,每个簇分布在不同的区域。 定义聚类层数 L 和每个层次的子集数量 l。 2. 聚类阶段: 使用K均值聚类算法将初始数据集 X 分成 l 个簇。…...

css卡片翻转 父元素翻转子元素不翻转效果
css卡片翻转 父元素翻转子元素不翻转效果 vue <div class"moduleBox"><div class"headTitle"><span class"headName">大额案例</span></div><div class"moduleItem"><span class"module…...

解决文件传输难题:如何绕过Gitee的100MB上传限制
引言 在版本控制和代码托管领域,Gitee作为一个流行的平台,为用户提供了便捷的服务。然而,其对单个文件大小设定的100MB限制有时会造成一些不便。 使用云存储服务 推荐理由: 便捷性:多数云存储服务如: Dro…...

零基础学Java第二十三天之网络编程Ⅱ
1. InetAddress类 用来表示主机的信息 练习: C:\Windows\system32\drivers\etc\ hosts 一个主机可以放多个个人网站 www.baidu.com/14.215.177.37 www.baidu.com/14.215.177.38 www.taobao.com/183.61.241.252 www.taobao.com/121.14.89.253 2. Socket 3.…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...

mq安装新版-3.13.7的安装
一、下载包,上传到服务器 https://github.com/rabbitmq/rabbitmq-server/releases/download/v3.13.7/rabbitmq-server-generic-unix-3.13.7.tar.xz 二、 erlang直接安装 rpm -ivh erlang-26.2.4-1.el8.x86_64.rpm不需要配置环境变量,直接就安装了。 erl…...

信息收集:从图像元数据(隐藏信息收集)到用户身份的揭秘 --- 7000
目录 🌐 访问Web服务 💻 分析源代码 ⬇️ 下载图片并保留元数据 🔍 提取元数据(重点) 👤 生成用户名列表 🛠️ 技术原理 图片元数据(EXIF 数据) Username-Anarch…...

【笔记】PyCharm 使用问题反馈与官方进展速览
#工作记录 https://youtrack.jetbrains.com/issue/IJPL-190308 【笔记】记一次PyCharm的问题反馈_the polyglot context is using an implementation th-CSDN博客 【笔记】与PyCharm官方沟通解决开发环境问题-CSDN博客 与 JetBrains 官方沟通记录(PyCharm 相关问题…...
