算法的时间复杂度(详解)
前言:
算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为 输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果
一、算法效率
1.1 如何衡量一个算法的好坏
如何衡量一个算法的好坏呢?比如对于以下斐波那契数列:
long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
1.2 算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般 是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
复杂度在校招中的考察
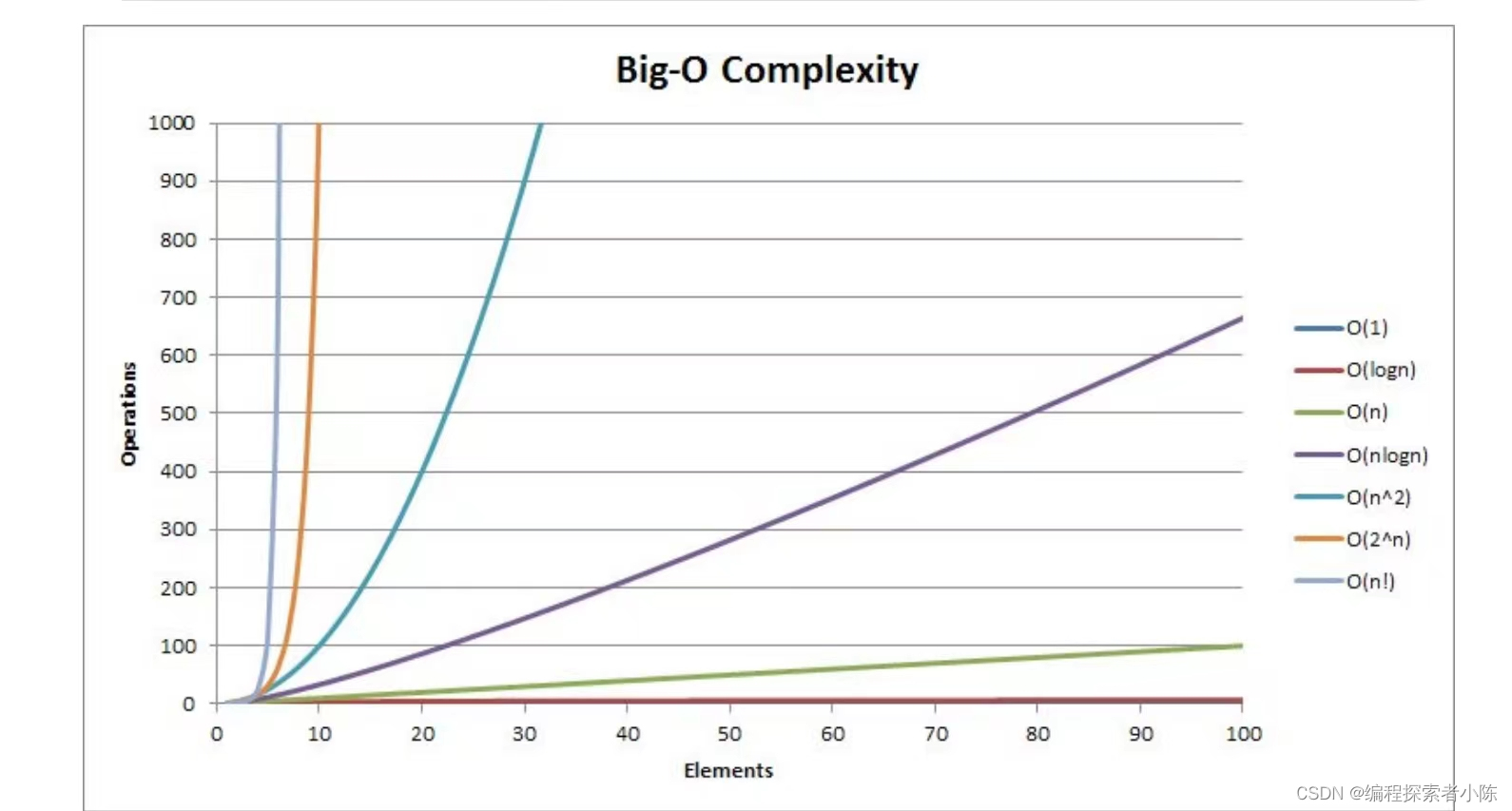
常见复杂度对比

二、时间复杂度
2.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一 个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个 分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
2.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
O(N^2)
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
三、常见时间复杂度计算举例
实例1:
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)
实例2:
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
实例3:
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}基本操作执行了100次,通过推导大O阶方法,时间复杂度为 O(1)
注:O(1)代表常数次
实例4:
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );我们分析一下
while (*str)
{if (*str == charcter)return str;else++str;
}基本操作执行最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)
实例5:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
基本操作执行最好N次,最坏执行了N*(N-1)/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N^2)
实例6:
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}分析二分查找的时间复杂度:

查找区间的变化:
N
N/2
N/4
N/8
……1
二分查找什么情况下最坏?查找区间只剩一个数,或者找不到,也就是:N/2/2…/2 = 1
查找了多少次,就是除了多少个2,假设查找了x次 2^x = N
那么查找次数为:x=logN(底数忽略不写)
则时间复杂度: O(logN)
因为写的时候需要支持专业公式,否则不好写底数,时间复杂度当中,为了方便,logN可以省略底数直接写成logN,其他底层不能省略(其他底数也很少出现)
实例7:
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}
递归时间复杂度:所有递归调用次数累加(等差数列)
通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。

实例8:
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
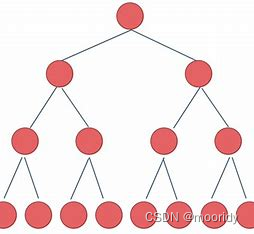
如下图所示:每次递归都是以2倍的形式增长,累加求和,我们可以使用等比数列错位相减法
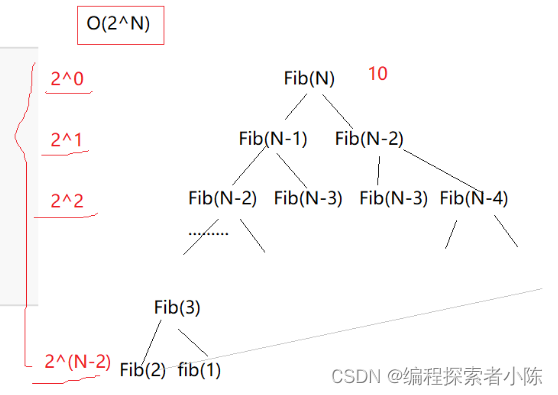

计算分析发现基本操作递归了2^N次,时间复杂度为O(2^N)。
这种算法基本上是废了,只有理论意义,实践中太慢了。
四、复杂度的OJ练习
1.消失的数字
OJ链接:消失的数字
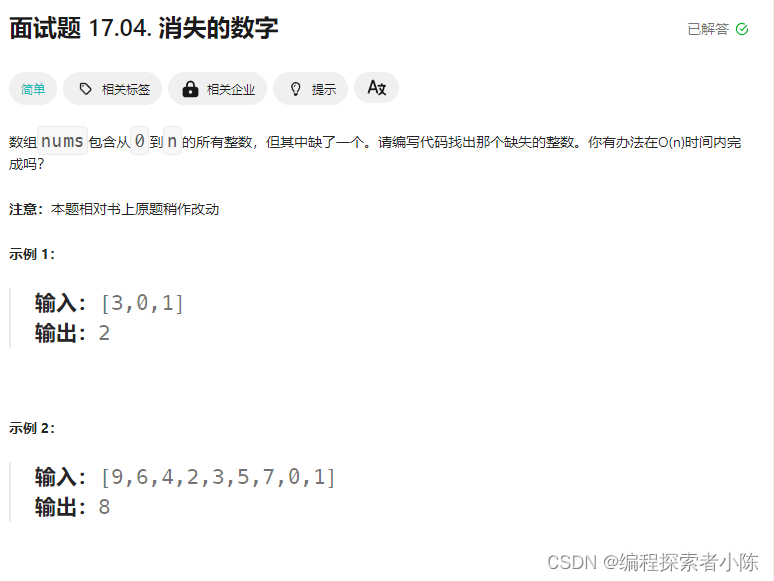
思路一:先排序,再依次查找,如果下一个值不等于前一个+1,下一个值就是消失数字,如果我们使用冒泡排序进行排序,就不符合题目要求了,因为它的时间复杂度是O(N^2)
思路二:求和0到N,再依次减去数组中的值,剩下的那个值就是消失数字,累加的时间复杂度为O(N),如果N的数字比较大可能会导致栈溢出。
代码如下:

思路三:我们可以使用异或,把数组中0到N的元素全部异或起来,相同为0相异为1,最后那个数字就是消失的数字,这样还可以防止栈溢出
代码如下:
int missingNumber(int* nums, int numsSize)
{int x = 0;int N = numsSize;for(int i = 0;i<numsSize;i++){x^=nums[i];}for(int j = 0;j<=numsSize;j++){x^=j;}return x;
}2.轮转数组
OJ链接:轮转数组

思路一:先写出旋转一次的函数,在调用k次,k的真实旋转次数为k%=numsSize
代码如下:

但是超出时间限制了

我们分析一下:
最坏情况 :k%N等于N-1 -> O(N^2)
最好情况:k%N等于0
时间复杂度为O(N^2)
思路二:我们使用三段逆置,我们先让前n-k个逆置一下,然后再把后k个逆置一下,最后整体逆置。

代码如下:
void reverse(int*a,int left,int raght)
{while(left < raght){int temp = a[left];a[left] = a[raght];a[raght] = temp;++left;--raght;}
}
void rotate(int* nums, int numsSize, int k)
{k %= numsSize;reverse(nums,0,numsSize-k-1);reverse(nums,numsSize-k,numsSize-1);reverse(nums,0,numsSize-1);
}时间复杂度为O(N),我们也可以使用memcpy
总结
时间复杂度是衡量算法执行效率的重要指标,它表示算法随输入数据规模增长时执行时间的变化趋势。优化时间复杂度可以节省计算资源、提高系统性能、满足实时性要求,并提升用户体验。在设计算法时,应充分考虑时间复杂度的优化,以实现高效、稳定的性能表现。
相关文章:

算法的时间复杂度(详解)
前言: 算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为 输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果 一、算法效率 1.1 如何衡量一个算法的好坏 如何衡…...

Flutter 中的 NestedScrollViewViewport 小部件:全面指南
Flutter 中的 NestedScrollViewViewport 小部件:全面指南 Flutter 是一个功能丰富的 UI 工具集,它提供了多种布局和控件来帮助开发者构建美观且功能强大的应用。在 Flutter 的滚动控件中,NestedScrollView 是一个特别的存在,它允…...
断开自定义模块与自定义库的链接
断开自定义模块与自定义库的链接 1、断开模块与库的链接 1、断开模块与库的链接 如果摸个库文件添加到模型中,无法“Disable Link”时,可以使用save_system命令进行断开到模型中用户定义的库模块的链接; 参考链接: 传送门 save…...

粉丝问,有没有UI的统计页面,安排!
移动应用的数据统计页面具有以下几个重要作用: 监控业务指标:数据统计页面可以帮助用户监控关键业务指标和数据,例如用户活跃度、销售额、转化率等。通过实时更新和可视化呈现数据,用户可以及时了解业务的整体状况和趋势。分析用…...

Nginx R31 doc-17-debugging 调试
前言 大家好,我是老马。很高兴遇到你。 我们为 java 开发者实现了 java 版本的 nginx https://github.com/houbb/nginx4j 如果你想知道 servlet 如何处理的,可以参考我的另一个项目: 手写从零实现简易版 tomcat minicat 手写 nginx 系列 …...

python -【一】基础语法
python 基础语法 一. 基础数据类型 常用的 6 种数据类型 类型描述说明数字(Number)int,float,complex(复数),bool复数:4 3j,j 表示复数字符串(String)文本࿱…...
数据结构 | 详解二叉树——堆与堆排序
🥝堆 堆总是一棵完全二叉树。 大堆:父节点总是大于子节点。 小堆:父节点总是小于子节点。 注意:1.同一个节点下的两个子节点并无要求先后顺序。 2.堆可以是无序的。 🍉堆的实现 🌴深度剖析 1.父节点和子…...

vb.net,C#强制结束进程,“优雅”的退出方式
在VB.NET中,Application.Exit()和Environment.Exit(0)都用于结束程序,但它们的使用场景和背后的逻辑略有不同。 **Application.Exit()**: Application.Exit()通常用于Windows Forms应用程序中。当调用Application.Exit()时,它会触…...

牛客热题:数据流中的中位数
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:数据流中的中位数题目链接方法一…...
JavaScript-JavaWeb
目录 什么是JavaScript? js引入方式 js基础语法 书写语法 变量 数据据类型 运算符 类型转换 流程语句 js函数 js对象 1.Array 2.String 3.JSON js事件监听 什么是JavaScript? ● JavaScript(简称:JS)是一门跨平台、面向对象的脚本语言。是用来控制网页行为的,它能…...

vue组件通讯$parent和$children获取单签组件的⽗组件和当前组件的⼦组件的例子
在 Vue 中,$parent 和 $children 是实例属性,允许你访问组件的父组件和子组件。但是,请注意,这些属性主要用于在开发过程中进行调试和临时访问,并不推荐在正常的组件通信中使用,因为它们破坏了组件的封装性…...

Util和utils
Util FieldStats 这段代码定义了一个名为FieldStats的Java类,位于com.cqupt.software_1.Util包中。它使用了lombok库的Data和AllArgsConstructor注解,这些注解帮助生成了getter、setter、toString等方法,以及包含所有参数的构造函数。类中有…...
拷贝构造、移动构造、拷贝赋值、移动赋值
最近在学习C的拷贝构造函数时发现一个问题:在函数中返回局部的类对象时,并没有调用拷贝构造函数。针对这个问题,查阅了一些资料,这里记录整理一下。 调用拷贝构造函数的三种情况: ① 用一个类去初始化另一个对象时&a…...

Python3 笔记:math模块
要使用 math 函数必须先导入math模块 语法:import math Python math 模块提供了许多对浮点数的数学运算函数。 math 模块下的函数,返回值均为浮点数,除非另有明确说明。 如果需要计算复数,需使用 cmath 模块中的同名函数。 m…...

python -【四】函数
函数 一、函数的基础 函数:是组织好的,可以重复使用的,用来实现特定功能的代码段 语法 def 函数名(入参): return 出参 # 定义函数 def out_hello():print(hello ~~~)# 调用/使用/执行函数 out_hello()练习题 自定义一个函数,…...

力扣 5. 最长回文子串 python AC
动态规划 class Solution:def longestPalindrome(self, s):size len(s)maxl 1start 0dp [[False] * size for _ in range(size)]for i in range(size):dp[i][i] Truefor L in range(2, size 1):for i in range(size):j L i - 1if j > size:breakif s[i] s[j]:if L…...
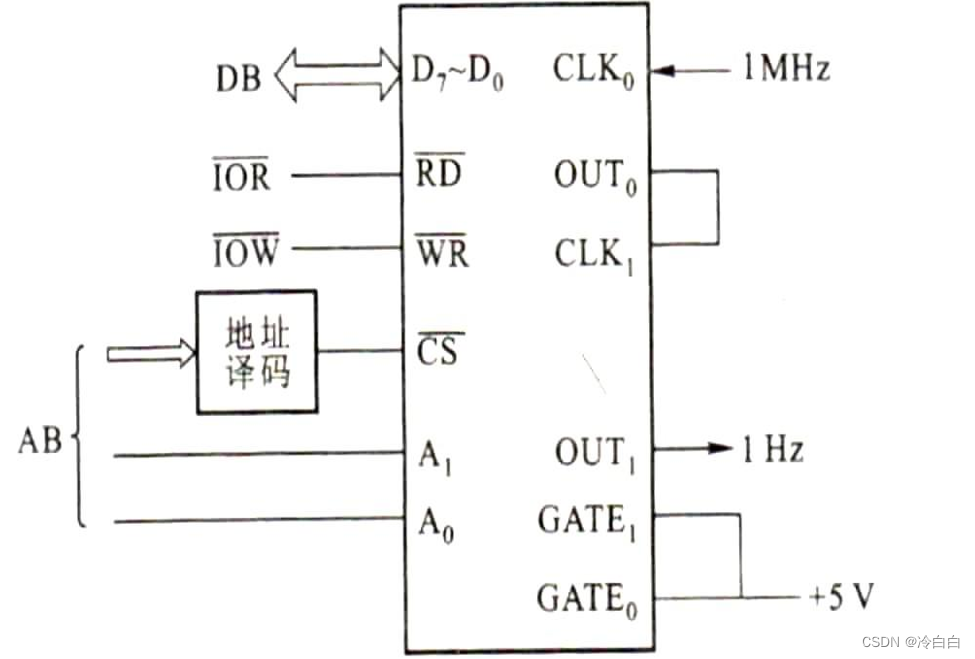
【微机原理及接口技术】可编程计数器/定时器8253
【微机原理及接口技术】可编程计数器/定时器8253 文章目录 【微机原理及接口技术】可编程计数器/定时器8253前言一、8253的内部结构和引脚二、8253的工作方式三、8253的编程总结 前言 本篇文章就8253芯片展开,详细介绍8253的内部结构和引脚,8253的工作方…...

23种设计模式之一— — — —装饰模式详细介绍与讲解
装饰模式详细讲解 一、定义二、装饰模式结构核心思想模式角色模式的UML类图应用场景模式优点模式缺点 实例演示图示代码演示运行结果 一、定义 装饰模式(别名:包装器) 装饰模式(Decorator Pattern)是结构型的设计模式…...

2024年2月28日 星期三
2024年2月28日 星期三 农历正月十九 1. 住建部:各城市要做好今明两年住房发展计划,防止市场大起大落。 2. 政协委员赵长龙建议:增加元旦、端午、中秋高速免费,周六日半价。 3. 人民法院案例库开始对社会开放,与中国…...

Java中的super关键字详解
在Java编程中,super关键字是一个非常重要的概念,尤其是在继承和多态的场景中。理解super关键字的使用方法和其背后的机制,对于掌握面向对象编程(OOP)的基本概念至关重要。本篇博客将详细讲解super关键字的各种用法及其…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
