「清新题精讲」Skiers
更好的阅读体验
Skiers
Description
给定 n n n 个点的有向无环平面图,求最少多少条从 1 1 1 到 n n n 的路径能覆盖原图的所有边?
1 ≤ n ≤ 5 × 1 0 3 1\le n\le 5\times10^3 1≤n≤5×103
Solution
考虑从 1 1 1 到 n n n 的路径其实是边的链覆盖,那么最小链覆盖即为求解的答案。通过 Dilworth 定理可知,最小链覆盖等于最大反链,从而问题转化为求最大反链(两两无法到达的边的集合)。
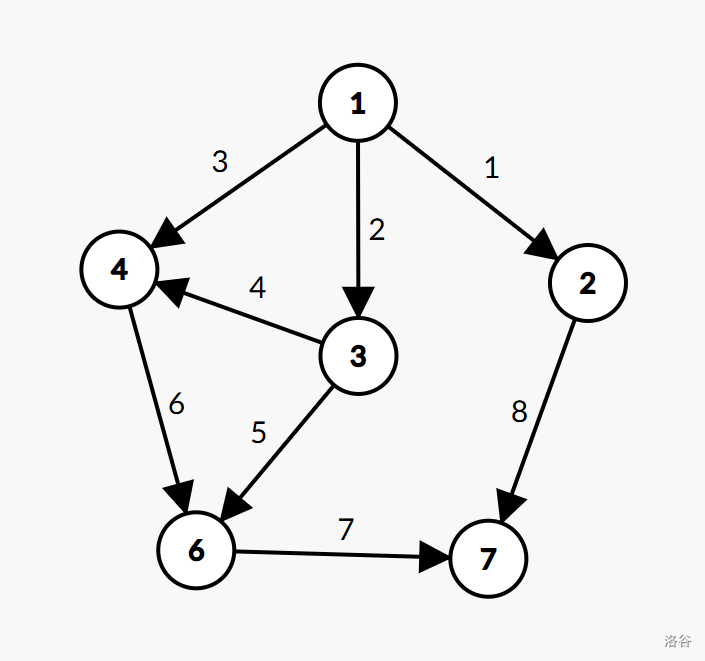
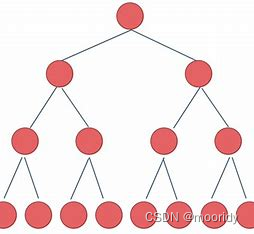
例如:图示的有向无环平面图, 1 1 1 号点为起点, 7 7 7 号点为汇点。最大反链是 3 , 4 , 5 , 8 3,4,5,8 3,4,5,8 边构成的集合(注意集合不唯一),不难发现原图的答案就是 4 4 4。
考虑如何求解最大反链,可以将平面图转化为对偶图,则最大反链即为对偶图的最长路。
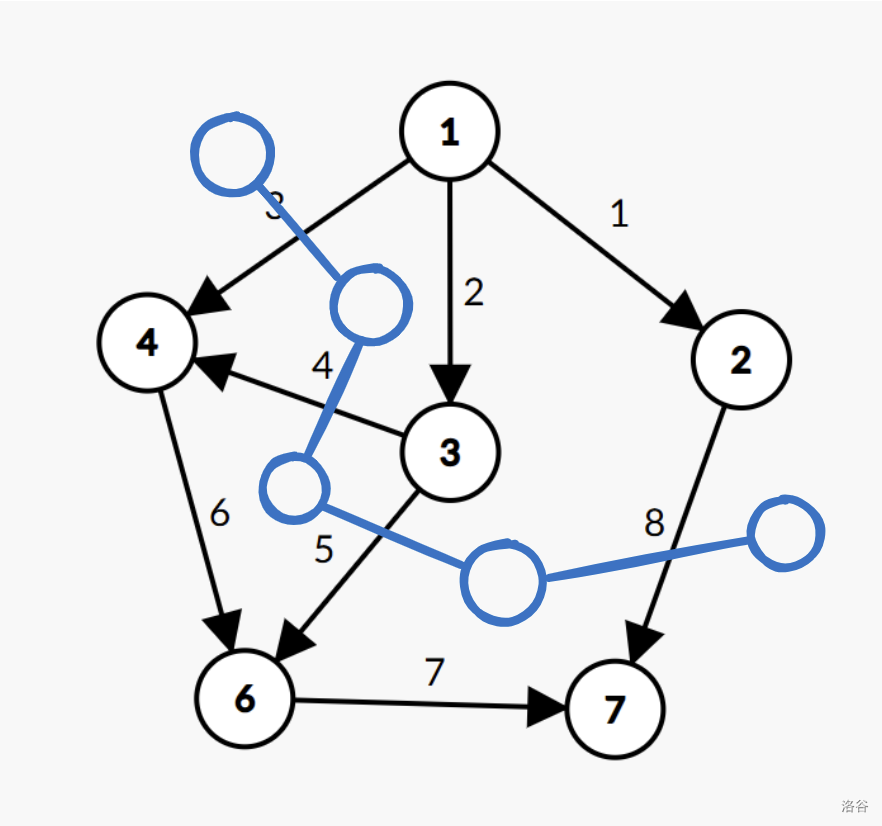
如图,给出了原图的对偶图的最长路,注意这里多开了虚拟起点和汇点。
那么,怎么求最长路呢,这里给出一种简单又迅速的做法,从起点开始 DFS,如果遍历到 1 1 1 个点之前已经遍历过了,那么说明多出了一条对偶图的边。
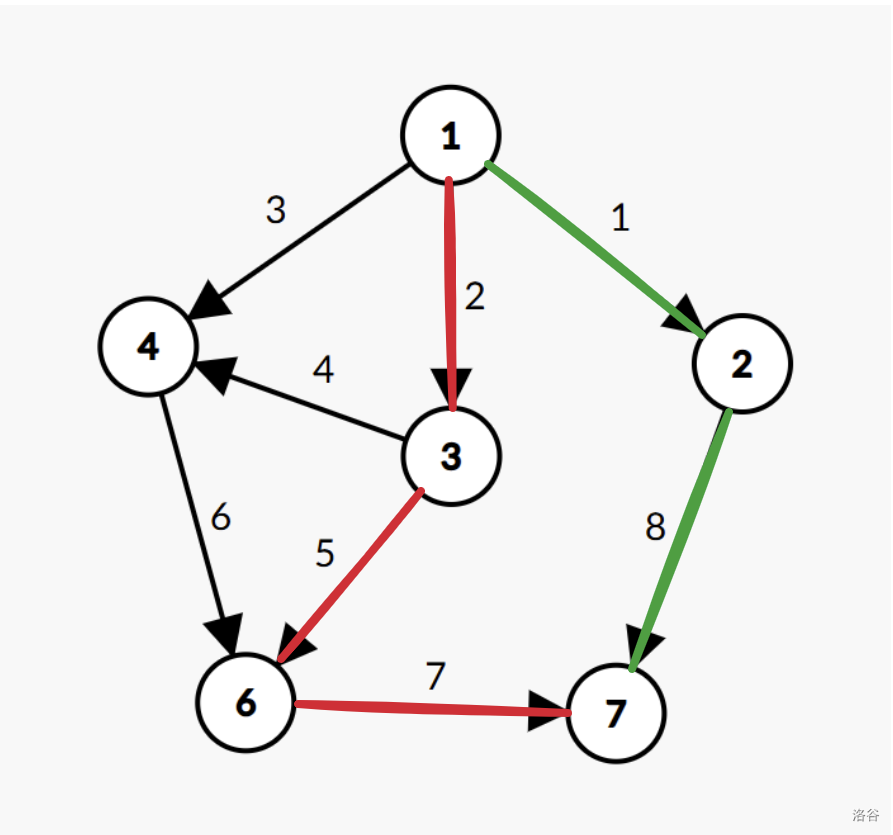
若绿色路径为当前 DFS 的路径,红色为之前 DFS 的路径,此时发现到达了一个已经经过的点,则从该点开始将红色的边筛出来,直到绿色节点经过过的点,即 1 1 1 号节点。用红色边最长路 + 1 +1 +1 再去更新绿色边的最长路即可。
Code
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int N = 5e3 + 10, M = 3 * N;int n;
int h[N], e[M], ne[M], idx;
int st[N], dp[M];
PII lst[N];void add(int a, int b) {e[idx] = b, ne[idx] = h[a], dp[idx] = 1, h[a] = idx ++;
}
void dfs(int u) {st[u] = 1;for (int i = h[u]; ~i; i = ne[i]) {int v = e[i];if (st[v] == 0) lst[v] = {u, i}, dfs(v);else {int res = 0, tmp = u;while (st[v] == -1) res = max(res, dp[lst[v].se] + 1), v = lst[v].fi;dp[i] = res;while (tmp != v) dp[lst[tmp].se] = res, tmp = lst[tmp].fi;lst[e[i]] = {u, i};}}st[u] = -1;
}signed main() {cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> n;memset(h, -1, sizeof h);int k, x;for (int i = 1; i < n; i ++) {cin >> k;for (int j = 1; j <= k; j ++)cin >> x, add(i, x);}dfs(1);int res = 0;for (int i = 0; i < idx; i ++)res = max(res, dp[i]);cout << res << endl;return 0;
}
相关文章:

「清新题精讲」Skiers
更好的阅读体验 Skiers Description 给定 n n n 个点的有向无环平面图,求最少多少条从 1 1 1 到 n n n 的路径能覆盖原图的所有边? 1 ≤ n ≤ 5 1 0 3 1\le n\le 5\times10^3 1≤n≤5103 Solution 考虑从 1 1 1 到 n n n 的路径其实是边的链覆…...
-基于transformer的英文到中文翻译模型)
Transformer详解(8)-基于transformer的英文到中文翻译模型
1、数据使用TED,数据清洗 WIT是“转录和翻译演讲网络清单”的缩写,是 TED 演讲多语言转录的现成版本,可用于研究目的。 2、英文中文翻译模型搭建 3、模型训练 4、模型推理...

算法的时间复杂度(详解)
前言: 算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为 输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果 一、算法效率 1.1 如何衡量一个算法的好坏 如何衡…...

Flutter 中的 NestedScrollViewViewport 小部件:全面指南
Flutter 中的 NestedScrollViewViewport 小部件:全面指南 Flutter 是一个功能丰富的 UI 工具集,它提供了多种布局和控件来帮助开发者构建美观且功能强大的应用。在 Flutter 的滚动控件中,NestedScrollView 是一个特别的存在,它允…...
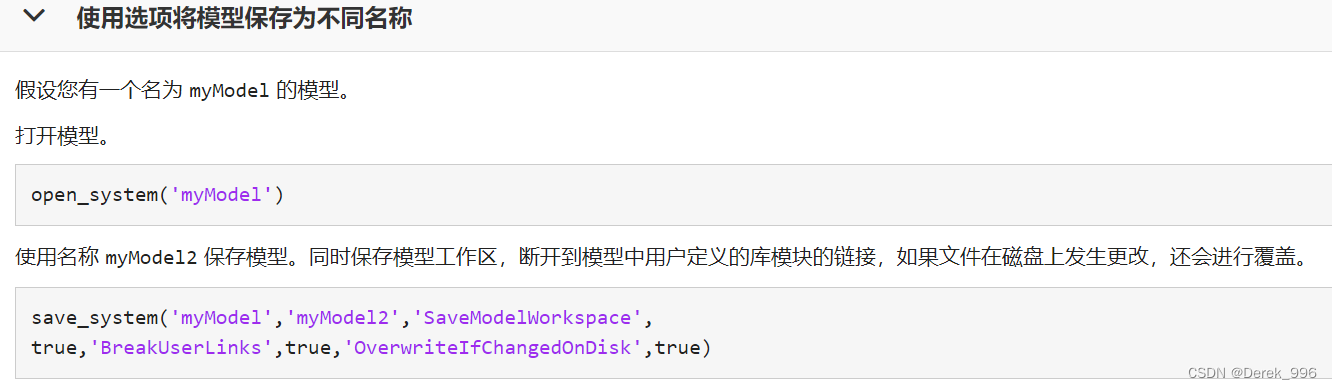
断开自定义模块与自定义库的链接
断开自定义模块与自定义库的链接 1、断开模块与库的链接 1、断开模块与库的链接 如果摸个库文件添加到模型中,无法“Disable Link”时,可以使用save_system命令进行断开到模型中用户定义的库模块的链接; 参考链接: 传送门 save…...

粉丝问,有没有UI的统计页面,安排!
移动应用的数据统计页面具有以下几个重要作用: 监控业务指标:数据统计页面可以帮助用户监控关键业务指标和数据,例如用户活跃度、销售额、转化率等。通过实时更新和可视化呈现数据,用户可以及时了解业务的整体状况和趋势。分析用…...

Nginx R31 doc-17-debugging 调试
前言 大家好,我是老马。很高兴遇到你。 我们为 java 开发者实现了 java 版本的 nginx https://github.com/houbb/nginx4j 如果你想知道 servlet 如何处理的,可以参考我的另一个项目: 手写从零实现简易版 tomcat minicat 手写 nginx 系列 …...

python -【一】基础语法
python 基础语法 一. 基础数据类型 常用的 6 种数据类型 类型描述说明数字(Number)int,float,complex(复数),bool复数:4 3j,j 表示复数字符串(String)文本࿱…...
数据结构 | 详解二叉树——堆与堆排序
🥝堆 堆总是一棵完全二叉树。 大堆:父节点总是大于子节点。 小堆:父节点总是小于子节点。 注意:1.同一个节点下的两个子节点并无要求先后顺序。 2.堆可以是无序的。 🍉堆的实现 🌴深度剖析 1.父节点和子…...

vb.net,C#强制结束进程,“优雅”的退出方式
在VB.NET中,Application.Exit()和Environment.Exit(0)都用于结束程序,但它们的使用场景和背后的逻辑略有不同。 **Application.Exit()**: Application.Exit()通常用于Windows Forms应用程序中。当调用Application.Exit()时,它会触…...

牛客热题:数据流中的中位数
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:数据流中的中位数题目链接方法一…...
JavaScript-JavaWeb
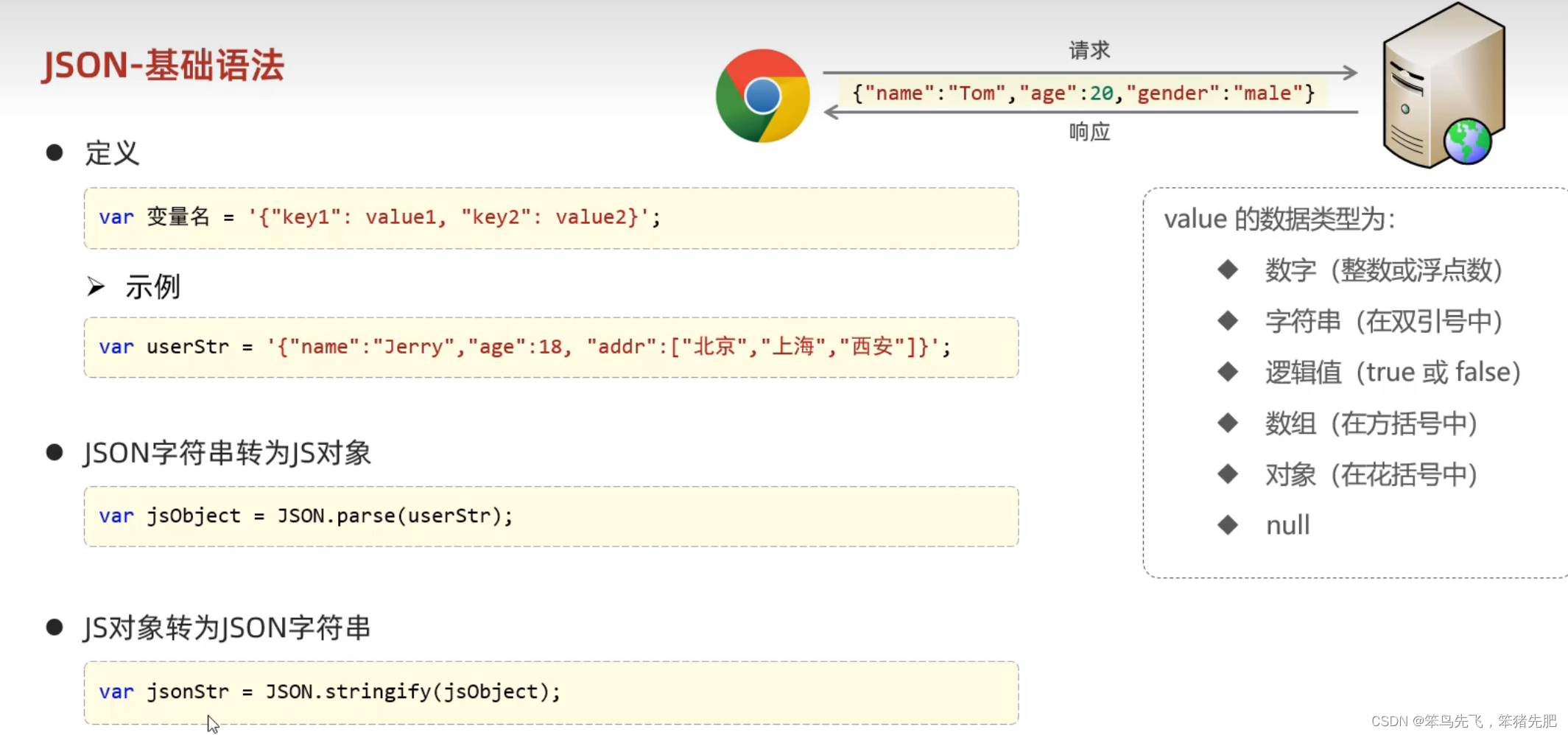
目录 什么是JavaScript? js引入方式 js基础语法 书写语法 变量 数据据类型 运算符 类型转换 流程语句 js函数 js对象 1.Array 2.String 3.JSON js事件监听 什么是JavaScript? ● JavaScript(简称:JS)是一门跨平台、面向对象的脚本语言。是用来控制网页行为的,它能…...

vue组件通讯$parent和$children获取单签组件的⽗组件和当前组件的⼦组件的例子
在 Vue 中,$parent 和 $children 是实例属性,允许你访问组件的父组件和子组件。但是,请注意,这些属性主要用于在开发过程中进行调试和临时访问,并不推荐在正常的组件通信中使用,因为它们破坏了组件的封装性…...

Util和utils
Util FieldStats 这段代码定义了一个名为FieldStats的Java类,位于com.cqupt.software_1.Util包中。它使用了lombok库的Data和AllArgsConstructor注解,这些注解帮助生成了getter、setter、toString等方法,以及包含所有参数的构造函数。类中有…...
拷贝构造、移动构造、拷贝赋值、移动赋值
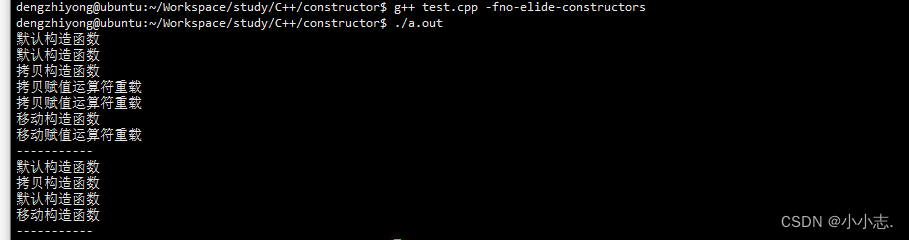
最近在学习C的拷贝构造函数时发现一个问题:在函数中返回局部的类对象时,并没有调用拷贝构造函数。针对这个问题,查阅了一些资料,这里记录整理一下。 调用拷贝构造函数的三种情况: ① 用一个类去初始化另一个对象时&a…...

Python3 笔记:math模块
要使用 math 函数必须先导入math模块 语法:import math Python math 模块提供了许多对浮点数的数学运算函数。 math 模块下的函数,返回值均为浮点数,除非另有明确说明。 如果需要计算复数,需使用 cmath 模块中的同名函数。 m…...

python -【四】函数
函数 一、函数的基础 函数:是组织好的,可以重复使用的,用来实现特定功能的代码段 语法 def 函数名(入参): return 出参 # 定义函数 def out_hello():print(hello ~~~)# 调用/使用/执行函数 out_hello()练习题 自定义一个函数,…...

力扣 5. 最长回文子串 python AC
动态规划 class Solution:def longestPalindrome(self, s):size len(s)maxl 1start 0dp [[False] * size for _ in range(size)]for i in range(size):dp[i][i] Truefor L in range(2, size 1):for i in range(size):j L i - 1if j > size:breakif s[i] s[j]:if L…...
【微机原理及接口技术】可编程计数器/定时器8253
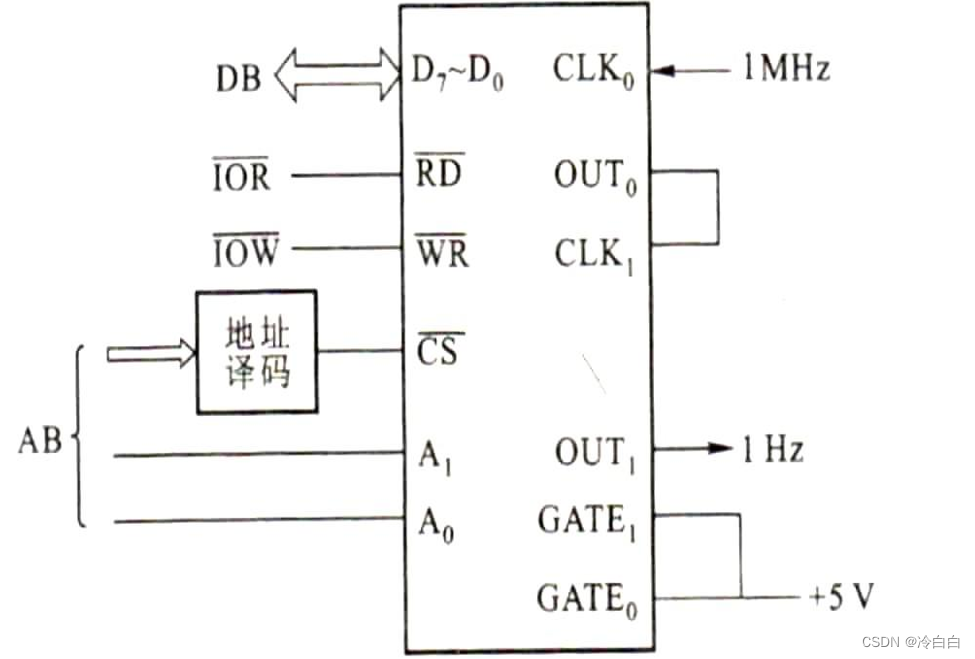
【微机原理及接口技术】可编程计数器/定时器8253 文章目录 【微机原理及接口技术】可编程计数器/定时器8253前言一、8253的内部结构和引脚二、8253的工作方式三、8253的编程总结 前言 本篇文章就8253芯片展开,详细介绍8253的内部结构和引脚,8253的工作方…...

23种设计模式之一— — — —装饰模式详细介绍与讲解
装饰模式详细讲解 一、定义二、装饰模式结构核心思想模式角色模式的UML类图应用场景模式优点模式缺点 实例演示图示代码演示运行结果 一、定义 装饰模式(别名:包装器) 装饰模式(Decorator Pattern)是结构型的设计模式…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
