[双指针] --- 快乐数 盛最多水的容器
Welcome to 9ilk's Code World

(๑•́ ₃ •̀๑) 个人主页: 9ilk
(๑•́ ₃ •̀๑) 文章专栏: 算法Journey
本篇博客我们分享一下双指针算法中的快慢指针以及对撞双指针,下面我们开始今天的学习吧~
🏠 快乐数
📒 题目解析
题目链接:202. 快乐数 - 力扣(LeetCode)
题目内容:
对于这道题,题中告诉了我们快乐数的定义,也就是说9对于一个正整数经过变换会进入两种循环:1.一种是一直循环12.另一种是不同数的循环
📒 算法原理
思路1 找规律
这个思路本人按照以往学数学的规律,发现不满足快乐数的会陷入4-16-37-58-89-145-42-20的循环当中

因此我们的思路是申请一块数组空间,当某个正整数变化到这个数组中的某个数时,说明不是快乐数;反之,一直变化都没出现这里面的数,变化到1停止,说明就是快乐数。
参考代码
class Solution
{
public:int squre(int n){int sum = 0 ;while(n > 0){sum += ((n%10)*(n%10));n /= 10;}return sum;}bool find(vector<int>& v1,int x){for(int i = 0 ; i < v1.size();i++){if(v1[i] == x)return true;}return false;}bool isHappy(int n) {if(n == 1)return true;vector<int> v1= {4,16,37,58,89,145,42,20};int sum = n;while(sum != 1){sum = squre(sum);if(find(v1,sum))return false;elsecontinue; }return true;}
};思路2 快慢指针
思路1属于投机取巧的做法,猜到就是赚到,万一猜不到呢?
我们由题目可知,这个正整数只有两种变化情况,有的朋友可能会想是否有可能不会进入循环一直变成不同的数呢?答案是不可能 !
证明过程:
1.鸽巢(抽屉)原理:如果有n个巢,n+1只鸽子,那么至少有一个巢的鸽数大于1.
2.对于这道题而言最大为21亿多( 2147483647),也就是最多有10个位,假设每一位都是9,即9999999999,那么经过一次变换就是9*9*10 = 810
3.int范围内每个正整数经过一次变化在[0,810]这个闭区间内,那么假设存在某个数经过810次变换后都是不同的数,但再变一次这个数一定是之前变换过程中的一个数,类比来看,这个闭区间就相当于"鸽巢",因此一定会进入循环!
既然只有两种情况,我们看到两种环是否感到熟悉,我们在解决链表是否带环问题,常用的解决方法就是快慢指针
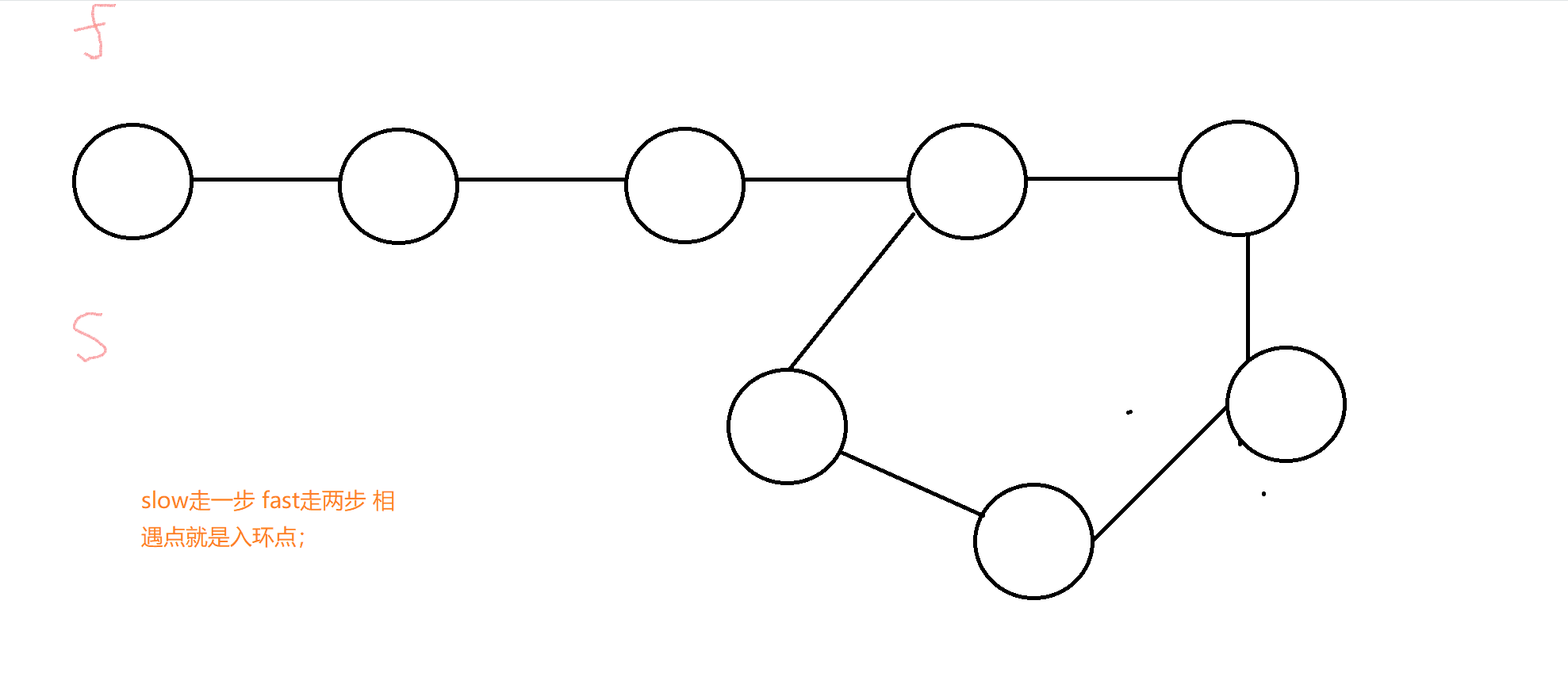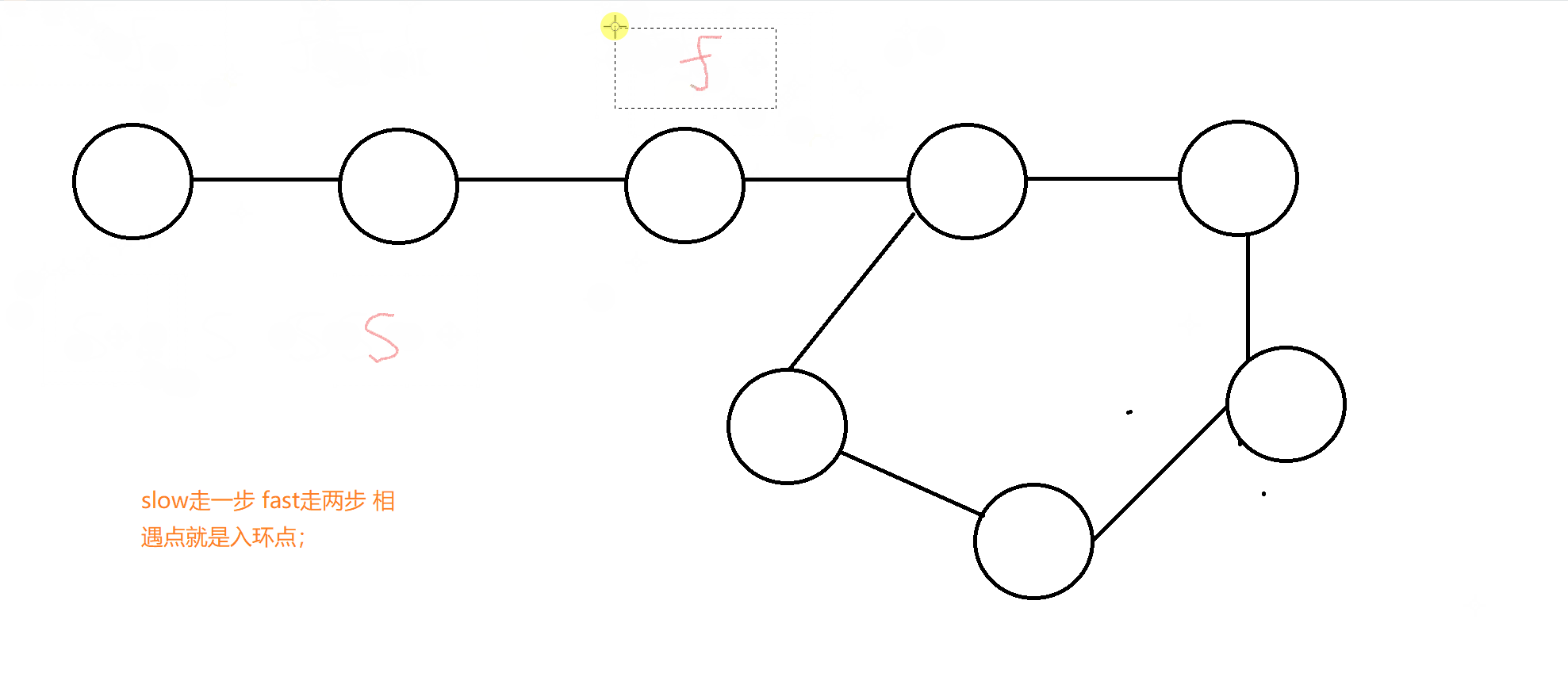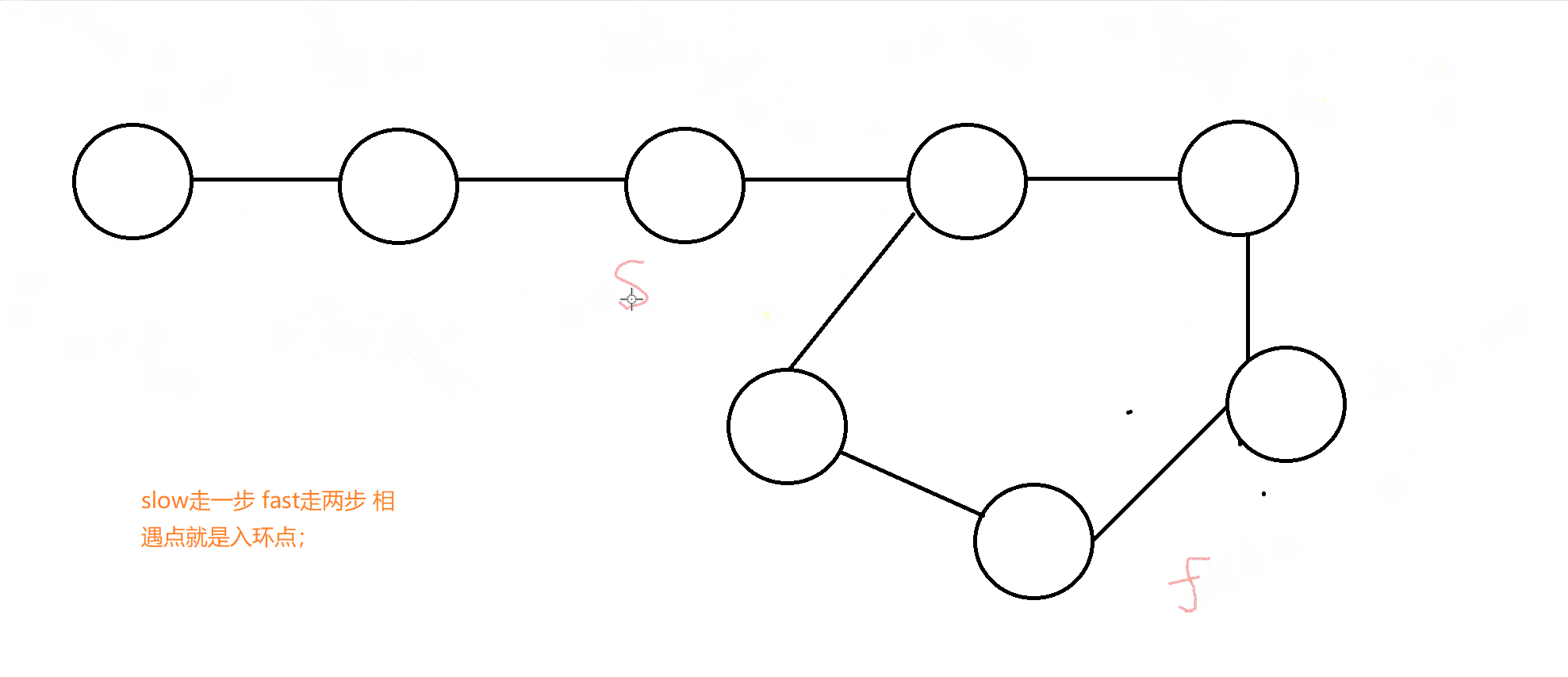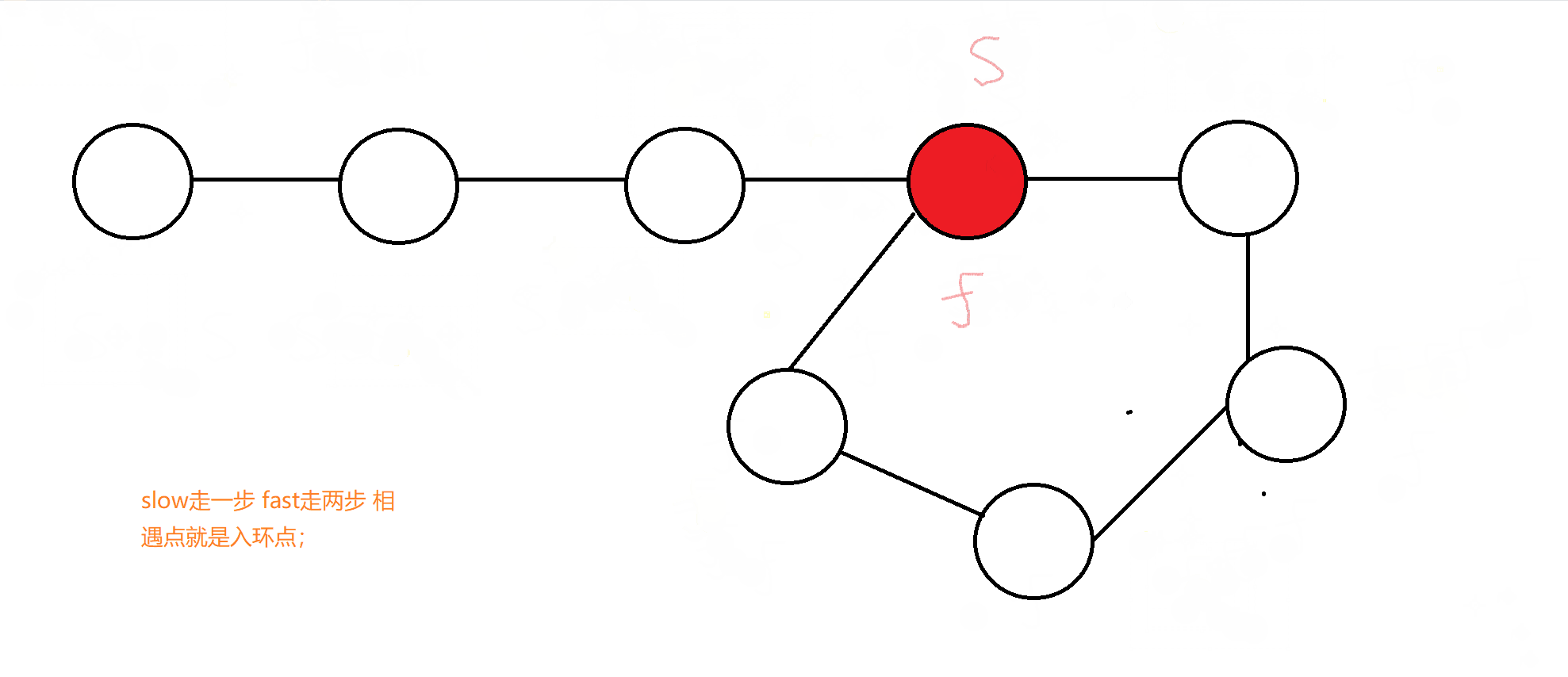
这里我们要打破固有思维,我们要理解的是快慢指针的应用场景,在这里slow走一步相当于这个正整数变化一次,fast走两步,相当于这个正整数变化两次
总结快慢指针思路:slow变化一次,fast变化两次,通过判断他们相遇时(变化成的数相等时),这个数是否变化为1,为1则说明是快乐数;反之不是.
参考代码
class Solution {
public:int squre(int x){int sum = 0;while(x > 0){sum += ((x%10)*(x%10));x /= 10;} return sum;}bool isHappy(int n){int slow = squre(n);int fast = squre(squre(n));while(slow != fast){slow = squre(slow);fast = squre(squre(fast));}if(slow == 1){return true;}return false;}};🏠 盛最多水的容器
📒 题目解析
题目链接:11. 盛最多水的容器 - 力扣(LeetCode)
题目内容:
这道题目简单来说就是让我们确定横坐标差值m以及纵坐标n,使得m*n最大
📒 算法原理
思路1 暴力求解
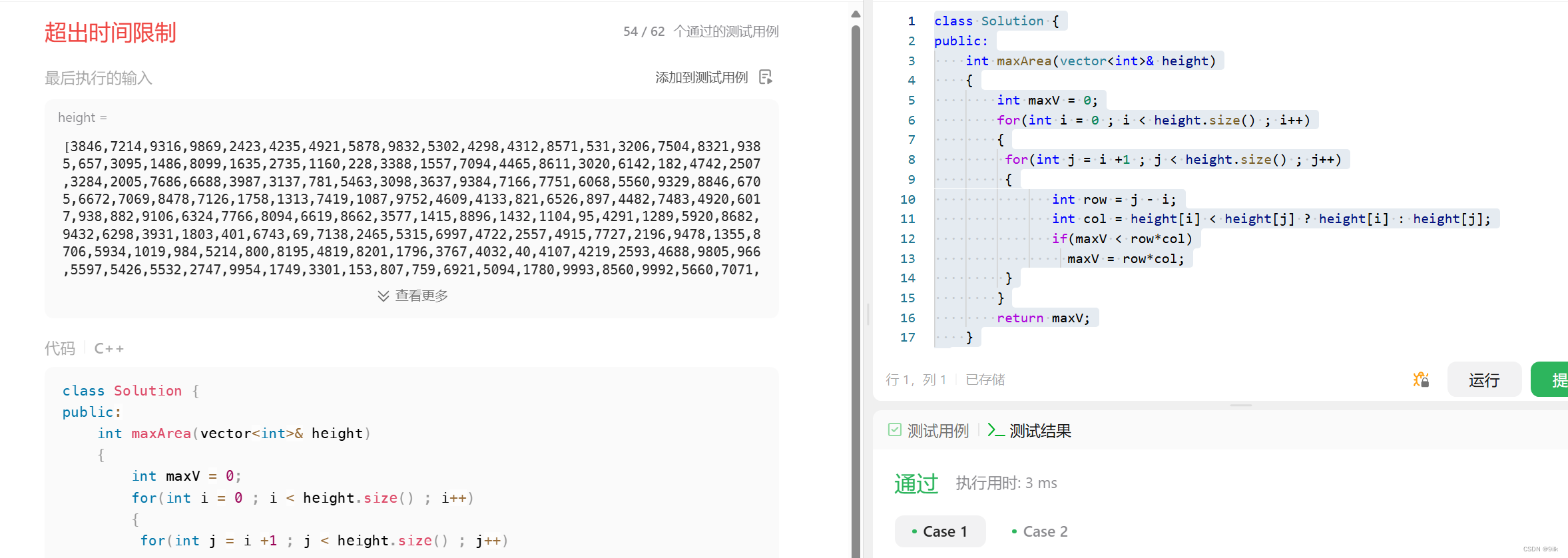
对于这道题我第一时间能想到的就是暴力求解套两个循环,定义一个max变量,不断比较更新max
class Solution {
public:int maxArea(vector<int>& height){int maxV = 0;for(int i = 0 ; i < height.size() ; i++){for(int j = i +1 ; j < height.size() ; j++){int row = j - i;int col = height[i] < height[j] ? height[i] : height[j];if(maxV < row*col)maxV = row*col;}}return maxV;}
};但题目不给我们过O(N^2)的解法,需要另寻他路
思路2 对撞指针
发现规律:
假设在【6,2,3,4】这个区间,我们设横坐标值为m,纵坐标的值为n,则固定住4,4左边的数分别与4求体积我们会发现这样的一个规律:
结论:当区间左右端点值较小的值固定住后,不断逼近过程中,V一定是一定减小的,那么左右端点值形成的V就是这段区间中最大的!!
发现完这个规律,我们就可以避免了很多不必要情况的枚举,直捣黄龙取“最大”。
对撞指针:所谓对撞指针就是定义一个left指针和一个指针,分别指向容器的左右端,left和right分别向中间逼近,当left > right或 left == right时,停止遍历。
结合我们发现的规律以及对撞指针的原理,我们的代码思路就是left和right分别向中间逼近,比较left和right 位置对应位置的较小值固定 left / right,求出左右端点值对应的v;由发现的规律知,此时的v就是这个对应左右边界最大的v;接着移动left / right,继续下一个左右区间...直到left 和 right 相遇。
参考代码
class Solution {
public:int maxArea(vector<int>& height) {int left = 0;int right = height.size() - 1;vector<int> v1;while(left < right){int v = (right-left)*(height[left] < height[right] ? height[left] :height[right]);v1.push_back(v);cout << v << " left :"<<left << "right: "<< right << endl;if(height[left] < height[right]){left++;}else if(height[left] > height[right]){right--;}else{left++;}}int maxV = 0;for(int i = 0 ; i < v1.size();i++){if(v1[i]>maxV)maxV = v1[i];}return maxV;}
};总结:本篇博客我们介绍了双指针算法中的快慢指针和对撞指针;快慢指针常用于解决“带环”问题,对撞指针需要我们先发现规律确定好对撞停止条件以及对撞指针更新的条件,一般适用于排除区间或查找某种条件是否成立的场景
相关文章:

[双指针] --- 快乐数 盛最多水的容器
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏: 算法Journey 本篇博客我们分享一下双指针算法中的快慢指针以及对撞双指针,下面我们开始今天的学习吧~ 🏠 快乐数 📒 题…...
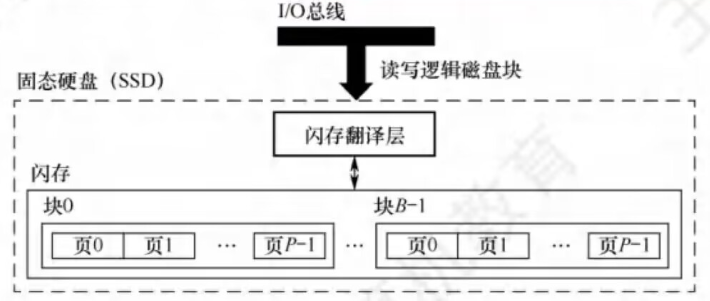
操作系统 - 输入/输出(I/O)管理
输入/输出(I/O)管理 考纲内容 I/O管理基础 设备:设备的基本概念,设备的分类,I/O接口 I/O控制方式:轮询方式,中断方式,DMA方式 I/O软件层次结构:中断处理程序,驱动程序,…...
| 二叉树 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树)
代码随想录算法训练营第22天(py)| 二叉树 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
669. 修剪二叉搜索树 力扣链接 给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>L) 思路 如果当前节点元素小于low,递归右子树,返回符合条件的头节点 如果当前节点元…...

使用C语言实现学生信息管理系统
前言 在我们实现学生信息管理系统的过程中,我们几乎会使用到C语言最常用最重要的知识,对于刚学习完C语言的同学来说是一次很好的巩固机会,其中还牵扯到数据结果中链表的插入和删除内容。 实现学生信息管理系统 文件的创建与使用 对于要实现…...

上下文视觉提示实现zero-shot分割检测及多visual-prompt改造
文章目录 一、Closed-Set VS Open-set二、DINOv2.1 论文和代码2.2 内容2.3 安装部署2.4 使用效果 三、多visual prompt 改造3.1 获取示例图mask3.2 修改函数参数3.3 推理代码3.4 效果的提升! 四、总结 本文主要介绍visual prompt模型DINOv,该模型可输入八…...

WebGL学习(一)渲染关系
学习webgl 开发理解渲染关系是必须的,也非常重要,很多人忽视了这个过程。 我这里先简单写一下,后面尽量用通俗易懂的方式,举例讲解。 WebGL,全称Web Graphics Library,是一种在网页上渲染3D图形的技术。它…...

人生建议:向猫学习
心安理得地被爱 猫从不担心自己不配得到爱,也正是这幅理所应当、宠辱不惊的样子,让人欲罢不能。或许 当你相信自己值得世界上最好的爱时,你就会拥有。 多晒太阳多睡觉 猫喜欢睡觉,尤其喜欢躺阳光好的地方。阳光和睡眠,…...

软件架构设计属性之三:结构性属性浅析
文章目录 引言一、结构性属性的定义二、结构性属性的关键要素1. 组件化2. 模块化3. 层次化4. 接口定义5. 数据流6. 依赖管理 三、结构性属性的设计原则1. 高内聚低耦合2. 松耦合3. 清晰的接口4. 可维护性5. 可扩展性 四、结构性属性的实现策略1. 组件划分2. 模块化设计3. 接口设…...
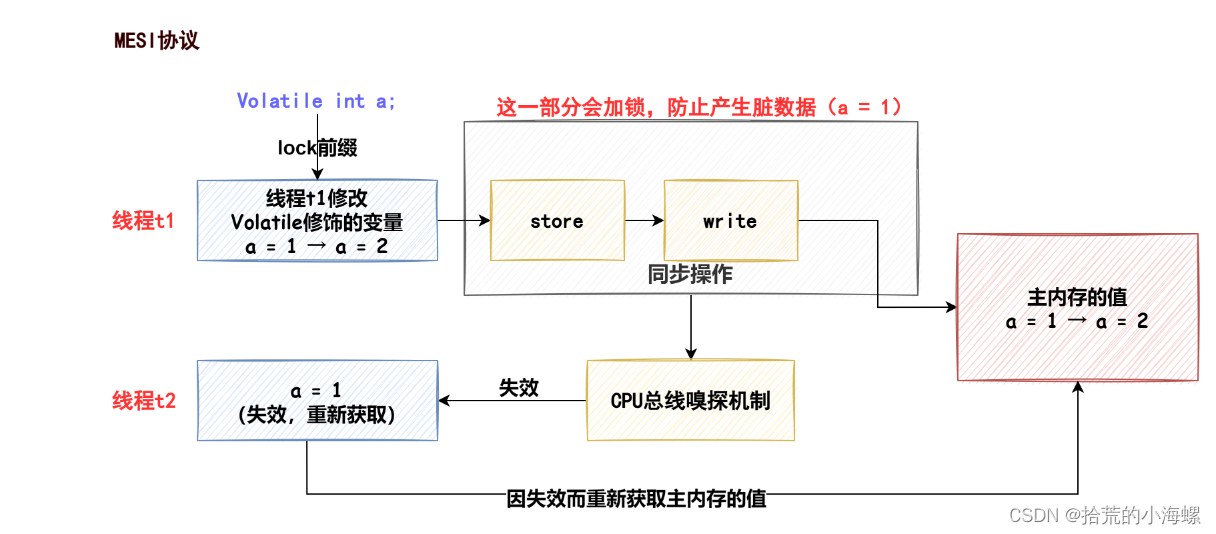
JAVA:多线程常见的面试题和答案
请关注微信公众号:拾荒的小海螺 博客地址:http://lsk-ww.cn/ 1、并发编程三要素? 原 子 性 原子性指的是一个或者多个操作,要么全部执行并且在执行的过程中不被其他操作打断,要么就全部都不执行。可 见 性 可见性指多…...

短信平台-平台群发短信
时代的进步带来了我们生活的便利,而其中最受欢迎和广泛应用的方式之一就是通过短信传递信息。在这个飞速发展的数字时代,我们需要一个高效、可靠的短信平台来满足不断增长的通讯需求。而今天,我要向大家推荐的正是这样一款卓越的短信平台——…...

C++:类和对象
一、前言 C是面向对象的语言,本文将通过上、中、下三大部分,带你深入了解类与对象。 目录 一、前言 二、部分:上 1.面向过程和面向对象初步认识 2.类的引入 3.类的定义 4.类的访问限定符及封装 5.类的作用域 6.类的实例化 7.类的…...

JavaScript条件语句与逻辑判断:解锁代码逻辑的奥秘【含代码示例】
JavaScript条件语句与逻辑判断:解锁代码逻辑的奥秘【含代码示例】 基本概念与作用if...else:决策的基础switch:多路分支的能手逻辑运算符:连接逻辑的纽带三元运算符:简洁的力量 功能使用思路与技巧短路求值优化防止swi…...

sparksql自定义函数
前言 Spark SQL UDF(也称为用户定义函数)是Spark SQL&DataFrame最有用的功能,它扩展了Spark内置功能。在本文中,我将解释什么是UDF?为什么我们需要它,以及如何使用Java、Scala示例在DataFrame和SQL上创建和使用它。 注意:UDF是最昂贵的操作,因此只有在必要时才使用…...

新人开发新系统,旧人维护旧系统
通常来说旧系统存在一些难以解决的问题,软件架构及逻辑实现可能会有一定的缺陷和复杂度,甚至有些烂系统可以称为”焦油坑“,意思是出现问题难以分析解决,谁来谁陷进去。因此,如果同时存在新系统(可能正在开…...

鸿蒙应用模型:【Stage模型开发】概述
Stage模型开发概述 基本概念 下图展示了Stage模型中的基本概念。 图1 Stage模型概念图 [AbilityStage] 每个Entry类型或者Feature类型的HAP在运行期都有一个AbilityStage类实例,当HAP中的代码首次被加载到进程中的时候,系统会先创建AbilityStage实例…...

java使用jdbcTemplatep批量插入数据
JdbcTemplate 是 Spring 框架中提供的一个简化 JDBC 操作的工具类,它封装了 JDBC 的核心功能,使得开发者能够更方便、简洁地进行数据库操作。 下面是一个使用 JdbcTemplate 进行批量插入的示例: import org.springframework.jdbc.core.Batch…...
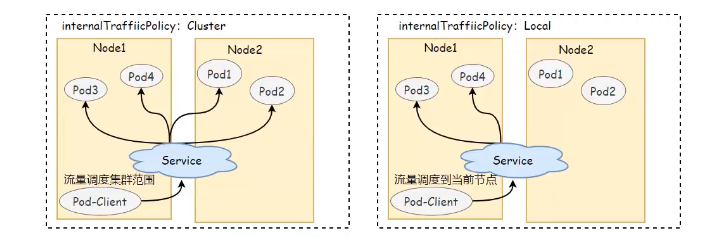
K8s service 进阶
文章目录 K8s service 进阶Service 工作逻辑Service 具体实现Service 资源类型ClusterIPNodePortLoadBalancerExternalName Service 与 EndpointEndpoint 与 容器探针自定义Endpoint Service 相关字段sessionAffinityexternalTrafficPolicyinternalTrafficPolicypublishNotRead…...

CompletableFuture详细讲解
目录 一、基本概念 1.1 异步编程 1.2 CompletableFuture简介 二、创建和完成CompletableFuture 2.1 创建CompletableFuture对象 2.2 手动完成CompletableFuture 2.3 异常完成CompletableFuture 三、异步计算和回调 3.1 异步任务的执行 3.2 处理计算结果 四、组合多个…...

【Linux】初识Linux和Linux环境配置
1.什么是Linux操作系统 说到电脑系统 我想有大多数人会脱口而出:windows、mac 是的,这也是如今市场上主流的两种操作系统。 但是对于IT相关的人士来说,还有一种系统也是必须有姓名 那就是Linux Linux,Linux Is Not UniX 的…...
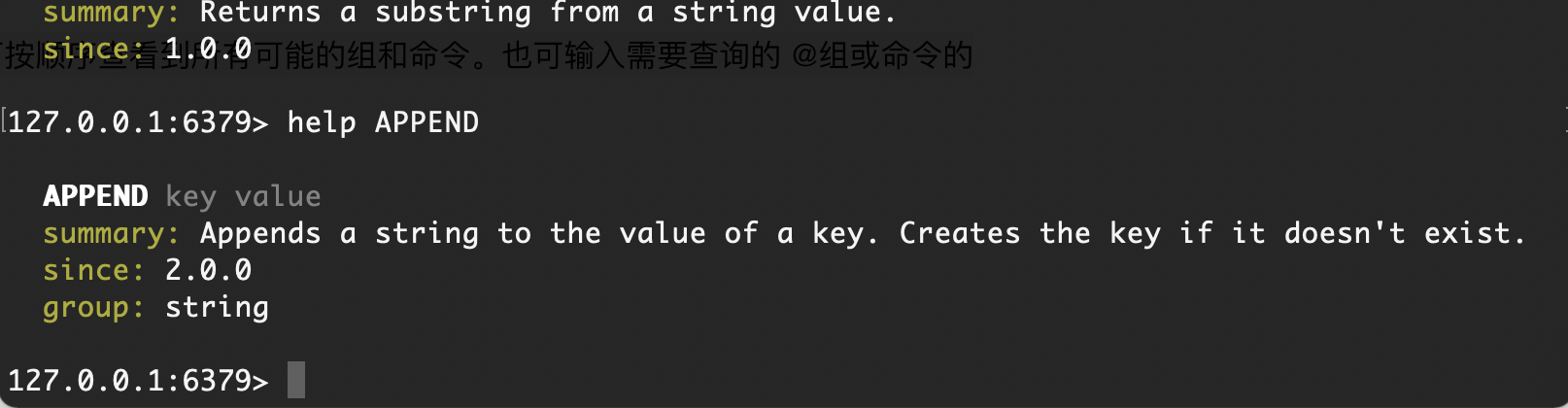
redis-cli help使用
1. redis-cli命令使用—先连接上服务器 连接到 Redis 服务器: 使用 redis-cli 命令即可连接到本地运行的 Redis 服务器,默认连接到本地的 6379 端口。 redis-cli如果 Redis 服务器不在本地或者端口不同,可以使用 -h 和 -p 参数指定主机和端…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...