【九十七】【算法分析与设计】图论,迷宫,1207. 大臣的旅费,走出迷宫,石油采集,after与迷宫,逃离迷宫,3205. 最优配餐,路径之谜
1207. 大臣的旅费 - AcWing题库
很久以前,TT 王国空前繁荣。
为了更好地管理国家,王国修建了大量的快速路,用于连接首都和王国内的各大城市。
为节省经费,TT 国的大臣们经过思考,制定了一套优秀的修建方案,使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。
同时,如果不重复经过大城市,从首都到达每个大城市的方案都是唯一的。
JJ 是 TT 国重要大臣,他巡查于各大城市之间,体察民情。
所以,从一个城市马不停蹄地到另一个城市成了 JJ 最常做的事情。
他有一个钱袋,用于存放往来城市间的路费。
聪明的 JJ 发现,如果不在某个城市停下来修整,在连续行进过程中,他所花的路费与他已走过的距离有关。
具体来说,一段连续的旅途里,第 11 千米的花费为 1111,第 22 千米的花费为 1212,第 33 千米的花费为 1313,…,第 xx 千米的花费为 x+10x+10。
也就是说,如果一段旅途的总长度为 11 千米,则刚好需要花费 1111,如果一段旅途的总长度为 22 千米,则第 11 千米花费 1111,第 22 千米花费 1212,一共需要花费 11+12=2311+12=23。
JJ 大臣想知道:他从某一个城市出发,中间不休息,到达另一个城市,所有可能花费的路费中最多是多少呢?
输入格式
输入的第一行包含一个整数 nn,表示包括首都在内的 TT 王国的城市数。
城市从 11 开始依次编号,11 号城市为首都。
接下来 n−1n−1 行,描述 TT 国的高速路(TT 国的高速路一定是 n−1n−1 条)。
每行三个整数 Pi,Qi,DiPi,Qi,Di,表示城市 PiPi 和城市 QiQi 之间有一条双向高速路,长度为 DiDi 千米。
输出格式
输出一个整数,表示大臣 JJ 最多花费的路费是多少。
数据范围
1≤n≤1051≤n≤105,
1≤Pi,Qi≤n1≤Pi,Qi≤n,
1≤Di≤10001≤Di≤1000
输入样例:
5 1 2 2 1 3 1 2 4 5 2 5 4
输出样例:
135
1.
树的直径,树中两点之间的距离的最大值是多少?求这个值的做法是,先随便找一个点,然后找到距离该点最远距离的点A,再找到距离A点最远距离的点B,AB两点的距离就是最大直径.
2.
用dfs可以找到A点最远点B和对应的距离.
dfs遍历每一个点,对于每一个点都具有一个信息,距离A点的距离是多少,作为节点信息.
3.
用邻接表存储图的信息.
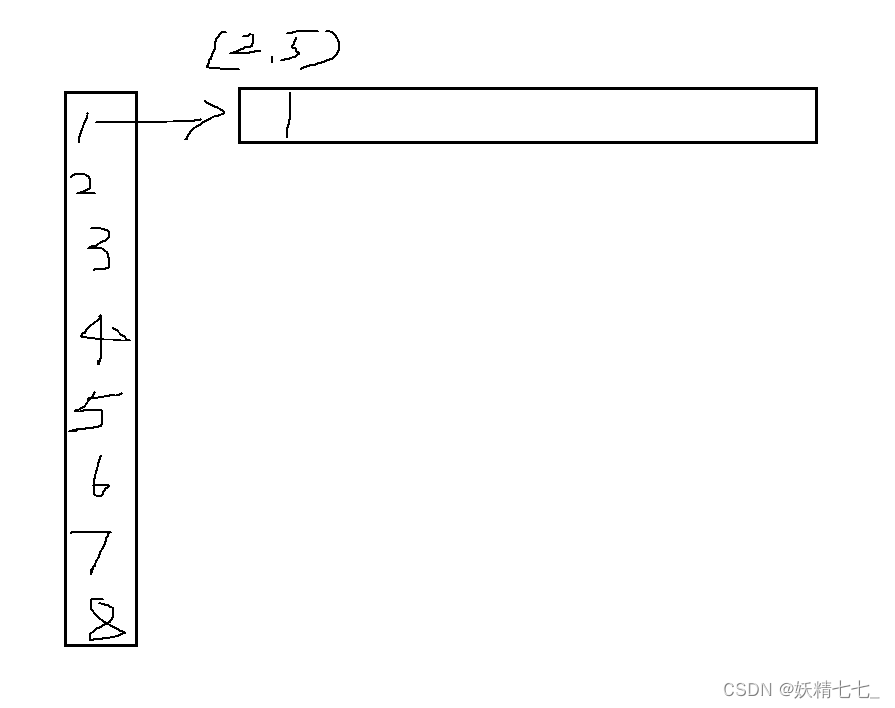
用一个vector<vector<p>> g;类型表示邻接表,外层vector下标表示每一个点,每一个点对应的vector存储pair<int,int>类型,表示从下标点可以走到的点和距离.
#include<bits/stdc++.h>
using namespace std;
#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义换行符using p=pair<int,int>; // 定义 pair<int, int> 类型的别名为 pint n; // 城市数量
vector<vector<p>> g; // 邻接表表示的图int ret; // 存储最长路径长度
int lastpos; // 存储最长路径的终点
vector<bool>visited; // 访问标记数组// 深度优先搜索函数
void dfs(int i,int path){if(path>ret)lastpos=i; // 如果当前路径长度大于已知最长路径,更新终点位置ret=max(ret,path); // 更新最长路径长度visited[i]=true; // 标记当前节点已访问for(auto&x:g[i]){ // 遍历当前节点的邻接节点if(!(visited[x.first]))dfs(x.first,path+x.second); // 如果邻接节点未访问,继续递归搜索}visited[i]=false; // 回溯,标记当前节点未访问
}// 初始化函数
void init(){ret=0,lastpos=0; // 初始化最长路径长度和终点位置visited.assign(n+1,false); // 初始化访问标记数组}// 求解函数
void solve(){dfs(1,0); // 从节点 1 开始第一次深度优先搜索dfs(lastpos,0); // 从第一次搜索到的终点开始第二次深度优先搜索cout << (ret * ret + 21 * ret) / 2; // 输出结果,计算最大花费
}// 主函数
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); // 加速输入输出cin>>n; // 输入城市数量g.assign(n+1,vector<p>()); // 初始化邻接表for(int i=1;i<=n-1;i++){int start,end,length;cin>>start>>end>>length; // 输入每条边的信息g[start].push_back({end,length}); // 添加边到邻接表g[end].push_back({start,length}); // 添加边到邻接表(双向)}init(); // 调用初始化函数solve(); // 调用求解函数
}
走出迷宫
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网
题目描述
小明现在在玩一个游戏,游戏来到了教学关卡,迷宫是一个N*M的矩阵。
小明的起点在地图中用“S”来表示,终点用“E”来表示,障碍物用“#”来表示,空地用“.”来表示。
障碍物不能通过。小明如果现在在点(x,y)处,那么下一步只能走到相邻的四个格子中的某一个:(x+1,y),(x-1,y),(x,y+1),(x,y-1);
小明想要知道,现在他能否从起点走到终点。
输入描述:
本题包含多组数据。
每组数据先输入两个数字N,M
接下来N行,每行M个字符,表示地图的状态。
数据范围:
2<=N,M<=500
保证有一个起点S,同时保证有一个终点E.
输出描述:
每组数据输出一行,如果小明能够从起点走到终点,那么输出Yes,否则输出No
示例1
输入
复制3 3 S.. ..E ... 3 3 S## ### ##E
3 3
S..
..E
...
3 3
S##
##E
输出
复制Yes No
Yes
No
1.
迷宫从某一个点出发,寻找是否存在一条路径到达另一个指定点,只需要用dfs遍历所有的可以走的位置即可.
用一个visited存储可以走的路径和不可以走的路径,走过的路径是不可以走的位置.
2.
找某点到另一个点是否有路径,不需要回溯操作,回溯操作有点时候会导致时间复杂度变大.
这道题回溯会导致时间超时.
#include<bits/stdc++.h>
using namespace std;
#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义换行符using p = pair<int, int>; // 定义 pair<int, int> 类型的别名为 p
p start, end1; // 定义起点和终点int n, m; // 定义迷宫的行数和列数
vector<vector<char>> g; // 定义迷宫的矩阵vector<p> d = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 定义四个移动方向:右、下、左、上
vector<vector<bool>> visited; // 定义访问标记矩阵// 深度优先搜索函数,判断是否能从起点到达终点
bool dfs(int i, int j) {if (i == end1.first && j == end1.second) { // 如果当前点是终点,返回 truereturn true;}visited[i][j] = true; // 标记当前点已访问for (auto& dd : d) { // 遍历四个方向int x = i + dd.first;int y = j + dd.second;if (x >= 0 && x < n && y >= 0 && y < m && !visited[x][y]) { // 判断新位置是否在边界内且未访问if (dfs(x, y)) return true; // 递归搜索,如果找到路径返回 true}}// visited[i][j] = false; // 不需要回溯return false; // 如果所有方向都无法到达终点,返回 false
}// 初始化函数
void init() {visited.assign(n, vector<bool>(m, false)); // 初始化访问标记矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (g[i][j] == '#') visited[i][j] = true; // 将障碍物标记为已访问}}
}// 求解函数
void solve() {if (dfs(start.first, start.second)) { // 从起点开始深度优先搜索cout << "Yes" << endl; // 如果可以到达终点,输出 "Yes"} else {cout << "No" << endl; // 否则输出 "No"}
}// 主函数
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出while (cin >> n >> m) { // 输入迷宫的行数和列数g.assign(n, vector<char>(m)); // 初始化迷宫矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {cin >> g[i][j]; // 输入迷宫的每个字符if (g[i][j] == 'S') {start = {i, j}; // 找到起点位置}if (g[i][j] == 'E') {end1 = {i, j}; // 找到终点位置}}}init(); // 调用初始化函数solve(); // 调用求解函数}
}
石油采集
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网
题目描述
随着海上运输石油泄漏的问题,一个新的有利可图的行业正在诞生,那就是撇油行业。如今,在墨西哥湾漂浮的大量石油,吸引了许多商人的目光。这些商人们有一种特殊的飞机,可以一瓢略过整个海面20米乘10米这么大的长方形。(上下相邻或者左右相邻的格子,不能斜着来)当然,这要求一瓢撇过去的全部是油,如果一瓢里面有油有水的话,那就毫无意义了,资源完全无法利用。现在,商人想要知道,在这片区域中,他可以最多得到多少瓢油。
地图是一个N×N的网络,每个格子表示10m×10m的正方形区域,每个区域都被标示上了是油还是水
输入描述:
测试输入包含多条测试数据
测试数据的第一行给出了测试数据的数目T(T<75)
每个测试样例都用数字N(N<50)来表示地图区域的大小,接下来N行,每行都有N个字符,其中符号’.’表示海面、符号’#’表示油面。
输出描述:
输出格式如下“Case X: M”(X从1开始),M是商人可以最多得到的油量。
示例1
输入
复制1 6 ...... .##... ...... .#..#. .#..## ......
1
6
......
.##...
......
.#..#.
.#..##
......
输出
复制Case 1: 3
Case 1: 3
1.
找网格中具有多少个1x2的矩形,计算横纵坐标累加值的奇数和偶数的个数,具有的矩形个数是min(odd,even).
odd是奇数,even是偶数.
#include<bits/stdc++.h>
using namespace std;
#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义换行符
using p=pair<int,int>; // 定义 pair<int, int> 类型的别名为 pvector<p>d={{0,1},{1,0},{0,-1},{-1,0}}; // 定义四个移动方向:右、下、左、上int t, n; // 测试数据的数量和地图区域的大小
vector<vector<char>> g; // 定义地图矩阵int ret; // 记录最多可以撇油的数量
int even, odd; // 记录偶数和奇数格子的数量
int count1=1; // 记录测试用例编号// 深度优先搜索函数,用于遍历油区域
void dfs(int i, int j) {if((i+j)&1) odd++; // 如果 (i+j) 是奇数,odd++else even++; // 否则 even++if(g[i][j]=='#') g[i][j]='.'; // 将当前油格子标记为已访问for(auto& dd : d) { // 遍历四个方向int x = i + dd.first;int y = j + dd.second;if(x >= 0 && x < n && y >= 0 && y < n && g[x][y] == '#') { // 判断新位置是否在边界内且是油dfs(x, y); // 递归搜索}}
}// 初始化函数
void init() {ret = 0, even = 0, odd = 0; // 初始化变量
}// 求解函数
void solve() {for(int i = 0; i < n; i++) {for(int j = 0; j < n; j++) {even = 0, odd = 0; // 每次搜索前重置计数器if(g[i][j] == '#') dfs(i, j); // 如果当前格子是油,开始深度优先搜索ret += min(even, odd); // 取偶数和奇数中的最小值累加到结果中}}cout << "Case " << count1++ << ": " << ret << endl; // 输出结果
}// 主函数
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出cin >> t; // 输入测试数据的数量while(t--) { // 处理每组测试数据cin >> n; // 输入地图区域的大小g.assign(n, vector<char>(n)); // 初始化地图矩阵for(int i = 0; i < n; i++) {for(int j = 0; j < n; j++) {cin >> g[i][j]; // 输入地图的每个字符}}init(); // 调用初始化函数solve(); // 调用求解函数}
}
after与迷宫
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网
题目描述
after的算法书的遗落在一个叫做AIJ的迷宫中了,这个迷宫有N*M个房间,迷宫的入口为(1,1),算法书遗落在(r,c)。迷宫中的房间有四种状态:空房间、无法进入的房间、有墨菲斯托存在的房间和有莉莉丝存在的房间。墨菲斯托会否定一切,而莉莉丝会诱惑人做一种叫做YK的活动。after是一个意志薄弱的人,他遇到了墨菲斯托和莉莉丝之后,便会变成眼神空洞的超级YK机器人。after每步可以从他当前的房间走至上下左右四个房间的其中一个房间。after害怕变成超级YK机器人,所以要尽快拿到算法书然后从入口逃离。问after最少需要走多少步才可以在不变成超级YK机器人的情况下从入口出发取回算法书并逃离迷宫?
输入描述:
第一行一个正整数T(T<=10),表示共有T组数据。
对于每组数据,第一行四个正整数N,M,r,c(1<=N,M<=1000;1<=r<=N;1<=c<=M)。
接下来N行,每行M个字符,每个表示房间的状态,“.”表示空房间,“*”表示无法进入的房间,“F”表示有墨菲斯托存在的房间,“M”表示有莉莉丝存在的房间。
数据保证(1,1)为“.”。
输出描述:
对每组数据输出一行,即after最少需要走的步数。若after无法取回算法书,则输出“IMPOSSIBLE”(不带引号)。
示例1
输入
复制1 4 4 4 3 ..** *F.. *.*. *M.F
1
4 4 4 3
..**
*F..
..
*M.F
输出
复制14
14
1.
不能够同时遇到F和M,所以有两种情况,允许遇到F或者允许遇到M.找最短的距离,从出发点前往魔法书的位置然后还需要返回到出发点,距离乘以2即可.
2.
bfs维护存储出发点到所有位置的最短距离.
#include<bits/stdc++.h>
using namespace std;
#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义换行符
using p = pair<int, int>; // 定义 pair<int, int> 类型的别名为 pvector<p> d = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 定义四个移动方向:右、下、左、上int t; // 测试数据的数量
int n, m, r, c; // 地图的行数、列数,以及算法书的位置vector<vector<char>> g; // 定义地图矩阵
vector<vector<int>> dis1; // 定义从起点到各位置的最短距离矩阵(允许遇到 F)
vector<vector<int>> dis2; // 定义从起点到各位置的最短距离矩阵(允许遇到 M)
int ret; // 记录最终结果// 广度优先搜索函数,用于计算最短路径
void bfs(vector<vector<int>>& dis, char ch) {queue<p> q; // 定义队列用于 BFSq.push({0, 0}); // 从起点开始dis[0][0] = 0; // 起点到自己的距离为 0while (!q.empty()) {auto top = q.front(); // 获取队首元素q.pop(); // 弹出队首元素int i = top.first, j = top.second; // 当前坐标if (i == r && j == c) return; // 如果到达目标位置,返回for (auto& dd : d) { // 遍历四个方向int x = i + dd.first;int y = j + dd.second;// 判断新位置是否在边界内,且不是障碍物、指定角色,且未被访问if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] != '*' && g[x][y] != ch && dis[x][y] == LLONG_MAX) {dis[x][y] = dis[i][j] + 1; // 更新新位置的距离q.push({x, y}); // 将新位置加入队列}}}
}// 初始化函数
void init() {ret = 0; // 重置结果dis1.assign(n, vector<int>(m, LLONG_MAX)); // 初始化距离矩阵,设为无穷大dis2.assign(n, vector<int>(m, LLONG_MAX)); // 初始化距离矩阵,设为无穷大
}// 求解函数
void solve() {bfs(dis1, 'F'); // 计算不遇到 F 的最短路径bfs(dis2, 'M'); // 计算不遇到 M 的最短路径ret = min(dis1[r][c], dis2[r][c]); // 取两种情况中的最短距离if (ret != LLONG_MAX)cout << 2 * ret << endl; // 输出最短路径长度的两倍else cout << "IMPOSSIBLE" << endl; // 如果无法到达,输出 "IMPOSSIBLE"
}// 主函数
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出cin >> t; // 输入测试数据的数量while (t--) { // 处理每组测试数据cin >> n >> m >> r >> c; // 输入地图的行数、列数,以及算法书的位置r--, c--; // 将算法书位置调整为从 0 开始的索引g.assign(n, vector<char>(m)); // 初始化地图矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {cin >> g[i][j]; // 输入地图的每个字符}}init(); // 调用初始化函数solve(); // 调用求解函数}
}
逃离迷宫
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网
题目描述
给你一个n*m的图,地图上'.'代表可以走的地方,而'#'代表陷阱不能走,
'P'代表人物位置,'K'代表钥匙,'E'代表出口。人物一个,钥匙有多个,
('K'的数量<=50)),出口一个,每个位置可以向(上,下,左,右)四个
方向走一格,花费一个单位时间,现在你需要花费最少的时间拿到钥匙
然后从迷宫的出口出去(若没有钥匙,则不能进入迷宫出口所在的格子)。
输入描述:
第一行一个整数T(T <= 50),代表数据的组数
接下来一行n,m(n<=500,m<=500),代表地图的行和列
接下来n行,每行一个长度为m的字符串,组成一个图。
输出描述:
如果可以出去,输出所花费的最少时间。
如果不能出去,输出一行"No solution"。
示例1
输入
复制3 5 5 ....P ##..E K#... ##... ..... 5 5 P.... ..... ..E.. ..... ....K 5 5 P#..E .#.#. .#.#. .#.#. ...#K
3
5 5
....P
##..E
K#...
##...
.....
5 5
P....
.....
..E..
.....
....K
5 5
P#..E
.#.#.
.#.#.
.#.#.
...#K
输出
复制No solution 12 No solution
No solution
12
No solution
1.
入口,钥匙点,出口,我们需要从入口到达其中一个钥匙点,然后去出口,求最短的距离.
存储入口到所有位置的最短距离,和出口到所有位置的最短距离,遍历每一个钥匙点,如果距离存在,找最短就可以了.
#include<bits/stdc++.h>
using namespace std;
#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义换行符
using p = pair<int, int>; // 定义 pair<int, int> 类型的别名为 pvector<p> d = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 定义四个移动方向:右、下、左、上int t, n, m; // t 为测试数据的数量,n 为地图的行数,m 为地图的列数
vector<vector<char>> g; // 定义地图矩阵vector<vector<int>> dis1; // 定义从起点到各位置的最短距离矩阵
vector<vector<int>> dis2; // 定义从出口到各位置的最短距离矩阵
p start, end1; // 定义起点和终点
int ret; // 记录最终结果
vector<p> yaoshi; // 定义钥匙的位置列表// 广度优先搜索函数,用于计算最短路径
void bfs(vector<vector<int>>& dis, p point) {dis[point.first][point.second] = 0; // 起点距离为 0queue<p> q; // 定义队列用于 BFSq.push(point); // 将起点加入队列while (!q.empty()) {auto top = q.front(); // 获取队首元素q.pop(); // 弹出队首元素int i = top.first; // 当前坐标int j = top.second; // 当前坐标if (point == start && i == end1.first && j == end1.second) continue; // 如果是起点且到达终点,继续for (auto& dd : d) { // 遍历四个方向int x = i + dd.first; // 新位置的行坐标int y = j + dd.second; // 新位置的列坐标// 判断新位置是否在边界内,且不是陷阱,且未被访问if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] != '#' && dis[x][y] == LLONG_MAX) {q.push({x, y}); // 将新位置加入队列dis[x][y] = dis[i][j] + 1; // 更新新位置的距离}}}
}// 初始化函数
void init() {dis1.assign(n, vector<int>(m, LLONG_MAX)); // 初始化距离矩阵,设为无穷大dis2.assign(n, vector<int>(m, LLONG_MAX)); // 初始化距离矩阵,设为无穷大ret = LLONG_MAX; // 初始化结果为无穷大
}// 求解函数
void solve() {bfs(dis1, start); // 计算从起点到各位置的最短路径bfs(dis2, end1); // 计算从出口到各位置的最短路径for (auto& x : yaoshi) { // 遍历所有钥匙位置int i = x.first; // 钥匙的行坐标int j = x.second; // 钥匙的列坐标// 判断起点到钥匙和出口到钥匙的距离是否存在if (dis1[i][j] != LLONG_MAX && dis2[i][j] != LLONG_MAX) {ret = min(ret, dis1[i][j] + dis2[i][j]); // 更新最短路径}}if (ret != LLONG_MAX) cout << ret << endl; // 输出最短路径else cout << "No solution" << endl; // 如果无法到达,输出 "No solution"
}// 主函数
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出cin >> t; // 输入测试数据的数量while (t--) { cin >> n >> m; // 输入地图的行数和列数g.assign(n, vector<char>(m)); // 初始化地图矩阵yaoshi.clear(); // 清空钥匙列表for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {cin >> g[i][j]; // 输入地图的每个字符if (g[i][j] == 'P') { // 如果是人物位置start.first = i;start.second = j;}if (g[i][j] == 'E') { // 如果是出口位置end1.first = i;end1.second = j;}if (g[i][j] == 'K') { // 如果是钥匙位置yaoshi.push_back({i, j});}}}init(); // 调用初始化函数solve(); // 调用求解函数}return 0;
}
3205. 最优配餐 - AcWing 题库
栋栋最近开了一家餐饮连锁店,提供外卖服务。
随着连锁店越来越多,怎么合理的给客户送餐成为了一个急需解决的问题。
栋栋的连锁店所在的区域可以看成是一个 n×nn×n 的方格图(如下图所示),方格的格点上的位置上可能包含栋栋的分店(绿色标注)或者客户(蓝色标注),有一些格点是不能经过的(红色标注)。
方格图中的线表示可以行走的道路,相邻两个格点的距离为 11。
栋栋要送餐必须走可以行走的道路,而且不能经过红色标注的点。
送餐的主要成本体现在路上所花的时间,每一份餐每走一个单位的距离需要花费 11 块钱。
每个客户的需求都可以由栋栋的任意分店配送,每个分店没有配送总量的限制。
现在你得到了栋栋的客户的需求,请问在最优的送餐方式下,送这些餐需要花费多大的成本。
输入格式
输入的第一行包含四个整数 n,m,k,dn,m,k,d,分别表示方格图的大小、栋栋的分店数量、客户的数量,以及不能经过的点的数量。
接下来 mm 行,每行两个整数 xi,yixi,yi,表示栋栋的一个分店在方格图中的横坐标和纵坐标。
接下来 kk 行,每行三个整数 xi,yi,cixi,yi,ci,分别表示每个客户在方格图中的横坐标、纵坐标和订餐的量。(注意,可能有多个客户在方格图中的同一个位置)
接下来 dd 行,每行两个整数,分别表示每个不能经过的点的横坐标和纵坐标。
输出格式
输出一个整数,表示最优送餐方式下所需要花费的成本。
数据范围
前 30%30% 的评测用例满足:1≤n≤201≤n≤20。
前 60%60% 的评测用例满足:1≤n≤1001≤n≤100。
所有评测用例都满足:1≤n≤1000,1≤m,k,d≤n2,1≤xi,yi≤n1≤n≤1000,1≤m,k,d≤n2,1≤xi,yi≤n。
可能有多个客户在同一个格点上。
每个客户的订餐量不超过 10001000,每个客户所需要的餐都能被送到。
输入样例:
10 2 3 3 1 1 8 8 1 5 1 2 3 3 6 7 2 1 2 2 2 6 8
输出样例:
29
1.
多源最短路径,我们要求客户点距离多个商家位置的最短距离,例如客户点A距离商家B,C最短距离.
将B,C点依次加入到队列中,然后bfs维护数据距离.
2.
用dis存储每一个点到达某一个商家点的最短距离,遍历所有的客户点,距离乘以订单数即可.
#include<bits/stdc++.h>
using namespace std;
#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义换行符
using p = pair<int, int>; // 定义 pair<int, int> 类型的别名为 pvector<p> d1 = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 定义四个移动方向:右、下、左、上int n, m, k, d; // n 为方格图的大小,m 为分店数量,k 为客户数量,d 为不能经过的点的数量
vector<p> fendian; // 定义分店位置列表
struct node { // 定义客户节点结构体int x, y; // 客户的坐标int count; // 客户的订餐量
};
vector<node> kehu; // 定义客户列表
vector<vector<int>> dis; // 定义距离矩阵
int ret; // 记录最终结果// 广度优先搜索函数,用于计算最短路径
void bfs() {queue<p> q; // 定义队列用于 BFSfor (auto& xx : fendian) { // 将所有分店位置加入队列q.push(xx);dis[xx.first][xx.second] = 0; // 分店位置距离自身为 0}while (!q.empty()) {auto top = q.front(); // 获取队首元素q.pop(); // 弹出队首元素int i = top.first; // 当前坐标int j = top.second; // 当前坐标for (auto& dd : d1) { // 遍历四个方向int x = i + dd.first; // 新位置的行坐标int y = j + dd.second; // 新位置的列坐标// 判断新位置是否在边界内,且未被访问if (x >= 0 && x < n && y >= 0 && y < n && dis[x][y] == -1) {q.push({x, y}); // 将新位置加入队列dis[x][y] = dis[i][j] + 1; // 更新新位置的距离}}}
}// 求解函数
void solve() {bfs(); // 调用 BFS 函数计算最短路径for (auto& xx : kehu) { // 遍历所有客户ret += dis[xx.x][xx.y] * xx.count; // 计算每个客户的配送成本并累加}cout << ret << endl; // 输出最终结果
}// 主函数
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出cin >> n >> m >> k >> d; // 输入方格图的大小、分店数量、客户数量以及不能经过的点的数量fendian.assign(m, p()); // 初始化分店列表kehu.assign(k, node()); // 初始化客户列表dis.assign(n, vector<int>(n, -1)); // 初始化距离矩阵,设为 -1for (int i = 0; i < m; i++) {cin >> fendian[i].first >> fendian[i].second; // 输入每个分店的位置fendian[i].first--; // 将坐标转换为从 0 开始fendian[i].second--;}for (int i = 0; i < k; i++) {cin >> kehu[i].x >> kehu[i].y >> kehu[i].count; // 输入每个客户的位置及订餐量kehu[i].x--; // 将坐标转换为从 0 开始kehu[i].y--;}for (int i = 0; i < d; i++) {int x, y;cin >> x >> y; // 输入每个不能经过的点的位置x--, y--; // 将坐标转换为从 0 开始dis[x][y] = LLONG_MAX; // 将不能经过的点标记为无穷大}solve(); // 调用求解函数return 0;
}
路径之谜
题目描述
小明冒充X星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是nxn个方格。如下图所示
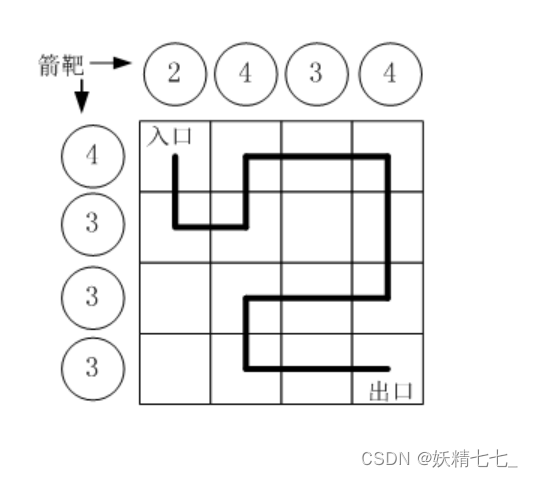
按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃,每走到一个新方格,就要向正北方和正西方各射一箭。(城堡
的西墙和北墙内各有12个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时
是可以的,比如上图中的例子。
本题的要求就是已知简靶数字,求骑士的行走路径(测试数据保证路径唯一
输入描述
第一行一个整数N(0<N<20),表示地面有NXN个方格。
第二行N个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行N个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出描述
输出一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号号:0,1,2,3-
比如,上图中的方块编号为:
0123
4567
891011
12131415
输入输出样例
示例
输入
4333
输出
045123711109131415
运行限制
最大运行时间:5s
最大运行内存:256M
1.
网格(i,j)坐标转化为数字的公式是i*col+j.
dfs遍历网格每一个点,到达每一个点的时候维护节点的信息.
节点信息,是所走路径导致的靶子上箭的数量.
2.
剪枝操作,当维护当前节点箭数量之后,当前箭数量大于对应目标箭数量,此时不需要再继续了,因为箭的数量只能增加不能减少.
如果到达了终点,箭数量有一个不对,就返回.
3.
goto flag1;
flag1:
组合起来可以传送操作.
#include<bits/stdc++.h>
using namespace std;
#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义换行符
using p = pair<int, int>; // 定义 pair<int, int> 类型的别名为 pvector<p> d = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 定义四个移动方向:右、下、左、上int n; // 定义地面的大小 n*n
vector<int> aim1; // 北边的箭靶上的数字
vector<int> aim2; // 西边的箭靶上的数字vector<int> nowaim1; // 当前北边的箭数量
vector<int> nowaim2; // 当前西边的箭数量
vector<int> path; // 记录骑士的路径
vector<vector<bool>> visited; // 记录每个方格是否被访问// 深度优先搜索函数,判断是否可以通过当前路径到达终点
bool dfs(int i, int j) {visited[i][j] = true; // 标记当前方格已访问nowaim1[j]++; // 当前列的箭数量加一nowaim2[i]++; // 当前行的箭数量加一path.push_back(i * n + j); // 将当前方格编号加入路径// 剪枝:如果当前箭数量超过目标箭数量,回溯if (nowaim1[j] > aim1[j] || nowaim2[i] > aim2[i]) goto flag1;// 如果到达终点,检查所有箭数量是否符合目标if (i == n - 1 && j == n - 1) {for (int k = 0; k < n; k++) {if (nowaim1[k] != aim1[k] || nowaim2[k] != aim2[k]) goto flag1;}return true; // 路径符合要求,返回 true}// 继续搜索四个方向for (auto& xx : d) {int x = i + xx.first;int y = j + xx.second;if (x >= 0 && x < n && y >= 0 && y < n && !visited[x][y]) {if (dfs(x, y)) return true; // 如果找到路径,返回 true}}// 回溯操作flag1:nowaim1[j]--;nowaim2[i]--;visited[i][j] = false;path.pop_back();return false; // 返回 false,表示当前路径不符合要求
}// 求解函数
void solve() {dfs(0, 0); // 从起点开始深度优先搜索for (auto& x : path) {cout << x << " "; // 输出路径}cout << endl;
}// 主函数
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出cin >> n; // 输入地面的大小aim1.assign(n, 0); // 初始化北边的箭靶数字aim2.assign(n, 0); // 初始化西边的箭靶数字nowaim1.assign(n, 0); // 初始化当前北边的箭数量nowaim2.assign(n, 0); // 初始化当前西边的箭数量visited.assign(n, vector<bool>(n, false)); // 初始化访问矩阵for (int i = 0; i < n; i++) cin >> aim1[i]; // 输入北边的箭靶数字for (int i = 0; i < n; i++) cin >> aim2[i]; // 输入西边的箭靶数字solve(); // 调用求解函数
}
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【九十七】【算法分析与设计】图论,迷宫,1207. 大臣的旅费,走出迷宫,石油采集,after与迷宫,逃离迷宫,3205. 最优配餐,路径之谜
1207. 大臣的旅费 - AcWing题库 很久以前,TT 王国空前繁荣。 为了更好地管理国家,王国修建了大量的快速路,用于连接首都和王国内的各大城市。 为节省经费,TT 国的大臣们经过思考,制定了一套优秀的修建方案,…...

【Tools】SpringBoot工程中,对于时间属性从后端返回到前端的格式问题
Catalog 时间属性格式问题一、需求二、怎么使用 时间属性格式问题 一、需求 对于表中时间字段,后端创建对应的实体类的时间属性需要设定格式(默认的格式不方便阅读),再返回给前端。 二、怎么使用 导入jackson相关的坐标&#x…...

算法训练营day35
题目1:122. 买卖股票的最佳时机 II - 力扣(LeetCode) 贪心算法思路很简单,就是把每一天的利润都算出来,然后把整的加起来就是结果 class Solution { public:int maxProfit(vector<int>& prices) {int resu…...
代码随想录-Day23
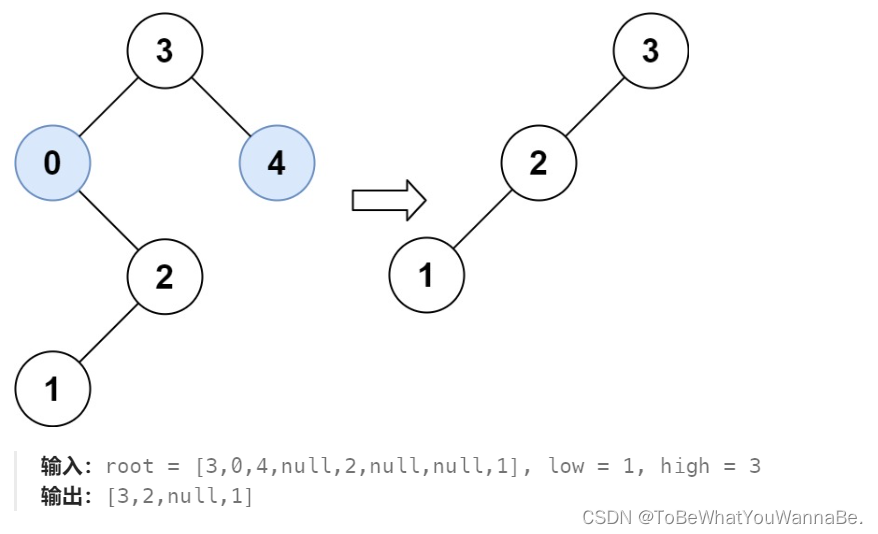
669. 修剪二叉搜索树 方法一:递归 class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if (root null) {return null;}if (root.val < low) {return trimBST(root.right, low, high);} else if (root.val > high) {return trimBS…...
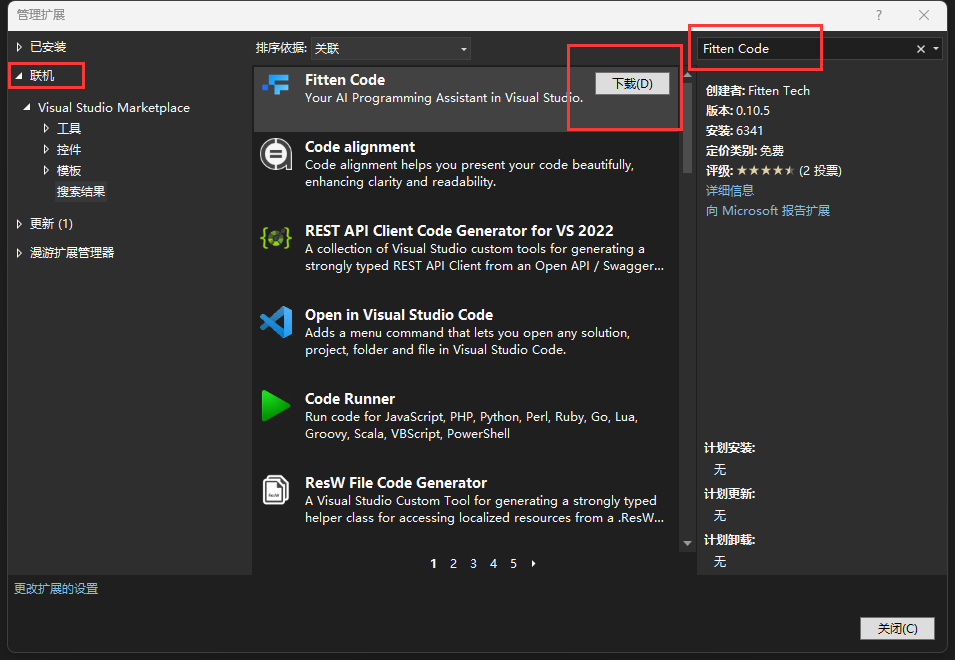
基于Visual Studio版本的AI编程助手
Visual Studio 是一个出色的 IDE,可用于构建适用于 Windows、Mac、Linux、iOS 和 Android 的丰富、精美的跨平台应用程序。 使用一系列技术(例如 WinForms、WPF、WinUI、MAUI 或 Xamarin)构建丰富。 1、安装 点击上方工具栏拓展选项,选择管理拓展选项 接着在联机页面中搜索&q…...
04-Vue:ref获取页面节点--很简单
目录 前言在Vue中,通过 ref 属性获取DOM元素使用 ref 属性获取整个子组件(父组件调用子组件的方法) 前言 我们接着上一篇文章 03-02-Vue组件之间的传值 来讲。 下一篇文章 05-Vue路由 在Vue中,通过 ref 属性获取DOM元素 我们当然…...

CBK-D2-安全与架构工程.md
CBK-D2-安全与架构工程 密码学和对称密钥算法 密码通信的基础知识 明文P-plaintext、加密encrypt、密文C-ciphertext、解密decrypt、密钥Key 多数情况下,密钥无非是一个极大的二进制数 每一种算法都有一个特定密钥控制key space,是一个特定的数值范围 密钥空间由位大小b…...

Windows驱动开发系列文章一
文章目录 环境搭建如何调试实时调试非实时调试 环境搭建 基本上按照官方网站安装 VisualStudio/SDK/WDK 这些软件就可以了 详情请参考这个安装链接 如何调试 Windows 调试分为两种:一种是实时调试,一种是非实时调试 实时调试 这个就需要用到Microso…...

java项目之人事系统源码(springboot+vue+mysql)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的人事系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 项目简介: 基于vue的人事系统的主要使用者…...

I/O '24|学习资源焕新,技术灵感升级
2024 年 5 月 15 日凌晨举行的 Google I/O 大会为各地的开发者们带来了新的灵感。面对技术革新,相信各位开发者们都迫不及待想要自己上手试一试。 别急,Google 谷歌今年为中国的开发者们准备了一份特别的学习资源,让开发者们自由探索新知。 G…...
前端应用开发实验:表单控件绑定
目录 实验目的相关知识点实验内容代码实现效果 实验目的 (1)熟练掌握应用v-model指令实现双向数据绑定的方法,学会使用 v-model指令绑定文本框、复选框、单选按钮、下拉菜单; (2)学会值绑定(将…...
[双指针] --- 快乐数 盛最多水的容器
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏: 算法Journey 本篇博客我们分享一下双指针算法中的快慢指针以及对撞双指针,下面我们开始今天的学习吧~ 🏠 快乐数 📒 题…...
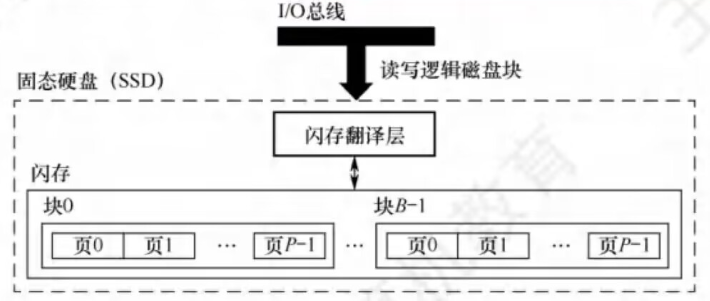
操作系统 - 输入/输出(I/O)管理
输入/输出(I/O)管理 考纲内容 I/O管理基础 设备:设备的基本概念,设备的分类,I/O接口 I/O控制方式:轮询方式,中断方式,DMA方式 I/O软件层次结构:中断处理程序,驱动程序,…...
| 二叉树 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树)
代码随想录算法训练营第22天(py)| 二叉树 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
669. 修剪二叉搜索树 力扣链接 给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>L) 思路 如果当前节点元素小于low,递归右子树,返回符合条件的头节点 如果当前节点元…...

使用C语言实现学生信息管理系统
前言 在我们实现学生信息管理系统的过程中,我们几乎会使用到C语言最常用最重要的知识,对于刚学习完C语言的同学来说是一次很好的巩固机会,其中还牵扯到数据结果中链表的插入和删除内容。 实现学生信息管理系统 文件的创建与使用 对于要实现…...

上下文视觉提示实现zero-shot分割检测及多visual-prompt改造
文章目录 一、Closed-Set VS Open-set二、DINOv2.1 论文和代码2.2 内容2.3 安装部署2.4 使用效果 三、多visual prompt 改造3.1 获取示例图mask3.2 修改函数参数3.3 推理代码3.4 效果的提升! 四、总结 本文主要介绍visual prompt模型DINOv,该模型可输入八…...

WebGL学习(一)渲染关系
学习webgl 开发理解渲染关系是必须的,也非常重要,很多人忽视了这个过程。 我这里先简单写一下,后面尽量用通俗易懂的方式,举例讲解。 WebGL,全称Web Graphics Library,是一种在网页上渲染3D图形的技术。它…...

人生建议:向猫学习
心安理得地被爱 猫从不担心自己不配得到爱,也正是这幅理所应当、宠辱不惊的样子,让人欲罢不能。或许 当你相信自己值得世界上最好的爱时,你就会拥有。 多晒太阳多睡觉 猫喜欢睡觉,尤其喜欢躺阳光好的地方。阳光和睡眠,…...

软件架构设计属性之三:结构性属性浅析
文章目录 引言一、结构性属性的定义二、结构性属性的关键要素1. 组件化2. 模块化3. 层次化4. 接口定义5. 数据流6. 依赖管理 三、结构性属性的设计原则1. 高内聚低耦合2. 松耦合3. 清晰的接口4. 可维护性5. 可扩展性 四、结构性属性的实现策略1. 组件划分2. 模块化设计3. 接口设…...
JAVA:多线程常见的面试题和答案
请关注微信公众号:拾荒的小海螺 博客地址:http://lsk-ww.cn/ 1、并发编程三要素? 原 子 性 原子性指的是一个或者多个操作,要么全部执行并且在执行的过程中不被其他操作打断,要么就全部都不执行。可 见 性 可见性指多…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

