【AI算法岗面试八股面经【超全整理】——概率论】
AI算法岗面试八股面经【超全整理】
- 概率论
- 信息论
- 机器学习
- CV
- NLP
目录
- 1、古典概型、几何概型
- 2、条件概率、全概率公式、贝叶斯公式
- 3、先验概率、后验概率
- 4、离散型随机变量的常见分布
- 5、连续型随机变量的常见分别
- 6、数学期望、方差
- 7、协方差、相关系数
- 8、独立、互斥、不相关
- 9.大数定理
- 10、中心极限定理
- 11、最大似然估计(极大似然估计)
1、古典概型、几何概型
古典概型:(有限等可能)
- 样本空间的数量是有限的
- 每个样本点的发生是等可能性的
几何概型:(无限等可能)
- 样本空间的样本点有无限个
- 每个样本点发生的可能性是均等的
2、条件概率、全概率公式、贝叶斯公式
条件概率
设A、B是两个时间,且 P ( A ) > 1 P(A)>1 P(A)>1代表关节位置,则称 P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)为事件A发生条件下B的条件概率。
- P ( A ) > 0 P(A)>0 P(A)>0时, P ( A B ) = P ( A ) P ( B ∣ A ) P(AB)=P(A)P(B|A) P(AB)=P(A)P(B∣A)
- P ( B ) > 0 P(B)>0 P(B)>0时, P ( A B ) = P ( B ) P ( A ∣ B ) P(AB)=P(B)P(A|B) P(AB)=P(B)P(A∣B)
全概率公式
若事件 A 1 , A 2 , A 3 , ⋯ , A n A_1,A_2, A_3,\cdots,A_n A1,A2,A3,⋯,An满足以下条件:
- ∀ i ≠ j , A i A j = ∅ \forall{i\not=j},A_iAj=\emptyset ∀i=j,AiAj=∅
- A 1 ⋃ A 2 ⋃ A 3 ⋃ ⋯ ⋃ A n = Ω A_1\bigcup A_2\bigcup A_3\bigcup\cdots\bigcup A_n=\Omega A1⋃A2⋃A3⋃⋯⋃An=Ω
则称 A 1 , A 2 , A 3 , ⋯ , A n A_1,A_2, A_3,\cdots,A_n A1,A2,A3,⋯,An为完备事件组
全概率公式为:
P ( B ) = ∑ i = 1 n P ( A i ) P ( B ∣ A i ) \begin{aligned} P(B)=\sum_{i=1}^{n}P(A_i)P(B|A_i) \\ \end{aligned} P(B)=i=1∑nP(Ai)P(B∣Ai)
贝叶斯公式
已知结果找原因,发生了结果B, A k A_k Ak被视作导致B发生的原因
设 A 1 , A 2 , A 3 , ⋯ , A n A_1,A_2, A_3,\cdots,A_n A1,A2,A3,⋯,An为完备事件组,且 P ( A i ) > 0 ( i = 1 , 2 , ⋯ , n ) P(A_i)>0(i=1,2,\cdots,n) P(Ai)>0(i=1,2,⋯,n),B为任意事件, P ( B ) > 0 P(B)>0 P(B)>0,则
P ( A k ∣ B ) = P ( A k ) P ( B ∣ A k ) P ( B ) = P ( A k ) P ( B ∣ A k ) ∑ i = 1 n P ( A i ) P ( B ∣ A i ) \begin{aligned} P(A_k|B)=\frac{P(A_k)P(B|A_k)}{P(B)}= \frac{P(A_k)P(B|A_k)}{\sum_{i=1}^{n}P(A_i)P(B|A_i)}\\ \end{aligned} P(Ak∣B)=P(B)P(Ak)P(B∣Ak)=∑i=1nP(Ai)P(B∣Ai)P(Ak)P(B∣Ak)
通常把 P ( A 1 ) , P ( A 2 ) , … , P ( A n ) P(A_1),P(A_2),\dots,P(A_n) P(A1),P(A2),…,P(An)叫做先验概率,就是在做试验前的概率,而把 P ( A k ∣ B ) ( k = 1 , 2 , … , n ) P(A_k|B)(k=1,2,\dots, n) P(Ak∣B)(k=1,2,…,n)
叫做后验概率。
3、先验概率、后验概率
先验概率
- 由原因推结果
- 事情未发生,只根据以往数据统计,分析事情发生的可能性,即先验概率。
- 先验概率是指根据以往经验和分析得到的概率,如全概率公司,它往往作为“由因求果”问题中的“因”出现。
后验概率
- 由结果推原因
- 事情已发生,已有结果,求引起这件事情发生的因素的可能性,“由果求因”,即后验概率。
- 后验概率是指一句得到的结果信息所计算出的最有可能是哪种事件发生,如贝叶斯公式,是“由因求果”中的因。
全概率公式、贝叶斯公式与先验、后验概率的关系?
- 全概率公式,总结几种因素,事件发生的概率的并集,由因求果
- 贝叶斯公式,事情已经发生,计算引起结果的各因素的概率,由因求果,同后验概率
- 全概率是用原因推结果,贝叶斯是用结果推原因
- 后验概率的计算,是一先验概率为前提条件的,如果只知道事情结果,而不知道先验概率(没有以往数据统计),是无法计算后验概率的。后验概率需要应用到贝叶斯公式。
4、离散型随机变量的常见分布
0-1分布(伯努利分布)
- 随机变量只取0或1两种值(概率分布是p和1-p)
- 随机试验只做一次
X ∼ B ( 1 , p ) \begin{aligned} X\sim B(1,p)\\ \end{aligned} X∼B(1,p)
二项分布(伯努利概型)
- 设试验E只有两种可能结果: A A A及 A ‾ \overline{A} A,则称E为伯努利试验
- 将E独立重复地进行n次,则称这一连串独立的重复试验为n重伯努利分布
随机变量依然也是两种0或1(概率分布是p和1-p),但是此时随机试验做了n次,其中事件X发生了k次
X ∼ B ( n , p ) \begin{aligned} X\sim B(n,p)\\ \end{aligned} X∼B(n,p)
设 P ( A = k ) P(A=k) P(A=k)表示在n次试验里面,事件A发生了k次的概率:
P ( A = k ) = C n k p k ( 1 − p ) n − k \begin{aligned} P(A=k)=C_n^kp^k{(1-p)}^{n-k}\\ \end{aligned} P(A=k)=Cnkpk(1−p)n−k
泊松分布
X ∼ P ( λ ) \begin{aligned} X\sim P(\lambda)\\ \end{aligned} X∼P(λ)
P ( A = k ) = λ k k ! e − λ \begin{aligned} P(A=k)=\frac{\lambda^k }{k!}e^{-\lambda}\\ \end{aligned} P(A=k)=k!λke−λ
几何分布
X ∼ G ( p ) \begin{aligned} X\sim G(p)\\ \end{aligned} X∼G(p)
在伯努利试验中,记每次试验中事件A发生的概率为0,试验进行到时间A出现为止,此时所进行的试验次数为X,其分布律为
P ( A = k ) = ( 1 − p ) k − 1 p ( k = 0 , 1 , 2 , … ) \begin{aligned} P(A=k)={(1-p)}^{k-1}p ~~~~~~ (k=0,1,2,\dots )\\ \end{aligned} P(A=k)=(1−p)k−1p (k=0,1,2,…)
5、连续型随机变量的常见分别
均匀分布
X ∼ U ( a , b ) \begin{aligned} X\sim U(a,b)\\ \end{aligned} X∼U(a,b)
f ( n ) = { 1 b − a , a < x < b 0 other \begin{aligned} f(n)= \begin{cases} \frac{1}{b-a}, & \text {$a<x<b$} \\ 0 & \text{other} \end{cases}\\ \end{aligned} f(n)={b−a1,0a<x<bother
指数分布
X ∼ E ( λ ) \begin{aligned} X\sim E(\lambda)\\ \end{aligned} X∼E(λ)
f ( n ) = { λ e − λ x , x > 0 0 other \begin{aligned} f(n)= \begin{cases}\lambda e^{-\lambda x}, & \text {$x>0$} \\ 0 & \text{other} \end{cases}\\ \end{aligned} f(n)={λe−λx,0x>0other
正态分布/高斯分布
X ∼ N ( μ , σ 2 ) \begin{aligned} X\sim N(\mu, \sigma ^2)\\ \end{aligned} X∼N(μ,σ2)
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 \begin{aligned} f(x)=\frac{1 }{\sqrt{2\pi}\sigma}e^{-\frac{{(x-\mu)^2} }{2\sigma^2}}\\ \end{aligned} f(x)=2πσ1e−2σ2(x−μ)2
特别地,当 μ = 0 , σ = 1 \mu=0,\sigma=1 μ=0,σ=1时为标准正态分布, X ∼ N ( 0 , 1 ) X\sim N(0, 1) X∼N(0,1)
6、数学期望、方差
数学期望
数学期望(或均值、简称期望)是试验中每次可能结果的概率乘以其结果的总和。
方差
方差是衡量源数据与期望值相差的度量值。(平方的期望-期望的平方)
D ( X ) = E ( ( X − E ( X ) ) 2 ) = E ( X 2 ) − E 2 ( X ) D(X)=E({(X-E(X))}^2)=E(X^2)-E^2(X) D(X)=E((X−E(X))2)=E(X2)−E2(X)
7、协方差、相关系数
协方差
期望值分别为 E ( X ) E(X) E(X)与 E ( Y ) E(Y) E(Y)的两个实随机变量X与Y之间的协方差 C o v ( A , Y ) Cov(A,Y) Cov(A,Y)定义为:
C o v ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] = E [ X Y ] − 2 E [ Y ] E [ X ] + E [ X ] E [ Y ] = E [ X Y ] − E [ X ] E [ Y ] Cov(X,Y)=E[(X-E[X])(Y-E[Y])]\\=E[XY]-2E[Y]E[X]+E[X]E[Y]\\=E[XY]-E[X]E[Y] Cov(X,Y)=E[(X−E[X])(Y−E[Y])]=E[XY]−2E[Y]E[X]+E[X]E[Y]=E[XY]−E[X]E[Y]
即X,Y的协方差等于每一个X减去X的平均值乘上每一个Y减去Y的平均值的乘积的和的平均值。
相关系数
(皮尔逊相关系数)
p x y = C o v ( X , Y D ( X ) D ( Y ) p_{xy}=\frac{Cov(X,Y}{\sqrt{D(X)}\sqrt{D(Y)}} pxy=D(X)D(Y)Cov(X,Y
即,用X,Y的协方差除以X的标准差和Y的标准差
8、独立、互斥、不相关
独立
事件A与事件B独立的定义是:
P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
互斥
事件A与事件B互斥的定义是:
集合A与集合B没有相同的样本点,即 A ⋂ B = ∅ A\bigcap B =\empty A⋂B=∅
不相关
事件A与事件B不相关的定义是:
C o v ( A , B ) = E [ A B ] − E [ A ] E [ B ] = 0 Cov(A,B)=E[AB]-E[A]E[B]=0 Cov(A,B)=E[AB]−E[A]E[B]=0
- 如果事件A和事件B发生的概率都不为0,那么独立和互斥有这样一层关系:互斥不独立,独立不互斥
- 在数学期望存在的情况下:独立必不相关,不相关未必独立
9.大数定理
通俗一点来讲,就是样本数量很大的时候,样本均值和数学期望充分接近,也就是说当我们大量重复某一相同的实验的时候,其最后的实验结果可能会稳定在某一数值附近。
如果有一个随机变量X,不断地观察并且采样这个随机变量,得到了n个采样值, X 1 , X 2 , … , X n X_1,X_2,\dots,X_n X1,X2,…,Xn,然后求得这n个采样值的平均值 X ‾ n \overline{X}_n Xn,当n趋于正无穷的时候,这个平均值就收敛于这个随机变量X的期望。
lim n → + ∞ 1 n ∑ i = 1 n x i = μ \lim_{n \to +\infty} \frac{1}{n}\sum_{i=1}^{n}x_i=\mu n→+∞limn1i=1∑nxi=μ
10、中心极限定理
设随机变量 X 1 , X 2 , … , X n X_1,X_2,\dots,X_n X1,X2,…,Xn相互独立,服从同一分布,且具有数学期望和方差: E ( X k ) = μ E(X_k)=\mu E(Xk)=μ, D ( X k ) = θ 2 ( k = 0 , 1 , 2 , … ) D(X_k)=\theta^2(k=0,1,2,\dots) D(Xk)=θ2(k=0,1,2,…),则随机变量之和 ∑ k = 1 n X k \sum_{k=1}^{n}X_k ∑k=1nXk的标准化变量:
Y n = ∑ k = 1 n X k − E ( ∑ k = 1 n X k ) D ( ∑ k = 1 n X k ) = ∑ k = 1 n X k − n μ n θ Y_n=\frac{\sum_{k=1}^{n}X_k-E(\sum_{k=1}^{n}X_k)}{\sqrt{D(\sum_{k=1}^{n}X_k)}}=\frac{\sum_{k=1}^{n}X_k-n\mu}{\sqrt{n}\theta} Yn=D(∑k=1nXk)∑k=1nXk−E(∑k=1nXk)=nθ∑k=1nXk−nμ
对于均值为 μ \mu μ,方差为 θ 2 \theta^2 θ2的独立同分布的随机变量 X 1 , X 2 , … , X n X_1,X_2,\dots,X_n X1,X2,…,Xn之和 ∑ k = 1 n X k \sum_{k=1}^{n}X_k ∑k=1nXk,当n足够大时,有:
1 n ∑ k = 1 n X k − μ θ n ∼ N ( 0 , 1 ) \frac{\frac{1}{n}{\sum_{k=1}^{n}X_k}-\mu}{\frac{\theta}{\sqrt{n}}}\sim N(0,1) nθn1∑k=1nXk−μ∼N(0,1)
N个独立同分布的随机变量,当N充分大时,其均值服从正态分布。
大数定律和中心极限定理的区别
- 大数定理更关注的是样本均值,后者关注的是样本均值的分布。
- 比如掷骰子,假设一轮掷骰子n次,重复了m轮,当n足够大时,大数定理指出这n次的均值等于随机变量的数学期望,而中心极限定理指出这m轮的均值分布符合数学期望的正态分布。
11、最大似然估计(极大似然估计)
一个简单的 n 重伯努利模型(二项分布):事件 A 发生的概率为 p,不发生的概率为 1-p,独立验概 n 次,事件 A 发生 k 次的概率为:
P ( A = k ) = C n k p k ( 1 − p ) n − k P(A=k)=C_n^kp^k{(1-p)}^{n-k} P(A=k)=Cnkpk(1−p)n−k
这是一个概率模型,即已知概率p,求另一些概率,即由因求果
而一个数理统计模型是由果溯因,即求解一下问题,p是多大时,事件A发生k次的概率最大,实际上就是一个求参数问题。
- 概率质量函数(Probability Mass Function,PMF)是离散型随机变量在个特定取值上的概率
- 概率密度函数(Probability Density Function,PDF)是统计学中常用的参数估计方法
最大似然估计(Maximum Likelihood Estimation,MLE)是统计学中常用的参数估计方法,用于根据已观测到的样本数据,选择使得观测数据出现概率最大的参数值。
- 对于离散型随机变量,似然函数是概率质量函数的乘积:
L ( θ ) = P ( X = x 1 ) × P ( X = x 2 ) × ⋯ × P ( X = x n ) L(\theta)=P(X=x_1)\times P(X=x_2)\times \cdots \times P(X=x_n) L(θ)=P(X=x1)×P(X=x2)×⋯×P(X=xn)
- 对于连续型随机变量,似然函数是概率密度函数的乘积:
L ( θ ) = f ( x 1 ∣ θ ) × f ( x 2 ∣ θ ) × ⋯ × f ( x n ∣ θ ) L(\theta)=f(x_1|\theta)\times f(x_2|\theta)\times \cdots \times f(x_n|\theta) L(θ)=f(x1∣θ)×f(x2∣θ)×⋯×f(xn∣θ)
最大似然估计的目标是找到使得似然函数最大化的参数值。
概率、似然
1、概率(发生前推测)
- 某件事情发生的可能性,在结果没有产生之前依据环境所对应的参数来预测某件事情发生的可能性
- 例如抛硬币之前,推测正面朝上的概率为50%
2、似然(发生后推测,参数)
- 是在确定的结果之后推测产生这个结果的可能环境(参数)
- 例如抛一枚硬币1000次,其中500次正面朝上,推测这是一枚标准硬币,正面吵上的概率为50%
统计学两大学派
1、频率学派
- 认为样本信息来自总体,通过对样本信息的研究可以合理地推断、估计总体信息,并且随着样本的增加,推断结果更加准确
- 极大似然估计
2、贝叶斯学派
- 将先验信息和后验信息相结合,通过贝叶斯公式将先验信息与样本数据结合起来,得到后验分布,并以此作为对未知参数的推断(先验分布具有主观性)
相关文章:

【AI算法岗面试八股面经【超全整理】——概率论】
AI算法岗面试八股面经【超全整理】 概率论信息论机器学习CVNLP 目录 1、古典概型、几何概型2、条件概率、全概率公式、贝叶斯公式3、先验概率、后验概率4、离散型随机变量的常见分布5、连续型随机变量的常见分别6、数学期望、方差7、协方差、相关系数8、独立、互斥、不相关9.大…...
vue3 使用vant
使用前提: vite创建的vue3项目 vanthttps://vant-ui.github.io/vant/#/zh-CN/home npm i vant 引入样式: main.js import vant/lib/index.css vant封装 import { showLoadingToast,closeToast,showDialog,showConfirmDialog } from vant;export func…...

网络请求客户端WebClient的使用
在 Spring 5 之前,如果我们想要调用其他系统提供的 HTTP 服务,通常可以使用 Spring 提供的 RestTemplate 来访问,不过由于 RestTemplate 是 Spring 3 中引入的同步阻塞式 HTTP 客户端,因此存在一定性能瓶颈。根据 Spring 官方文档…...
unity制作app(9)--拍照 相册 上传照片
1.传输照片(任何较大的数据)都需要扩展服务器的内存空间。 2.还需要base64编码 2.1客户端发送位置的编码 2.2服务器接收部分的代码...
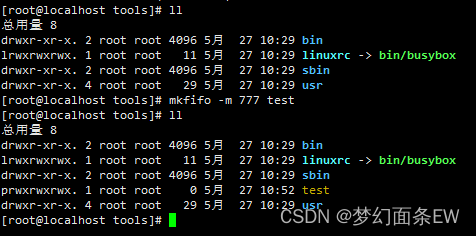
【busybox记录】【shell指令】mkfifo
目录 内容来源: 【GUN】【mkfifo】指令介绍 【busybox】【mkfifo】指令介绍 【linux】【mkfifo】指令介绍 使用示例: 创建管道文件 - 创建的时候同时指定文件权限 常用组合指令: 指令不常用/组合用法还需继续挖掘: 内容来…...

使用Jmeter进行性能测试的基本操作方法
🔥 交流讨论:欢迎加入我们一起学习! 🔥 资源分享:耗时200小时精选的「软件测试」资料包 🔥 教程推荐:火遍全网的《软件测试》教程 📢欢迎点赞 👍 收藏 ⭐留言 …...

Linux学习笔记(epoll,IO多路复用)
Linux learning note 1、epoll的使用场景2、epoll的使用方法和内部原理2.1、创建epoll2.2、使用epoll监听和处理事件 3、示例 1、epoll的使用场景 epoll的英文全称是extend poll,顾名思义是poll的升级版。常见的IO复用技术有select,poll,epo…...

STM32定时器及输出PWM完成呼吸灯
文章目录 一、STM32定时器原理1、基本定时器2、通用定时器(1)时钟源(2)预分频器PSC(3)计数器CNT(4)自动装载寄存器ARR 3、高级定时器 二、PWM工作原理三、控制LED以2s的频率周期性地…...

海外仓管理系统费用解析:如何选择高性价比的海外仓系统
海外仓作为链接国内商家和海外市场的重要环节,其重要性自然是不言而喻的。 对于众多中小型海外仓来说,如何在保证服务质量的同时降低运营成本,就成了大家关注的焦点。今天我们就从海外仓管理系统的费用这个角度,来帮助大家分析一…...

深度学习之学习率调度器Scheduler介绍
调度器是深度学习训练过程中非常重要的一部分,它用于动态调整模型的学习率,从而提高训练效率和最终性能。 1. 为什么需要学习率调度器? 深度学习训练中,学习率是一个非常关键的超参数。合适的学习率可以确保模型快速收敛并获得良好的性能。 但是在训练过程中,最优的学习率会随…...

蓝桥杯-AB路线(详细原创)
问题描述: 有一个由 N M 个方格组成的迷宫,每个方格写有一个字母 A 或者 B。小蓝站在迷宫左上角的方格,目标是走到右下角的方格。他每一步可以移动到上下左右相邻的方格去。 由于特殊的原因,小蓝的路线必须先走 K 个 A 格子、再…...

计算机字符编码的发展
目录 背景 发展 第一阶段:ASCII编码 第二阶段:扩展ASCII编码 第三阶段:各国编码 第四阶段:Unicode编码 第五阶段:UTF系列编码方式 相关扩展 背景 在计算机诞生初期,所有的数据都是基于二进制数&am…...

Java(六)——抽象类与接口
文章目录 抽象类和接口抽象类抽象类的概念抽象类的语法抽象类的特性抽象类的意义 接口接口的概念接口的语法接口的特性接口的使用实现多个接口接口与多态接口间的继承抽象类和接口的区别 抽象类和接口 抽象类 抽象类的概念 Java使用类实例化对象来描述现实生活中的实体&…...

【4.vi编辑器使用(下)】
一、vi编辑器的光标移动 二、vi编辑器查找命令 1、命令::/string 查找字符串 n:继续查找 N:反向继续查找 /^the 查找以the开头的行 /end 查找以 查找以 查找以结尾的行 三、vi编辑器替换命令 1、语法: : s[范围,范围]str1/str2[g] g表示全…...
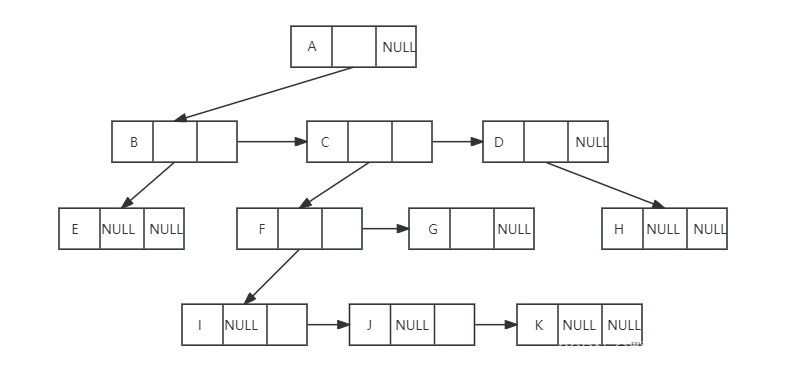
【数据结构】探索树中的奇妙世界
专栏介绍: 哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累…...
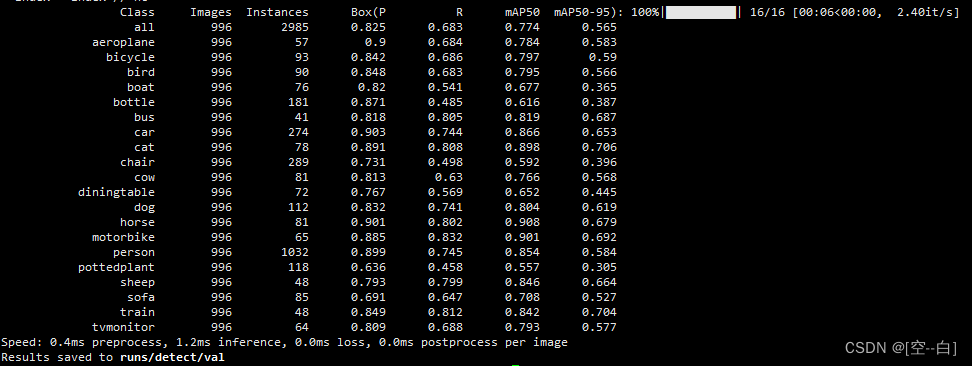
搭建YOLOv10环境 训练+推理+模型评估
文章目录 前言一、环境搭建必要环境1. 创建yolov10虚拟环境2. 下载pytorch (pytorch版本>1.8)3. 下载YOLOv10源码4. 安装所需要的依赖包 二、推理测试1. 将如下代码复制到ultralytics文件夹同级目录下并运行 即可得到推理结果2. 关键参数 三、训练及评估1. 数据结构介绍2. 配…...

c++(一)
c(一) C与C有什么区别命名空间使用 输入输出流引用指针和引用的区别定义拓展 函数重载例子测试函数重载原理 参数默认值什么是参数默认值注意 在c中如何引入c的库动态内存分配new、delete与malloc、free的区别? C与C有什么区别 <1>都是…...

java面试中高频问题----1
一、乐观锁和悲观锁定义、场景怎么判断用什么? 1.乐观锁: 定义:乐观锁假设大多数情况下,资源不会发生冲突。因此,允许多个线程同时访问资源。 场景:读操作多,写操作少,数据冲突概率…...

ABB 控制柜
1,主计算机:相当于电脑的主机,用于存放系统和数据,需要24V直流电才能工作。执行用户编写的程序,控制机器人进行响应的动作。主计算机有很多接口,比如与编程PC连接的服务网口、用于连接示教器的网口、连接轴…...
【错误记录】HarmonyOS 运行报错 ( Failure INSTALL_PARSE_FAILED_USESDK_ERROR )
文章目录 一、报错信息二、问题分析三、解决方案 一、报错信息 在 DevEco Studio 中 , 使用 远程设备 , 向 P40 Failure[INSTALL_PARSE_FAILED_USESDK_ERROR] compileSdkVersion and releaseType of the app do not match the apiVersion and releaseType on the device. 二、…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
