【数据结构】探索树中的奇妙世界
专栏介绍:
哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累。我想让大家知道的是:数据结构非常有趣,很多算法是智慧的结晶,我希望大家在学习数据结构的过程是一种愉悦的心情感受。因此我开创了《数据结构》专栏,在这里我将把数据结构内容以有趣易懂的方式展现给大家。
1.树
1.1树的定义
之前我们一直谈的都是一对一的线性结构,可现实中,还是有很多一对多的情况需要处理,所以我们需要研究这种一对多的数据结构—“树”,考虑它的各种特性,来解决我们在编程中遇到的相关问题。树是一种非线性的数据结构,它是由n(n>=0)个节点组成的一个具有层次关系的集合,把它叫做树是因为它看起来像是一棵倒挂的树,也就是说它根是向上的,叶子是向下的。如下图:
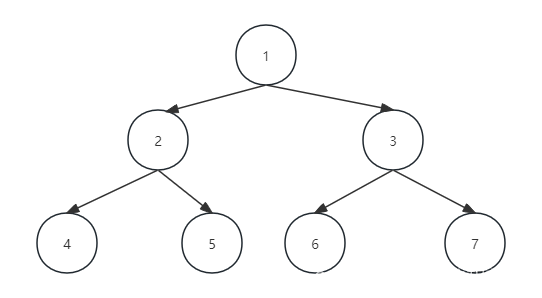
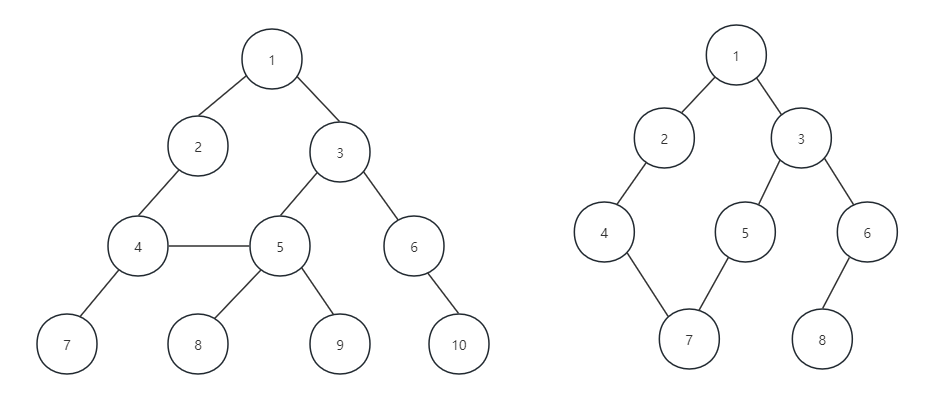
n=0时被称为空树,在任意一棵非空树中:1.有且仅有一个特定的根节点 2.当n>1时,其余节点可以分为m个互不相交的有限集,其中每一个集合本身又都是一个树,被称为子树。如下图:

上面就是两个子树的简单例子,4、5组成的树是以2为根节点的子树,6、7组成的树是以3为结点的子树,对于树的定义还需要强调两点:
- n>0时根节点是唯一的,不可能存在多个根节点,千万不要和现实中的大树混在一起,现实中的树有很多的根须,那时真实的树,数据结构中的树只有一个节点!
- m>0时,子树的个数没有限制,但是他们一定是不相交互的,即同一层次的各个节点之间不相互。像下面展示的结构就不符合树的定义,因为他们之间有交互。
1.2树的相关概念
我们一会就用下面这张图来展开介绍树的相关概念。

- 根节点:根节点是树结构中的第一个节点,也是整个树的起点。它是树的顶部节点。在上面的图中A是这棵树的根节点。一棵树只能有一个根节点。其他节点可以通过根节点进行访问和遍历。根节点是树的分支点,它可以有多个子节点。子节点通过边或链接与根节点相连,形成了树的层次结构。
- 双亲结点/父节点:父节点是树结构中一个节点的上一级节点。每个节点都可以有一个父节点,除了根节点,因为根节点没有父节点。在上图中C就是H的父节点。父节点直接连接到其子节点,形成了树的层次结构。父节点是子节点的直接访问入口。通过父节点,可以找到子节点,进而访问和操作子节点。父节点可以有多个子节点。这使得树结构能够表示复杂的分支关系,每个父节点可以连接到不同的子节点。在上图中F就有3个子节点节点。
- 兄弟节点:兄弟节点是树结构中同一层级的节点之间的关系。它们的父节点是相同的,即它们有相同的父节点。兄弟节点在树的结构中是相邻的,它们在同一层级的位置是相邻的。在上图中K、L、M就互为兄弟节点。
- 祖先节点:从根到该节点所经分支上的所有节点,在上图中A是所有结点的祖先节点。
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙,在上图中所有节点都是A节点的子孙。
- 节点的度:节点的度是指该节点拥有的子节点的数量。在上图中A节点的度为6.
- 叶节点/终端节点:叶节点是指没有子节点的节点,即度为0的节点,在上图中B就是一个叶节点。
- 分支节点:度不为0的节点,除根节点之外,分支节点也叫做内部节点,在上图中C就是一个分支节点。
- 树的度:一棵树中,最大的节点的度称为树的度,上面这张图中树的度为6.
1.3树的存储结构
说到存储结构,我们就会想到之前提到的顺序存储结构和链式存储结构,之前我们都是一对一的结构,现在变成树这样一对多的结构该怎么办呢?在这里我们要充分利用顺序存储和链式存储的特点,来实现对树的存储结构的表示。我们这里要介绍三种不同的表示方法:双亲表示法、孩子表示法、孩子兄弟表示法。
1.3.1双亲表示法
我们有的人可能因为种种原因没有孩子,但无论谁都不可能是从石头缝里蹦出来的。树这种结构也不例外,除了根节点之外,其余每个节点,不一定有子节点,但一定有且仅有一个双亲结点。我们假设以一组连续的空间存储树的节点,同时每个节点中,还要设置一个指针指向双亲结点的位置。也就是说,每个节点除了要知道自己是谁之外,还要知道双亲在哪里,它的结构如下:
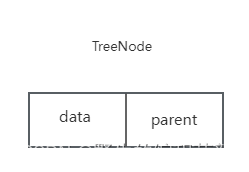
其中,data是数据域,存放节点的数据信息,parent是指针域,存储该节点对应的双亲在数组中的下标 。以下是双亲表示法的节点结构的定义代码:
#define MAX_TREE_SIZE 100
typedef int TNDataType //树结点的数据类型,暂定为整型
typedef struct TreeNode
{TNDataType data;int parent;
}TNode;
typedef struct Tree
{TNode nodes[MAX_TREE_SIZE]; //节点数组int r,n; //根节点的位置和节点数
}Tree;
有了上面的结构定义我们就可以来实现双亲表示法了。由于根节点是没有双亲的,所以我们约定根节点的位置域为-1,这就意味着,我们所有的节点都存在它的双亲的位置。下面图中的树结构可以用双亲表示法来表示:
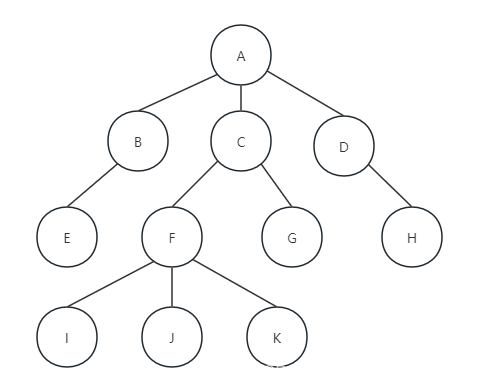
因为按照数组那种连续存储结构画出来的话,图片横向太长不方便看,所以这里我用一个表格来表示方便观看,又简单明了:
| 下标 | data | parent |
| 0 | A | -1 |
| 1 | B | 0 |
| 2 | C | 0 |
| 3 | D | 0 |
| 4 | E | 1 |
| 5 | F | 2 |
| 6 | G | 2 |
| 7 | H | 3 |
| 8 | I | 5 |
| 9 | J | 5 |
| 10 | K | 5 |
这样的存储结构,我们可以根据节点的parent指针很容易的找到它的双亲结点,所用的时间复杂度为O(1),直到parent为-1时,表示找到了树结点的根。可如果我们要知道节点的孩子是什么的话,需要遍历整个数组才行,那我们能否改进一下呢?why not?我们增加一个指针域存放第一个孩子(一般取最左边的子节点)在数组中的下标,这样就很容易得到节点的孩子,如果没有子节点的话,我们就把这个指针域设为-1。如下表表示:
| 下标 | data | parent | firstchild |
| 0 | A | -1 | 1 |
| 1 | B | 0 | 4 |
| 2 | C | 0 | 5 |
| 3 | D | 0 | 7 |
| 4 | E | 1 | -1 |
| 5 | F | 2 | 8 |
| 6 | G | 2 | -1 |
| 7 | H | 3 | -1 |
| 8 | I | 5 | -1 |
| 9 | J | 5 | -1 |
| 10 | K | 5 | -1 |
这样对于有0或1个子节点的的双亲结点来说,这样的结构是为了解决要找子节点的问题,甚至是有多个子节点也能解决,知道了第一个子节点是谁,剩下的子节点也就一目了然了。就像上面表格中A的第一个子节点下标是1,即B节点的位置,而B第一个子节点的下标为4,所以在[1,4)区间中的所有整数在数组中所对应的下标元素就是A的子节点。
这时候又有一个新问题了,我们很关注兄节点之间的关系,双亲表示法无法体验出这种关系,那我们该怎么办呢?这时候我们只需要在双亲表示法的基础上增加一个指针用来指向子结点中最右侧的节点,即右兄弟节点,也就是说每一个节点如果它存在右兄弟,就存放右兄弟的下标,如果右兄弟不在就存放-1,如下表表示:
| 下标 | data | parent | rightbrother |
| 0 | A | -1 | -1 |
| 1 | B | 0 | 2 |
| 2 | C | 0 | 3 |
| 3 | D | 0 | -1 |
| 4 | E | 1 | -1 |
| 5 | F | 2 | 6 |
| 6 | G | 2 | -1 |
| 7 | H | 3 | -1 |
| 8 | I | 5 | 9 |
| 9 | J | 5 | 10 |
| 10 | K | 5 | -1 |
存储结构的设计是一个非常灵活的过程,一个存储结构设计的是否合理,取决于基于该存储结构的运算是否合适、是否方便,时间复杂度好不好等。不是越多越好,有需要时再设计相应的结构,复杂的结构意味着更多的时间和空间的开销,简单的设计对应着快速的查找与删除,我们要根据实际情况进行取舍。
1.3.2孩子表示法
我们换一种思路:由于树中每个节点可能有多个子树,可以考虑使用多重链表,即每个节点有多个指针域,其中每个指针域指向一棵子树的根节点,我们把这种方法叫做多重链表表示法。不过树的每个节点度都是不一样的,所以可以设计两种解决方案。
1.3.2.1方案一
一种方案就是指针域的个数等于树的度,前面我们提到了,树的度是各个节点度的最大值。其结构如下表示:

其中,data就是数据域,child1~childn是指针域,用来指向该节点的孩子节点。在双亲表示法我们提到的那个树用这种方法实现如下图:

这种方法对于树中各个节点的度相差很大,显然是浪费空间的,因为有很多节点,它的指针域是空的。如果树的各个节点的度相差很小的话,那就意味着开辟的空间被充分利用了,这是存储结构的缺点反而成了优点。既然很多指针域为空,为什么不按需求分配空间呢?于是我们有了第二种方案。
1.3.2.2方案二
第二种方案每个结点的指针域等于该节点的度,我们专门取一个位置来存储节点指针域的个数,其结构如下:
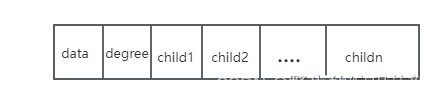
其中,data为数据域,degree为节点的度,也就是存储该节点的子节点的个数,child1~childn为指针域,指向该节点的各个子结点。这种方法实现如下图:
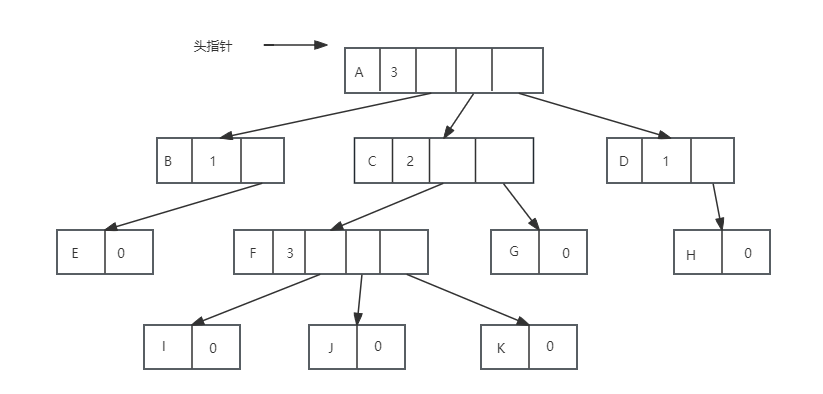
这种方法克服了浪费空间的缺点,对空间的利用率很高了,但是由于各个节点的链表是不相同的结构,加上要维护节点的度的数值,在运算上就会带来时间上的损耗,能否有更好的方法,既可以减少空指针的浪费又能使结点的结构相同。仔细观察,我们为了要遍历整棵树,把每个节点放在一个顺序存储结构的数组中是合理的,但每个结点的孩子有多少是不确定的,所以我们在对每个结点的孩子建立一个单链表体现他们的关系。
这就是我们要讲的孩子表示法。具体办法是:把每个节点的子节点排列起来,以单链表作为存储结构,则n个节点有n个子链表,如果是叶子节点则此单链表为空,然后n个头指针又组成一个线性表,采用顺序存储结构,存放在一个一维数组中。如下图:

为此我们设计两个节点结构,一个是子链表的子节点,如下表表示:

其中,child是数据域,用于存储某个节点在表头数组中的下标;next是指针域,用来存储指向某节点的下一个子节点的指针。另一个是表头数组的表头结点,如下表表示:

其中,data是数据域,存储某节点的数据信息;firstchild是头指针域,存放该节点的子链表的头指针。以下是我们的孩子表示法的结构定义代码:
#define MAX_TREE_SIZE 100
typedef int TNDatatype
typedef struct ChildNode
{int child;struct ChildNode* next;
}CNode;
typedef struct TreeNode
{TNDataType data;CNode* firstchild;
}TNode;
typedef struct Tree
{TNode nodes[MAX_TREE_SIZE];int r,n;
}Tree;这样的结构对于我们要查找某个节点的某个孩子,或者某个节点的兄弟,只需要查找这个节点的子链表即可。对于遍历整棵树也是非常方便的,对头结点的数组循环即可。
1.3.3左孩子右兄弟表示法
刚才我们分别从双亲的角度和孩子的角度研究树的存储结构,如果我们从树节点的兄弟角度考虑会如何呢?当然对于树这样的层级结构来说,之研究节点的兄弟是不行的,我们观察后发现:任何一颗树,他的结点的的第一个孩子如果i存在就是唯一的,同理它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该节点的第一个孩子和它的右兄弟。这个方法我们成为左孩子右兄弟表示法。这个表示法在我们学习二叉树时常用到,是一个非常重要的知识点。节点结构如下:

其中,data是数据域,firstchild为指针域,存放该节点的第子节点的存储地址,rightbrother也是指针域,存储该节点的右兄弟节点的存储地址,结构定义代码如下:
typedef struct TreeNode
{TNDataType data;struct TreeNode* firstchild;struct TreeNode* rightbrother;
}TNode;对于上面的树来说,这种实现方法示意图如下:
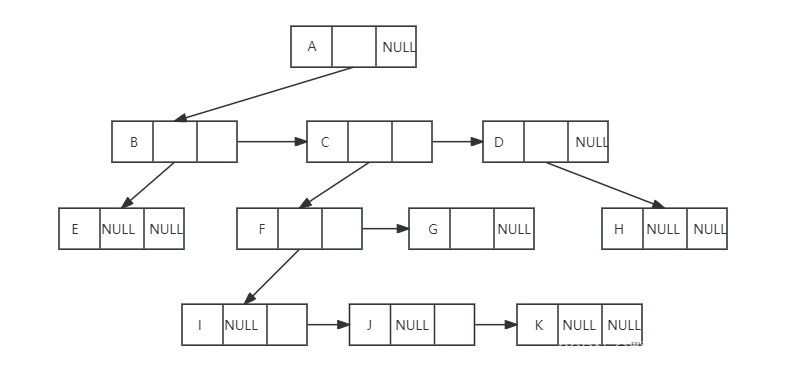
这种表示法,给查找某个节点的某个孩子带来了方便,只需要通过firstchild找到此节点的第一个孩子,然后再通过第一个子节点的rightbrother找到他的兄弟,按照这样一直下去,直到找到具体的孩子。其实这个表示法的最大好处就是把他从一棵复杂的树变成了一棵二叉树。在下一篇再详细介绍二叉树。
相关文章:

【数据结构】探索树中的奇妙世界
专栏介绍: 哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累…...
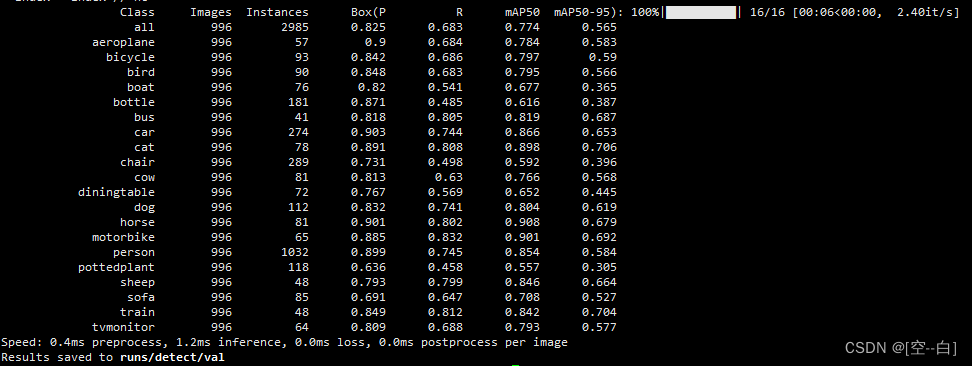
搭建YOLOv10环境 训练+推理+模型评估
文章目录 前言一、环境搭建必要环境1. 创建yolov10虚拟环境2. 下载pytorch (pytorch版本>1.8)3. 下载YOLOv10源码4. 安装所需要的依赖包 二、推理测试1. 将如下代码复制到ultralytics文件夹同级目录下并运行 即可得到推理结果2. 关键参数 三、训练及评估1. 数据结构介绍2. 配…...

c++(一)
c(一) C与C有什么区别命名空间使用 输入输出流引用指针和引用的区别定义拓展 函数重载例子测试函数重载原理 参数默认值什么是参数默认值注意 在c中如何引入c的库动态内存分配new、delete与malloc、free的区别? C与C有什么区别 <1>都是…...

java面试中高频问题----1
一、乐观锁和悲观锁定义、场景怎么判断用什么? 1.乐观锁: 定义:乐观锁假设大多数情况下,资源不会发生冲突。因此,允许多个线程同时访问资源。 场景:读操作多,写操作少,数据冲突概率…...

ABB 控制柜
1,主计算机:相当于电脑的主机,用于存放系统和数据,需要24V直流电才能工作。执行用户编写的程序,控制机器人进行响应的动作。主计算机有很多接口,比如与编程PC连接的服务网口、用于连接示教器的网口、连接轴…...
【错误记录】HarmonyOS 运行报错 ( Failure INSTALL_PARSE_FAILED_USESDK_ERROR )
文章目录 一、报错信息二、问题分析三、解决方案 一、报错信息 在 DevEco Studio 中 , 使用 远程设备 , 向 P40 Failure[INSTALL_PARSE_FAILED_USESDK_ERROR] compileSdkVersion and releaseType of the app do not match the apiVersion and releaseType on the device. 二、…...

使用C语言openssl库实现 RSA加密 和 消息验证
Q:什么是RSA? A:RSA(Rivest-Shamir-Adleman)是一种非对称加密算法,是最早的一种用于公开密钥加密和数字签名的算法。它使用一对公钥(public key)和私钥(private key&…...

海外投放面试手册
海外投放面试手册 岗位职责: 负责Google 、Facebook、TikTok、Twitter等海外主流广告平台的自主投放操作及合作渠道沟通;负责海外合作渠道媒体的广告投放管理、媒体数据监测、效果分析、优化调整等工作; 3.了解海外各渠道&…...
第十三章 进程与线程
第十三章 进程与线程 程序与进程的概念 程序: 英文单词为Program,是指一系列有序指令的集合,使用编程语言所编写,用于实现一定的功能。 进程: 进程则是指启动后的程序,系统会为进程分配内存空间。 函数式…...
、状态后端选择和调优等有所了解)
Flink面试整理-对Flink的高级特性如CEP(复杂事件处理)、状态后端选择和调优等有所了解
Apache Flink 提供了一系列高级特性,使其成为一个强大的实时数据处理框架,特别适用于复杂的数据处理场景。其中,复杂事件处理(CEP)、状态后端的选择和调优是其中重要的几个方面。 复杂事件处理(CEP) CEP 概念:CEP 是用于在数据流中识别复杂模式的技术。它允许用户指定事…...

算法:树状数组
文章目录 面试题 10.10. 数字流的秩327. 区间和的个数315. 计算右侧小于当前元素的个数 树状数组可以理解一种数的存储格式。 面试题 10.10. 数字流的秩 假设你正在读取一串整数。每隔一段时间,你希望能找出数字 x 的秩(小于或等于 x 的值的个数)。 请实现数据结构…...

Kafka SASL_SSL集群认证
背景 公司需要对kafka环境进行安全验证,目前考虑到的方案有Kerberos和SSL和SASL_SSL,最终考虑到安全和功能的丰富度,我们最终选择了SASL_SSL方案。处于知识积累的角度,记录一下kafka SASL_SSL安装部署的步骤。 机器规划 目前测试环境公搭建了三台kafka主机服务,现在将详…...
同城交友论坛静态页面app Hbuild
关注...

spring session+redis存储session,实现用户登录功能,并在拦截器里面判断用户session是否过期,过期就跳转到登录页面
在Spring应用中,使用Redis存储Session是一种常见的方式,可以实现分布式环境下的Session管理。以下是实现用户登录功能,并在拦截器中判断Session是否过期并跳转到登录页面的基本步骤: 添加依赖:首先,确保你的…...

Debug-013-el-loading中显示倒计时时间
前言: 今天实现一个小小的优化,业务上是后端需要从设备上拿数据,所以前端需要不断调用一个查询接口,直到后端数据获取完毕,前后端根据一个ending字段为true判断停止调用查询接口。由于这个查询时间比较久&…...

5月29日,每日信息差
第一、据悉,微信视频号直播电商团队将并入到微信开放平台(小程序、公众号等)团队,原微信视频号直播电商团队转由微信开放平台负责人负责。知情人士表示,此次调整,将有助于微信视频号直播电商业务更好地融入…...

2024年弘连网络FIC大会竞赛题线下决赛题
总结: FIC决赛的时候,很多小问题没发现,在pve平台做题确实很方便。 这套题目复盘完,服务器这块的知识确实收获了很多,对pve集群平台和网络拓扑也有了一定的认识,感谢各位大佬悉心指导。 接下来࿰…...

Element-UI 入门指南:从安装到自定义主题的详细教程
Element-UI 是一个基于 Vue.js 的前端组件库,它提供了丰富的 UI 组件,可以帮助开发者快速构建高质量的用户界面。以下是使用 Element-UI 的快速入门指南: 安装 Element-UI Element-UI 是一个基于 Vue.js 的组件库,它提供了丰富的…...
vs工程添加自定义宏
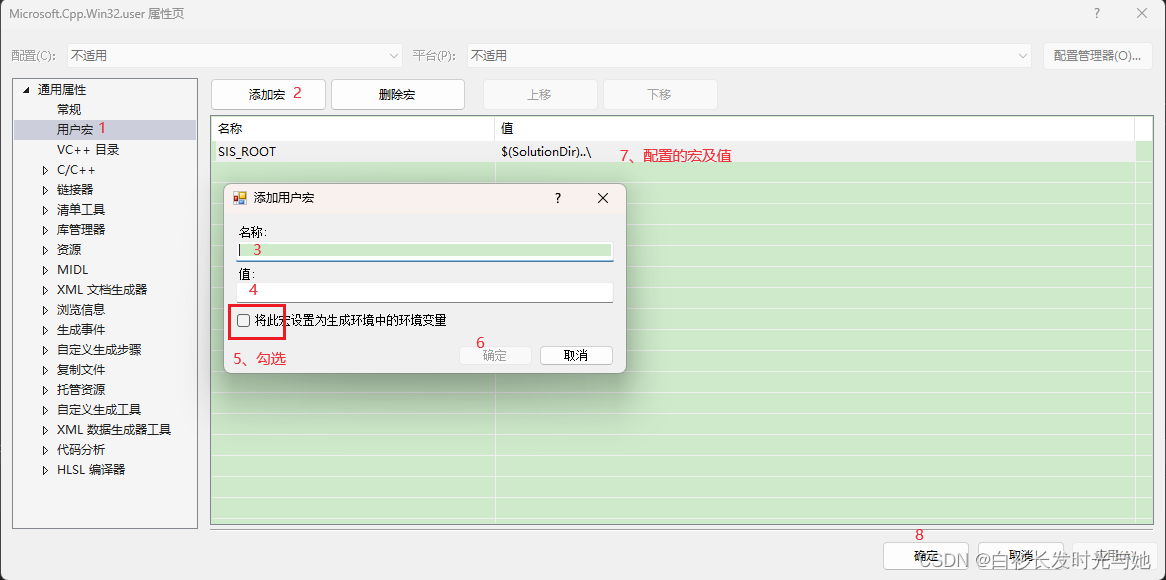
一、简介 用户可以添加自定义宏变量方便工程路径名称的修改和配置 例:$(SolutionDir) 为解决方案路径,$(PojectDir) 为工程所在路径 测试环境:vs2017,qt5.14.0 二、配置 1、打开属性窗口:视图-》其他窗口-》属性管…...

shell脚本:将一维数组以二维数组显示
shell脚本:将一维数组改成二维数组显示 1.编辑脚本文件 vi output_array.sh2.编写脚本 #!/bin/bash# 假设一维数组one_array已经包含9个元素 one_array(1 2 3 4 5 6 7 8 9) # 获取数组长度 length${#one_array[]} # 数组长度除以3获得新数组行数n n$((length / …...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
