【C++】---二叉搜索树
【C++】---二叉搜索树
- 一、二叉搜索树概念
- 二、二叉搜索树操作(非递归)
- 1.二叉搜索树的查找 (非递归)
- (1)查找
- (2)中序遍历
- 2.二叉搜索树的插入(非递归)
- 3.二叉搜索树的删除(非递归)
- 三、二叉搜索树操作(递归)
- 1.二叉搜索树的查找(递归)
- 2.二叉搜索树的插入(递归)
- 3.二叉搜索树的删除(递归)
- 四、二叉搜索树的默认成员函数
- 1.构造
- 2.拷贝构造
- 3.赋值运算符重载
- 4.析构
- 五、K模型和KV模型搜索树
- 1.K模型搜索树
- 2.KV模型搜索树
- 六、二叉搜索树性能分析

一、二叉搜索树概念
二叉搜索树又叫二叉排序数,它或者是空树,或者是具有以下性质的二叉树:
- 如果它的左子树不为空,那么左子树上所有节点的值都小于根结点的值。
- 如果它的右子树不为空,那么右子树上所有节点的值都大于根节点的值。
- 它的左右子树也是二叉搜索树。

int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
比如说:这个数组都可以将它化为二叉搜索树
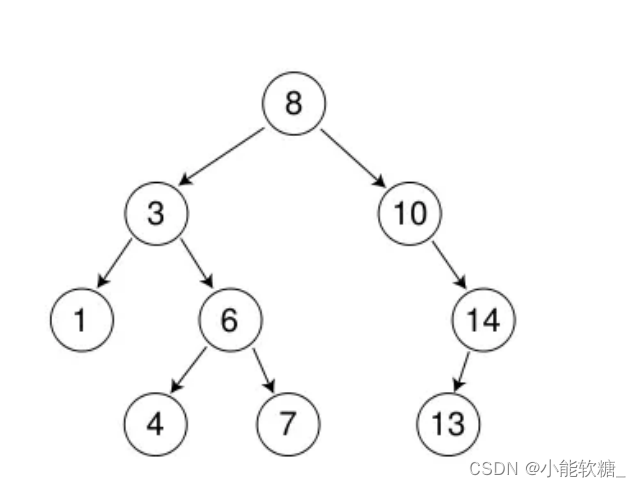
总结:在左子树值比根小,右子树值比根大。 当树走中序遍历时,序列都是有序的。
二叉搜索树 的 结构定义:
#include<iostream>
using namespace std;template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
private:Node* _root;
public:BSTree():_root(nullptr){}
};
二、二叉搜索树操作(非递归)
1.二叉搜索树的查找 (非递归)
利用二分查找的方法,借助我们去二叉搜索树中查找节点。
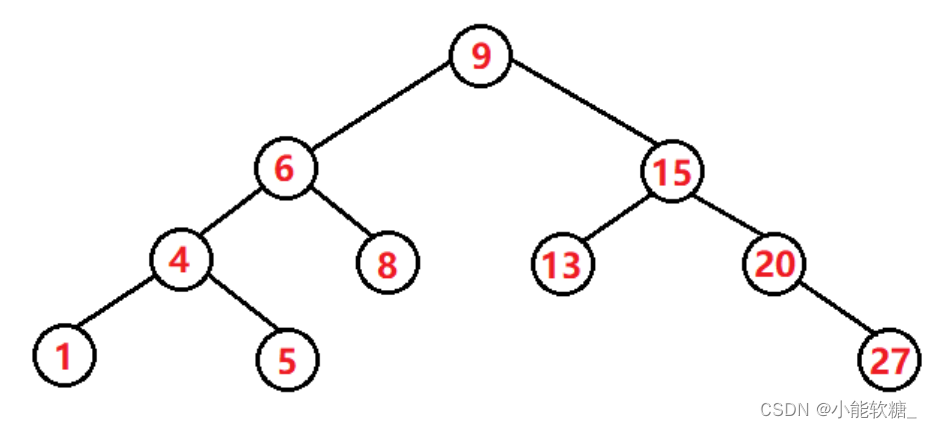

查找的时间复杂度:最坏的情况,就是查找高度(h=logN)次,就可以判断一个值在不在节点里面。
(1)查找
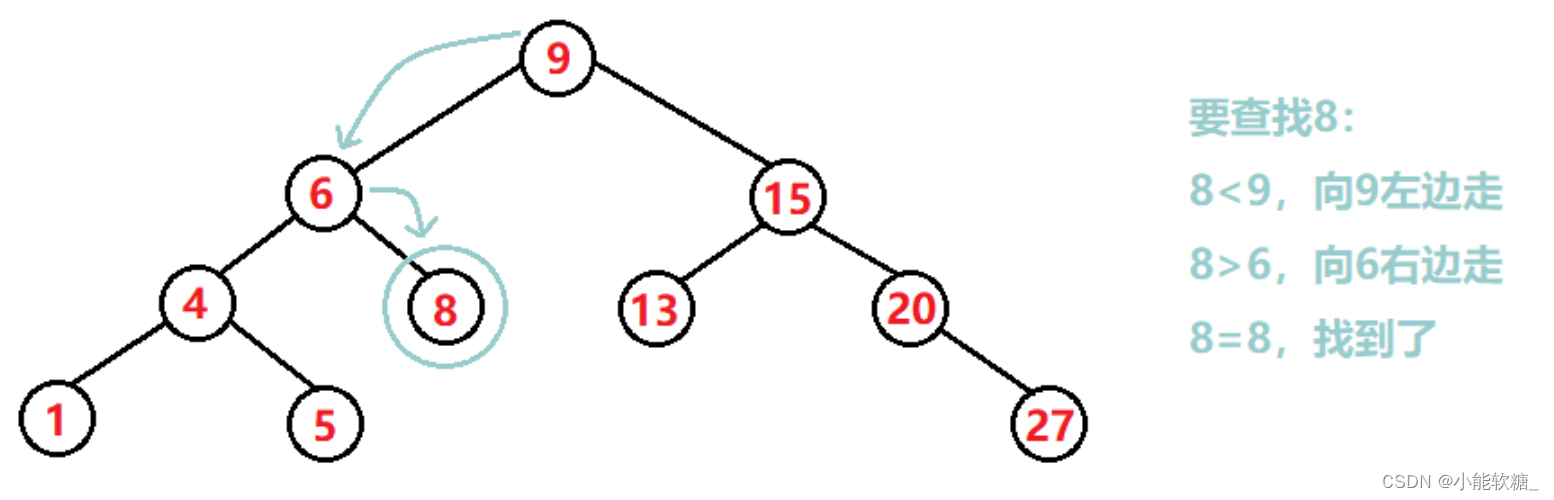
查找的思路:
- key比当前结点的值小,往左走!
- key比当前结点的值大,往右走!
- key==当前结点的值,就找到了!
// 查找:Node* Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return cur;// 找到了!}}return nullptr;// 遍历完了,都还没找到!}
(2)中序遍历
由于根节点_root是私有成员变量,如果在main函数里面来进行中序遍历的话,这就是在类外对私有成员进行访问,这是不合法的!
所以说我们要解决这个问题,可以用这样:
在类的public内的 中序遍历 InOrder 里面 再套一层私有的中序遍历:_InOrder,这样,_InOrder身为私有函数,就可以访问:私有变量_root!
private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << endl;_InOrder(root->_right);}
public:// 中序遍历:void InOrder() //这个函数 类外可以直接访问!{_InOrder(_root); // 这个函数,是 私有函数 对 私有成员 的访问!cout << endl;}
2.二叉搜索树的插入(非递归)
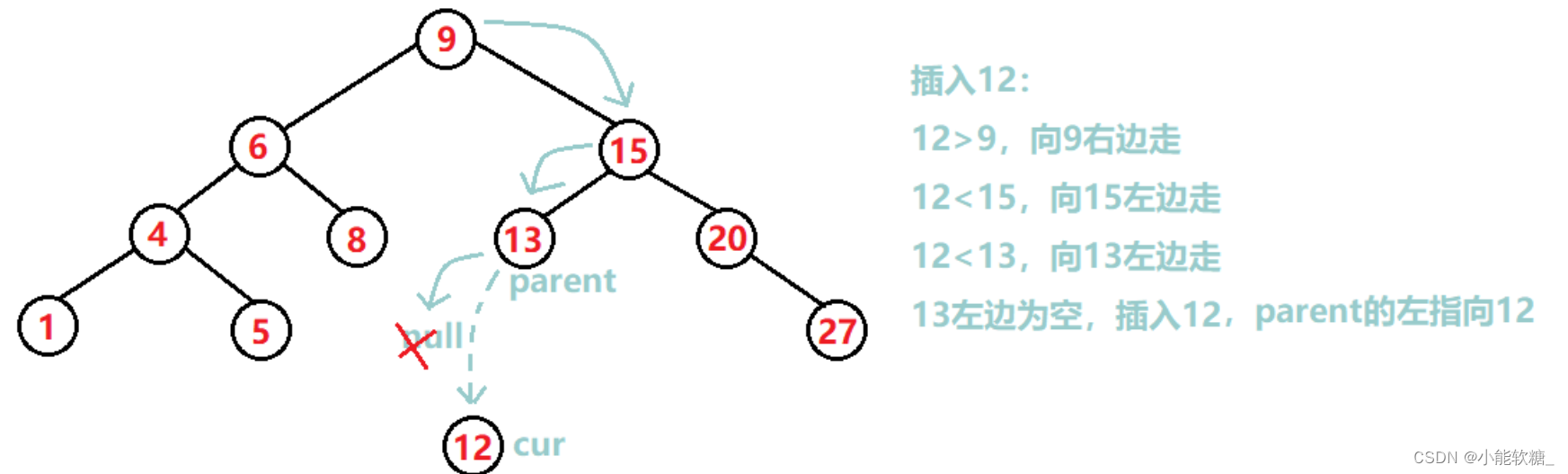
插入节点分两步:
(1)找位置
①key比当前节点值大,向左走②key比当前节点值小,向右走③key等于当前节点值,该节点值已经存在,插入失败
(2)插入
①key比父亲节点值小就插入父亲左子树②key比父亲节点值大就插入父亲右子树
由于插入后,要将节点链接到树中,因此要定义parent节点,用来链接新节点:
// 插入:bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;// (1) 找到插入的位置while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;// 二叉搜索树不允许数据冗余!}}cur = new Node(key);// (2) 判断if (key<parent->_key){parent->_left = cur;}else{parent->_right = cur;}return true;}
3.二叉搜索树的删除(非递归)
非递归删除:
(1)找位置
①key比当前节点值大,向左走②key比当前节点值小,向右走③key等于当前节点值,找到了,准备删除
(2)删除,有两种删除方法:非递归和递归
非递归删除: ①该节点没有孩子,即该节点是叶子节点,删除节点后把父亲指向自己的指针置空
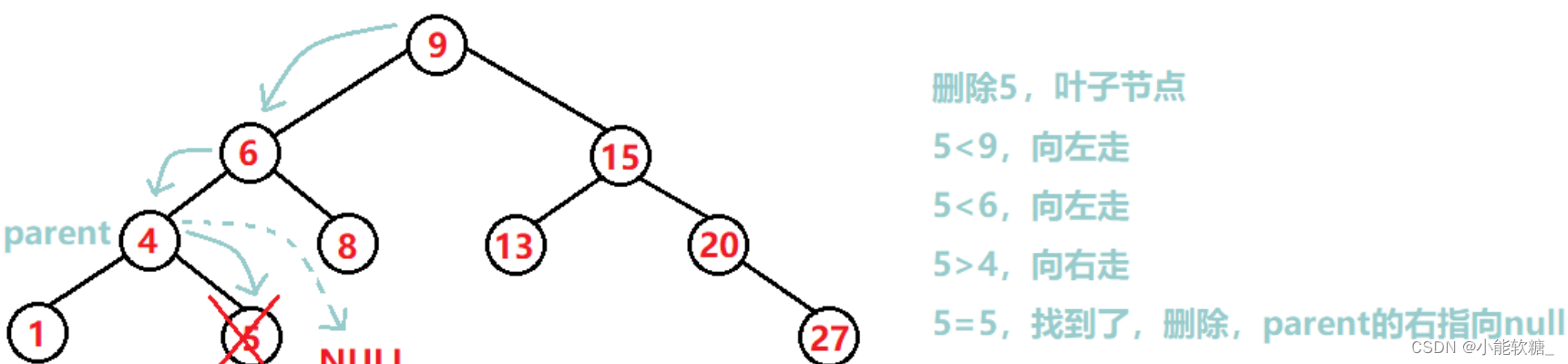
②该节点有一个孩子,就把该节点的孩子节点的链接给该节点的父亲,顶替自己的位置,①可以当成②的特殊情况
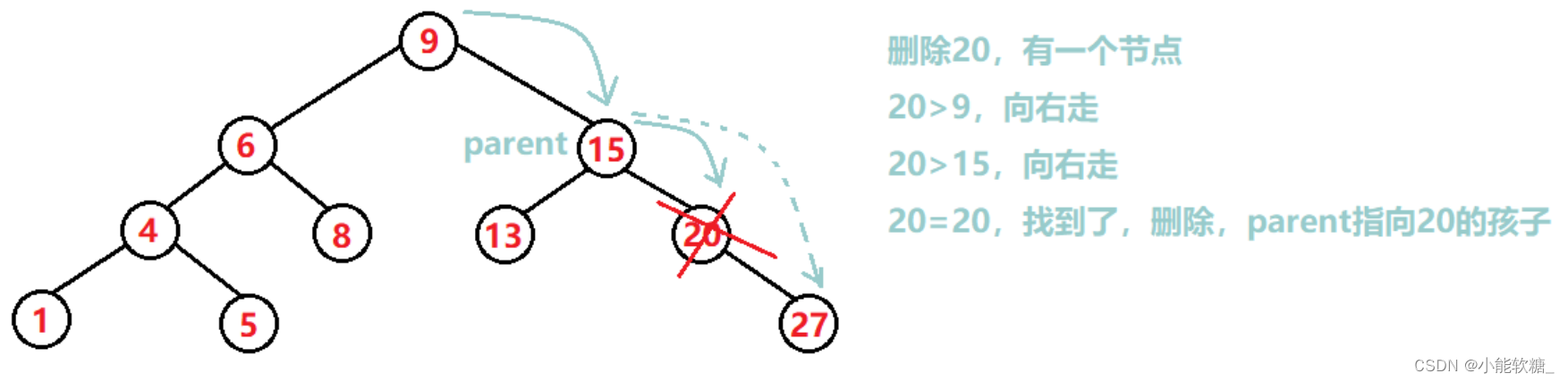
③该节点有两个孩子,找比它自己的左孩子大,比它自己的右孩子小的节点替换它(也就是拿它的左子树的最大节点或右子树的最小节点替换它),替换之后,该节点就只有一个孩子或没有孩子了,就变成①或②了。
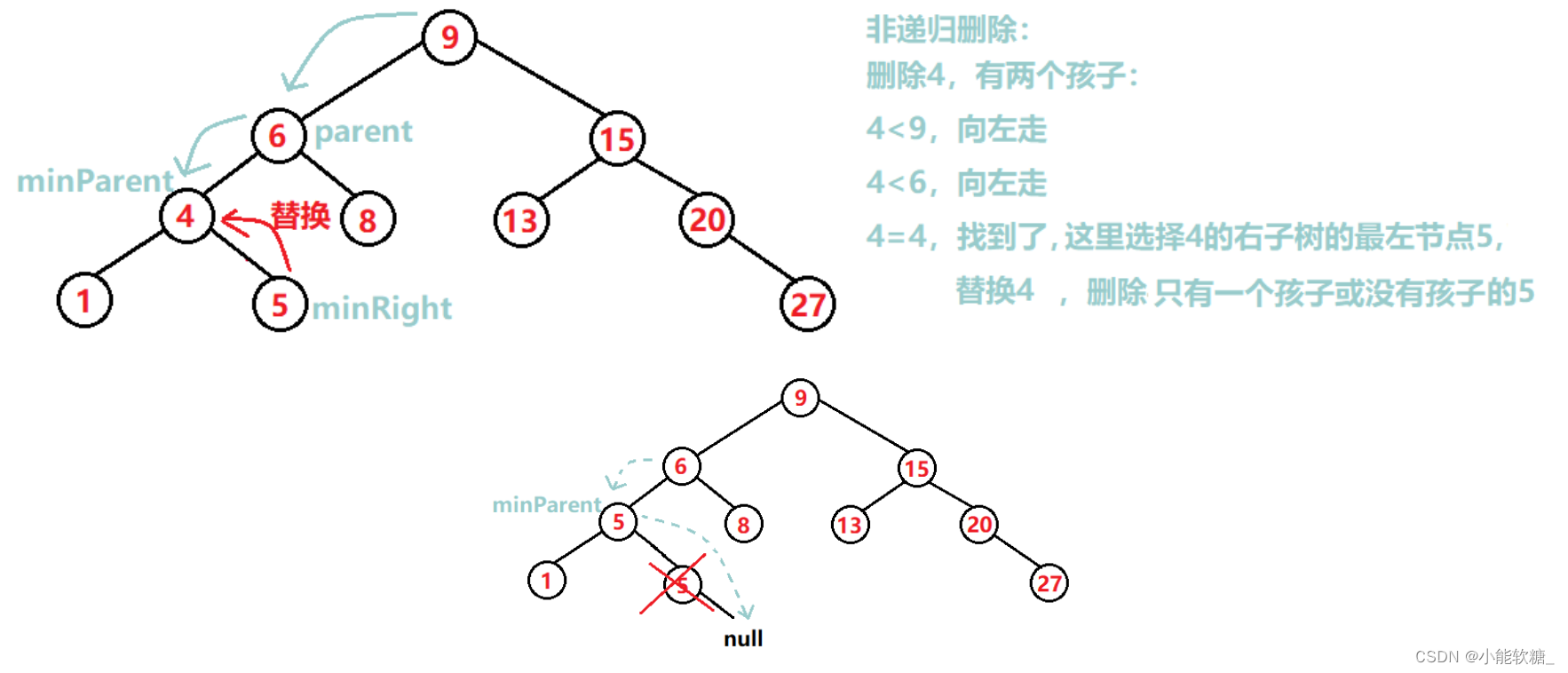
// 删除bool erase(const K& key){Node* cur = _root;Node* parent = nullptr;// (1) 找到插入的位置while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{break;}}// 1、2、 (子 代替 父亲的位置)// 大前提:如果要删除的节点,left为空if (cur->_left == nullptr){// 如果要删除根!if (cur == _root){_root = cur->_right;// 那就让cur的右当根}// 如果要删除的不是根!else{// 如果要删除的节点cur,在父亲的左边。// 因为是替代法,所以说要让 子 的位置代替 父亲 的位置,但是 子 的位置只有_right存在,所以说会把_right的位置放到即将要删除cur的位置。if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}// 大前提:如果要删除的节点,right为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{// 因为是替代法,所以说要让 子 的位置代替 父亲 的位置,但是 子 的位置只有_left存在,所以说会把_left的位置放到即将要删除cur的位置。if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}// 3、要删除的cur不只有一个节点。可能有多个节点,甚至整个指子树// 找到要删除节点cur,左子树最大的节点,右子树最小的节点,来代替cur的位置。else{// 要么找cur左子树中的max,要么就找右子树中的min// 这里 以 RightMin为例!// (1)找到 RightMin (就像找 cur那样)Node* RightMin = cur->_right;Node* RightMinParent = cur; // 定义 RightMinParent 为了方便后续节点的连接。while (RightMin->_left){RightMinParent = RightMin;RightMin = RightMin->_left;}// (2)找到了 就交换!swap(RightMin->_key, cur->_key);// (3) 交换完后 就链接!if (RightMinParent->_left == RightMin)RightMinParent->_left = cur;elseRightMinParent->_right = cur;// 链接完成!delete cur;}return true;}
递归删除:
相对于非递归,只需要修改找到了要修改的代码:找到了后不需要管cur到底左为空、右为空、还是左右都不为空
① 找要删除节点的右子树的最小节点并把它的值保存起来
② 删除右子树的最小节点
③ 把要删除的节点值替换成右子树的最小节点值
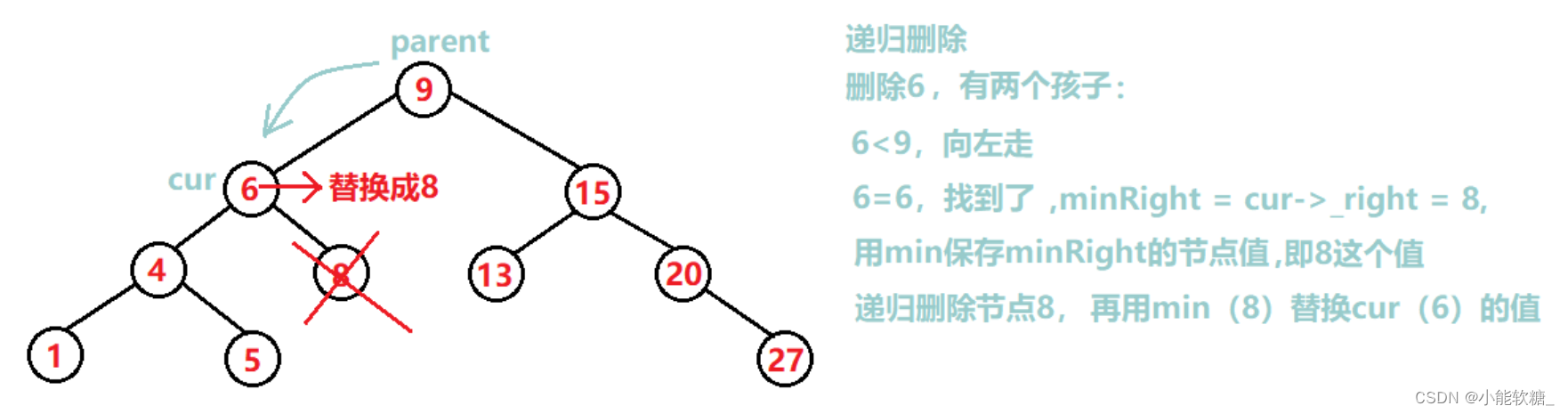
else//左右都不为空,替换法删除{//找右子树最小节点Node* minRight = cur->_right;while (minRight->_left){minRight = minRight->_left;}//用min保存右子树最小节点的值K min = minRight->_key;//递归调用自己去替换删除节点,一定会走到左为空的情况处理this->Erase(min);//删除完毕替换节点之后,把cur的值替换成mincur->_key = min;}
三、二叉搜索树操作(递归)
理解了非递归操作以后, 递归操作就很简单了:
#include<iostream>
using namespace std;//树的节点可以支持多种类型
template<class K>
//树节点结构
struct BSTreeNode
{BSTreeNode<K>* _left;//左指针BSTreeNode<K>* _right;//右指针K _key;//值//构造函数BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template<class K>
class BStree//树结构
{typedef BSTreeNode<K> Node;
public://递归查找Node* FindR(const K& key){return _FindR(_root, key);}//递归插入bool InsertR(const K& key){return _InsertR(_root, key);}//递归删除bool EraseR(const K& key){return _EraseR(_root, key);}
private:Node* _root;
};
由于_root是私有的,可以把递归子函数查找、插入、删除都定义成私有的
1.二叉搜索树的查找(递归)
private://查找Node* _FindR(Node* root, const K& key){if (root == nullptr)//没找到{return nullptr;}if (key < root->_key)//到左子树去找{FindR(root->_left, key);}else if (key > root->_key)//到右子树去找{FindR(root->_right, key);}else//找到了{return root;}}
2.二叉搜索树的插入(递归)
//插入 加了&,root是_root的别名,修改root就直接修改到上一层调用,不用找父亲bool _InsertR(Node*& root, const K& key){if (root == nullptr)//找到位置了{root = new Node(key);return true;}if (key < root->_key)//到左子树去找位置{_InsertR(root->_left, key);}else if (key > root->_key)//到右子树去找位置{_InsertR(root->_right, key);}else//已存在,无需插入{return false;}}
3.二叉搜索树的删除(递归)
递归删除:和二叉树的删除(非递归)一样,找到后的删除也有两种方式,递归和非递归
找到后的非递归删除:
//插入 加了&,root是_root的别名,修改root就直接修改到上一层调用,不用找父亲 bool _EraseR(Node*& root, const K& key){if (root == nullptr)//没找到{return false;}if (key < root->_key)//到左子树去找{_EraseR(root->_left, key);}else if (key > root->_key)//到右子树去找{_EraseR(root->_right, key);}else{//找到了,root就是要删除的节点if (root->_left == nullptr)//root左为空{Node* del = root;root = root->_right;delete del;}else if (root->_right == nullptr)//root右为空{Node* del = root;root = root->_left;delete del;}else//root左右都不为空{//找到右子树最左节点替换Node* minParent = root;Node* minRight = root->_right;while (minRight->_left){minParent = minRight;minRight = minRight->_left;}//保存替换节点的值cur->_key = minRight->_key;//链接if (minParent->_left == minRight){minParent->_left = minRight->_right;}else{minParent->_right = minRight->_right;}//删除delete minRight;}return true;}}
找到后的递归删除:
else//root左右都不为空{ //找右子树最左节点Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}//保存右子树最左节点的值K min = minRight->_key;//使用递归方法删除右子树最左节点_Erase(root->_right, min);}
四、二叉搜索树的默认成员函数
现在还剩下二叉搜索树的构造、拷贝构造、赋值运算符重载、析构函数。
1.构造
public://构造函数需要将根初始化为空就行了BSTree():_root(nullptr){}
2.拷贝构造
拷贝构造利用递归调用子函数不断拷贝节点:
//拷贝构造BSTree(const BSTree<K>& t){_root = t.copy(t._root);}
在子函数处:
Node* _copy(Node* root){if (root == nullptr)//如果根为空,直接返回{return;}Node* copyNode = new Node(root->_key);//创建根节点copyNode->_left = _copy(root->_left);//递归拷贝左子树节点copyNode->_right = _copy(root->_right);//递归拷贝右子树节点return copyNode;//返回根}
3.赋值运算符重载
借助拷贝构造用现代写法写:
//赋值运算符重载(现代写法)BSTree& operator=(const BSTree<K>& t){swap(_root,t._root);return *this;}
4.析构
递归调用子函数去析构
//析构~BSTree(){_Destroy(_root);_root = nullptr;}
在子函数处:
_Destroy(root){if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;}
五、K模型和KV模型搜索树
1.K模型搜索树
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
1、以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
2、在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2.KV模型搜索树
KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:
1、比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
2、再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出
现次数就是<word, count>就构成一种键值对。
改造二叉搜索树为KV结构的代码
#pragma once
#include<iostream>
#include<string>
using namespace std;namespace key_value
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;// pair<K, V> _kv;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:// logNbool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return cur;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 左为空,父亲指向我的右if (cur->_left == nullptr){//if(parent == nullptr)if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//if(parent == nullptr)if (cur == _root){_root = cur->_left;}else{// 右为空,父亲指向我的左if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 左右都不为空,替换法删除// // 查找右子树的最左节点替代删除Node* rightMinParent = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}swap(cur->_key, rightMin->_key);if (rightMinParent->_left == rightMin)rightMinParent->_left = rightMin->_right;elserightMinParent->_right = rightMin->_right;delete rightMin;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};
六、二叉搜索树性能分析
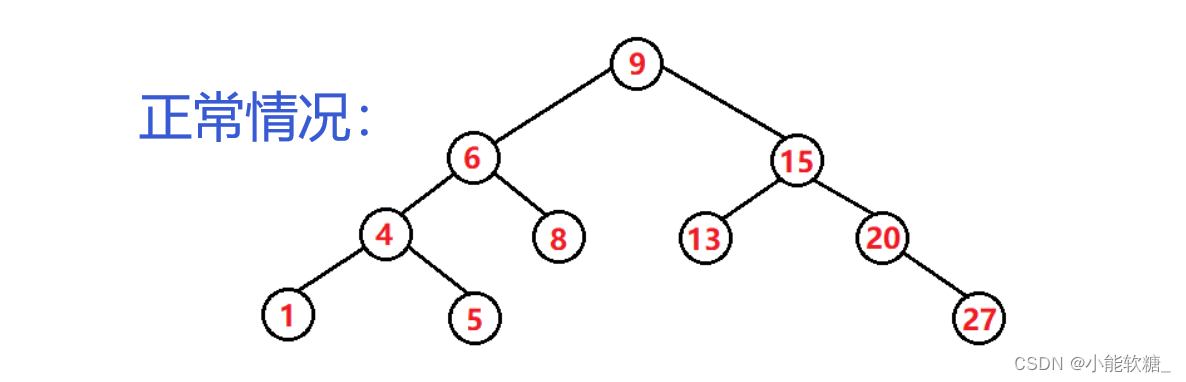
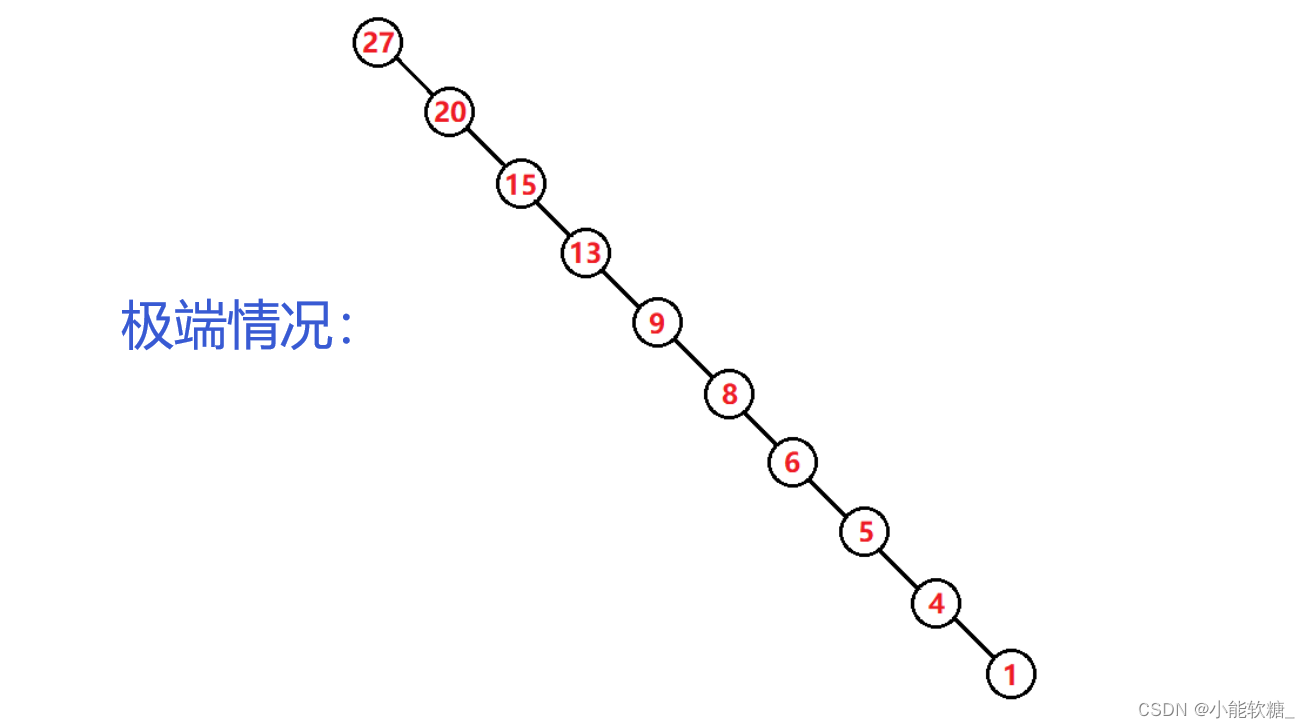

好了,今天的分享就到这里了
如果对你有帮助,记得点赞👍+关注哦!
我的主页还有其他文章,欢迎学习指点。关注我,让我们一起学习,一起成长吧!

相关文章:

【C++】---二叉搜索树
【C】---二叉搜索树 一、二叉搜索树概念二、二叉搜索树操作(非递归)1.二叉搜索树的查找 (非递归)(1)查找(2)中序遍历 2.二叉搜索树的插入(非递归)3.二叉搜索树…...

FastAPI - 依赖注入3
在FastAPI中,依赖注入是一种强大的功能,它允许你轻松地将依赖项注入到你的路由处理程序函数中,以处理不同的任务,例如数据库访问、认证和配置管理。 FastAPI支持依赖注入通过以下方式: 使用参数注解: 你可…...

【网络运维的重要性】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...
YOLOv5改进 | 注意力机制 | 添加双重注意力机制 DoubleAttention【附代码/涨点能手】
💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 在图像识别中,学习捕捉长距离关系是基础。现有的CNN模型通常通过增加深度来建立这种关系,但这种形式效率极低。因此&…...

自用网站合集
总览 线上工具-图片压缩 TinyPNG线上工具-url参数解析 线上工具-MOV转GIF UI-Vant微信小程序版本其他-敏捷开发工具 Leangoo领歌 工具 线上工具-图片压缩 TinyPNG 不能超过5m,别的没啥缺点 线上工具-url参数解析 我基本上只用url参数解析一些常用的操作在线…...

【Golang】gin框架如何在中间件中捕获响应并修改后返回
【Golang】gin框架如何在中间件中捕获响应并修改后返回 本文讲述如何捕获中间件响应以及重写响应如果想在中间件中记录响应日志等操作,我们该如何获取响应数据呢?假如需要统一对响应数据做加密,如何修改这个返回数据再响应给客户端呢…...

电脑同时配置两个版本mysql数据库常见问题
1.配置时,要把bin中的mysql.exe和mysqld.exe 改个名字,不然两个版本会重复,当然,在初始化数据库的时候,如果时57版本的,就用mysql57(已经改名的)和mysqld57 代替 mysql 和 mysqld 例如 mysql -u root -p …...
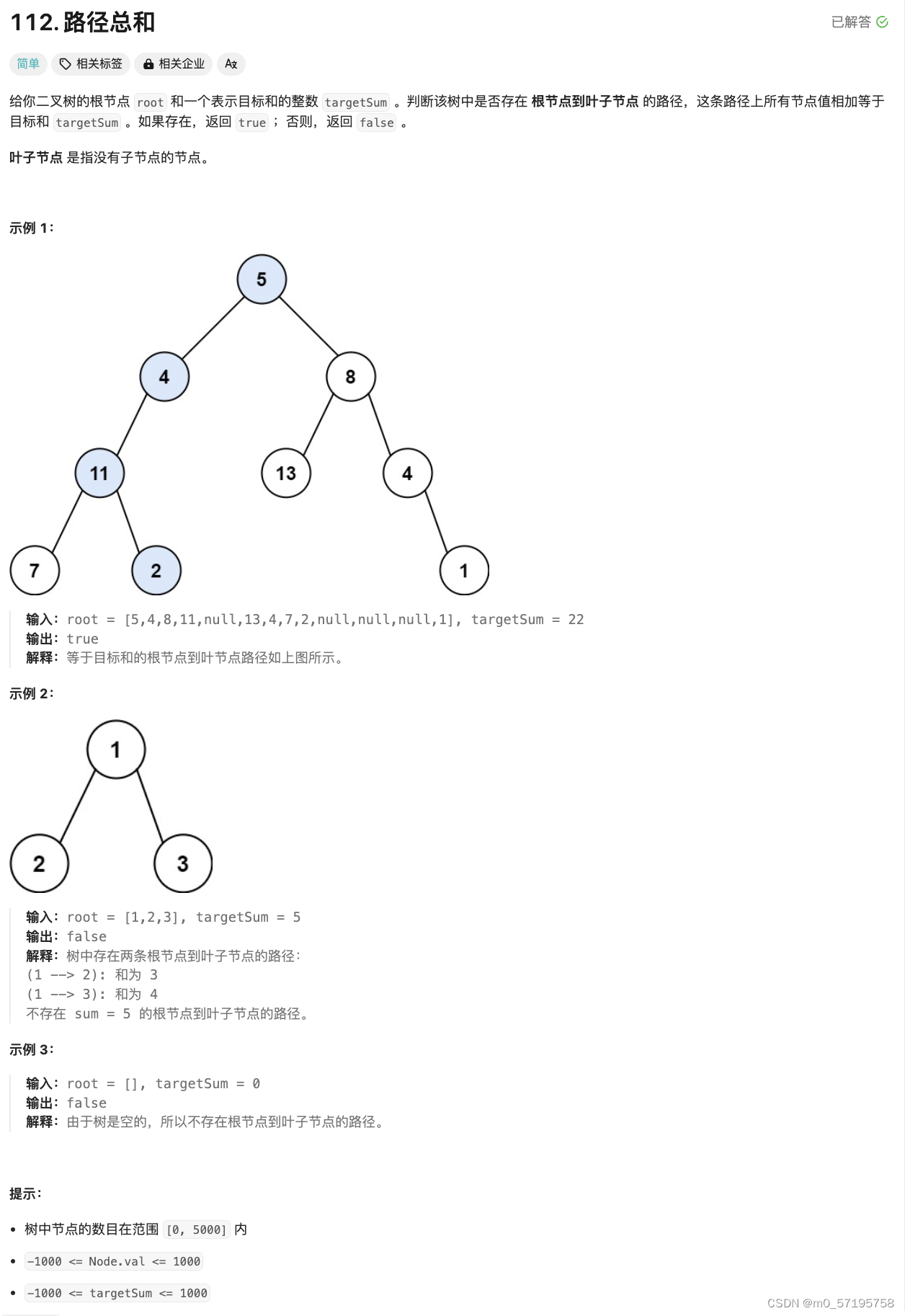
Java | Leetcode Java题解之第112题路径总和
题目: 题解: class Solution {public boolean hasPathSum(TreeNode root, int sum) {if (root null) {return false;}if (root.left null && root.right null) {return sum root.val;}return hasPathSum(root.left, sum - root.val) || has…...
HaloDB 的 Oracle 兼容模式
↑ 关注“少安事务所”公众号,欢迎⭐收藏,不错过精彩内容~ 前倾回顾 前面介绍了“光环”数据库的基本情况和安装办法。 哈喽,国产数据库!Halo DB! 三步走,Halo DB 安装指引 ★ HaloDB是基于原生PG打造的新一代高性能安…...

【Python】解决Python报错:TypeError: ‘xxx‘ object does not support item assignment
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向…...
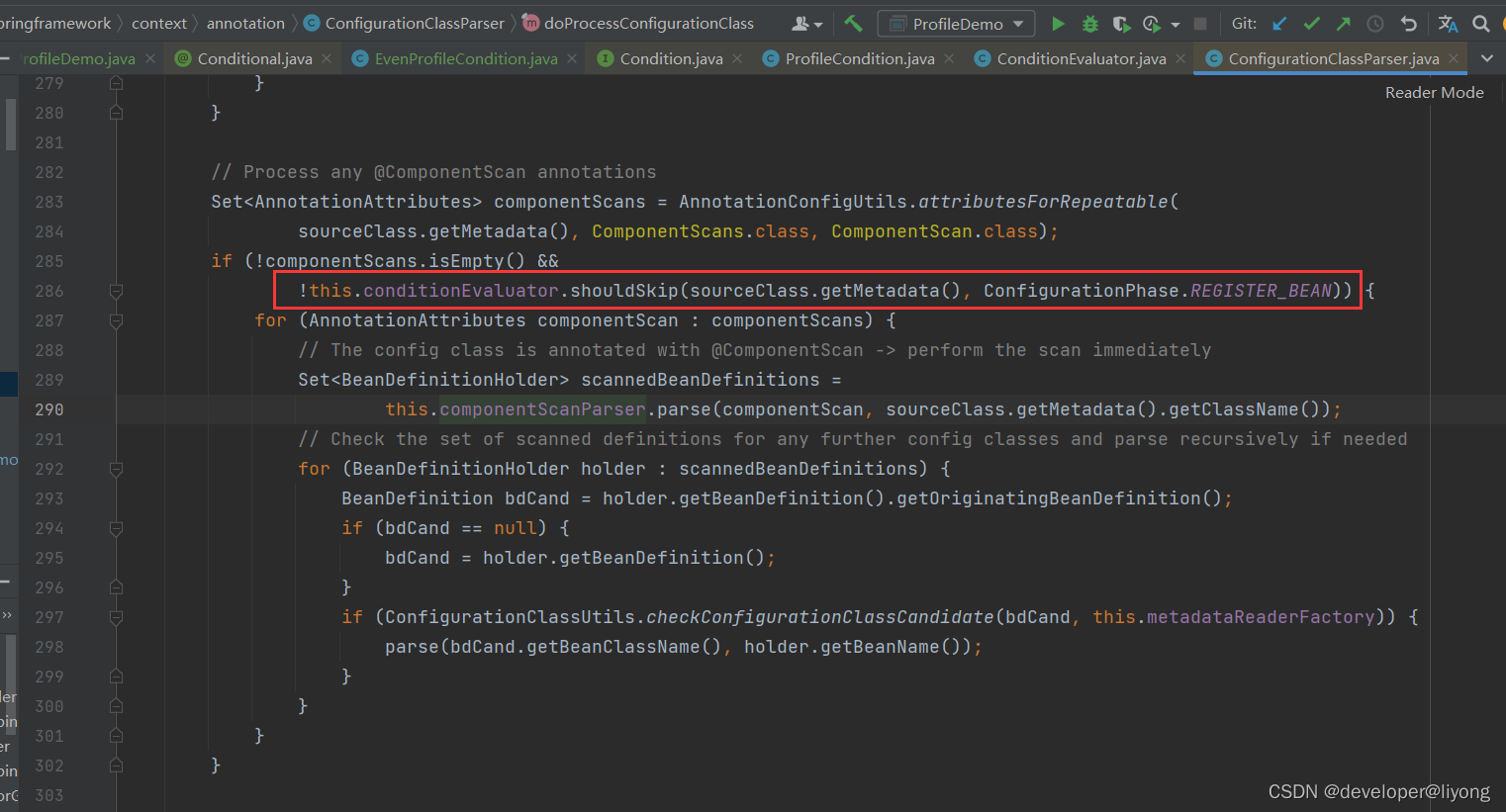
Spring-注解
Spring 注解分类 Spring 注解驱动模型 Spring 元注解 Documented Retention() Target() // 可以继承相关的属性 Inherited Repeatable()Spirng 模式注解 ComponentScan 原理 ClassPathScanningCandidateComponentProvider#findCandidateComponents public Set<BeanDefin…...

旧手机翻身成为办公利器——PalmDock的介绍也使用
旧手机有吧!!! 破电脑有吧!!! 那恭喜你,这篇文章可能对你有点用了。 介绍 这是一个旧手机废物利用变成工作利器的软件。可以在 Android 手机上快捷打开 windows 上的文件夹、文件、程序、命…...

期货交易的雷区
一、做自己看不懂的行情做交易计划一样要做有把握的,倘若你在盘中找机会交易,做自己看不懂的行情,即便你做进去了,建仓时也不会那么肯定,自然而然持仓也不自信,有点盈利就想平仓,亏损又想扛单。…...

东方通TongWeb结合Spring-Boot使用
一、概述 信创需要; 原状:原来的服务使用springboot框架,自带的web容器是tomcat,打成jar包启动; 需求:使用东方通tongweb来替换tomcat容器; 二、替换步骤 2.1 准备 获取到TongWeb7.0.E.6_P7嵌入版 这个文件,文件内容有相关对应的依赖包,可以根据需要来安装到本地…...
6.S081的Lab学习——Lab5: xv6 lazy page allocation
文章目录 前言一、Eliminate allocation from sbrk() (easy)解析: 二、Lazy allocation (moderate)解析: 三、Lazytests and Usertests (moderate)解析: 总结 前言 一个本硕双非的小菜鸡,备战24年秋招。打算尝试6.S081࿰…...
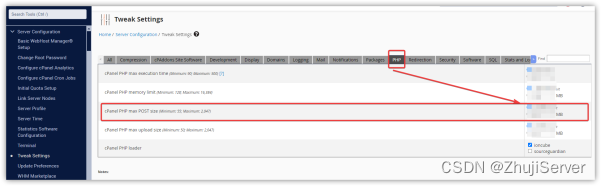
在WHM中如何调整max_post_size参数大小
今日我们在搭建新网站时需要调整一下PHP参数max_post_size 的大小,我们公司使用的Hostease的美国独立服务器产品默认5个IP地址,也购买了cPanel面板,因此联系Hostease的技术支持,寻求帮助了解到如何在WHM中调整PHP参数,…...

智能监控技术助力山林生态养鸡:打造智慧安全的养殖新模式
随着现代科技的不断发展,智能化、自动化的养殖方式逐渐受到广大养殖户的青睐。特别是在山林生态养鸡领域,智能化监控方案的引入不仅提高了养殖效率,更有助于保障鸡只的健康与安全。视频监控系统EasyCVR视频汇聚/安防监控视频管理平台在山林生…...

那些不起眼但很好玩的API合辑
那些不起眼但很好玩的API,为我们带来了许多出人意料的乐趣和惊喜。这些API可能看起来并不起眼,但它们却蕴含着无限的创意和趣味性。它们可以是一些小游戏API,让我们可以在闲暇时刻尽情娱乐;也可以是一些奇特的音乐API,…...

java —— 克隆对象、枚举
一、克隆对象 (一)在基本数据类型中,直接将对象 A 的值赋给对象 B,当更改对象 B 的时候,对象 A 的值保持不变。例如: public static void main(String[] args) {int a5;int ba; //将…...
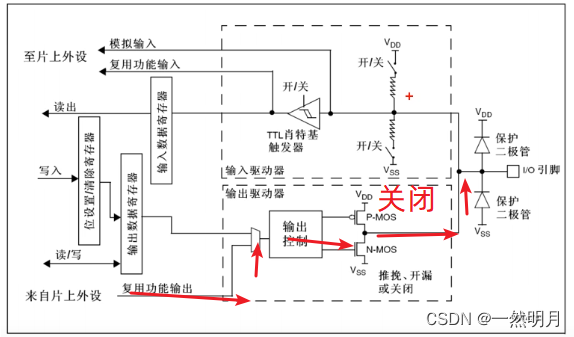
STM32-GPIO八种输入输出模式
图片取自 江协科技 STM32入门教程-2023版 细致讲解 中文字幕 p5 【STM32入门教程-2023版 细致讲解 中文字幕】 https://www.bilibili.com/video/BV1th411z7sn/?p5&share_sourcecopy_web&vd_source327265f5c70f26411a53a9226af0b35c 目录 编辑 一.STM32的四种输…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
