Scikit-Learn朴素贝叶斯
Scikit-Learn朴素贝叶斯
- 1、朴素贝叶斯
- 1.1、贝叶斯分类
- 1.2、贝叶斯定理
- 1.3、贝叶斯定理的推导
- 1.4、朴素贝叶斯及原理
- 1.5、朴素贝叶斯的优缺点
- 2、Scikit-Learn朴素贝叶斯
- 2.1、Sklearn中的贝叶斯分类器
- 2.2、Scikit-Learn朴素贝叶斯API
- 2.3、Scikit-Learn朴素贝叶斯实践(新闻分类与预测)
1、朴素贝叶斯
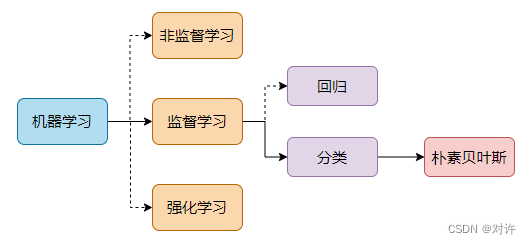
贝叶斯分类法是基于贝叶斯定理的统计学分类方法。它通过预测一组给定样本属于一个特定类的概率来进行分类。贝叶斯分类在机器学习知识结构中的位置如下:
1.1、贝叶斯分类
贝叶斯分类的历史可以追溯到18世纪,当时英国统计学家托马斯·贝叶斯发展了贝叶斯定理,这个定理为统计决策提供了理论基础。不过,贝叶斯分类得到广泛实际应用是在20世纪80年代,当时计算机技术的进步使得大规模数据处理成为可能
在众多机器学习分类算法中,贝叶斯分类和其他绝大多数分类算法都不同
例如,KNN、逻辑回归、决策树等模型都是判别方法,也就是直接学习出输出Y和特征X之间的关系,即决策函数 Y Y Y= f ( X ) f(X) f(X)或决策函数 Y Y Y= P ( Y ∣ X ) P(Y|X) P(Y∣X)
但是,贝叶斯是生成方法,它直接找出输出Y和特征X的联合分布 P ( X , Y ) P(X,Y) P(X,Y),进而通过 P ( Y ∣ X ) P(Y|X) P(Y∣X)= P ( X , Y ) P ( X ) \frac{P(X,Y)}{P(X)} P(X)P(X,Y)计算得出结果判定
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素贝叶斯(Naive Bayes)分类是贝叶斯分类中最简单,也是常见的一种分类方法
朴素贝叶斯算法的核心思想是通过特征考察标签概率来预测分类,即对于给定的待分类样本,求解在此样本出现的条件下各个类别出现的概率,哪个最大,就认为此待分类样本属于哪个类别
例如,基于属性和概率原则挑选西瓜,根据经验,敲击声清脆说明西瓜还不够成熟,敲击声沉闷说明西瓜成熟度好,更甜更好吃。所以,坏瓜的敲击声是清脆的概率更大,好瓜的敲击声是沉闷的概率更大。当然这并不绝对——我们千挑万选的沉闷瓜也可能并没熟,这就是噪声了。当然,在实际生活中,除了敲击声,我们还有其他可能特征来帮助判断,例如色泽、根蒂、品类等
朴素贝叶斯把类似敲击声这样的特征概率化,构成一个西瓜的品质向量以及对应的好瓜/坏瓜标签,训练出一个标准的基于统计概率的好坏瓜模型,这些模型都是各个特征概率构成的。这样,在面对未知品质的西瓜时,我们迅速获取了特征,分别输入好瓜模型和坏瓜模型,得到两个概率值。如果坏瓜模型输出的概率值更大一些,那这个瓜很有可能就是个坏瓜
1.2、贝叶斯定理
贝叶斯定理(Bayes Theorem)也称贝叶斯公式,其中很重要的概念是先验概率、后验概率和条件概率
1.2.1、先验概率
先验概率是指事件发生前的预判概率。可以是基于历史数据的统计,可以由背景常识得出,也可以是人的主观观点给出。一般都是单独事件概率
例如,如果我们对西瓜的色泽、根蒂和纹理等特征一无所知,按照常理来说,好瓜的敲声是沉闷的概率更大,假设是60%,那么这个概率就被称为先验概率
1.2.2、后验概率
后验概率是指事件发生后的条件概率。后验概率是基于先验概率求得的反向条件概率。概率形式与条件概率相同
例如,我们了解到判断西瓜是否好瓜的一个指标是纹理。一般来说,纹理清晰的西瓜是好瓜的概率更大,假设是75%,如果把纹理清晰当作一种结果,然后去推测好瓜的概率,那么这个概率就被称为后验概率
1.2.3、条件概率
条件概率是指一个事件发生后另一个事件发生的概率。一般的形式为P(B|A),表示事件A已经发生的条件下,事件B发生的概率
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
1.2.4、贝叶斯公式
贝叶斯公式是基于假设的先验概率与给定假设下观察到不同样本数据的概率提供了一种计算后验概率的方法。朴素贝叶斯模型依托于贝叶斯公式
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
贝叶斯公式中:
- P(A)是事件A的先验概率,一般都是人主观给定的。贝叶斯中的先验概率一般特指它
- P(B)是事件B的先验概率,与类别标记无关,也称标准化常量,通常使用全概率公式计算得到
- P(B|A)是条件概率,又称似然概率,一般通过历史数据统计得到
- P(A|B)是后验概率,后验概率是我们求解的目标
由于P(B)与类别标记无关,因此估计P(A|B)的问题最后就被我们转化为基于训练数据集样本先验概率P(A)和条件概率P(B|A)的估计问题
贝叶斯公式揭示了事件A在事件B发生条件下的概率与事件B在事件A发生条件下的概率的关系
更多关于条件概率、全概率公式与贝叶斯公式的介绍详见文章:传送门
1.3、贝叶斯定理的推导
根据条件概率公式可得
P ( A B ) = P ( B ∣ A ) P ( A ) P(AB)=P(B|A)P(A) P(AB)=P(B∣A)P(A)
同理可得
P ( B A ) = P ( A ∣ B ) P ( B ) P(BA)=P(A|B)P(B) P(BA)=P(A∣B)P(B)
设事件A与事件B互相独立,即 P ( A B ) P(AB) P(AB)= P ( B A ) P(BA) P(BA),则有
P ( B ∣ A ) P ( A ) = P ( A ∣ B ) P ( B ) P(B|A)P(A)=P(A|B)P(B) P(B∣A)P(A)=P(A∣B)P(B)
由此可得贝叶斯公式
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
1.4、朴素贝叶斯及原理
基于贝叶斯定理的贝叶斯模型是一类简单常用的分类算法。在假设待分类项的各个属性相互独立的前提下,构造出来的分类算法就称为朴素的,即朴素贝叶斯算法
所谓朴素,就是假定所有输入事件之间相互独立。进行这个假设是因为独立事件间的概率计算更简单,当然,也更符合我们的实际生产生活
朴素贝叶斯模型的基本思想是,对于给定的待分类项 X { x 1 , x 2 , . . . , x n } X\{{x_1,x_2,...,x_n}\} X{x1,x2,...,xn},求解在此项出现的条件下各个类别 P ( y i ∣ X ) P(y_i|X)
相关文章:

Scikit-Learn朴素贝叶斯
Scikit-Learn朴素贝叶斯 1、朴素贝叶斯1.1、贝叶斯分类1.2、贝叶斯定理1.3、贝叶斯定理的推导1.4、朴素贝叶斯及原理1.5、朴素贝叶斯的优缺点2、Scikit-Learn朴素贝叶斯2.1、Sklearn中的贝叶斯分类器2.2、Scikit-Learn朴素贝叶斯API2.3、Scikit-Learn朴素贝叶斯实践(新闻分类与…...

网页设计步骤总结
第一步:css重置 https://blog.csdn.net/BradenHan/article/details/132122504 第二步:媒体查询不同尺寸加载不同的css文件https://blog.csdn.net/Yi_Lesama/article/details/131184469 <!-- link元素中的CSS媒体查询 --> <link rel"styl…...

第十三期Big Demo Day亮点项目:CCarbon重塑碳交易生态,助力全球绿色发展
第十三期Big Demo Day活动即将于2024年5月28日在香港数码港的CyberArena隆重举行。我们荣幸地宣布,利用区块链技术优化全球碳交易CCarbon项目将亮相,参与精彩的项目路演。本次活动由ZeeprLabs、BiKing Exchange、Gather冠名赞助,Central Rese…...

python基础知识总结(第一节)
一、python简介: Python是一种解释型,面向对象的高级语言。 Pyhton的语法和动态类型,以及解释性语言的本质,使它一跃成为多数平台上写脚本和快速开发应用的编程语言。 python语言百度百科介绍 二、Python基础语法:…...

DOS学习-目录与文件应用操作经典案例-comp
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一.前言 二.使用 三.案例 案例 1: 基本比较 案例 2: 十进制显示差异 案例 3: 字符形式显…...

原神抽卡点名程序教程(直接下载用)
今天我要给大家分享一个在抖音上特别火的视频——原神抽卡点名程序教程。 废话不多说,直接上链接 :--点击下载原神抽卡程序 步骤1: 步骤2&am…...
gpt-4o继续迭代考场安排程序 一键生成考场清单
接上两篇gpt-4o考场安排-CSDN博客,考场分层次安排,最终exe版-CSDN博客 当然你也可以只看这一篇。 今天又添加了以下功能,程序见后。 1、自动分页,每个考场打印一页 2、添加了打印试场单页眉 3、添加了页脚 第X页,…...

php 设置时区
date_default_timezone_set() 设置所有日期/时间函数使用的默认时区 除了在脚本中使用此函数设置默认时区,还可以使用 INI 设置 date.timezone 设置默认时区。 参数 timezoneId 时区标识符,像 UTC、Africa/Lagos、Asia/Hong_Kong 或 Europe/Lisbon。…...
ArcGIS不同图斑设置不同的透明度
对于设置一个图层的整体的透明度,我们在 ArcGIS制作带蒙版的遥感影像地图http://mp.weixin.qq.com/s?__bizMzIzNjM2NTYxMg&mid2247509080&idx1&sn38dccf0a52bb3bb3758f57114ee38b72&chksme8da161bdfad9f0d363da90959a8524dcf2b60d0e8d999f8ebeef0…...

前端 CSS 经典:图片边框
前言:有这么一个业务,需要边框随着图片宽度的变化而变化,比如一些聊天的气泡框等。 实现原理:使用 border-image 属性 效果图: 实现代码: <!DOCTYPE html> <html lang"en"><he…...

异常有什么,异常类有什么
在Java中,异常(Exception)是一种在程序运行过程中出现的不正常情况。异常机制提供了一种从错误中恢复的途径。异常分为两大类:检查异常(Checked Exception)和运行时异常(Runtime Exception&…...
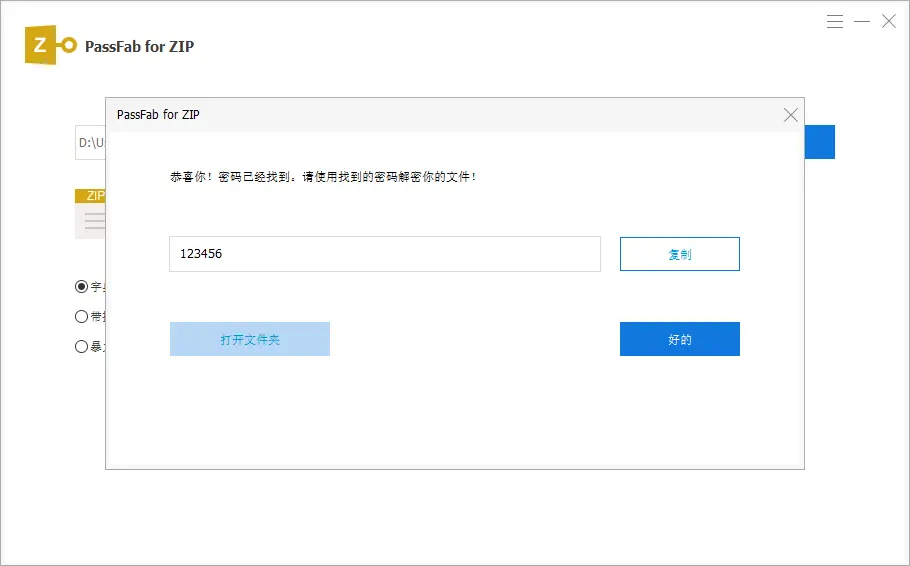
如何解压忘记了密码的加密zip压缩包?这两个方法收藏好!
加密是一种保护信息不被未经授权访问的重要手段。ZIP压缩包作为一种常见的文件压缩格式,zip文件加密是很多人都回去做的一件事情,那么zip加密文件如何解密?有几种方法可以解密呢?今天介绍几种方法给大家。 一、尝试常用密码 我们…...

java中,怎样用最简单方法实现写word文档
在跨平台环境中实现写word时,如果用现成的库,就会涉及跨平台兼容性问题,比如在安卓与java中实现写word的功能。还有一个问题就是,完全用程序生成word文档,工作量较大。所以采用了模板替换的方法。 docx文档本质就是一…...

大语言模型的工程技巧(三)——分布式计算
相关说明 这篇文章的大部分内容参考自我的新书《解构大语言模型:从线性回归到通用人工智能》,欢迎有兴趣的读者多多支持。 本文将讨论如何利用多台机器进行神经网络的分布式训练。利用多台机器来加速大语言模型的训练,是其获得成功的重要原…...
AI开发初体验:昇腾加持,OrangePi AIpro 开发板
文章目录 一、前言二、板子介绍2.1 拆箱2.2 板子规格2.2.1 常规项目2.2.2 扩展项目2.2.3 操作系统 2.3 点板画面 三、AI程序初体验3.1 新奇的地方3.2 运行第一个AI程序3.2.1 硬件连接3.2.2 串口连接3.2.3 开启外部IP端口3.2.4 查询板子IP地址3.2.5 了解 juypter lab 启动脚本&a…...

微服务架构下Docker容器技术与Kubernetes(K8S)
Kubernetes、微服务和Docker容器技术的结合提供了一个强大、灵活且高效的平台,能够应对现代应用程序的复杂性和动态性。Kubernetes的自动化管理、服务发现、负载均衡和配置管理,与Docker的标准化打包和运行环境相结合,最大化地发挥了微服务架…...

风萧萧兮易水寒,壮士一去兮不复还 的 rm 命令
风萧萧兮易水寒,壮士一去兮不复还 的 rm 命令 风萧萧兮易水寒,壮士一去兮不复还 的 rm语法几个示例/bin/rm Argument list too long – Linux”配合find与xargs完成删除海量文件使用find的delete选项 快速删除大文件 风萧萧兮易水寒,壮士一去…...

How Diffusion Models Work
introduction intuition goal 让神经网络学到图像是什么样的,一种方式是对数据添加不同级别的噪音,让神经网络能够区分细节/总体轮廓 训练一个神经网络去产生精灵 sampling nn 图像恢复 论文 https://zhuanlan.zhihu.com/p/686235079...
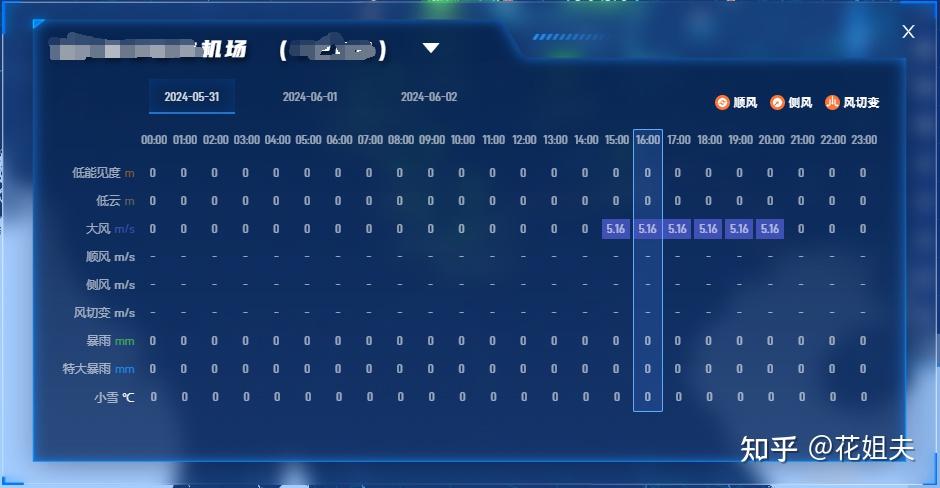
antd table列选中效果实现
前言 开发中有一个需要呈现不同时间点各个气象要素的值需求,我觉得一个table可以实现这类数据的展示,只是因为时间点时关注的重点,所以需要列选中效果,清晰的展示时间点下的要素数据。我选择的是antd的table组件,这个…...
Golang实现文件复制
方法:三种 package zdpgo_fileimport ("errors""io""os" )// CopyFile 使用io.Copy进行文件的复制,同时也会复制文件的所有权限 // param src 复制文件 // param des 目标文件 // return error 错误信息 func CopyFile(s…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...
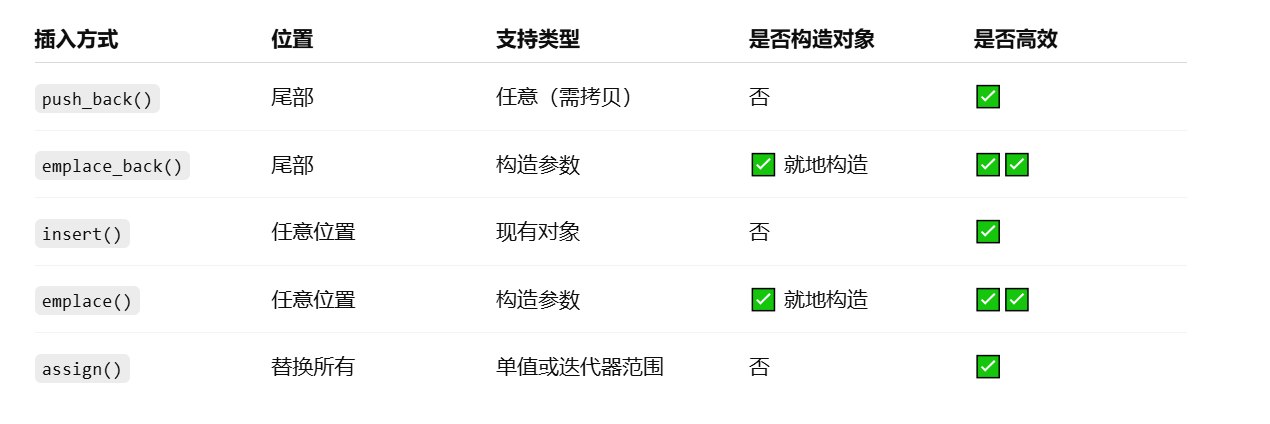
C++中vector类型的介绍和使用
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...
深入理解 C++ 左值右值、std::move 与函数重载中的参数传递
在 C 编程中,左值和右值的概念以及std::move的使用,常常让开发者感到困惑。特别是在函数重载场景下,如何合理利用这些特性来优化代码性能、确保语义正确,更是一个值得深入探讨的话题。 在开始之前,先提出几个问题&…...

RFID推动新能源汽车零部件生产系统管理应用案例
RFID推动新能源汽车零部件生产系统管理应用案例 一、项目背景 新能源汽车零部件场景 在新能源汽车零部件生产领域,电子冷却水泵等关键部件的装配溯源需求日益增长。传统 RFID 溯源方案采用 “网关 RFID 读写头” 模式,存在单点位单独头溯源、网关布线…...
