视觉SLAM十四讲:从理论到实践(Chapter7:视觉里程计1)
前言
学习笔记,仅供学习,不做商用,如有侵权,联系我删除即可
一、目标
1.理解图像特征点的意义,并掌握在单幅图像中提取特征点及多幅图像中匹配特征点的方法。
2.理解对极几何的原理,利用对极几何的约束,恢复图像之间的摄像机的三维运动。
3.理解PNP问题,以及利用已知三维结构与图像的对应关系求解摄像机的三维运动。
4.理解ICP问题,以及利用点云的匹配关系求解摄像机的三维运动。
5.理解如何通过三角化获得二维图像上对应点的三维结构。
二、特征点法
视觉里程(Visual Odometry):计算前后两帧位姿的变化量
VO主要有两个大类:特征点法和直接法。
特征点法最大的一个案例就是ORB-SLAM。
2.1 特征点
特征点由关键点(Key-point)和描述子(Descriptor)组成。
2.2 ORB特征
ORB(Oriented FAST and Rotated BRIEF)
关键点:FAST角点
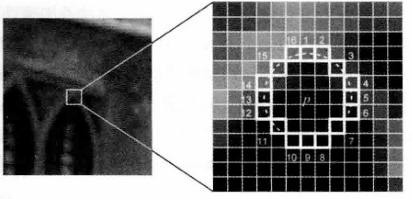



描述子:BRIEF(一种二进制描述子,速度非常快)
2.3 特征匹配
Hamming distance:两个二进制串之间的比较,相同为1,不同为0.
暴力匹配(Brute-Force Matcher):A中的每个特征点依次和B中所有的特征点比较距离,取最近的一个作为匹配点。
加速方法:快速最近邻(FLANN)
2.4 计算相机运动

三、2D-2D:对极几何
对极几何是研究两幅图像之间存在的关系的几何。它与场景结构无关,只依赖于相机的内外参数,可广泛用于图像匹配、三维重建方面。
3.1 对极约束

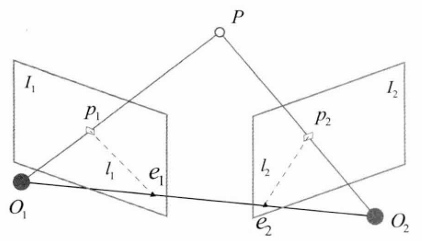
空间点P的世界坐标: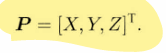
像素点p1,p2的像素坐标:![]() ,其中:K:内参矩阵,R,t:外参矩阵,s1p1和p1是投影关系,在齐次坐标上是相等的(尺度意义下相等)。
,其中:K:内参矩阵,R,t:外参矩阵,s1p1和p1是投影关系,在齐次坐标上是相等的(尺度意义下相等)。
把s除过取,再使用归一化坐标:![]()


基础矩阵F(和内参和外参都有关)和本质矩阵E (只和外参有关,内参已知的情况下)
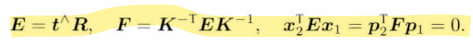
3.2 本质矩阵

最后可以得到如下方程:
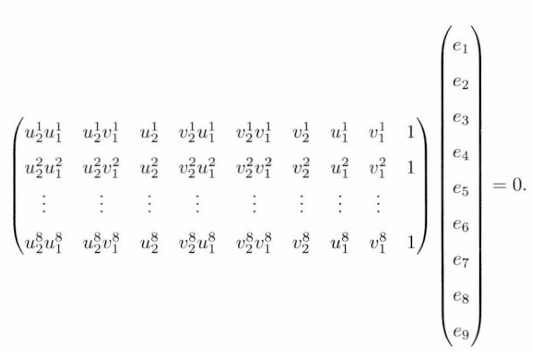
Ax=0可以用SVD方法计算出x的值。
从E中分离出R和t的方法是:![]() ,该方法会有4个可能的解
,该方法会有4个可能的解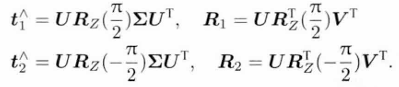
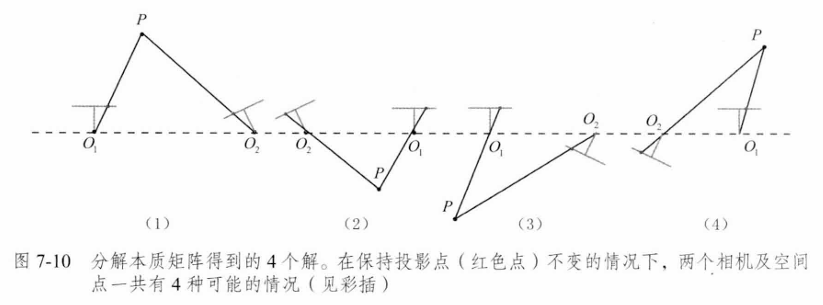
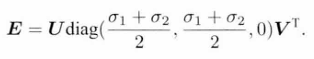
八点法用于初始换,但有尺度不确定性,而且不能用于纯旋转问题,多于八个点会用最小二乘法或RANSAC算法。
3.3 单应矩阵
平面方程: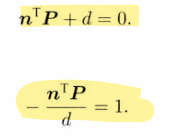 于是有:
于是有: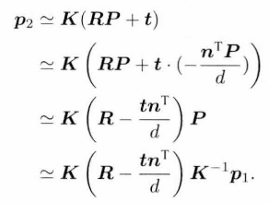 把中间部分记作H,则有:
把中间部分记作H,则有:![]() H即为单应矩阵。
H即为单应矩阵。
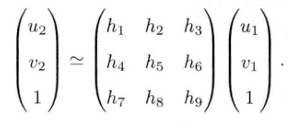
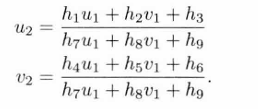 整理得:
整理得: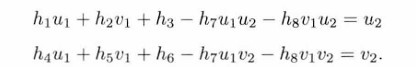
强制令h9=1,可得:

类似于Ax=b的方程,可用SVD分解或者最小二乘法优化算法求解。
四、三角测量
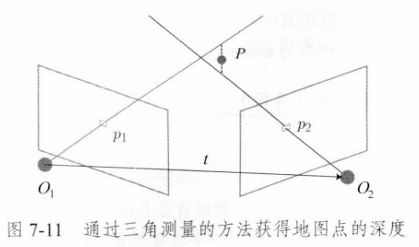
![]()
![]()
R,t已经求解出结果,只有深度未知,求解深度即可
但三角测量的误差与基线长度有关:
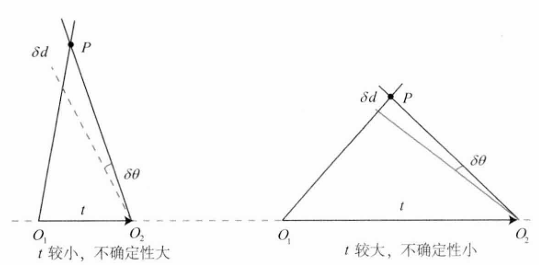
相机初始化:
特征点提取 --> 特征匹配 --> 求解E或F --> 根据E或F分解出R,t --> 三角化恢复三维坐标
五、3D-2D:PnP
真实点3D坐标和像素点的2D坐标已知,相机可以通过标定得到内参,进而计算相机位姿R,t的算法。
P3P,DLT,EPnP,UPnP等算法,PnP只是求解出一个初值,后面还需要用光束平差法(Bundle Adjustment, BA)进行优化。
5.1 DLT(直接线性变换)

一个点对可以提供两个方程,DLT有12个未知数,所以至少6个点对就可以求解。
现在最常用的是EPnP
总结
相关文章:

视觉SLAM十四讲:从理论到实践(Chapter7:视觉里程计1)
前言 学习笔记,仅供学习,不做商用,如有侵权,联系我删除即可 一、目标 1.理解图像特征点的意义,并掌握在单幅图像中提取特征点及多幅图像中匹配特征点的方法。 2.理解对极几何的原理,利用对极几何的约束&…...

c++指针的*
1.*运算符 *运算符被称为间接值(indirect value)或者解除引用(dereferencing)运算符 将其应用于指针可以得到该地址处存储的值 由于 * 也有乘法的意思,c通过上下文来确定是乘法还是解除引用 2.如何声明和初始化指针 …...

快团团大团长帮卖团长团长如何获得物流查询码?
一、功能说明 团长可自行生成物流查询码,直接将码发给顾客,顾客扫码可查询自己订单的物流状态! 用户扫码后,会出现用户在该团长处下单的所有快递订单。团员可查看该订单物流信息、进行退款申请,或直接联系团长。 二…...
基本SQL语句以及基本函数应用)
MySQL(二)基本SQL语句以及基本函数应用
1、基本SQL语句 MySQL中定义数据字段的类型对你数据库的优化是非常重要的。 MySQL支持多种类型,大致可以分为三类:数值、日期/时间和字符串(字符)类型。 - 函数应用在sql语句中 -- 临时表 select now() from dual;-- 数学函数 二进制 -- 返回x的绝对值 select a…...

fyne apptab布局
fyne apptab布局 AppTabs 容器允许用户在不同的内容面板之间切换。标签要么只是文本,要么是文本和一个图标。建议不要混合一些有图标的标签和一些没有图标的标签。 package mainimport ("fyne.io/fyne/v2/app""fyne.io/fyne/v2/container"//&…...

Python实现定时任务的方式
大家好,在当今数字化的时代,定时任务的需求在各种应用场景中频繁出现。无论是数据的定时更新、周期性的任务执行,还是特定时间点的操作触发,Python 都为我们提供了强大而灵活的手段来实现这些定时任务。当我们深入探索 Python 的世…...

微信小程序-网络数据请求(配置request合法域名)
1.小程序中网络数据请求的限制 出于安全方面的考虑,小程序官方对数据接口的请求做出了如下两个限制: (1)只能请求HTTPS类型的接口 (2)必须将接口的域名添加到信任列表中 如果要请求某个域名下的接口&am…...
栈和队列题目练习
本节小编选了两道题来加深对栈和队列的认识理解! 有效的括号 方法1:直接用栈的结构(动态数组) 本题可以用栈这个结构来解答,将(,{,[ 左括号压入栈中,然后取出栈顶元素与右括号),},]匹配。不匹配的话&…...

【排列问题】
问题: 已知某序列有n个元素,请编写程序打印出包含该序列所有元素的所有排列。 输入要求: 输入第1行为整数n,表示该序列元素的个数;第2行为n个整数,表示需要排列的序列元素。 输出要求:输出若…...

token 无感刷新
什么是 token 无感刷新?为什么需要 token 无感刷新?让我们想象一下有这么个场景:你登录一个系统成功后,玩了 10 分钟,发现登录失效了,又要你重新登录,然后又过 10 分钟,又失效了&…...

Netty SSL双向验证
Netty SSL双向验证 1. 环境说明2. 生成证书2.1. 创建根证书 密钥证书2.2. 生成请求证书密钥2.3. 生成csr请求证书2.4. ca证书对server.csr、client.csr签发生成x509证书2.5. 请求证书PKCS#8编码2.6. 输出文件 3. Java代码3.1. Server端3.2. Client端3.3. 证书存放 4. 运行效果4…...

4.nginx反向代理、负载均衡
nginx反向代理、负载均衡 一、反向代理1、语法2、注意事项3、后端服务器记录客户端真实IP3.1 在nginx反向代理时添加x-real-ip字段3.2 后端httpd修改combined日志格式3.3 后端是nginx的情况 二、负载均衡 upstream模块1、负载均衡作用2、调度算法3、配置应用 一、反向代理 隐藏…...
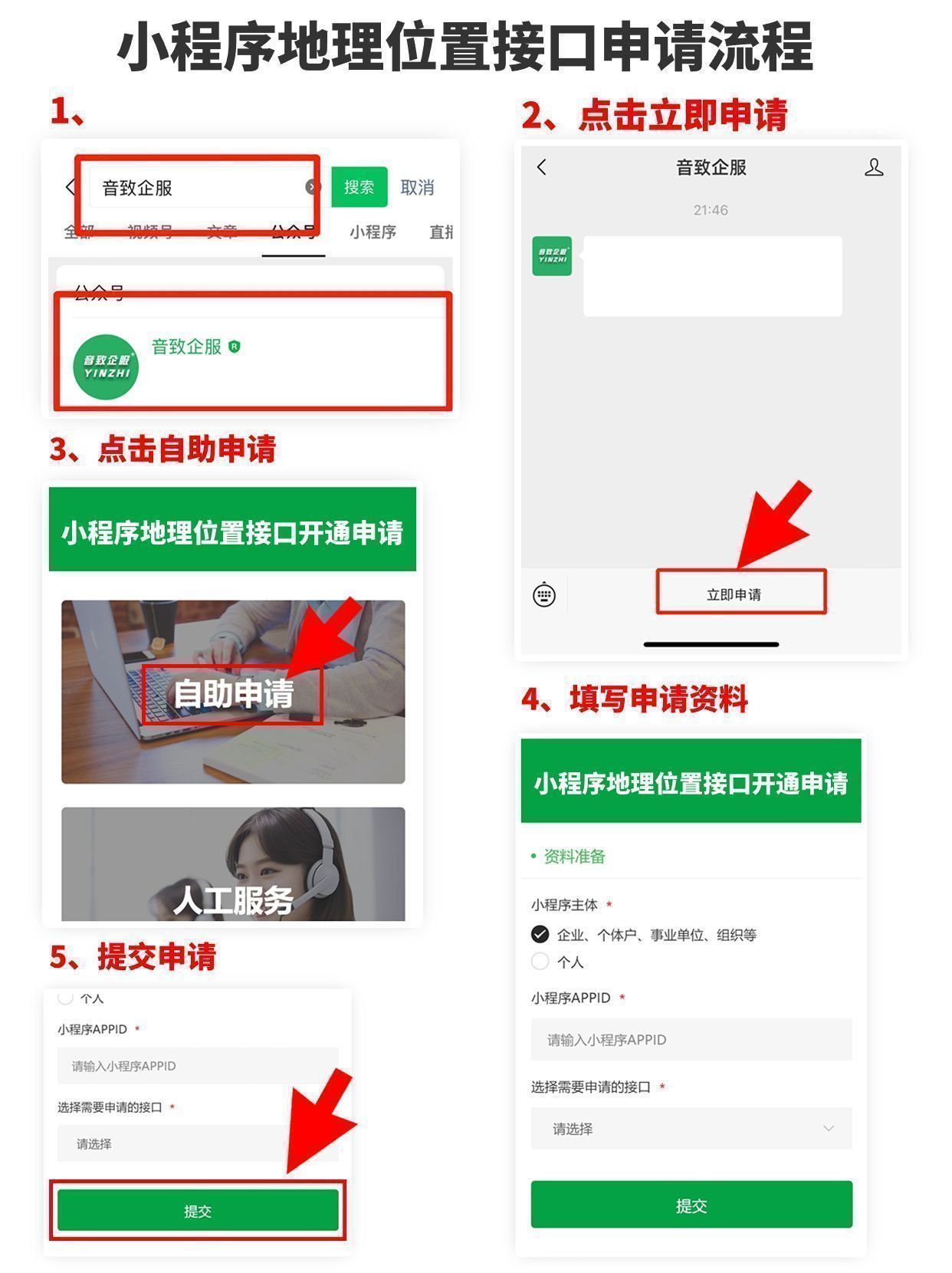
浅谈申请小程序地理位置权限的正确打开方式
小程序地理位置接口有什么功能? 这篇内容会教大家如何快速申请“获取当前的地理位置(onLocationChange)”接口,以便帮助大家顺利开通接口。以下内容是本人经历了多次的申请经历得出来的经验,来之不易,望大家…...

make modules 和 make modules_install
1. make modules 如:make ARCHarm64 CROSS_COMPILEaarch64-linux-gnu- modules 直接make,不加任何参数,就是make all,包含make modules。 make modules是单独编译模块,驱动被配置成M的都是modules,modul…...

docker 安装mysql,redis,rabbitmq
文章目录 docker 安装ngnix,mysql,redis,rabbitmq安装docker1.安装下载docker-ce源命令2.安装docker3.查看版本4.查看docker状态5.启动docker6.测试安装ngnix 安装mysql8.0.361.拉取mysql镜像2.安装mysql8 安装redis1.拉取redis7.0.11镜像2.安装redis3.进入容器内部…...
Windows配置java环境JDK
配置jdk环境非常简单,大概有以下几步: 下载jdk安装,然后双击进行安装配置环境变量(也不是一定非要配置环境变量,配置环境变量的好处就是,在任何位置,系统都可以找到安装路径,非常实用且方便) …...

英伟达驱动重装教程
离线安装NVIDIA驱动程序通常涉及下载驱动程序安装包并手动执行安装步骤。以下是详细步骤: 1. 下载NVIDIA驱动程序 首先,你需要在有网络连接的计算机上下载适合你系统的NVIDIA驱动程序安装包。可以从NVIDIA官方驱动下载页面下载。 选择你的GPU型号和操作系统,然后下载相应…...
【蓝桥杯嵌入式】 第六届国赛
目录 题目 配置 注意事项 代码 - 默写大师 EEPROM读写函数 LED驱动函数 ADC采集 上电初始化 LCD 按键 PWM互补输出 全部代码 hardware.c hardware.h control.c control.h main.c 题目 配置 注意事项 复制LCD的工程,先配置资源 --- 勾选完选项一…...

图片裁剪与上传处理方案 —— 基于阿里云 OSS 处理用户资料
目录 01: 通用组件:input 构建方案分析 02: 通用组件:input 构建方案 03: 构建用户资料基础样式 04: 用户基本资料修改方案 05: 处理不保存时的同步问题 06: 头像修改方案流程分析 07: 通用组件:Dialog 构建方案分析 08: 通用组件&…...
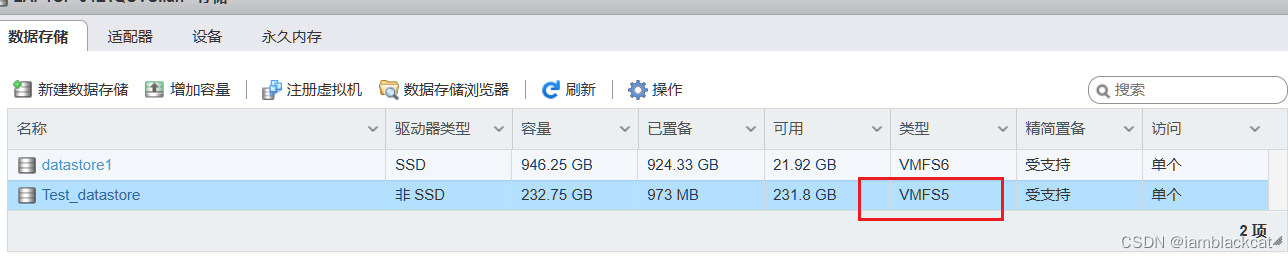
迷你主机Esxi 6.7挂载新硬盘
背景 硬件:零刻SER Pro 6 系统:vmware Exsi 6.7.0 Update 3 现有的硬盘槽位占满了,但空间不够用,想要通过USB外接移动硬盘来进行扩容。使用了一块250G的硬盘做测试。 步骤 TL;DR # 停止usbarbitrator服务 /etc/init.d/usbarbi…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
