堆结构知识点复习——玩转堆结构

        前言:堆算是一种相对简单的数据结构， 本篇文章将详细的讲解堆中的知识点， 包括那些我们第一次学习堆的时候容易忽略的内容， 本篇文章会作为重点详细提到。 

        本篇内容适合已经学完C语言数组和函数部分的友友们观看。

        

目录

什么是堆

建堆算法

向上调整算法

算法原理

如何计算parent

代码

向下调整算法

算法原理

寻找较小孩子 

代码

建堆

向下调整算法建堆

建堆过程

建堆的时间复杂度

向上调整算法建堆

建堆过程

建堆的时间复杂度

---

什么是堆

        首先来看什么是堆：

• 堆在逻辑结构上是一种完全二叉树。
• 堆的物理结构是数组。
• 堆分为大根堆和小根堆。
• 大根堆就是父亲节点大于左右孩子， 小根堆就是父亲节点小于左右父亲。

这里分析一个问题：堆相较于顺序表存不存在大量的空间浪费?

普通的二叉树如果使用数组来存储会出现大量的空间浪费。 但是堆是一颗完全二叉树， 完全二叉树就是除了叶子结点， 其他层上面的分支节点全都是满的。 而且叶子结点也全部是连续的， 这样的结构如果使用数组来存储就不会存在大量浪费的情况。 

逻辑结构的堆:

物理结构的堆:

建堆算法

建堆有两个算法:

• 向上调整算法
• 向下调整算法

向上调整算法

向上调整算法是从堆底向上调整。

向上调整算法的使用前提是：要向上调整的节点的前面的数组已经是一个堆。

算法原理

示例：

如图为一个小堆：

        1.现在插入一个0。那么这个0先插入在最后的位置。

         然后向上调整算法的过程就是：2.以刚刚插入的位置为child节点。 他的父亲为parent节点。 进行比较。

        3.比较child比parent小（注意， 现在是排的小堆， 小堆的父亲比左右孩子小）， 那么就要向上调整一下， 让父亲变成0， child变成3。（这里如果不小的话， 就说明此时就是一个小堆， 那么就结束调整。结束算法）

        4.然后让child变成指向parent的节点。 parent指向当前节点的父亲节点。 

       5. 然后回到2， 重新循环.  直到遇到child不小于parent或者child已经是堆顶元素。如图：

此时child指向堆顶。 没有父亲节点， 也就不需要再进行向上调整。 

时间复杂度：

• O(lgN)。

因为每次调整一下最坏的情况就是从堆底调整到堆顶。 对于一颗满二叉树（没写错， 就是满二叉树）来说， 有2 * h - 1 == N;   一棵满二叉树的高度是h == lg(N + 1)。所以它向上调整一次最坏的情况是调整lgN次（1被忽略）。那么对于完全二叉树来说， 比满二叉树还要少许多节点， 层数一样。 那么它的最坏调整次数也是lgN。所以时间复杂度就是lgN。 

如何计算parent

        假设有一个元素个数为6的小堆。
 

此时元素个数为6。 堆的物理结构就是:

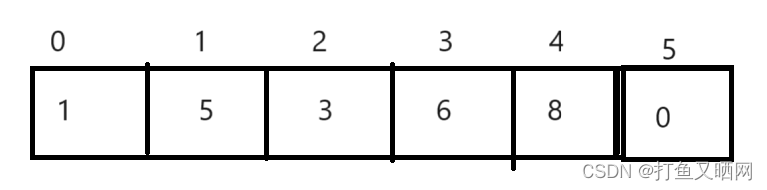
从逻辑结构中我们可以看到对于3这个位置来说， 它的左右两个孩子的下标是5和6。 而（5 - 1） / 2 == 2 ； （6 - 1） /   2 == 2；

对于图中的5节点来说，5的下标是1, 它的左右孩子的下标是3和4。 而 (3 - 1) / 2 == 1； （4 - 1）  / 2 == 1；

这里就有一个结论：

• parent == (child - 1) / 2;

代码

//向上调正算法
void AdjustUp(int* arr, int n)   //arr是一个等待调整的数组， n是这个数组的大小。
{//要使用向上调整算法， 说明此时arr的前n - 1个元素是一个堆。 第n个元素是等待向上调整的元素。int child = n - 1;              //第n个元素的下标是n - 1。     int parent = (child - 1) / 2;   //算出parent的位置while (child > 0)               //如果child到了堆顶， 那么就没有父亲， 也就不用比了。{if (arr[child] < arr[parent]) {swap(&arr[child], &arr[parent]);child = parent;parent = (parent - 1) / 2;}else                        //如果孩子节点比父亲节点还大， 那么也不用比了， 此时就是个堆{break;}}
}

向下调整算法

算法原理

向下调整算法要求左右两棵子树都是堆， 然后以根节点为基准向下进行调整。 

示例:

        如图是一个数组

这个数组如果转化为堆的逻辑结构就是如图:

        观察逻辑结构， 我们很容易可以观察到9的左右两边都是小堆。符合向下调整算法的要求(如果左右两边有一边不是堆结构， 那么就不可以使用向下调整算法)，向下调整算法的流程为:

        1.  定义parent指向9的位置。 child指向左右边小的那个节点。 因为这里1比5小， 所以指向1。

          2.  然后比较child和parent。 如果child小于parent。 那么就要交换位置， 否则退出循环， 算法结束。

        3.  交换数据之后移动指针， parent指向child指向的节点。 child指向当前节点的左右孩子中较小的那个。

        4.  然后重复2的操作。 一直到child大于parent或者查出数组的范围。退出循环， 算法结束.

时间复杂度

• O(lgN)

       时间复杂度的计算和向上调整算法一样。 对于一个堆来说，最坏的情况就是从堆顶向下调整到堆底，那么调整次数就是树的高度次。 而树的高度的数量级是lgN级别。 所以时间复杂度就是O（lgN)。

寻找较小孩子 

        可以利用假设法寻找左右孩子中较小的那一个。       

        对于一个父亲节点， 它的左孩子的下标是child == parent * 2 + 1; 右孩子就是child == parent * 2 + 2;

假设过程如下:

•      先假设左孩子是较小的那个孩子。
•      然后， 就比较左孩子和右孩子
•      如果右孩子比左孩子更小， 那么就让右孩子变成较小的那个孩子。

代码

//向下调整算法
void AdjustDown(int* arr, int n, int parent)  //arr是要调整的数组， n是要建堆数组的大小。 parent下调的基准点。
{int child = parent * 2 + 1;               //先假设孩子节点是父亲节点的左边while (child < n)                         {//如果右孩子更小， 那么就让child变成父亲节点的右边if (child + 1 < n && arr[child + 1] < arr[child]) child++;              if (arr[child] < arr[parent]) {swap(&arr[child], &arr[parent]);parent = child;child = child * 2 + 1;}else {break;}}
}

建堆

向下调整算法建堆

建堆过程

        向下调整建堆需要保证那个要调整的节点的左右子树都是堆。 所以我们进行向下调整建堆的时候要从堆底向堆顶建堆。 具体过程如下:

假设如图为要调整成为堆的数组的逻辑结构:

       我们首先要从堆底的第一个非叶子节点开始向下调整，就像下图的最右边的那个红框框。 从这个红框框中的非叶子节点开始向下调整。 从右向左， 先将这一层的非也节点全部调整为堆。 

       此时， 这一层往下都是堆结构， 那么我们就可以向上一层进行调堆。

 

 当我们调好红框框中的堆后， 就可以调绿框框的堆。 

 然后绿框框的堆调好之后我们就可以调以堆顶为基准的堆， 那么这整个数组就建堆完成。 

 

建堆的时间复杂度

        个人认为堆里面最难的一部分内容， 就是建堆的时间复杂度。 可能有的友友会说， 建堆的时间复杂度是O（N * lgN) 。 博主一开始也以为是O（N * lg N）， 但是其实只有向上调整建堆是O（N * lgN）。 而向下调整建堆的时间复杂度其实是O（N）。 为什么？ 这里其实用到了高中的错位相减法求时间复杂度。

        假设这是一个h层的树结构。

那么当我们建堆的时候。  从倒数第二层开始向下调整。假设一共h层。证明如下：

• 第h - 1层有2 ^ (h - 2) 个节点， 每一个节点最多向下调整一次。 一共调整2 ^ (h - 2) * 1次。
• 倒h - 2层有2 ^ (h - 3) 个节点， 每一个节点最多向下调整两次。 一共调整2 ^ (h - 3) * 2次。
• 倒h - 3层有2 ^ (h - 4) 个节点， 每一个节点最多向下调整三次。 一共调整2 ^ (h - 4) * 3次。
• …………
• …………
• …………
• 第三层有2 ^ 2个节点， 每一个节点最多向下调整h - 3次。一共调整 2 ^ 2 * (h - 3)次。
• 第二层有2 ^ 1个节点， 每一个节点最多向下调整h - 2次。 一共调整2 ^ 1 * (h - 2)次。
• 第一层有2 ^ 0个节点， 每一个节点最多向下调整h - 1次。 一共调整2 ^ 0 * (h - 1)次。

这些次数加起来就是一个等差乘以等比类型的数列求和。

        T(h) == 2 ^ 0 * (h - 1) + 2 ^ 1 * (h - 2) + 2 ^ 2 * (h - 3) + …… + 2 ^ (h - 4) * 3 + 2 ^ (h - 3) * 2 + 2 ^ (h - 2) * 1

   2 * T(h) ==             2 ^ 1 * (h - 1) + 2 ^ 2 * (h - 2) + …… + 2 ^ (h - 4) * 4 + 2 ^ (h - 3) * 3 + 2 ^ (h - 2) * 2 + 2 ^ (h - 1) * 1;

        所以 ：T(h) == - (h - 1) + 2 + 2 ^ 2 + 2 ^ 3 + …… + 2 ^ (h - 2) + 2 ^ (h - 1)

                           == 2 ^ h - h;

由完全二叉树的规则: N == 2 ^ h - 1； 将这个式子带入上面T(h)就能得到T(N) == N + 1 - lgN。

由大O的渐进表示法可知， 时间复杂度为O（N）。

代码：

void CreatHeap(int* arr, int sz) 
{for (int i = (sz - 1 - 1) / 2; i >= 0; i--)   //(sz - 1) / 2是第一个非叶节点。{//向下调整建堆AdjustDown(arr, sz, i);    //以i为基准， 最大下标为sz;}
}

向上调整算法建堆

建堆过程

向上调整建堆需要前面的数组为堆结构。 所以和向下调整建堆相反，它是从堆顶开始建堆。建堆过程需要从下标为0开始向后遍历进行向上调整建堆。 建堆过程如下：

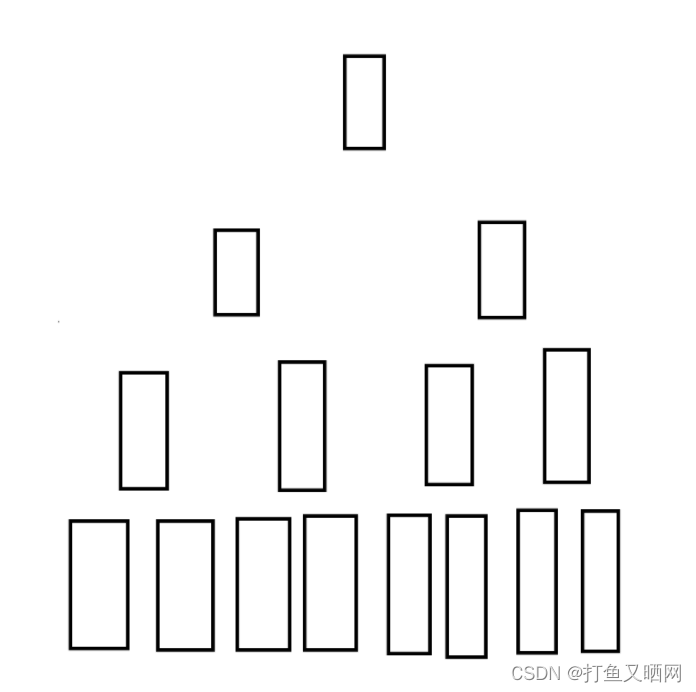
如图为一树结构。 

对于这个结构。 我们要先从第一个堆顶位置开始向下调。

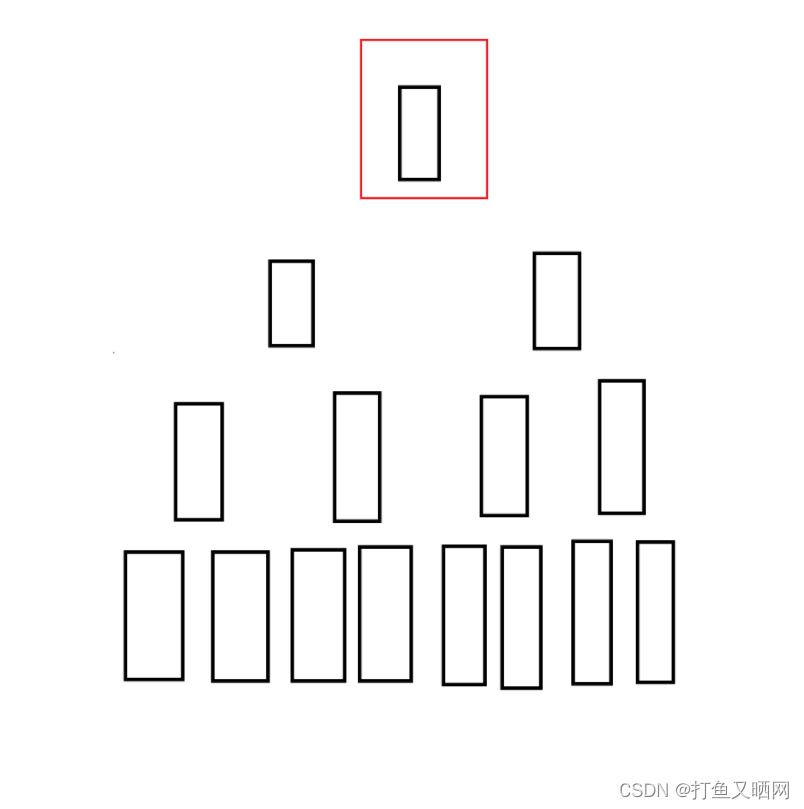
然后调第二个元素

再调第三个元素， 第四个元素……第n个元素。 依次类推。

建堆的时间复杂度

        我们同样使用前面的方法， 将每一层的节点的调整次数列出来。 如下:

• 第一层：2 ^ 0节点， 调整0次
• 第二层：2 ^ 1节点， 每个节点调整1次。一共调整2 ^ 1 * 1次。
• 第三层：2 ^ 2节点， 每个节点调整2次。一共调整2 ^ 2 * 2次。
• 第四层：2 ^ 3节点， 每个节点调整3次。 一共调整2 ^ 3 * 3次。
• …………
• …………
• …………
• 第h - 2层: 2 ^ (h - 3)节点， 每个节点调整h - 3次。 一共调整2 ^ (h - 3) * (h - 3)次。
• 第h - 1层：2 ^ (h - 2)节点， 每个节点调整h -2次。 一共调整2 ^ (h - 2) * (h - 2)次。
• 第h 层： 2 ^ (h - 1)节点， 每个节点调整h - 1次。 一共调整2 ^ (h - 1) * (h - 1)次。

       利用N == 2 ^h - 1代入可得最后一层节点个数大约为N / 2。（这其实也是满二叉树的性质。）

       所以我们只需要看第h层调整需要的节点个数, 因为对于一棵完全二叉树来说， 最后一层的节点个数相当于其所有节点个数的一半。 那么每个节点向上调整的次数都是lgN。 所以对于向上调整算法建堆的时间复杂度就是O(N * lgN)。

代码:

void CreatHeap(int* arr, int sz) 
{for (int i = 0; i < sz; i++)  {//向上调整建堆AdjustUp(arr, i);    //以i为调堆最后一个元素}
}