解锁私域流量的奥秘:构建独特的私域生态
大家好,我是来自一家深耕私域电商领域的技术创新公司,担任资深产品经理一职,已积累了多年的行业经验和独到见解。今天,我想和大家共同探讨私域流量的核心内涵,以及它为何在当前的商业环境中变得如此重要。在私域运营中,深化用户关系并提升关系价值,是实现用户长期留存和转化的关键所在。

深入解读私域流量
私域流量,从本质上来说,是一个企业可以独立控制、自由沟通、且能重复利用的用户资源池。它超越了简单的用户数据和信息,更包含了与用户的深度互动和关系维护。私域流量的核心价值在于其独享性和可控性,这为企业提供了直接触达用户、了解用户需求、并精准满足这些需求的途径。

私域流量的战略价值
在当今互联网环境中,公域流量的获取成本不断攀升,而私域流量则成为了企业持续发展的重要基石。私域流量不仅能够帮助企业降低营销成本,还能通过深度运营提升用户的忠诚度和复购率。此外,私域流量还能够为企业提供丰富的用户数据支持,帮助企业更好地理解市场趋势和用户需求,从而优化产品和服务。
私域电商的演进之路
从社交媒体平台的兴起,到微信生态的繁荣,再到如今私域电商的蓬勃发展,我们可以看到私域流量在国内市场的巨大潜力和广阔前景。越来越多的品牌和企业开始重视并布局私域电商,通过搭建自己的私域生态来提升品牌影响力并实现商业价值。

面对挑战与机遇
在私域流量的运营过程中,企业也面临着诸多挑战。例如,社交平台的规则限制、用户数据的安全和隐私保护等问题都需要企业予以关注和解决。然而,这些挑战也为企业带来了机遇。通过不断创新和优化私域生态的搭建方式,企业可以突破限制,实现更高效的用户运营和转化。
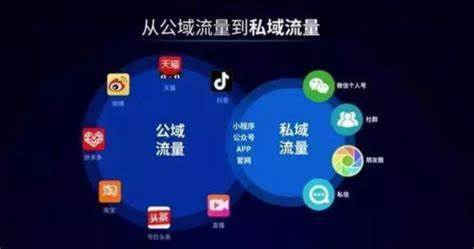
构建独特的私域生态
为了打造属于自己的私域生态,许多企业开始选择开发自己的App。通过App,企业可以为用户提供更加个性化和便捷的服务体验,同时也能够收集到更加丰富的用户数据。虽然从公域流量中引流到私域生态需要一定的成本和时间投入,但长远来看,这将为企业带来更加稳定、可持续的流量来源和更高的商业价值。
如果您对私域电商的发展趋势感兴趣,或者想了解更多关于私域流量运营的知识和技巧,欢迎与我们联系。我们将为您提供专业的咨询和服务,共同探索私域电商的无限可能!
相关文章:

解锁私域流量的奥秘:构建独特的私域生态
大家好,我是来自一家深耕私域电商领域的技术创新公司,担任资深产品经理一职,已积累了多年的行业经验和独到见解。今天,我想和大家共同探讨私域流量的核心内涵,以及它为何在当前的商业环境中变得如此重要。在私域运营中…...

在CentOS系统上安装Oracle JDK(华为镜像)
在CentOS系统上安装Oracle JDK(华为镜像) 先爱上自己,再遇见爱情,不庸人自扰,不沉溺过去,不为自己的敏感而患得患失,不为别人的过失而任性,这才是终身浪漫的开始。 https://repo.huaweicloud.com/java/jdk …...
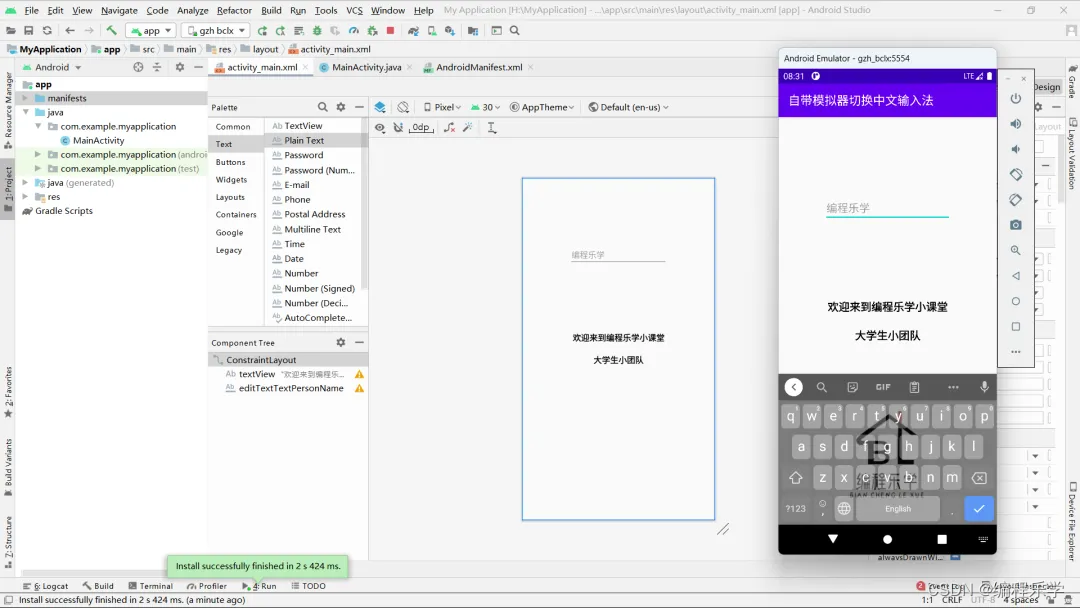
7 步解决Android Studio模拟器切换中文输入
详细步骤传送地址:Android Studio 模拟器切换中文输入 目录 01 问题概述 02 模拟器的调试 01 问题概述 大家在使用Android Studio 软件进行项目演示时总会遇到一些输入框需要输入中文汉字的情况,由于AS自带的模拟器基本都是英文,这时就有同…...

如何搭建B2B2C商城系统?开发语言、功能扩展、优势分析
如今,越来越多的企业意识到单靠第三方电商平台不足以快速实现品牌曝光和销售增加,相反还有诸多限制。 因此,搭建一个B2B2C商城也就成为企业发展业务的首选,既可以满足自营和商家入驻的需求,功能操作又灵活,…...

Rust的高效易用日志库—tklog
很多人习惯于python,go等语言基础工具库的简单易用;在使用rust时,可能感觉比较麻烦,类似日志库这样的基础性工具库。tklog提供用法上,非常类似python等Logger的日志库用法,用法简洁;基于rust的高…...
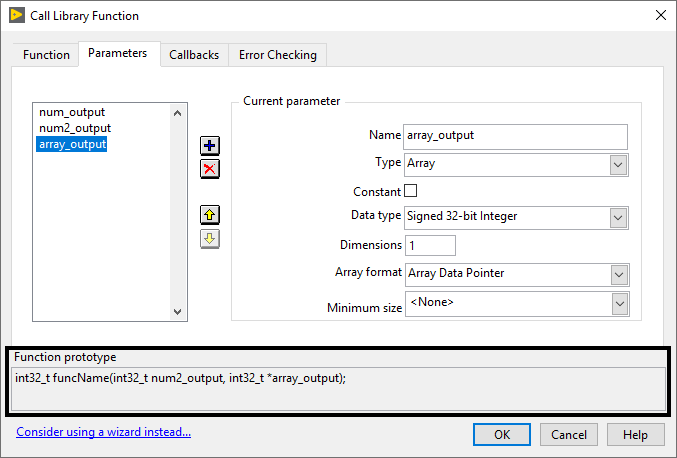
LabVIEW调用外部DLL(动态链接库)
LabVIEW调用外部DLL(动态链接库) LabVIEW调用外部DLL(动态链接库)可以扩展其功能,使用外部库实现复杂计算、硬件控制等任务。通过调用节点(Call Library Function Node)配置DLL路径、函数名称和…...
Tkinter笔记(十六):Radiobutton选项功能按钮(单选按钮))
Python图形界面(GUI)Tkinter笔记(十六):Radiobutton选项功能按钮(单选按钮)
在tkinter库中,选项功能按钮Radiobutton是一个常用的控件,用于从多个选项中选择一个,从而实现相关的交互功能。 其余笔记:【Python图形界面(GUI)Tkinter笔记(总目录)】 【一】书写:tkinter.Radiobutton(父窗口对象,参数1,参数2,...) 【二】Radiobutton控件常用参数…...
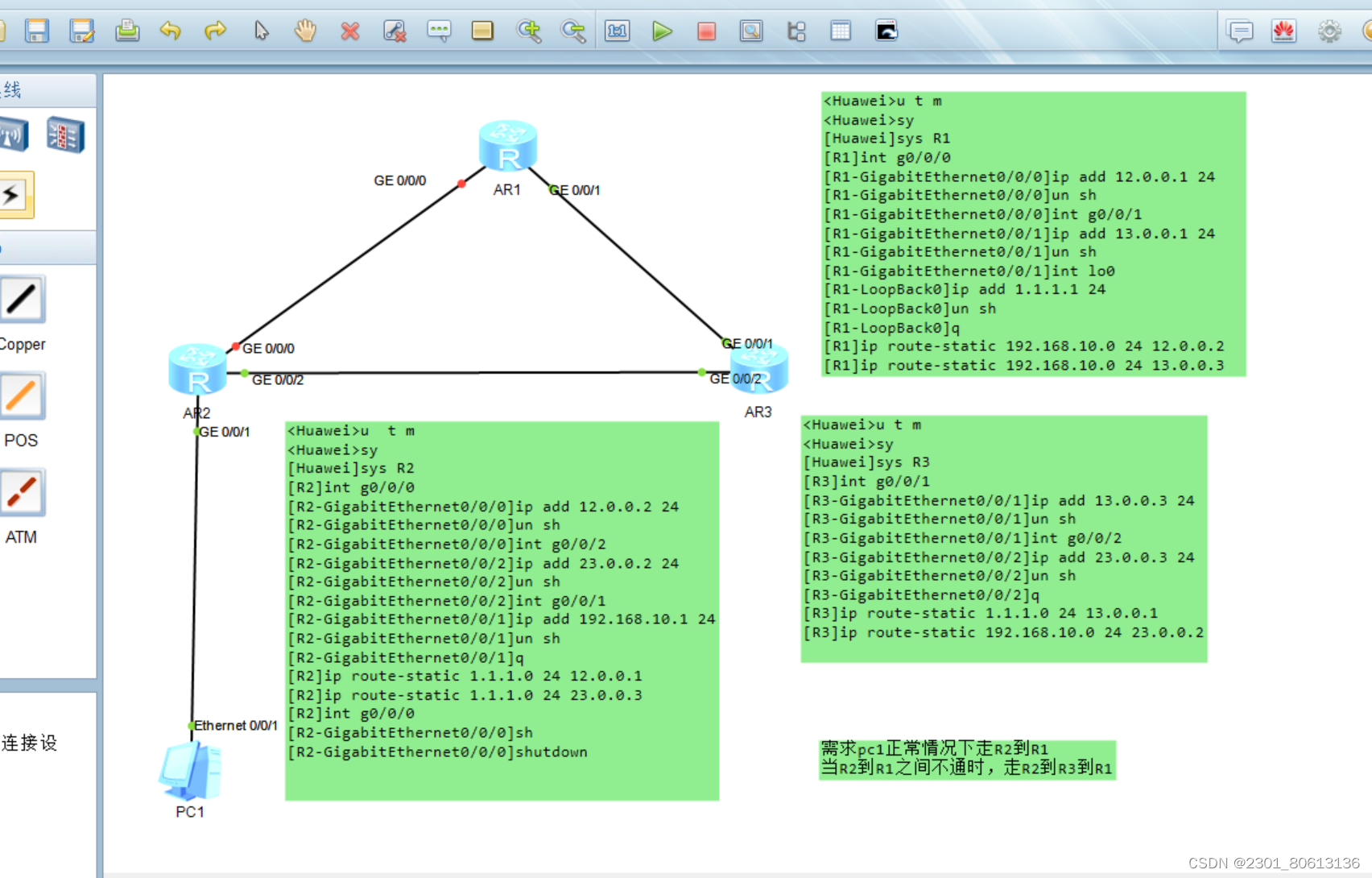
静态路由原理与配置
文章目录 路由器的工作原理路由根据路由表转发数据 路由表的形成路由表路由表的形成 静态路由和默认路由静态路由默认路由 路由器转发数据包的封装过程源目地址变化 交换与路由对比路由工作在网络层交换工作在数据链路层 静态路由和默认路由的配置 路由器的工作原理 路由 路由…...

Android 开机动画的启动过程BootAnimation(基于Android10.0.0-r41)
文章目录 Android 开机动画的启动过程BootAnimation(基于Android10.0.0-r41)1.开机动画的启动过程概述2.为什么设置了属性之后就会播放? Android 开机动画的启动过程BootAnimation(基于Android10.0.0-r41) 1.开机动画的启动过程概述 下面就是BootAnimation的重要部…...
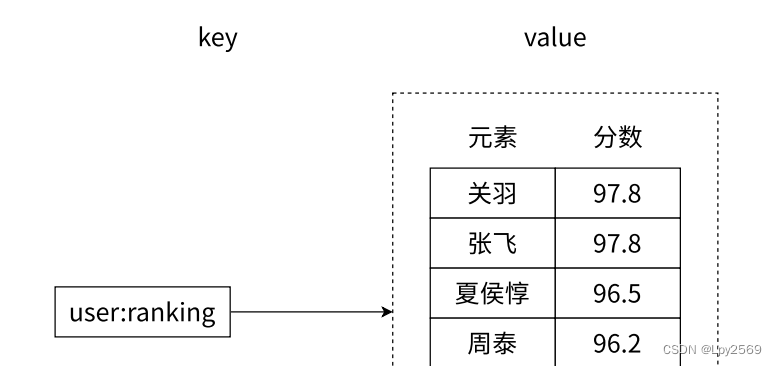
Redis 中的 Zset 数据结构详解
目录 用法 1. 增 2. 删 3. 查 4. 交,并 编码方式 应用场景 Redis 中的 Zset(有序集合)是一种将元素按照分数进行排序的数据结构。与上篇写的SetRedis 中的 Set 数据结构详解不同,Zset 中的每个元素都关联一个浮点数类型的…...

Python网页处理与爬虫实战:使用Requests库进行网页数据抓取
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...
HOW - vscode 使用指南
目录 一、基本介绍1. 安装 VS Code2. 界面介绍3. 扩展和插件4. 设置和自定义 二、常用界面功能和快捷操作(重点)常用界面功能快捷操作 三、资源和支持 Visual Studio Code(VS Code)是一款由微软开发的免费、开源的代码编辑器&…...

刚刚!《国家科学技术奖励条例》迎来最新修订
【SciencePub学术】《国务院关于修改〈国家科学技术奖励条例〉的决定》已经于2024年5月11日国务院第32次常务会议通过,现予公布: 国务院决定对《国家科学技术奖励条例》作如下修改: 一、将第二条修改为:“国家设立下列国家科学技术…...
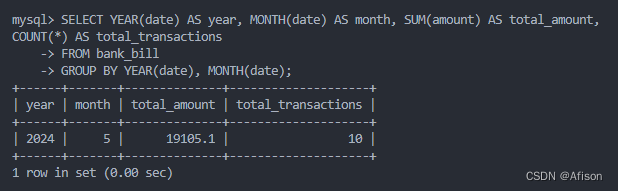
MySQL -- SQL笔试题相关
1.银行代缴花费bank_bill 字段名描述serno流水号date交易日期accno账号name姓名amount金额brno缴费网点 serno: 一个 BIGINT UNSIGNED 类型的列,作为主键,且不为空。该列是自动增量的,每次插入新行时,都会自动递增生成一个唯一的…...

VB6 MQTT为什么在物联网应用中使用 MQTT 而不是 HTTP?
有需要VBA,VB6,VB.NET等方面的MQTT的可以找我 一、MQTT简介 MQTT被广泛用于物联网(IoT:Internet of Things)领域,其中大量的设备需要进行实时通信和数据交换。它采用了一种发布/订阅(publish/subscribe)模型,其中消息的发送者(发布者&#…...

软设之希尔排序
假设有n个元素,先取一个小于n的整数d1作为一个增量,把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组中进行直接插入排序;然后,取第二个增量d2<d1重复上诉的分组和排序,直到所取得增量dt1&#…...
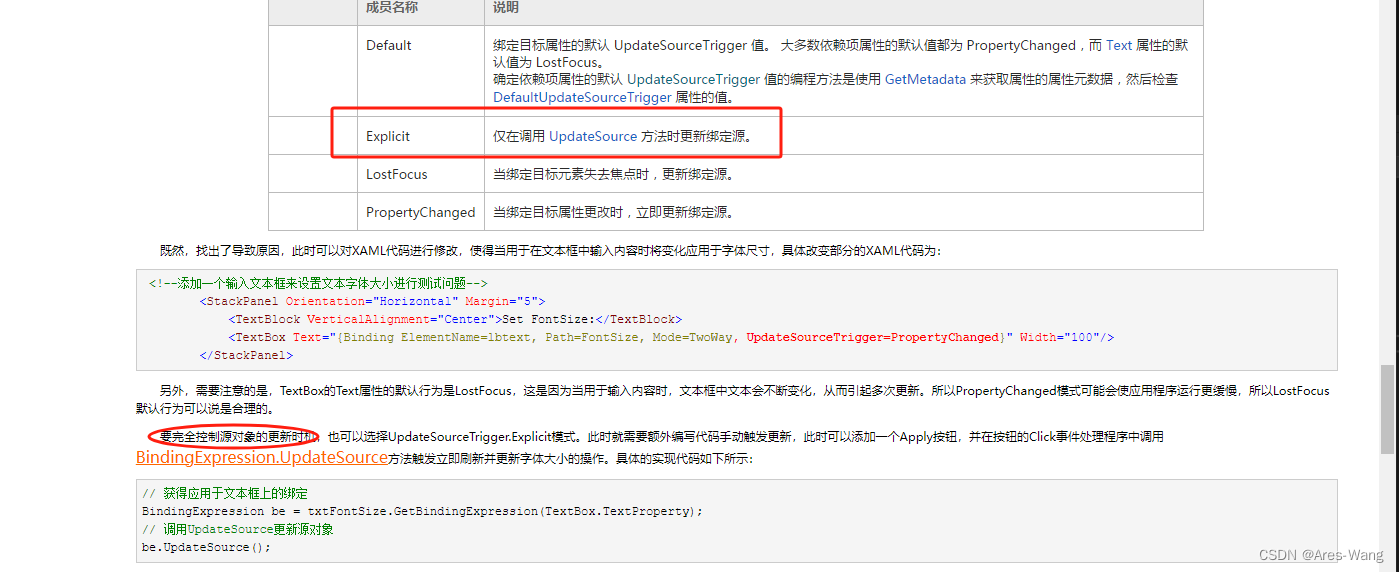
WPF Binding对象
在WinForm中,我们要想对控件赋值,需要在后台代码中拿到控件对象进行操作,这种赋值形式,从根本上是无法实现界面与逻辑分离的。 在WPF中,微软引入了Binding对象,通过Binding,我们可以直接将控件与…...

Educational Codeforces Round 127 D. Insert a Progression
Insert a Progression time limit per test: 2 second memory limit per test: 256 megabytes input: standard input output: standard output You are given a sequence of n n n integers a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an. You are also giv…...

树莓集团:构筑全国数字影像生态链
在数字化浪潮席卷全球的今天,数字影像技术正以前所未有的速度改变着我们的生活。成都树莓集团以远见卓识和坚定步伐,专注于全国数字影像生态链的建设,不断推动着文创产业的创新与发展。 树莓集团致力于打造一个完整的数字影像生态链ÿ…...
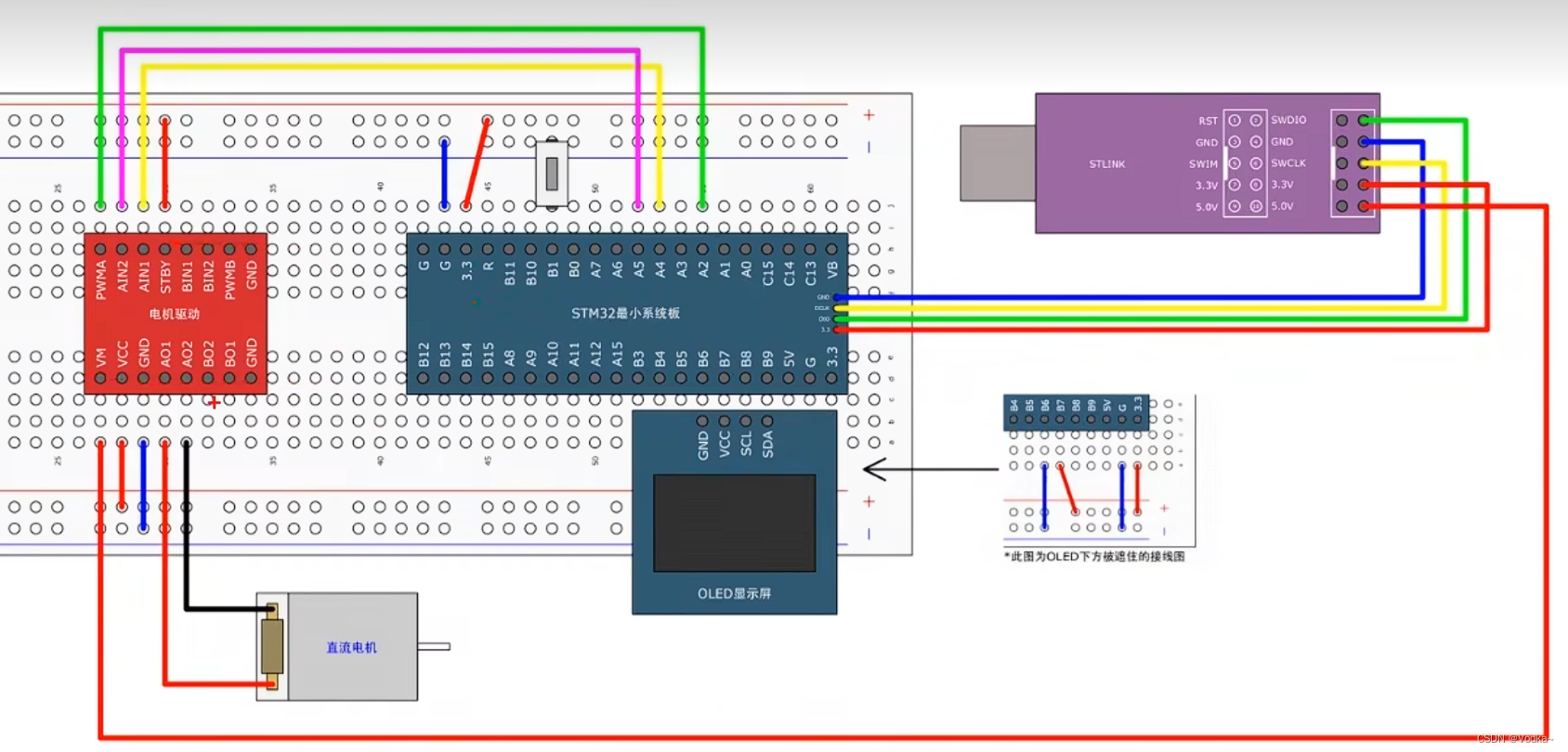
物联网——TIM定时器、PWM驱动呼吸灯、舵机和直流电机
定时器概念(常用于输出PWM波形,驱动电机) 时间脉冲数时钟周期; 这里的脉冲数6553665536,支持定时器级联,从而延长定时 定时器类型 基本定时器原理图(UI:更新中断, U:更新事件&#…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
