代码随想录算法训练营第38天 | 509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
代码随想录算法训练营第38天 | 509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
- 理论基础
- 自己看到题目的第一想法
- 看完代码随想录之后的想法
链接: 509. 斐波那契数
链接: 70. 爬楼梯
链接: 746. 使用最小花费爬楼梯
理论基础
五部曲:
1.确定dp数组(dp table)以及下标的含义
2.确定递推公式
3.dp数组如何初始化
4.确定遍历顺序
5.举例推导dp数组
自己看到题目的第一想法
509.斐波那契数:直接看题解。
70.爬楼梯:
746.使用最小花费爬楼梯:
看完代码随想录之后的想法
509.斐波那契数:
五部曲上秤!
(1)确定dp数组以及下标的含义:dp[i]的定义为:第i个数的斐波那契数值是dp[i]
(2)确定递推公式:直接有递推公式:状态转移方程dp[i]=dp[i-1]+dp[i-2]
(3)dp数组如何初始化:dp数组的初始化题目给了,dp[0]=0,dp[1]=1
(4)确定遍历顺序:从递归公式可以看出,dp[i]依赖dp[i-1]和dp[i-2],那么遍历顺序应当先确定前面的数再确定后面的数,所以是从前到后遍历。
(5)举例推导dp数组:根据递推公式推导举例,如果发现结果不对,就把dp数组打印出来看看推导的数列是否一致。
代码还是很简单的,可以使用
70.爬楼梯:
五部曲上秤!
(1)确定dp数组以及下标的含义:dp[i]的定义为:爬到第i层楼,有dp[i]种方法
(2)递推公式:dp[i]有两个方向可以推出来,dp[i-1]和dp[i-2],这里理解是一个难点,为什么可以这样推导,因为只能走1步或者2步,而没有其他方法上一步到这一步。所以dp[i]=dp[i-1]+dp[i-2]。
(3)dp数组如何初始化:dp[1]=1,dp[2]=2
(4)确定遍历顺序:从前向后遍历
(5)举例推导:如果代码有问题就把dp数组打印出来看与自己的举例是否一样。
746.使用最小花费爬楼梯:
五部曲上秤!
(1)确定dp数组以及下标的含义:dp[i]的定义为到位置i所需要的花费是多少。
(2)递推公式:有两个途径得到dp[i],一个是dp[i-1],一个是dp[i-2],有一个难想的点就是,究竟是从dp[i-1]跳还是从dp[i-2]跳呢?根据题意是需要最小的,那么就是dp[i]=min[dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])。
(3)如何初始化:dp[0]=0, dp[1]=0
(4)遍历顺序:从前向后遍历
(5)举例推导
相关文章:

代码随想录算法训练营第38天 | 509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
代码随想录算法训练营第38天 | 509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯 理论基础自己看到题目的第一想法看完代码随想录之后的想法 链接: 509. 斐波那契数 链接: 70. 爬楼梯 链接: 746. 使用最小花费爬楼梯 理论基础 五部曲: 1.确定dp数组…...

变现实谈,我要的不是灵光一现,而是真实的实现!——感悟篇
变现要的是行动不是想法 正文时代奇点奇迹 点题以己及人 正文 每当我看到了一个有趣的事情 我会在脑中构思一些想法 会贴合我当下的想要做的事情 比如 在我写下这篇文章之前 我看到了 二战期间的诞生的一个奇迹 可口可乐 我就思考 咦 原来可口可乐居然是在这么个时间点成长…...

Matlab操作Excel筛选指定数据的对应数据
Matlab中在表格中寻找指定汉字,并返回其所在行数, 将该行数的另一列提取出来。 目录 一、前言 二、直接在命令行输出 三、保存筛选数据excel 一、前言 源数据excel: 指定汉子:买,得到下面数据: 二、直接…...

对于C++STL及其时间复杂度的总结
由于本次在山东CCPC邀请赛中,对于堆的时间复杂度记忆不清晰,导致第4题没有做出来,与铜牌失之交臂,故觉应整理STL的时间复杂度。 本文仅整理有用(竞赛)的stl及其用法,并且不阐述过于基础的内容。…...

Docker搭建FRP内网穿透服务器
使用Docker搭建一个frp内网穿透 在现代网络环境中,由于防火墙和NAT等原因,内网设备无法直接被外网访问。FRP (Fast Reverse Proxy) 是一款非常流行的内网穿透工具,它能够帮助我们将内网服务暴露给外网。本文将介绍如何在Linux服务器上使用Do…...

【NumPy】掌握NumPy的divide函数:执行高效的数组除法操作
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向…...
您的虚拟机未能继续运行,原因是遇到一个可纠正的错误。请保留挂起状态并纠正错误,或放弃挂起状态。
镜像:应急响应靶机 错误信息 此虚拟机的处理器所支持的功能不同于保存虑拟机状态的虚拟机的处理器所支持的功能。 从文件"E:\XXX.vmss"还原 CPU 状态时出错。 您的虚拟机未能继续运行,原因是遇到一个可纠正的错误。请保留挂起状态并纠正错误…...
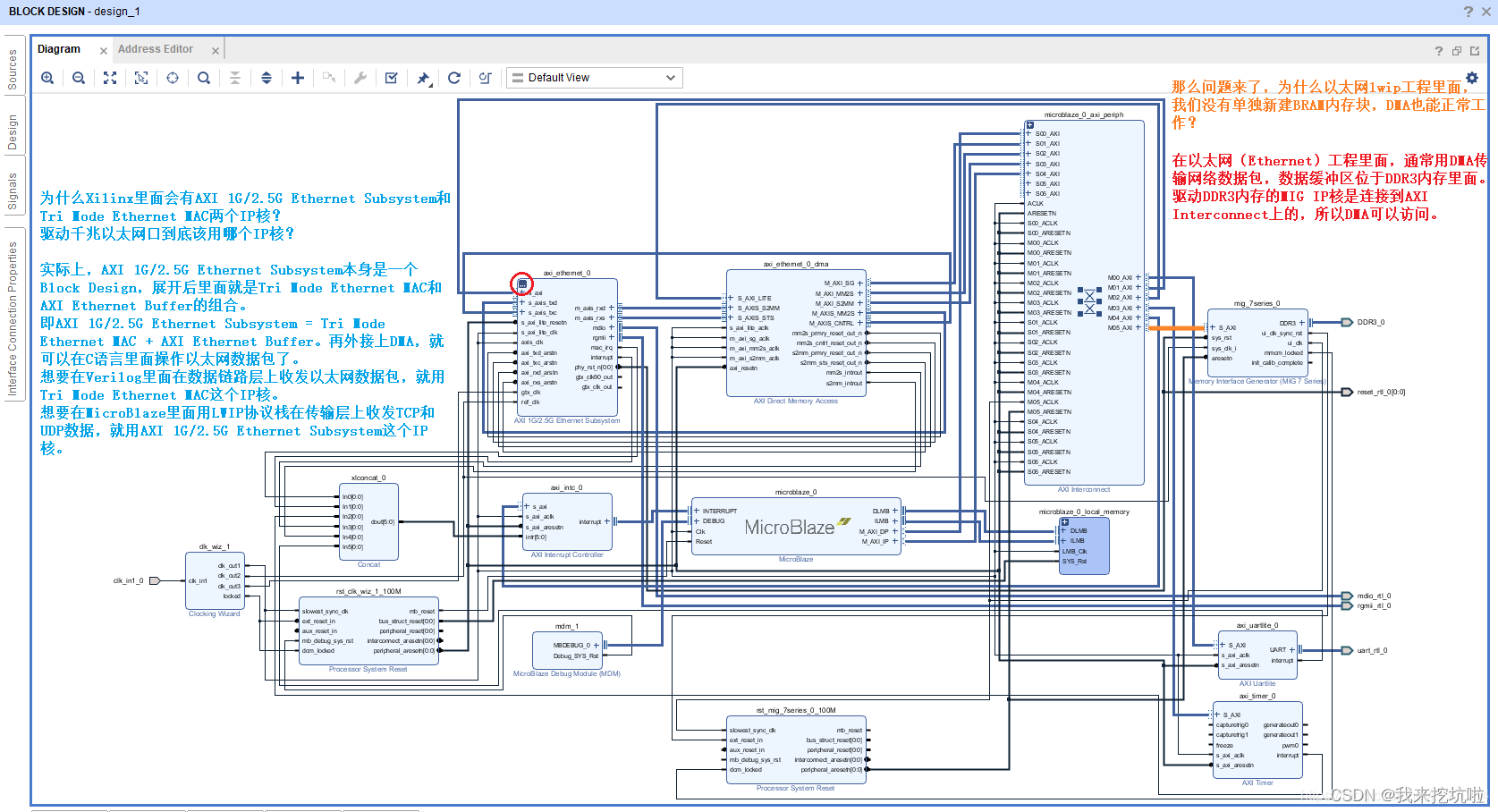
FPGA DMA IP核使用指南
摘要 本文旨在介绍FPGA中DMA(Direct Memory Access)IP核的使用,包括其基本框架、测试代码编写以及仿真波形的分析。DMA是一种允许外围设备直接与内存进行数据交换的技术,无需CPU的介入,从而提高了数据传输的效率。 1. 引言 在现代FPGA设计中,DMA IP核因其…...
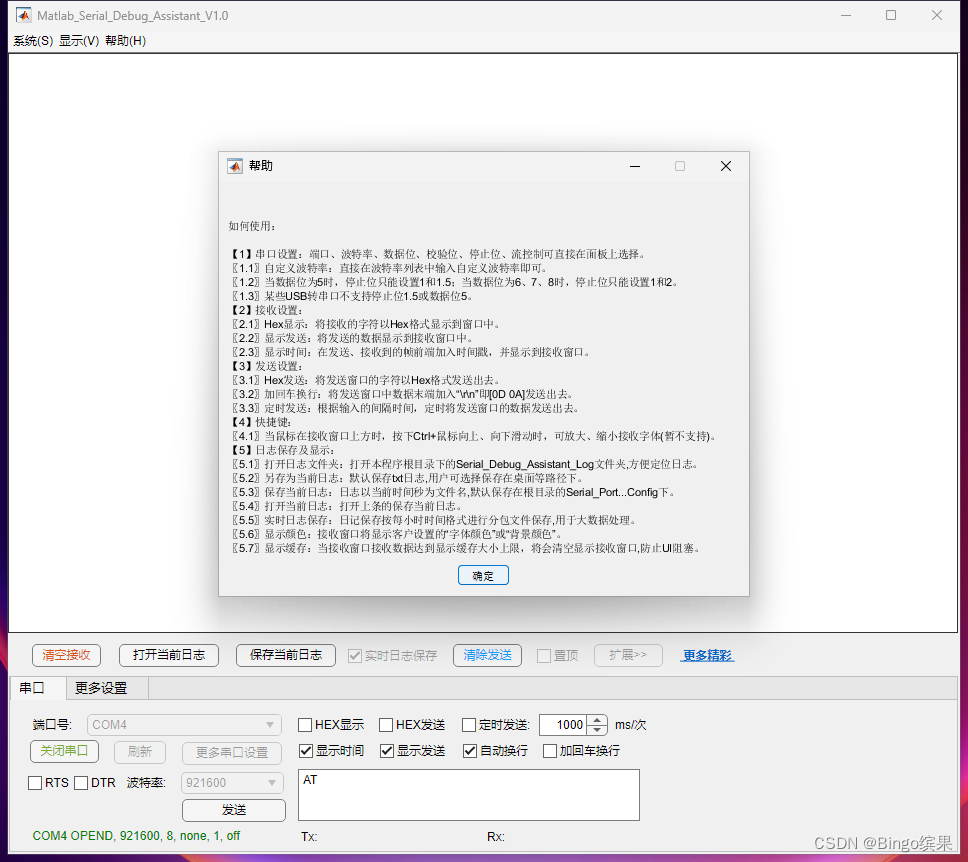
【博客20】缤果Matlab串口调试助手V1.0(中级篇)
超级好用的Matlab串口调试助手 开发工具: MATLAB 2024a中文版 (编程语言matlab) -> Matlab APP Designer 目录 前言 一、软件概要: 二、软件界面: 1.App演示 ---- ◇♣♡♠ ---- 2.其他扩展App展示 编辑 三、获取 >> 源码以及G…...

南京威雅学校:2024年度大戏《Tinkerbell(小叮当)》震撼落幕
三天连演三场 两小时十六幕高潮迭起的舞台故事 一百五十余名师生台前幕后全统筹 逾千名观众现场观演 四个城市五大平台同步直播 南京威雅2024年度大戏 《Tinkerbell(小叮当)》震撼落幕 它以商演级别的舞台设计 宏大而精密的舞台调度 直击心灵的…...

Kotlin 函数
文章目录 函数的定义函数的返回值参数默认值 & 调用时参数指定函数作用域Lambda 表达式匿名函数内联函数扩展函数中缀函数递归函数 & 尾递归函数 函数的定义 函数可以理解成一个小小的加工厂,给入特定的原材料,它就会给出特定的产品。 fun [接…...
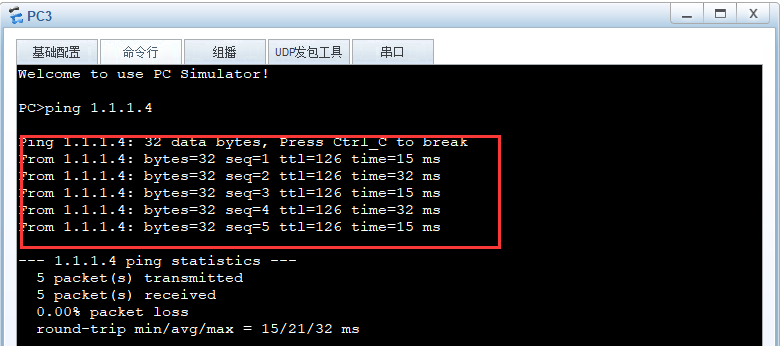
动态路由协议实验——RIP
动态路由协议实验——RIP 什么是RIP RIP(Routing Information Protocol,路由信息协议)是一种内部网关协议(IGP),是一种动态路由选择协议,用于自治系统(AS)内的路由信息的传递。RIP协议基于…...
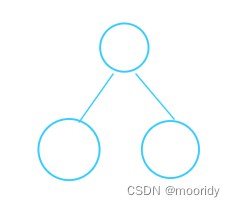
数据结构 | 二叉树(基本概念、性质、遍历、C代码实现)
1.树的基本概念 树是一种 非线性 的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点,称为根…...

很多Oracle中的SQL语句在EF中写不出来
很多复杂的Oracle SQL语句在Entity Framework(EF)中很难直接表达出来。虽然EF提供了一种方便的方式来使用C#代码查询和操作数据库,但它在处理某些复杂的SQL特性和优化时可能会有局限性。 以下是一些在EF中可能难以直接实现的Oracle SQL功能和…...

浏览器打开PHP文件弹出下载而不是运行代码
说明 使用phpstudy,极少会出现这种情况。 这里主要是帮助大家理解,为什么上传的木马不运行。 问题原因 首先需要理解,访问PHP文件弹出下载,说明服务端的容器(比如Apache或者Nginx)把文件当成了一个普通二…...

安卓自定义UI组件开发流程
安卓自定义ui组件开发流程 开发安卓自定义UI组件的流程大致可以分为以下几个步骤: 确定需求和设计: 确定需要自定义的UI组件的功能和外观。设计组件的交互逻辑和视觉效果。 创建自定义组件类: 创建一个新的Java类,继承自View、V…...
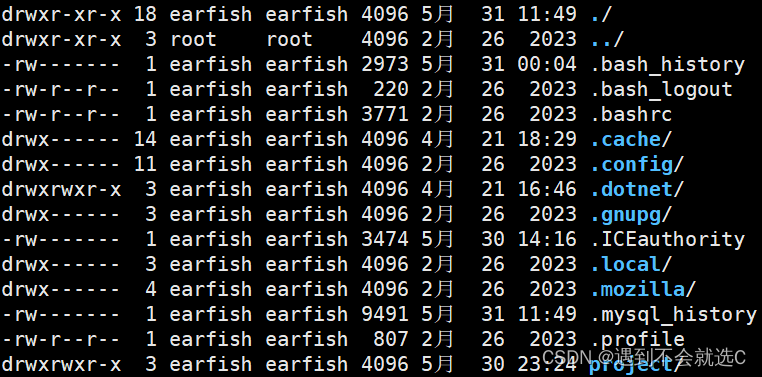
【LINUX】LINUX基础(目录结构、基本权限、基本命令)
文章目录 LINUX的目录结构LINUX的基本权限LINUX基本命令 LINUX的目录结构 /:表示根目录bin:存放二进制可执行文件(命令ls、cat、mkdir等)boot:存放系统引导文件dev:存放设备文件etc:存放系统配置文件home:…...

Aigtek功率放大器的主要性能要求有哪些
功率放大器是电子系统中的重要组件,用于将低功率信号放大到高功率水平。功率放大器的性能直接影响到信号的放大质量和系统的整体性能。下面西安安泰将介绍功率放大器的主要性能要求。 增益:功率放大器应当具有足够的增益,即将输入信号的幅度放…...
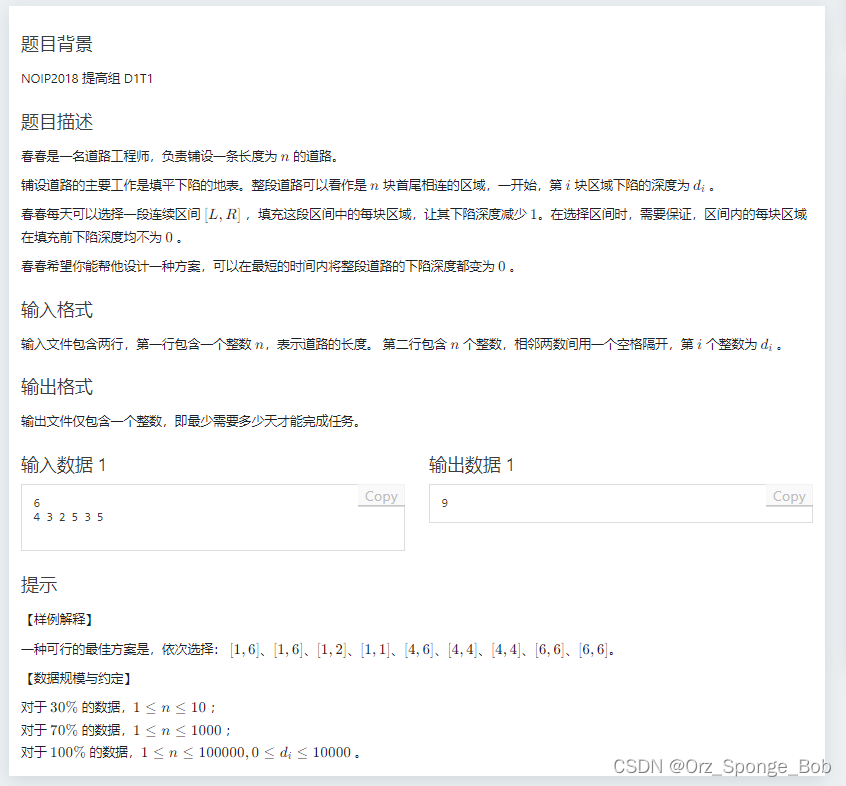
2024.5.29晚训参考代码
因为本套题没有BFS例题,所以我先把BFS模板放着 #include<bits/stdc.h> using namespace std; int n,m;//n*m的棋盘 int dis[402][402]; bool vis[402][402]; int X[]{-2,-2,-1,-1,1,1,2,2};//偏移量的表 int Y[]{-1,1,-2,2,-2,2,-1,1};//定义一个数组&…...
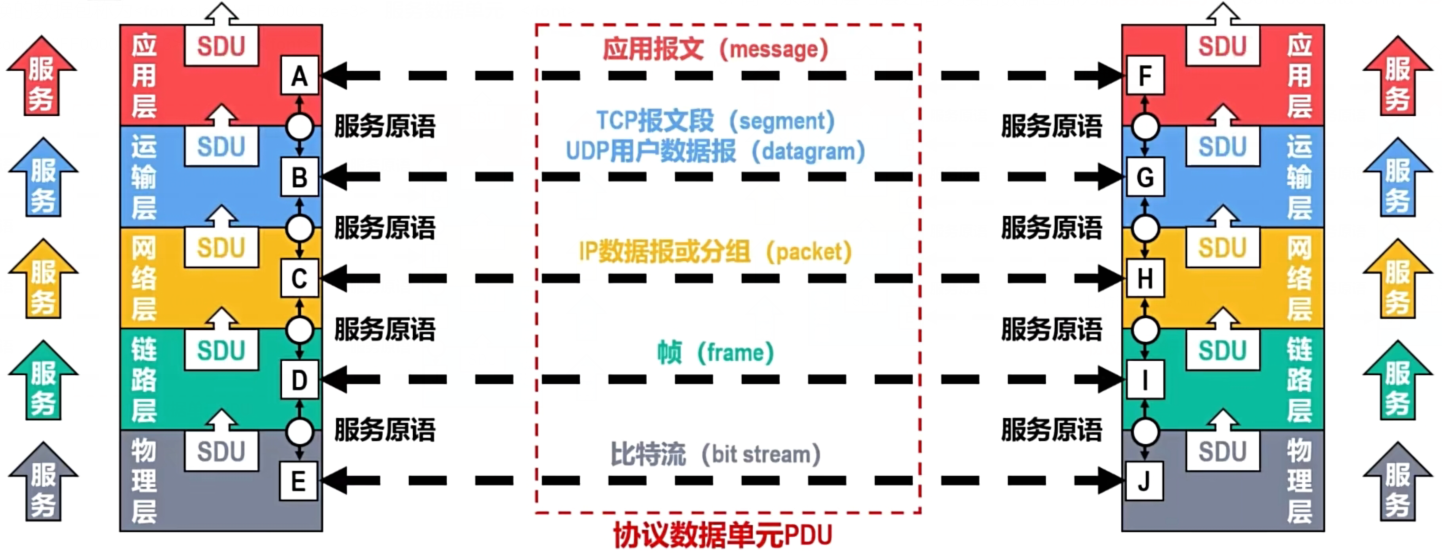
【计算机网络】——概述(图文并茂)
概述 一.信息时代的计算机网络二.互联网概述1.网络,互连网,互联网(因特网)1.网络2.互连网3.互联网(因特网) 2.互联网简介1.互联网发展的三个阶段2.互联网服务提供者(ISP)3.互联网的组…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
