【算法训练 day44 分割等和子集】
目录
- 一、分割等和子集-LeetCode 416
- 思路
- 实现代码
- 1.二维dp代码
- 2.一维dp代码
- 问题
- 总结
一、分割等和子集-LeetCode 416
Leecode链接: leetcode 416
文章链接: 代码随想录
视频链接: B站
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
思路
本体可以看作一个背包模型,将数组总和除2,将总和一半定义为背包的容量,数组元素为可选的物品。本题既可以定义一个一维dp数组,也可以定义一个二维dp数组,但二维便于理解与讲解并且一维只是二维的精简版,思想基本一致,所以主要写一下二维的思路。数组形式为dp[i][j],i为可选的物品范围,例如当i为3时,表示可选的物品范围为0到3下标的物品任意物品;j表示当前背包的容量大小。dp数组含义为,在j容量下,物品0到i范围可以获得的最大和。递推公式为dp[i][j] = dp[i-1][j]或dp[i][j] = max(dp[i-1][j] , dp[i-1][j-nums[i]] + nums[i])。前者表示不放的情况,后者表示物品放入后可能的情况。不放的条件就是背包容量不足以放下物品,放物品的条件就是当前背包的容量大于或等于当前物品的重量。
实现代码
1.二维dp代码
//cpp
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;int len = nums.size();//物品的数量for(int a:nums){sum += a;} if(sum%2 == 1) return false;int target = sum/2;//既是物品的价值也是物品的重量vector<vector<int>>dp(len,vector<int>(target+1,0));for(int j = nums[0];j<=target;j++){dp[0][j] = nums[0];}for(int i = 1;i<len;i++){for(int j = 0;j<=target;j++){if(j<nums[i]){dp[i][j] = dp[i-1][j];}else {dp[i][j] = max(dp[i-1][j],dp[i-1][j - nums[i]]+nums[i]);}}}if(dp[len-1][target] == target) return true;return false;}
};
2.一维dp代码
//cpp
class Solution {
public:bool canPartition(vector<int>& nums) {//vector<int> dp(10001, 0);int sum = 0;for(int a:nums){sum += a;} if(sum%2 == 1) return false;int t = sum/2;vector<int>dp(t+1,0);for(int i = 0;i<nums.size();i++){for(int j = t;j>=nums[i];j--){dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);}}if(dp[t] == t) return true;return false;}
};
问题
代码实现细节不熟练,比如初始化时,怎么将第一行的哪些数初始化为恒定值。
总结
一维与二维的区别在于:省去了多余空间的使用,并且改变了遍历顺序,这是因为如果跟二维数组一样从前往后遍历,就会导致重复选择同一个物品。比如,当i = 1时,dp[1] = 1、dp[2] = 1;当i = 2时,dp[1] = 1、dp[2] = 2,显然是不对的因为一件物品只能选一次。虽然一维省去了空间,但时间复杂很高,leetcode上一维dp的执行用时为300ms左右,空间占用达到了10MB左右;二维dp为100ms左右,同样的二维空间占用达到了98MB左右。
相关文章:

【算法训练 day44 分割等和子集】
目录 一、分割等和子集-LeetCode 416思路实现代码1.二维dp代码2.一维dp代码 问题总结 一、分割等和子集-LeetCode 416 Leecode链接: leetcode 416 文章链接: 代码随想录 视频链接: B站 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集&…...
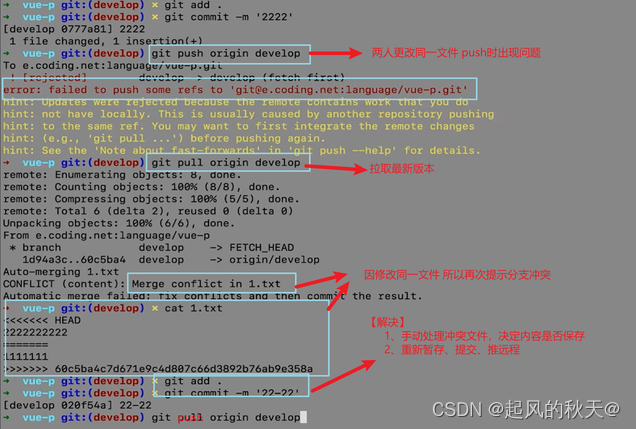
前端实习记录——git篇(一些问题与相关命令)
1、版本控制 (1)版本回滚 git log // 查看版本git reset --mixed HEAD^ // 回滚到修改状态,文件内容没有变化git reset --soft HEAD^ // 回滚暂存区,^的个数代表几个版本git reset --hard HEAD^ // 回滚到修改状态ÿ…...

XML Web 服务技术解析:WSDL 与 SOAP 原理、应用案例一览
XML Web服务是一种用于在网络上发布、发现和使用应用程序组件的技术。它基于一系列标准和协议,如WSDL、SOAP、RDF和RSS。下面是一些相关的内容: WSDL(Web服务描述语言):用于描述Web服务的基于XML的语言,定义…...

解析Java中1000个常用类:FunctionalInterface类,你学会了吗?
Java 8 引入了一系列新的特性和改进,其中之一便是函数式编程。函数式接口(Functional Interface)是函数式编程的核心概念之一。本文将深入探讨 FunctionalInterface 注解,介绍其用法、重要性,并通过示例展示如何在实际开发中应用函数式接口。 什么是函数式接口? 函数式…...

Kafka自定义分区器编写教程
1.创建java类MyPartitioner并实现Partitioner接口 点击灯泡选择实现方法,导入需要实现的抽象方法 2.实现方法 3.自定义分区器的使用 在自定义生产者消息发送时,属性配置上加入自定义分区器 properties.put(ProducerConfig.PARTITIONER_CLASS_CONFIG,&q…...

python移动文件
测试1(直接把B文件夹移动到了A里,成为了A的子文件夹) import os import shutil# 移动文件夹,B文件夹在当前目录没有了,跑到了A的子文件里 ## shutil.move(./example1/B/, ./example1/A/)测试2(B文件不动,将B文件里的所有的子文件夹移动到A内…...
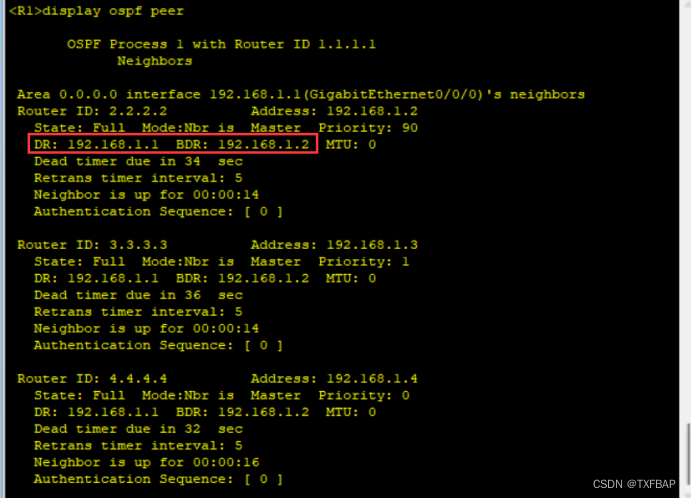
eNSP学习——OSPF的DR与BDR
目录 相关命令 原理概述 实验内容 实验目的 实验拓扑 实验编址 实验步骤 1、基本配置 2、搭建基本的OSPF网络 3、查看默认情况下的DR/BDR状态 4、根据现网需求影响DR/BDR选举 相关命令 [R4]int g0/0/0 [R4-GigabitEthernet0/0/0]ospf network-type p2mp //在接…...
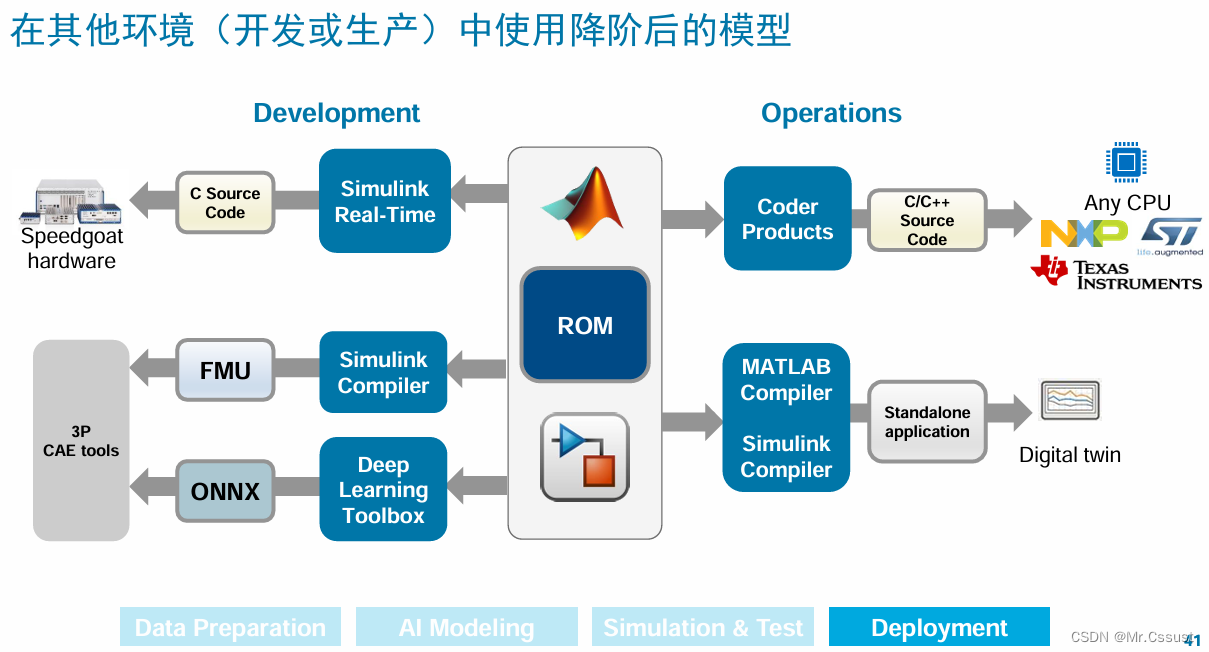
【文献阅读】应用人工智能在Simulink中开发软件
参考文献:《AI用于Simulink模型的降阶方法和应用场景》Mathworks在2024年MATLAB XEPO大会的演讲 文章目录: 1、模型框架 2、数据准备 3、AI建模 4、仿真和测试 5、部署应用 Tips:降阶模型(Reduced Order Modeling࿰…...

【计算机毕设】基于SpringBoot的房产销售系统设计与实现 - 源码免费(私信领取)
免费领取源码 | 项目完整可运行 | v:chengn7890 诚招源码校园代理! 1. 研究目的 随着房地产市场的发展和互联网技术的进步,传统的房产销售模式逐渐向线上转移。设计并实现一个基于Spring Boot的房产销售系统࿰…...
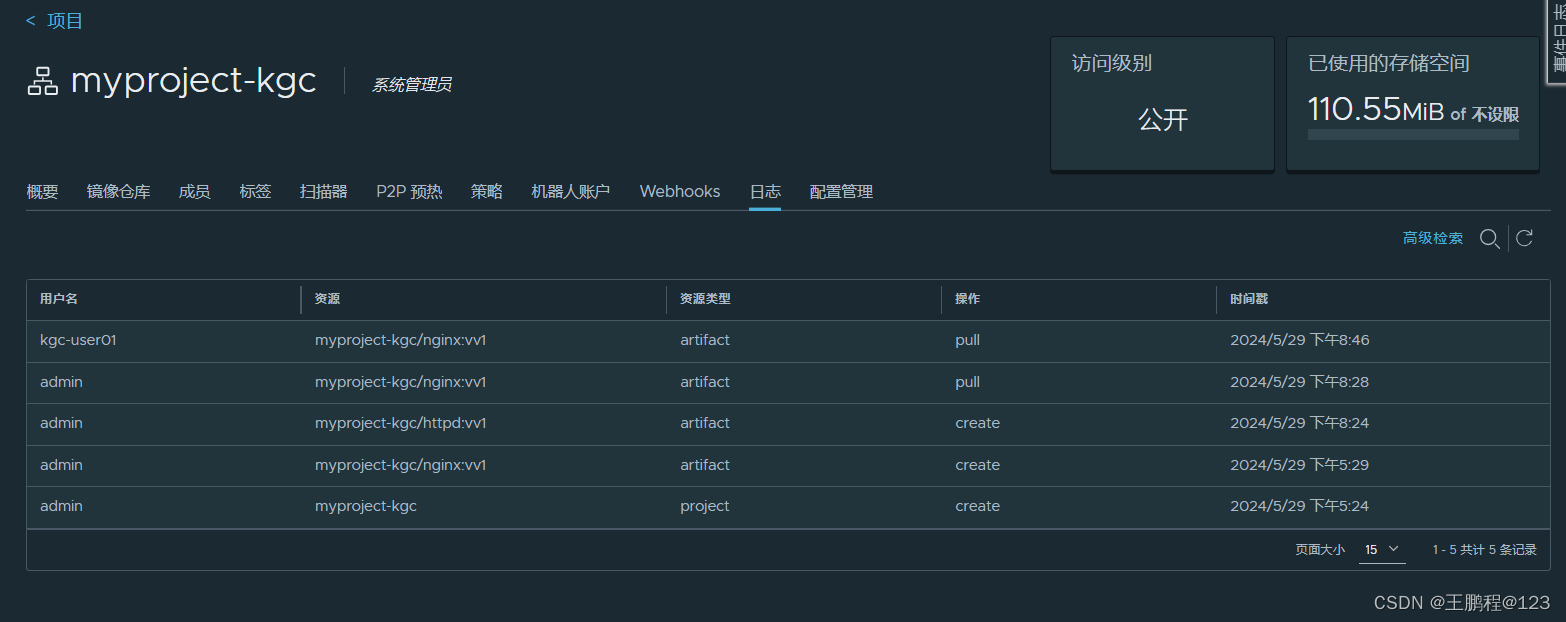
Docker 私有仓库部署和管理
目录 一、案例一 概述 二、案例一 前置知识点 2.1、什么是 Docker Compose 2.2、什么是 Consul 三、案例一 使用 docker Compose 搭建 Consul 集群环境 3.1、案例实验环境 3.2、案例需求 四、案例实施 4.1、Docker 网络通信 1)端口映射 2…...
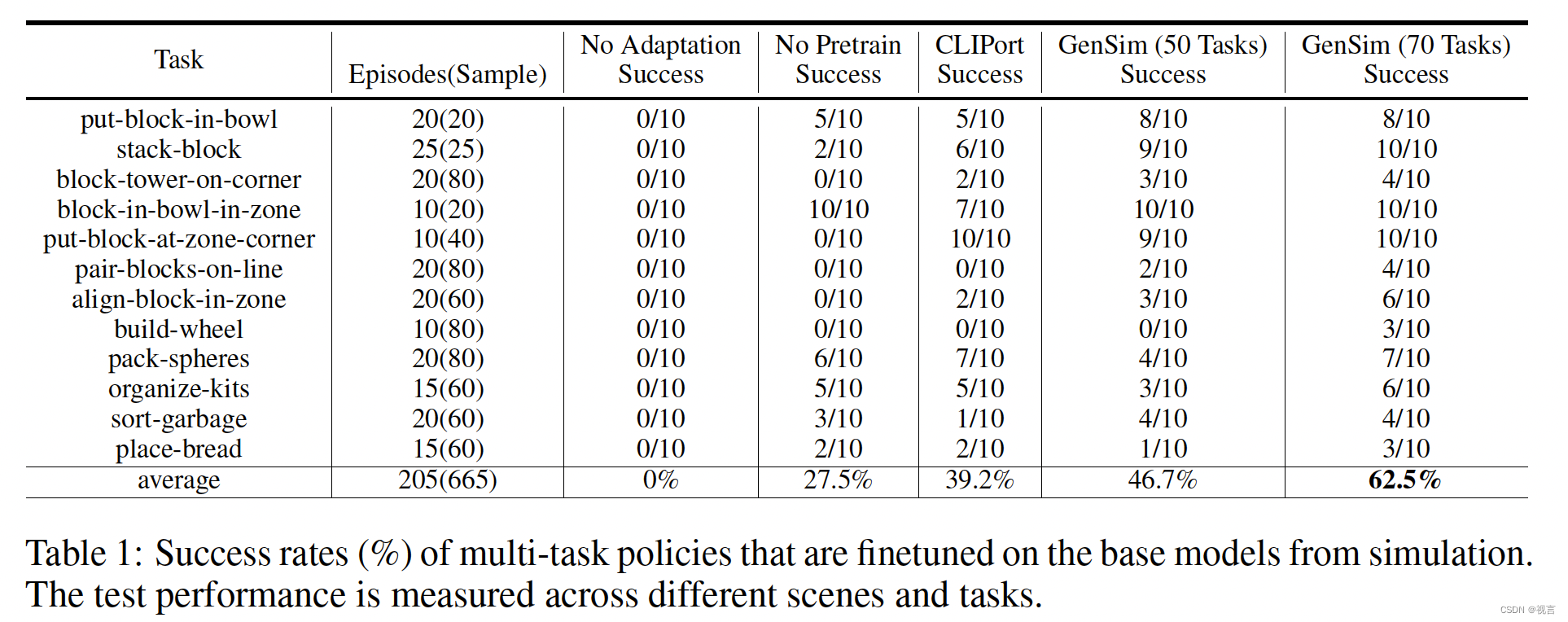
大模型时代的具身智能系列专题(六)
UCSD 王小龙组 王小龙是UCSD电子与计算机工程系的助理教授。他曾在加州大学伯克利分校与Alexei Efros和Trevor Darrell一起担任博士后研究员,在CMU RI获得了机器人学博士学位,师从Abhinav Gupta。他的研究重点是通过视频和物理机器人交互数据来学习3D和…...
Pytorch入门需要达到的效果
会搭建深度学习环境和依赖包安装 使用Anaconda创建环境、在pytorch官网安装pytorch、安装依赖包 会使用常见操作,例如matmul,sigmoid,softmax,relu,linear matmul操作见文章torch.matmul()的用法 sigmoid࿰…...
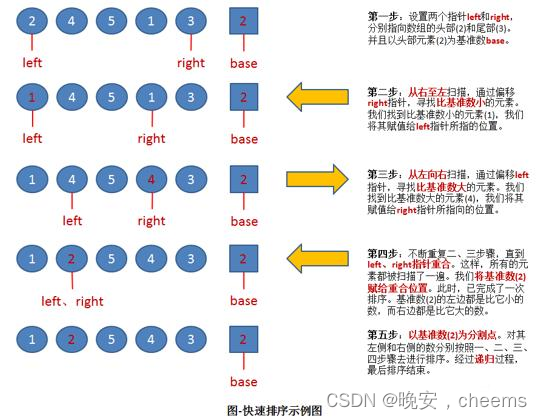
数据结构的快速排序(c语言版)
一.快速排序的概念 1.快排的基本概念 快速排序是一种常用的排序算法,它是基于分治策略的一种高效排序算法。它的基本思想如下: 从数列中挑出一个元素作为基准(pivot)。将所有小于基准值的元素放在基准前面,所有大于基准值的元素放在基准后面。这个过程称为分区(partition)操作…...
)
数据结构基础篇(4)
十六.循环链表 概念 循环链表是一种头尾相接的链表(最后一个结点的指针域指向头结点,整个链表形成一个环)优点 从表任一结点出发均可找到表中其他结点判断终止 由于循环链表中没有NULL指针,所以涉及遍历操作时,终止条…...
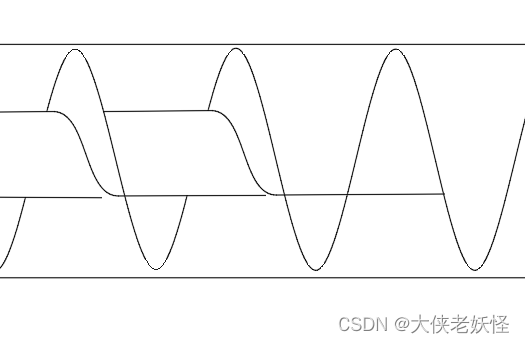
使用cad绘制一个螺旋输送机
1、第一步,绘制一个矩形 2、使用绘图中的样条线拟合曲线,绘制螺旋线。 绘制时使用上下辅助线、阵列工具绘制多个竖线保证样条线顶点在同一高度。 3、调整矩形右侧的两个顶点,使其变形。 矩形1和矩形2连接时,使用blend命令&#…...

迭代器模式(行为型)
目录 一、前言 二、迭代器模式 三、总结 一、前言 迭代器模式(Iterator Pattern)是一种行为型设计模式,提供一种方法顺序访问一个聚合对象中各个元素,而又不暴露该对象的内部表示。总的来说就是分离了集合对象的遍历行为,抽象出…...
Django——Admin站点(Python)
#前言: 该博客为小编Django基础知识操作博客的最后一篇,主要讲解了关于Admin站点的一些基本操作,小编会继续尽力更新一些优质文章,同时欢迎大家点赞和收藏,也欢迎大家关注等待后续文章。 一、简介: Djan…...

React 组件通信
1.从父组件向子组件传递参数: 父组件可以通过props将数据传递给子组件。子组件通过接收props来获取这些数据。 // 父组件 const ParentComponent () > {const data Hello, Child!;return <ChildComponent childData{data} />; }; // 子组件 const ChildCompone…...
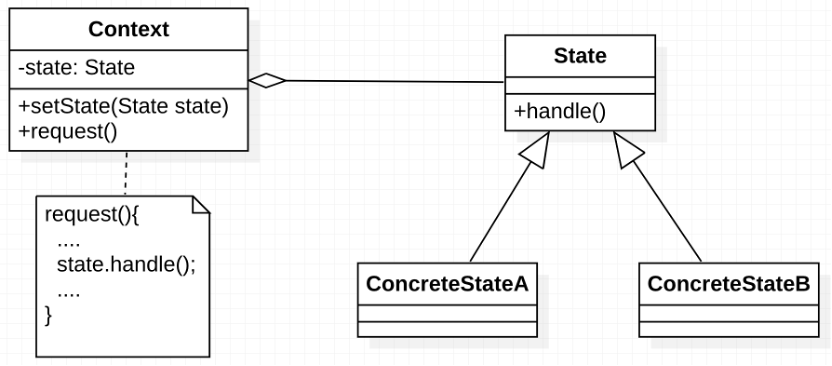
【再探】设计模式—访问者模式、策略模式及状态模式
访问者模式是用于访问复杂数据结构的元素,对不同的元素执行不同的操作。策略模式是对于具有多种实现的算法,在运行过程中可动态选择使用哪种具体的实现。状态模式是用于具有不同状态的对象,状态之间可以转换,且不同状态下对象的行…...

新人硬件工程师,工作中遇到的问题list
新人硬件工程师能够通过面试,已经证明是能够胜任硬件工程师职责,当然胜任的时间会延迟,而不是当下,为什么呢?因为学校学习和公司做产品,两者之间有差异,会需要适应期。今天来看看新人硬件工程师…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
