数据结构学习笔记
1. 数组 (Array)
定义
数组是一种线性数据结构,用于存储固定大小的相同类型元素集合。每个元素都有一个索引,用于快速访问。
特点
- 优点:访问速度快,通过索引直接访问O(1)时间复杂度。
- 缺点:大小固定,插入和删除元素效率低(需移动后续元素)。插入元素的时间复杂度为O(n),删除元素的时间复杂度同样为O(n)。
应用场景
适合于元素数量固定且频繁查询的场景,如排序数组、查找表等。多维数组常用于表示矩阵、图像、游戏地图等需要多个维度来描述的数据结构。
2. 链表 (Linked List)
定义
链表是一种由节点组成的数据结构,每个节点包含存储数据的部分以及指向下一个节点的指针。通过节点之间的指针连接,形成了链表的结构。链表可以分为单链表、双向链表和循环链表等不同类型,它们各自具有特定的特点和应用场景。
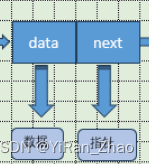
- 数据元素:节点存储的实际数据。数据可以是任意类型,例如整数、字符、字符串、对象等。
- 指针(或引用):指向下一个节点的指针。它存储了下一个节点在内存中的地址,通过这个指针可以找到链表的下一个节点。
类型
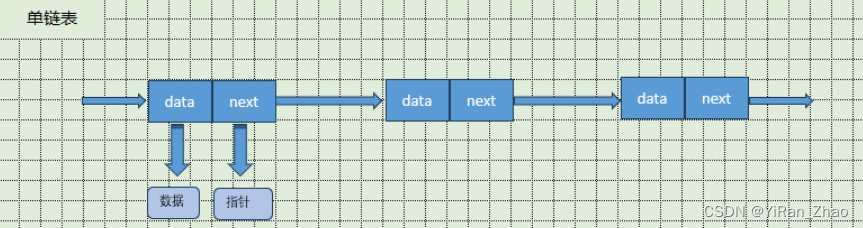
单向链表
- 单链表是最简单的链表类型,每个节点包含一个数据元素和一个指向下一个节点的指针。单链表的尾节点指针为空,表示链表的结束。单链表的插入、删除操作相对简单高效,但随机访问的效率较低。
单向链表的特点
- 非连续存储:单链表中的节点在内存中可以是任意位置,不要求连续存储。每个节点通过指针指向下一个节点,从而将它们连在一起。
- 动态性:相较于数组,单链表的长度可以动态地增减,不需要预先分配内存空间。这使得单链表在需要频繁插入和删除节点的场景中更加灵活。
- 搜索效率相对较低:由于单链表的节点只能通过指针一个一个地遍历,因此搜索某个特定的节点需要遍历整个链表,时间复杂度为O(n),其中n是链表的长度。相比之下,数组可以使用索引直接访问元素,搜索效率更高。
- 内存空间的额外开销:单链表中的每个节点除了存储数据外,还需要存储下一个节点的指针,这导致了额外的内存开销。
- 插入和删除效率较高:相对于数组,单链表在插入和删除节点时效率较高。插入一个节点只需要改变相邻节点的指针,而删除一个节点只需要改变前一个节点的指针指向下一个节点,不需要移动其他元素。
- 灵活性:单链表可以方便地进行节点的插入和删除操作,可以根据实际需要进行自由调整。
双向链表
- 每个节点包含数据、指向前一个节点和指向下一个节点的指针。

双向链表的特点
- 支持双向遍历:相对于单向链表,双向链表支持双向遍历,可以从前往后、从后往前遍历链表。
- 插入、删除节点效率更高:相较于单向链表,双向链表在插入和删除某个节点时,只需要改变相邻两个节点的指向,效率更高,尤其是在删除链表中某个元素时更加便捷。
- 需要更多的内存空间:相比单向链表,双向链表需要更多的内存空间来存储额外的指针,增加了额外的空间开销。
- 内存存储不连续:相对于数组,链表中节点的内存存储位置不连续,需要使用指针进行串联,这可以更加灵活地进行插入、删除和移动节点的操作。
- 操作复杂度较高:插入、删除、移动等操作,需要修改前后节点的指针信息,操作比较繁琐。
循环链表
- 链表的最后一个节点指向链表的第一个节点,形成闭环。

循环链表特点
- 首位相连:循环链表的最后一个节点指向链表的第一个节点,使得链表成为一个环形结构。这样,链表的结束节点与开始节点相连,可以实现无限循环,更加灵活和方便。
- 操作始终成立:由于循环链表始终是一个环形的结构,因此操作(例如插入、删除、查找等)始终处于链表中,这也保证了操作始终能够完成。
- 遍历循环:与单向链表相比,在遍历时需要注意指针不要陷入死循环。否则会导致遍历永远无法结束。
- 内存空间的额外开销:与单向链表相比,循环链表需要多一个指向头部节点的指针,增加了额外的空间开销。
- 插入和删除效率较高:相对于数组,循环链表在插入和删除节点时效率比较高。插入一个节点时只需要修改相邻节点的指针即可,而删除一个节点时只需要改变前一个节点的指针指向下一个节点即可。
优缺点
- 优点:动态分配内存,插入和删除操作快(O(1),只需改变指针)。
- 缺点:访问速度慢,需从头节点遍历(最坏情况下O(n))。
应用场景
适用于频繁插入和删除操作的场景,如实现堆栈、队列等。
3. 栈 (Stack)
定义
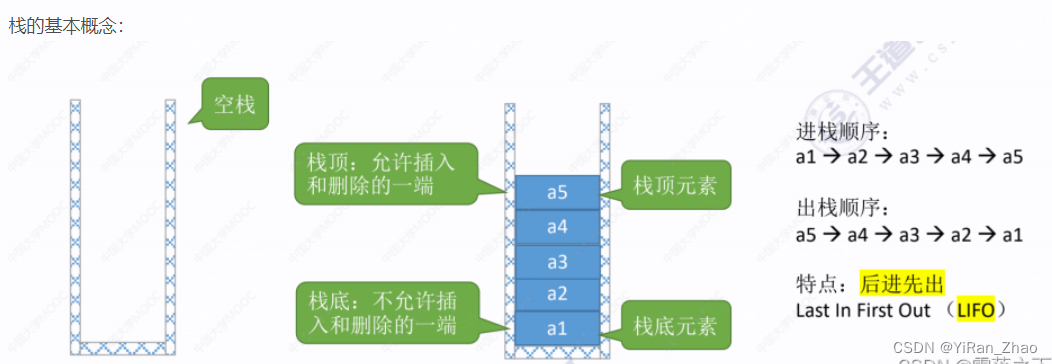
栈是一种特殊的线性结构,遵循后进先出(LIFO, Last In First Out)原则。只允许在一端(栈顶)进行插入和删除操作。
操作
- 压栈(Push):在栈顶添加元素。
- 弹栈(Pop):移除栈顶元素。
- 栈的插入和删除操作只能在栈顶进行,因此栈是一个只能从一端访问的数据结构。
应用场景
回溯算法、函数调用栈、括号匹配等。
4. 队列 (Queue)
定义
队列是一种线性结构,遵循先进先出(FIFO, First In First Out)原则。一端添加元素(队尾),另一端移除元素(队头)。
操作
- 入队(Enqueue):在队尾添加元素。
- 出队(Dequeue):从队头移除元素。
应用场景
任务调度、缓冲区管理等。
栈和队列的对比:
结构:栈和队列都是线性结构,但栈只有一个入口(栈顶)和一个出口(栈顶),而队列有一个入口(队尾)和一个出口(队头)。
插入和删除操作:栈的插入和删除操作只能在栈顶进行,而队列的插入操作在队尾进行,删除操作在队头进行。
访问顺序:栈按照后进先出的顺序访问元素,而队列按照先进先出的顺序访问元素。
应用场景:栈常用于函数调用、表达式求值、回溯算法等场景,而队列常用于任务调度、消息传递、缓冲区管理等场景。
5. 哈希表 (Hash Table)
定义
哈希表是一种通过哈希函数将键(Key)直接映射到值(Value)的数据结构,提供了快速的查找、插入和删除操作。
哈希表的实现就是映射函数构造,哈希表的映射函数构造方法也有很多,常见的有:直接定址法、 除留余数法、 乘余取整法、 数字分析法、 平方取中法、 折叠法、 随机数法等。
特点
- 优点:平均时间复杂度为O(1)。
- 缺点:可能遇到哈希冲突,需要解决冲突策略(如开放寻址法、链地址法)。
应用场景
字典、缓存、数据库索引等。
6. 树 (Tree)
定义
树是一种分层的非线性数据结构,由节点(Node)和边(Edge)组成,每个节点有零个或多个子节点,且只有一个根节点。
- 树是由一个或多个节点(或称为顶点)的有限集合构成。
- 在任何非空树中,存在唯一一个称为根(Root)的节点,没有父节点。
- 除根节点外的每个节点都有一个父节点。
- 每个节点可以有零个或多个子节点(子树)。
- 树中的节点形成一种层次关系,没有环路(即节点之间不存在重复路径)。
- 子树之间相互独立,即任意两个子树的节点集合不会相交。
基本术语
- 节点(Node):树中的基本单位,存储数据元素。
- 边(Edge):连接树中节点的链接,表示父子关系。
- 根节点(Root Node):没有父节点的节点。
- 叶节点(Leaf Node):没有子节点的节点。
- 子节点(Child Node):某个节点的直接下一级节点。
- 父节点(Parent Node):直接位于某节点之上的节点。
- 兄弟节点(Sibling Node):具有相同父节点的节点。
- 度(Degree):节点的子节点数目。
- 层次(Level):从根开始到某个节点的距离,根节点处于第0层。
- 高度(Height):树中节点的最大层次数。
操作
- 创建树:初始化一个空树或构造指定结构的树。
- 插入节点:在树的指定位置添加新节点。
- 删除节点:移除树中的某个节点并保持树的特性。
- 查找节点:在树中搜索特定值的节点。
- 遍历树:按照某种顺序访问树中的所有节点,常见的遍历方法有前序遍历、中序遍历、后序遍历和层序遍历。
特殊类型的树
- 二叉树:每个节点最多有两个子节点的树。
- 二叉搜索树(BST):二叉树的一种,左子树所有节点的值小于其父节点,右子树所有节点的值大于其父节点。
- 平衡二叉树(如AVL树、红黑树):自平衡的二叉搜索树,确保树的高度大致保持对数级别。
- B树、B+树:适用于文件系统和数据库索引的自平衡树。
- 堆:一种完全二叉树,常用于优先队列实现。
应用场景
- 文件系统、数据库索引、表达式解析等。
7. 图 (Graph)
定义
图是由顶点(Vertex)和边(Edge)组成的非线性数据结构,边可以连接任意两个顶点,形成更复杂的关系网络。
类型
- 有向图 / 无向图
- 加权图 / 非加权图
应用场景
社交网络、地图导航、网络路由等。
相关文章:

数据结构学习笔记
1. 数组 (Array) 定义 数组是一种线性数据结构,用于存储固定大小的相同类型元素集合。每个元素都有一个索引,用于快速访问。 特点 优点:访问速度快,通过索引直接访问O(1)时间复杂度。缺点:大小固定,插入…...

vscode导入自定义模块报错ModuleNotFoundError解决方案
问题描述 我的项目为great_gas_or_agents,目录结构如下: log_data_extract main.py math_algorithm 现在我运行main.py,报错:from math_algorithm.utils import parse_month_match_request,ModuleNotFoundError: No …...

go mod包管理与应用,常见错误排查方法
go mod包管理 go 中 包管理使用go mod 进行包管理 go mod init 项目名称 go mod init myproject_go生成的go.mod中有 module myproject_go 创建目录go_service 其下有两个go文件,go_request.go go_write.go . 根目录下有main.go入口文件。于是项目结构类似于&…...

数据结构作业
第1章 绪论 单选题 数据在计算机的存储器中表示时,逻辑上相邻的两个元素对应的物理地址也是相邻的,这种存储结构称之为________。 B. 顺序存储结构 算法指的是________。 D. 求解特定问题的指令有限序列 下面程序段的时间复杂度为:_______…...
项目纪实 | 版本升级操作get!GreatDB分布式升级过程详解
某客户项目现场,因其业务系统要用到数据库新版本中的功能特性,因此考虑升级现有数据库版本。在升级之前,万里数据库项目团队帮助客户在本地测试环境构造了相同的基础版本,导入部分生产数据,尽量复刻生产环境进行升级&a…...

富格林:应用正规技巧阻挠被骗
富格林悉知,随着如今入市现货黄金的朋友愈来愈多,不少投资者也慢慢开始重视起提高自身的正规投资技巧,希望能阻挠被骗更高效地在市场上获利。虽然目前黄金市场存在一定的受害风险,但只要投资者严格按照正规的交易规则来做单&#…...
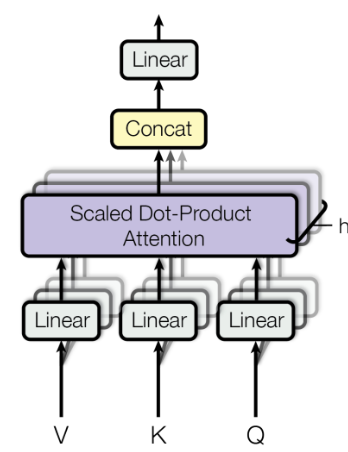
【模型架构】学习RNN、LSTM、TextCNN和Transformer以及PyTorch代码实现
一、前言 在自然语言处理(NLP)领域,模型架构的不断发展极大地推动了技术的进步。从早期的循环神经网络(RNN)到长短期记忆网络(LSTM)、Transformer再到当下火热的Mamba(放在下一节&a…...
【LeetCode】38.外观数列
外观数列 题目描述: 「外观数列」是一个数位字符串序列,由递归公式定义: countAndSay(1) "1"countAndSay(n) 是 countAndSay(n-1) 的行程长度编码。 行程长度编码(RLE)是一种字符串压缩方法,…...
)
如何解决Ubuntu中软件包安装时的404错误(无法安装gdb、cgddb等)
目录 问题描述 解决方法 1. 更新软件包列表 2. 使用--fix-missing选项 3. 更换软件源 4. 清理和修复包管理器 总结 在使用Ubuntu进行软件包安装时,有时可能会遇到404错误。这种错误通常是由于软件源中的某些包已经被移除或迁移到其他位置。本文将介绍几种解决…...
SpringBoot中MyBatisPlus的使用
MyBatis Plus 是 MyBatis 的增强工具,提供了许多强大的功能,简化了 MyBatis 的使用。下面是在 Spring Boot 中使用 MyBatis Plus 的步骤: 添加依赖:在 Maven 或 Gradle 的配置文件中添加 MyBatis Plus 的依赖。 配置数据源&#…...

前后端交互:axios 和 json;springboot 和 vue
vue 准备的 <template><div><button click"sendData">发送数据</button><button click"getData">接收</button><button click"refresh">刷新</button><br><ul v-if"questions&…...
)
前端技术专家岗(虚拟岗)
定位: 团队技术负责人、技术领导者;确保框架、工具的低门槛、高性能、可扩展; 素质要求: 具备架构设计能力;一个或者多个领域的技术专家;较为丰富的基础建设经验;项目管理能力、任务分解、协…...
redis windows环境下的部署安装
2024Redis windows安装、部署与环境变量 一、下载 Redis官网目前暂不支持Windows版本,只能从github中下载。 windows 64位系统下载redis路径:https://github.com/tporadowski/redis/releases,下载zip包。 目前Windows版本只更新到5.0的版本…...
大字体学生出勤记录系统网页HTML源码
源码介绍 上课需要一个个点名记录出勤情况,就借助AI制作了一个网页版学生出勤记录系统, 大字体显示学生姓名和照片,让坐在最后排学生也能看清楚,显示姓名同时会语音播报姓名, 操作很简单,先导入学生姓名…...

筛斗数据提取技术在企业成本预测中的应用
在当今的商业环境中,准确的成本预测对于企业的财务健康和战略规划至关重要。随着大数据和人工智能技术的飞速发展,数据提取技术已经成为企业进行成本预测的强大工具。本文将探讨数据提取技术如何帮助企业进行成本预测,并分析其对企业决策过程…...

enum编程入门:探索枚举类型的奥秘
enum编程入门:探索枚举类型的奥秘 在编程的世界里,enum(枚举)类型是一种特殊的数据类型,它允许我们为变量设置一组预定义的、有限的值。这种类型在很多编程语言中都得到了广泛的应用,为开发者提供了更加清…...
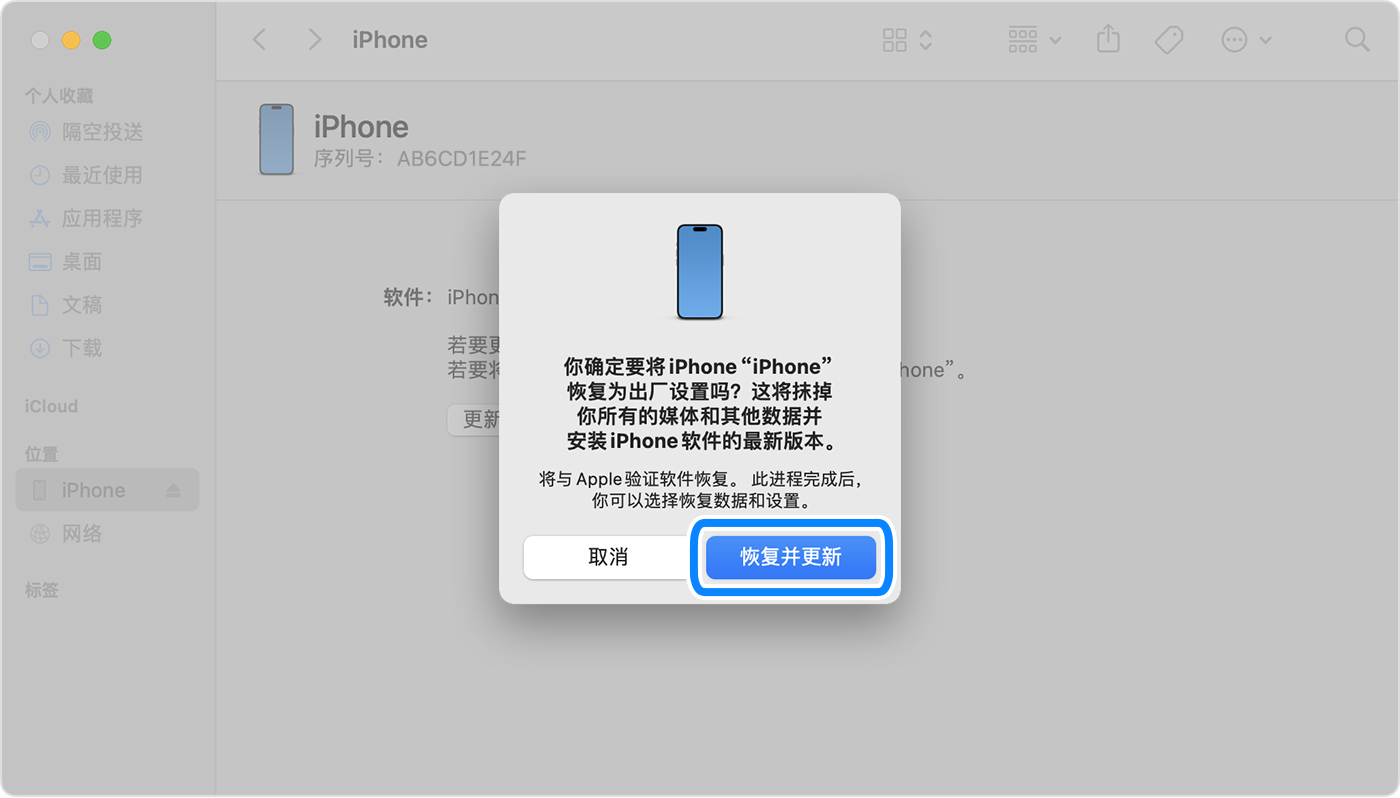
刷机 iPhone 进入恢复模式
文章目录 第 1 步:确保你有一台电脑(Mac 或 PC)第 2 步:将 iPhone 关机第 3 步:将 iPhone 置于恢复模式第 4 步:使用 Mac 或 PC 恢复 iPhone需要更多协助? 本文转载自:如果你忘记了 …...

计算属性和侦听器:为什么在某些情况下使用计算属性比使用methods更好,如何使用侦听器来监听数据的变化。
计算属性和methods的区别和使用场景 计算属性(Computed properties)是 Vue 中非常重要的一个功能,它有以下的优点: 数据缓存:计算属性基于它们的依赖进行缓存。只有在相关依赖发生变化时,才会重新求值。这…...

一文带你搞懂大事务的前因后果
引言 一文带你搞懂Spring事务上篇文章介绍了Spring事务相关内容,本文主要介绍业务开发中遇到的大事务问题。 https://github.com/WeiXiao-Hyy/blog 整理了Java,K8s,极客时间,设计模式等内容,欢迎Star! 什么是大事务 运行时间(调用远程事务或…...
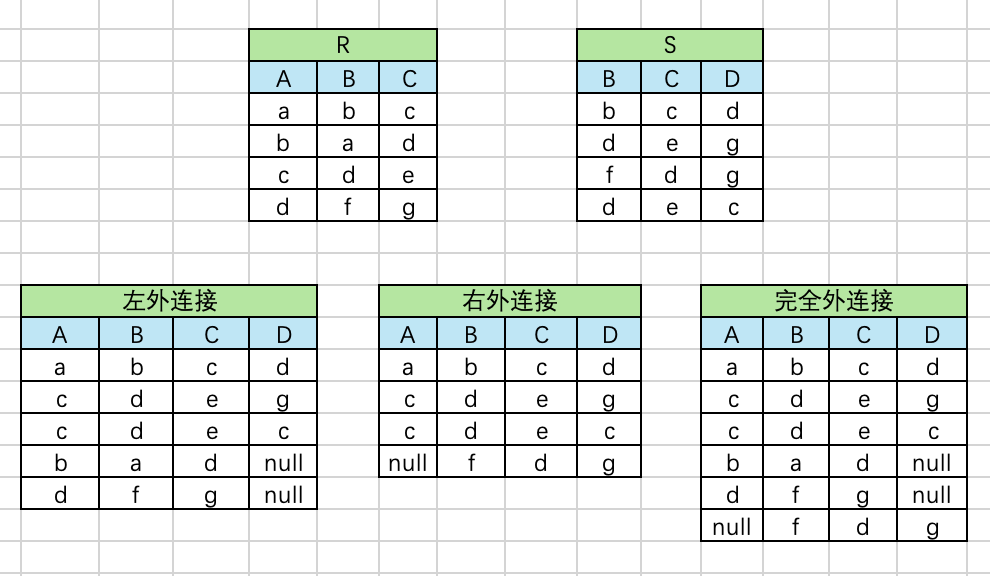
关系数据库:关系运算
文章目录 关系运算并(Union)差(Difference)交(Intersection)笛卡尔积(Extended Cartesian Product)投影(projection)选择(Selection)除…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...

在ubuntu等linux系统上申请https证书
使用 Certbot 自动申请 安装 Certbot Certbot 是 Let’s Encrypt 官方推荐的自动化工具,支持多种操作系统和服务器环境。 在 Ubuntu/Debian 上: sudo apt update sudo apt install certbot申请证书 纯手动方式(不自动配置)&…...

项目研究:使用 LangGraph 构建智能客服代理
概述 本教程展示了如何使用 LangGraph 构建一个智能客服代理。LangGraph 是一个强大的工具,可用于构建复杂的语言模型工作流。该代理可以自动分类用户问题、分析情绪,并根据需要生成回应或升级处理。 背景动机 在当今节奏飞快的商业环境中,…...
