长城电脑压缩文件丢失了怎么办？怎么解决
在数字化时代，电脑已成为我们日常生活和工作中不可或缺的设备。长城电脑作为国内知名品牌，以其稳定可靠的性能赢得了广大用户的信赖。然而，即便是可靠的电脑，也难免会遇到一些问题。其中，压缩文件丢失无疑是一个令人头疼的难题。本文将围绕这一问题，探讨其可能的原因，并提供相应的解决方案，希望帮助长城电脑用户快速恢复丢失的压缩文件。
一、长城电脑压缩文件丢失的可能原因
误删除：在整理文件时，可能不小心将压缩文件删除。
病毒感染：电脑遭受病毒攻击，病毒可能破坏或删除压缩文件。
硬盘故障：硬盘出现故障或损坏，导致存储的压缩文件丢失。
软件问题：压缩软件本身存在漏洞或错误，导致文件丢失。
二、长城电脑压缩文件丢失怎么解决
当我们发现长城电脑上的压缩文件丢失时，首先不要慌张，可以参考以下五种方法进行恢复。
方法1：回收站恢复
长城电脑压缩文件丢失怎么找回？可检查电脑回收站，看是否可以将误删除的压缩文件恢复。
1、打开电脑桌面的“回收站”图标。
2、在回收站中，查找丢失的压缩文件，根据文件名或文件类型等进行筛选。
3、选中需要恢复的文件，右键点击选择“还原”，文件将被恢复到原来的位置。
温馨提示：如果您的文件是通过shift+delete删除的，或者回收站已被清空，此方法将不再适用。
方法2：备份恢复
长城电脑压缩文件丢失了怎么办？如果之前对文件进行了备份，可以从备份中恢复丢失的压缩文件。
1、打开之前设置的备份存储位置，如外部硬盘、云存储等。
2、在备份中找到对应的文件夹或文件，确保其包含丢失的压缩文件。
3、将备份中的压缩文件复制到电脑上的适当位置。
温馨提示：确保备份是新的，以避免恢复过时的文件版本。如果备份不完整或损坏，可能无法成功恢复文件。
方法3：显示隐藏恢复
有时长城电脑压缩文件丢失可能被病毒设置为隐藏状态，导致用户无法直接看到。通过显示隐藏文件，用户可以尝试找回这些被隐藏的文件。
1、打开文件资源管理器，点击“查看”选项卡，勾选“隐藏的项目”选项。
2、进入丢失压缩文件所在磁盘，看看文件是否隐藏在某个文件夹或子文件夹中。
温馨提示：如果文件不是被隐藏而是被病毒删除了，那么此方法无效。
方法4：数据恢复软件恢复
若长城电脑上的压缩文件至关重要，建议用户谨慎行事，避免过多操作导致数据被覆盖而无法恢复。
当压缩文件不慎丢失时，建议第一时间使用专业的数据恢复软件，如云骑士数据恢复将大大增加成功恢复数据的几率。这款软件不仅支持免费扫描和预览，而且支持恢复未被覆盖的压缩文件、视频、图片等不同类型文件。
1、启动常备在电脑上的数据恢复软件，针对压缩文件丢失的情境选择相应恢复模式。该软件能有效恢复因误删、格式化或回收站清空等原因造成的数据丢失。
2、接着选择压缩文件原本所在磁盘，如果不确定文件所在位置，可依次勾选扫描排查，勾选后根据软件提示选择”开始扫描“。
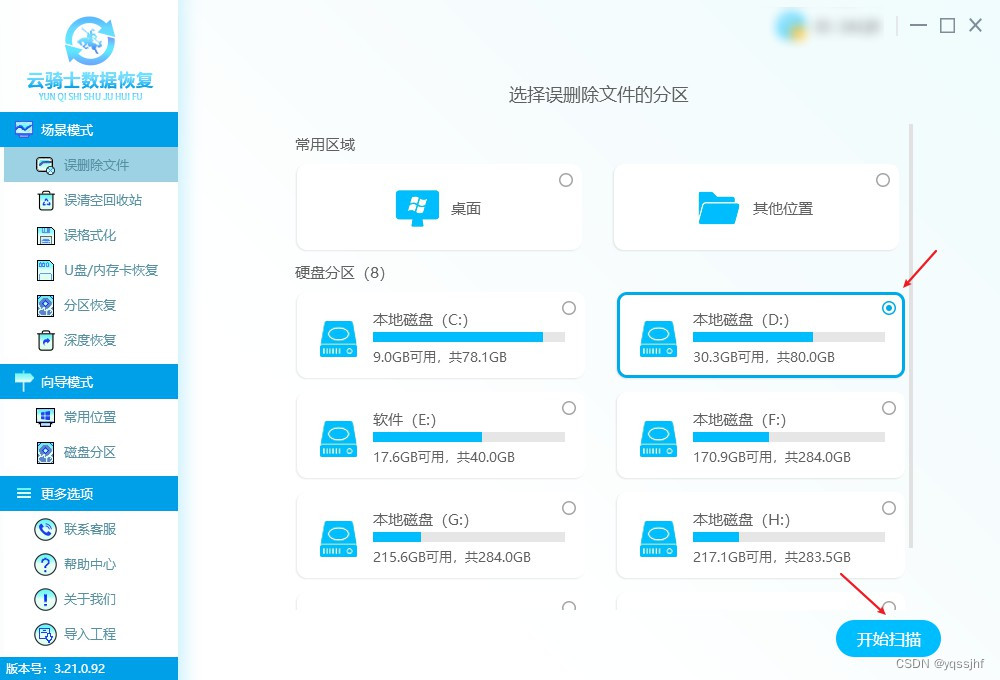
3、完成扫描后，用户可以根据【列表模式】和【预览模式】对扫描结果进行查看，如果对于扫描结果不满意，还可使用“深度扫描”以检索更多数据。
以下是列表模式下快速查找压缩文件有效建议：
若您了解丢失压缩文件的格式，如zip、7z、rar，您可以尝试双击类型下的压缩文件，从而浏览和查找相应格式的文件。
如果知晓丢失压缩文件的名称，可尝试在搜索框中输入该文件名，点击旁边的搜索图标进行快速查找。
如果您知道原本压缩文件的存放路径，如在D:\Windows，可通过原路径方式查找（特别适用于查找文件夹数据）。
4、最后将确认无误的数据勾选上，点击“立即恢复”，在弹出的窗口中选择安全的存储位置，点击“确定”即可将文件进行导出了。
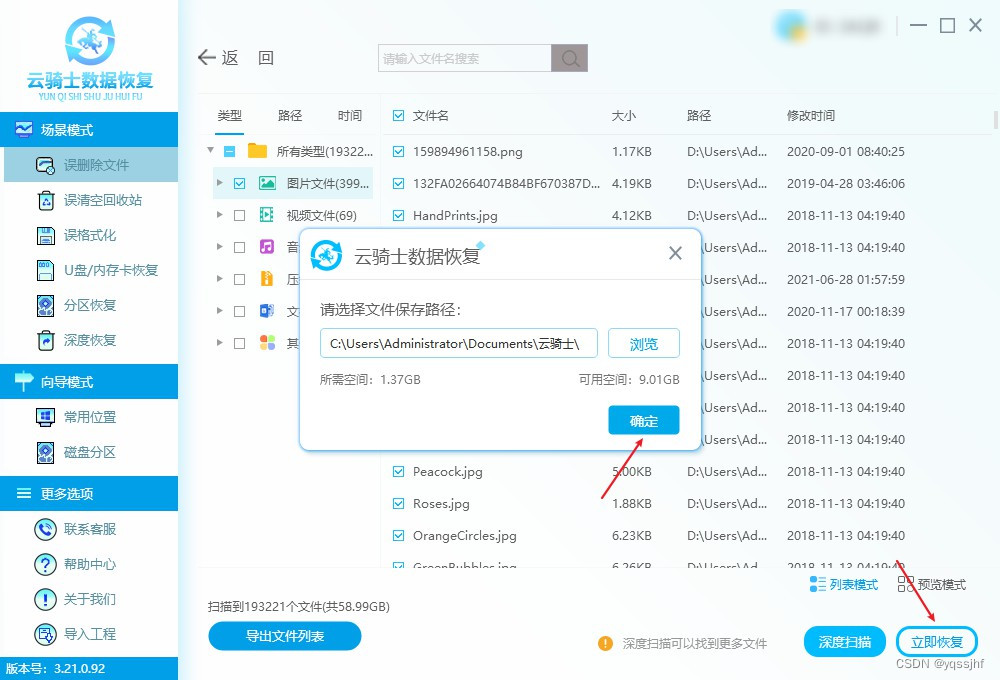
温馨提示：在使用未成功恢复文件之前，尽量不要对丢失文件的磁盘进行写操作，以免覆盖能恢复的文件。
方法5：寻求线下人员恢复
如果您自行无法解决压缩文件丢失的问题，如长城电脑压缩文件丢失是由于硬盘故障导致，建议寻求线下专业技术人员的帮助，以获取更专业的解决方案。
温馨提示：尽量选择有良好声誉和丰富经验的数据恢复服务提供商，而寻求专业帮助可能需要一定的费用和时间成本，应提前做好准备。
三、预防长城电脑压缩文件丢失的措施
- 定期备份：定期备份重要文件，以防万一。
- 谨慎操作：在整理文件时，务必谨慎操作，避免误删除重要文件。
- 安装杀毒软件：安装可靠的杀毒软件，并定期更新病毒库，以防范病毒攻击。
- 维护硬盘健康：定期检查硬盘健康状况，及时修复潜在问题。
结尾：
面对长城电脑压缩文件丢失的问题，我们首先要冷静分析可能的原因，然后采取合适的解决方案。通过本文的介绍，相信读者已经对这一问题有了更为深入的了解。同时，我们也应该认识到预防胜于治疗的重要性，通过定期备份、谨慎操作、安装杀毒软件以及维护硬盘健康等措施，降低压缩文件丢失的风险。
热门推荐：
移动硬盘不小心制作成启动盘怎么办？别慌，这样解决更轻松
电脑怎么使用数据恢复软件：步骤详解与实用指南
笔记本硬盘里的数据怎么拷贝出来
相关文章：
长城电脑压缩文件丢失了怎么办？怎么解决
在数字化时代，电脑已成为我们日常生活和工作中不可或缺的设备。长城电脑作为国内知名品牌，以其稳定可靠的性能赢得了广大用户的信赖。然而，即便是可靠的电脑，也难免会遇到一些问题。其中，压缩文件丢失无疑是一个令人头…...
论文笔记《基于深度学习模型的药物-靶标结合亲和力预测》
基于深度学习模型的药物-靶标结合亲和力预测 这是一篇二区的文章，算是一个综述，记录一下在阅读过程中遇到的问题。 文章目录 基于深度学习模型的药物-靶标结合亲和力预测前言一、蛋白质接触图谱二、为什么蛋白质图谱的准确性对DTA模型预测结果没有影响1…...
ArrayList和LinkedList对比，ArrayList使用注意事项
ArrayList和LinkedList对比，ArrayList使用注意事项 ArrayList 和 LinkedList 是 Java 中常用的两种集合类，它们在内部实现和性能上有一些重要的区别。 ArrayList: ArrayList 是基于动态数组实现的。它内部使用一个数组来存储元素，当数组空间…...
小熊家务帮day5-day7 客户管理模块1 （小程序认证，手机验证码认证,账号密码认证，修改密码，找回密码等）
客户管理模块 1.认证模块1.1 认证方式介绍1.1.1 小程序认证1.1.2 手机验证码登录1.1.3 账号密码认证 1.2 小程序认证1.2.1 小程序申请1.2.2 创建客户后端工程jzo2o-customer1.2.3 开发部署前端1.2.4 小程序认证流程1.2.4.1 customer小程序认证接口设计Controller层Service层调用…...
计算机图形学入门02：线性代数基础
1.向量（Vetors） 向量表示一个方向，还能表示长度（向量的摸）。一般使用单位向量表示方向。 向量加减：平行四边形法则、三角形法则。比卡尔坐标系描述向量，坐标直接相加。 1.1向量点乘（…...
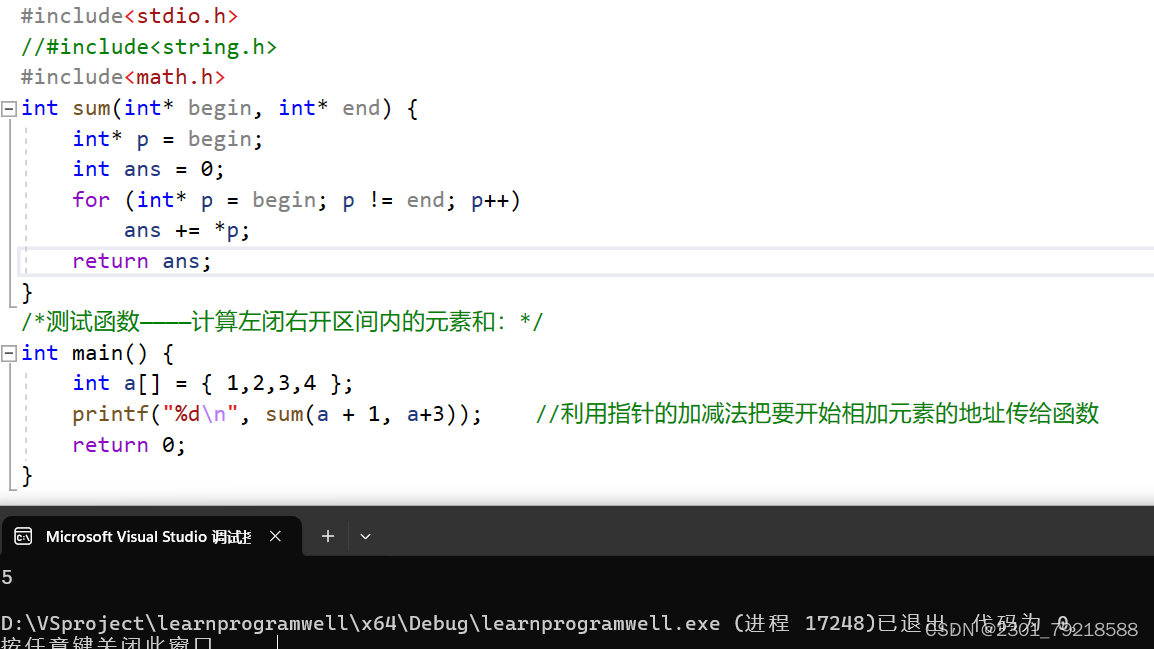
函数：计算数组的元素和
一、计算数组的元素和 参数传递给函数时，实际上只有数组的首地址作为指针传递给了函数。 在函数定义中的int a[ ]等价于int *a。在只有地址信息的情况下，是无法知道数组里有多少个元素的，因此在计算数组中的元素和时，要加一个参…...
如何进行数据库分库分表
当数据库的数据量增长到一定程度，单一数据库或表可能会遇到性能瓶颈，此时分库分表是一种常见的解决方案。以下是如何进行数据库分库分表的详细步骤和考虑因素，结合了参考文章中的相关信息： 一、分库分表概述 分库分表是为了解决…...
Spring-Cloud-CircuitBreaker-Resilience4j （3.1.1）
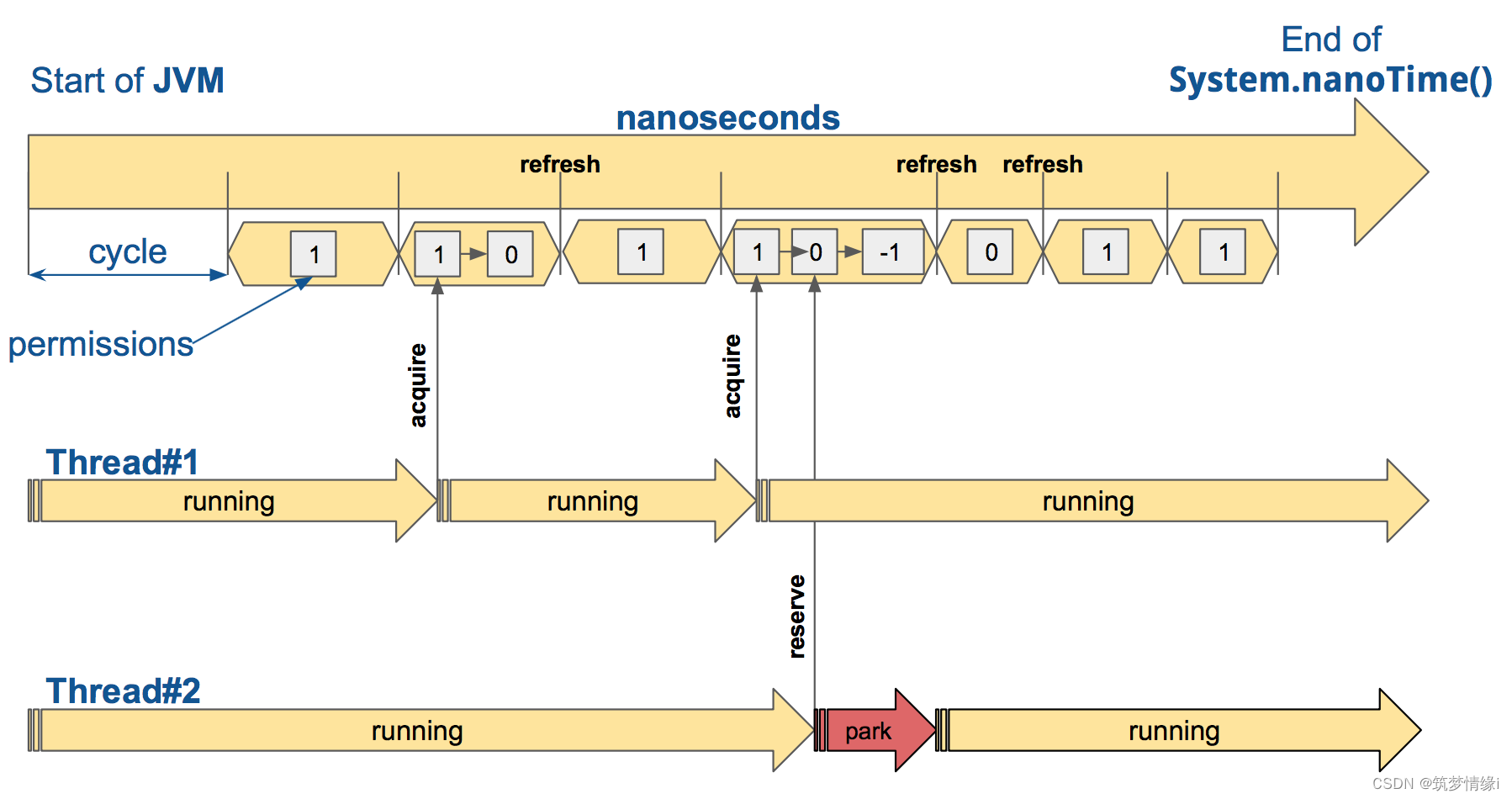
介绍 Resilience4j 是一个专为函数式编程而设计的轻量级容错库。Resilience4j 提供高阶函数（装饰器），以增强任何功能接口、lambda 表达式或方法引用，包括断路器、速率限制器、重试或隔板。您可以在任何函数接口、lambda 表达式或…...
重构与优化-组织数据（3）
重构组织数据是一个系统性的工程，旨在改进数据的存储方式、访问效率、质量和可用性，以更好地支持业务运营、分析决策和未来发展。以下是重构组织数据的一些关键说明点： 目的与动机 提升效率：通过优化数据结构、减少冗余数据和改善索引策略，加快数据查询和处理速度。 增强…...
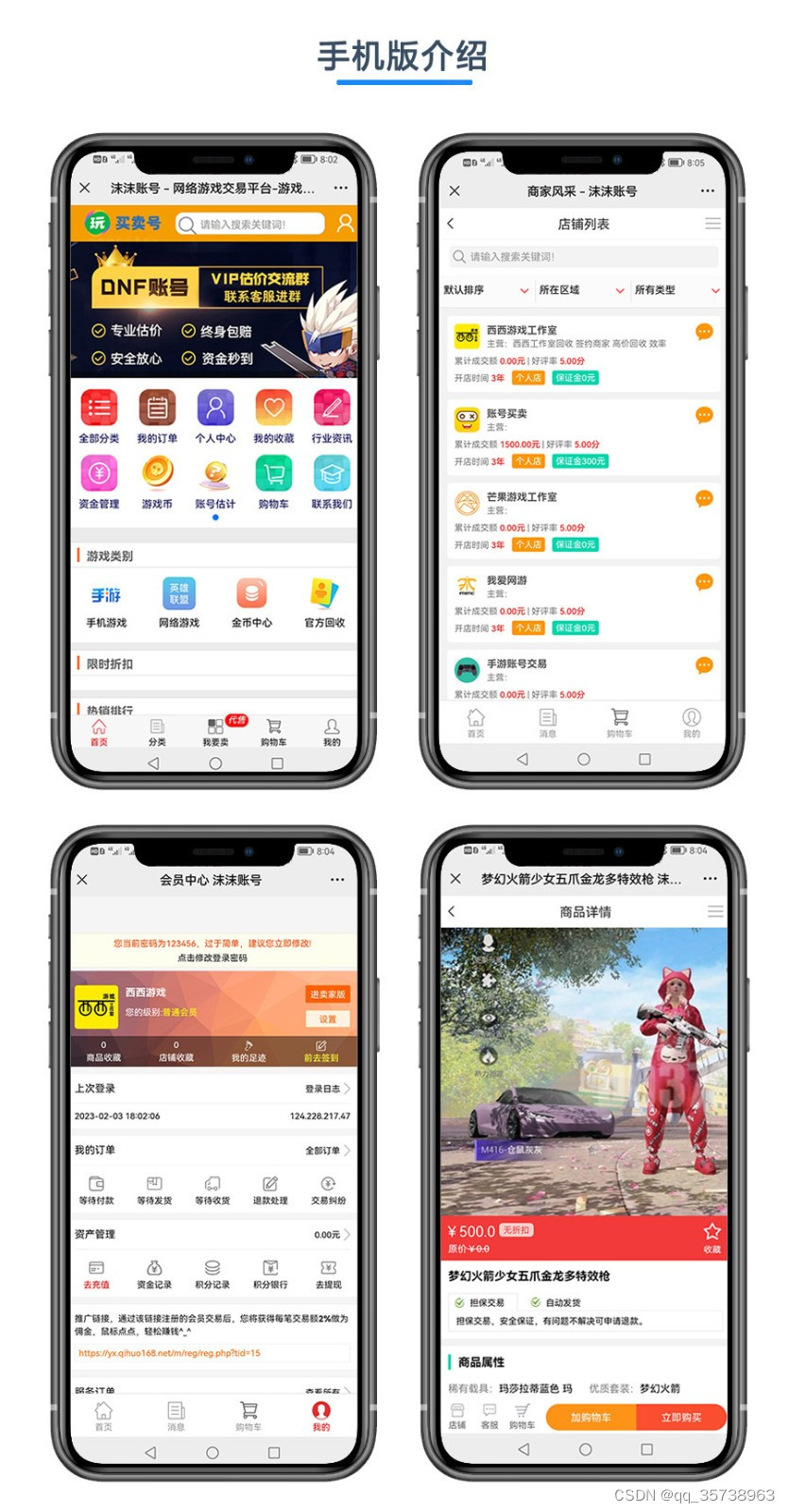
游戏交易平台源码游戏帐号交易平台系统源码
功能介绍 1：后台可以添加删除游戏分类 2：会员中心可以出售游戏币,账号，装备 3：后台可以对会员和商品进行管理 4：多商家入驻,商家发布信息 5：手机版功能可以生成APP 6：在线支付可支持微信和支…...
Matlab里面的浮点数与FPGA定点数的相互转化应用(含Matlab代码，封装成函数可直接调用)
微信公众号获取更多FPGA相关源码： 1.前言 Matlab里面计算通常用的是浮点数，而FPGA在做数字信号处理时，为了节约资源，常常使用的是定点数。在实践中，我们经常需要将Matlab实现中的算法，用FPGA进行实现。 …...
机器学习笔记——欠拟合、过拟合
欠拟合 将训练损失和测试损失都比较大的拟合叫欠拟合，那么他的预测精度很低 1.一般出现在模型的复杂度小于数据本身的复杂度导致的，这个可能就是模型对数据的分布和实际数据分布之间的差异，这个就可能需要更换模型 2.还可能出现在梯度下降算…...
【二进制部署k8s-1.29.4】七、验证master的安装
文章目录 简介 一.确认kubectl命令是否正常运行二.确认etcd安装是否正常运行三.确认kube-apiserver,kube-controller-manager,kube-scheduler安装是否正常四.配置apiserver和kubelet的访问授权五.master端安装脚本4.1.安装master端所需文件4.2.master快捷安装脚本 简介 本章节主…...
springboot获取当前数据库连接
要获取当前 Spring DataSource 的 URL，可以通过以下几种方法： 方法一：使用 JdbcTemplate 如果你使用的是 Spring 的 JdbcTemplate，可以通过 javax.sql.DataSource 获取连接，再获取它的 URL。 示例代码： …...
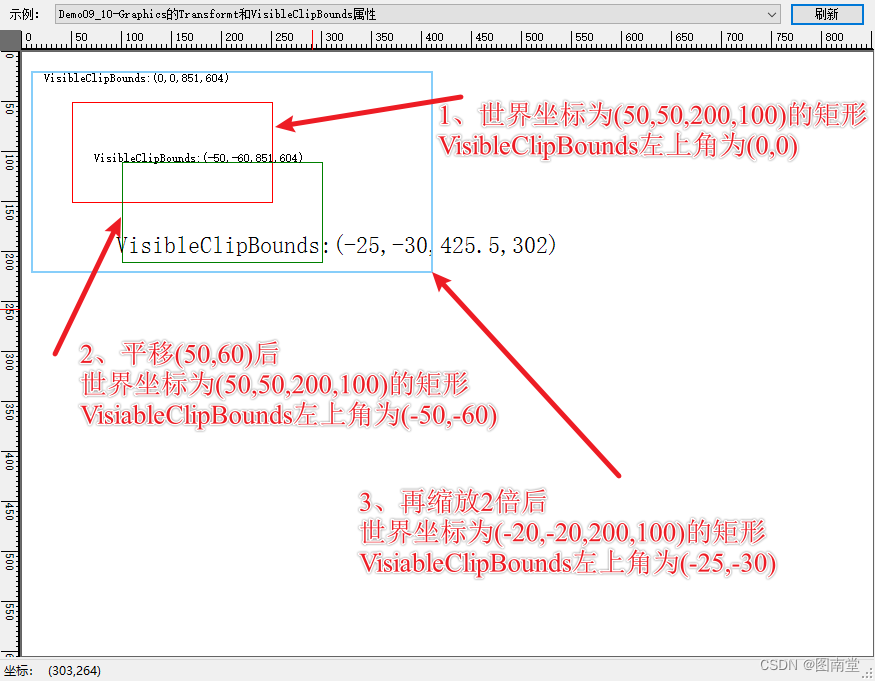
【学习笔记】Windows GDI绘图(九)Graphics详解(上)
文章目录 Graphics 定义创建Graphics对象的方法通过Graphics绘制不同的形状、线条、图像和文字等通过Graphics操作对象坐标 Graphics属性Clip(裁切/绘制区域)ClipBounds获取裁切区域矩形范围CompositiongMode合成方式CompositingQuality渲染质量DpiX和DpiY 水平、垂直分辨率Int…...
公告：公众号铁粉粉丝介绍以及说明
大家好，我是公众号博主--夏目 机械电气电机杂谈是我个人建立，为分享机械，电气，电机知识为主，闲谈杂聊社会时事，职场见闻，生活琐事，成长趣事，学习心得，读书观影…...
BioTech - 使用 CombFold 算法 实现 大型蛋白质复合物结构 的组装过程
欢迎关注我的CSDN：https://spike.blog.csdn.net/ 本文地址：https://spike.blog.csdn.net/article/details/139242199 CombFold 是用于预测大型蛋白质复合物结构的组合和分层组装算法，利用 AlphaFold2 预测的亚基之间的成对相互作用。 CombFold 算法的关键特点包括： 组合和…...
代码随想录算法训练营第36期DAY46
DAY46 完全背包 在闫氏DP法里学过：第i个物品选k个，纸质直至不能选，k从0开始取。就有递推式了。 代码随想录的视频也看了。 518零钱兑换ii 注意与 目标和 那题区分开。 完全背包问题，正向遍历背包容量，就能实现“多次…...
港湾周评|李小加“刀刃向内”裁员
《港湾商业观察》李镭 近年来争议颇大的滴灌通风波不断。 在交100万付费上班不久，最新又被曝出裁员。这位前港交所总裁、金融圈鼎鼎大名的李小加，没想到成立不足三年便迎来了重大挑战。 日前，滴灌通确认了公司组织架构已经调整，…...
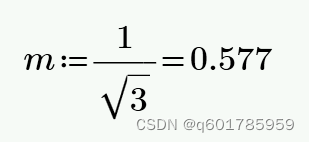
超大功率光伏并网逆变器学习(三相)
1.超大功率用的IGBT开关频率通常很低,比如6KHz 2.线电压和相电压的关系 相电压 A AB线电压-CA线电压 相电压 B BC线电压-AB线电压 相电压 C CA线电压-BC线电压 3.坐标变换 ABC三相信号通过Clark坐标变换得到αβ两相静止信号,其中α与A相重合,β与α…...
web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段： 构建阶段（Build Stage）：…...
系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log，共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题，不能使用ELK只能使用…...
生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端（Windows 使用 Git Bash，Mac/Linux 使用 Terminal）执行命令： ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明： -t rsa&#x…...
Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ；并安装。 基础操作不再赘述。 打开 macOS 终端，开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
推荐 github 项目:GeminiImageApp(图片生成方向，可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向，可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项： 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库： npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
 Module Federation：Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation：Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例，Webpack.config.js它可能的配置和含义如下： 前言 Module Federation 的Webpack.config.js核心配置包括： name filename（定义应用标识） remotes（引用远程模块࿰…...
【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明，此教程是针对Simulink编译模型并导入Veristand中编写的，同时需要注意的是老用户编译可能用的是Veristand Model Framework，那个是历史版本，且NI不会再维护，新版本编译支持为VeriStand Model Generation Suppo…...
DiscuzX3.5发帖json api
参考文章：PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下，适配我自己的需求 有一个站点存在多个采集站，我想通过主站拿标题，采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
加密通信 + 行为分析：运营商行业安全防御体系重构
在数字经济蓬勃发展的时代，运营商作为信息通信网络的核心枢纽，承载着海量用户数据与关键业务传输，其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级，传统安全防护体系逐渐暴露出局限性&a…...