计算机图形学入门02:线性代数基础
1.向量(Vetors)
向量表示一个方向,还能表示长度(向量的摸)。一般使用单位向量表示方向。
向量加减:平行四边形法则、三角形法则。比卡尔坐标系描述向量,坐标直接相加。
1.1向量点乘(Dot product)
向量点乘也可以交向量点积,向量的数量积公式:a*b=|a||b|cosθ a,b表示向量,θ表示向量a,b共起点时的夹角,很明显向量的数量积表示数,不是向量。
性质:

在笛卡尔坐标下:
二维向量点乘
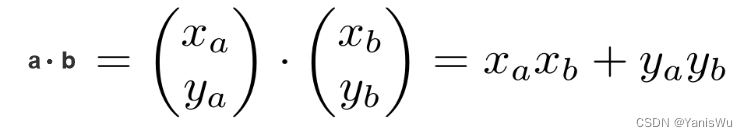
三位向量点乘
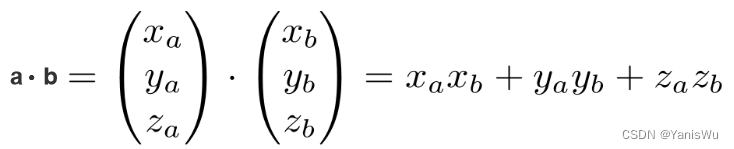
向量点乘的作用:
1.能够快速获得两个方向的夹角(例如光源与表面夹角的余弦),通过夹角也可判断两个向量的接近程度。
2.求一个向量在另一个向量的投影。

投影在图形学中的好处:
1.测量两个方向的距离
2.分解一个向量
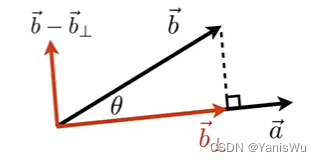
3.确定向前/向后
如果结果是0到1,那么方向相同,如果是-1到0则方向相反,如果等于0则垂直。
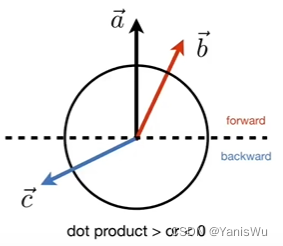
1.2向量叉乘(Cross product)
向量叉乘又称向量积,与点积不同,它的运算结果是一个向量而不是一个标量。
叉乘的属性:
1.向量积与两个初始向量正交。垂直。
2.通过右手法则求得。可得不满足交换率,如果要使用交换律,其中一个向量要加一个负号。
3.建立三维空间直角坐标系。知道两个x,y轴,就可以算出z轴。如果x叉乘y等于z,那么就可以判定坐标系为右手坐标系。OpenGL使用右手坐标系,DirectX使用左手坐标系。
叉乘的运算:
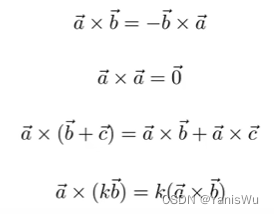
在笛卡尔坐标系下:
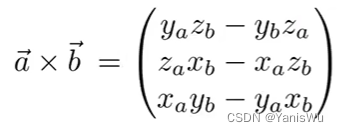
用矩阵表示(后面会讲):
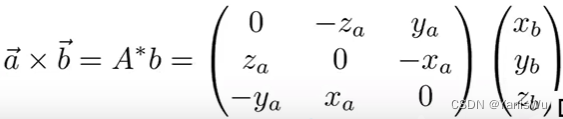
叉乘的作用:
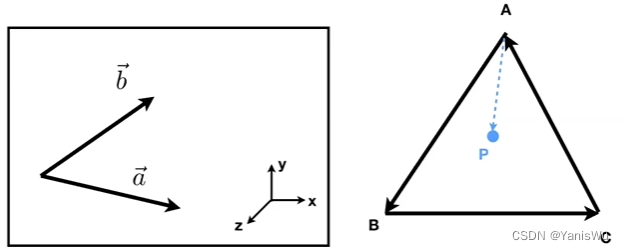
1.判定左右。a向量叉乘b,使用右手螺旋定则,如果大拇指向上且四指方向从a转向b,则b在a的左边。
2.判定内外。如下图A-B-C,依次做运算,AB向量叉乘AP,BC向量叉乘BP,CA向量叉乘CP,发现AP,BP,CP,分别在AB,BC,CA的左边,即可以判定,P点在三角形的内部;如果以A-C-B方向,都在其右边,同样可以判定在三角形内部。即不论顺序,P点的三个结果都是同一侧,则P点在三角形的内部。在图形学的光珊化阶段,用来判断像素点是否在三角形内部,从而给像素颜色。
1.3标准正交坐标系
定义三个单位向量u、v、w,并且都互相垂直,也就是点乘结果都为0,给u和v叉乘结果为w,对应x与y叉乘等于z,得到一个右手的三维直角坐标系。
好处是可以把任意向量都分解到三个轴去,通过投影计算。由于都是单位向量,所以p分解到三个轴上后,p向量投影到u向量的点乘乘以u方向,同理获取v上的投影方向和w上的投影方向,并且三个投影方向加起来等于p原向量。
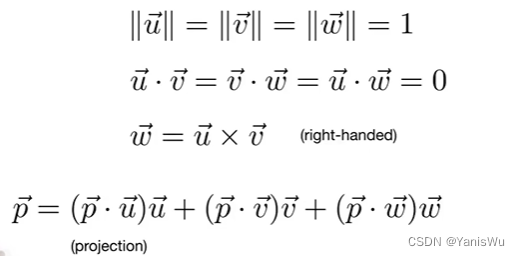
2.矩阵(Matrices)
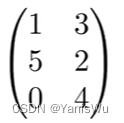
矩阵是一个数学概念,它是由一组数排成的矩形阵列,通常用方括号或圆括号来表示。数字数组(m行,n列),如下图所示为一个3行2列的矩阵。
2.1矩阵乘积
矩阵与一个常数相乘比较简单,直接矩阵里每个元素分别乘以这个常数。这里直接了解矩阵与矩阵相乘。
矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义。例如第一个为m行n列的矩阵,第二个矩阵是n行p列的矩阵,那么相乘的结果是一个m行p列的矩阵。
设A为![]() 的矩阵,B为
的矩阵,B为![]() 的矩阵,那么称
的矩阵,那么称![]() 的矩阵C为矩阵A与B的乘积,记作
的矩阵C为矩阵A与B的乘积,记作![]() ,其中矩阵C中的第i行第j列元素可以表示为:
,其中矩阵C中的第i行第j列元素可以表示为:
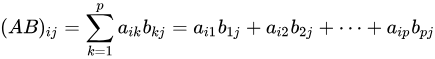
如下图所示:

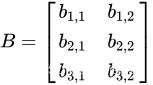
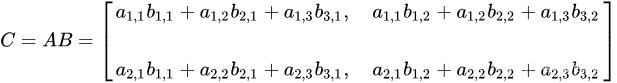
基本性质:
1.满足结合法和分配法:
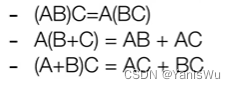
2.不满足交换律,即AB!=BA
2.2矩阵与向量乘
可将向量视为列矩阵(m x 1),列数为1。这是变换点的关键,例如将(x,y)向量变换为(-x,y)的向量,做镜像处理。可以如下操作。
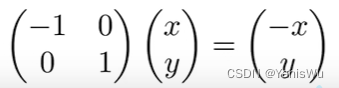
2.3矩阵的加减运算
矩阵加减运算,涉及将两个矩阵中对应位置的元素进行加法或减法操作。这种运算的前提是参与运算的两个矩阵必须具有相同的行数和列数,即它们是同型矩阵。矩阵的加法运算可以简单地理解为将两个矩阵中对应位置的元素相加,而减法运算则是对应位置的元素相减。例如,如果矩阵A=[1 2]和B=[2 3],那么A+B=[1+2 2+3]=[3 5]。
2.4矩阵的转置
将矩阵的行列互换得到的新矩阵称为转置矩阵,转置矩阵的行列式不变。
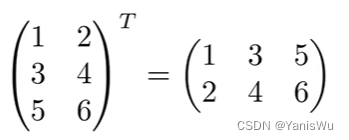
性质:
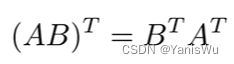
2.5单位矩阵和逆矩阵
单位矩阵:
在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵。它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0。
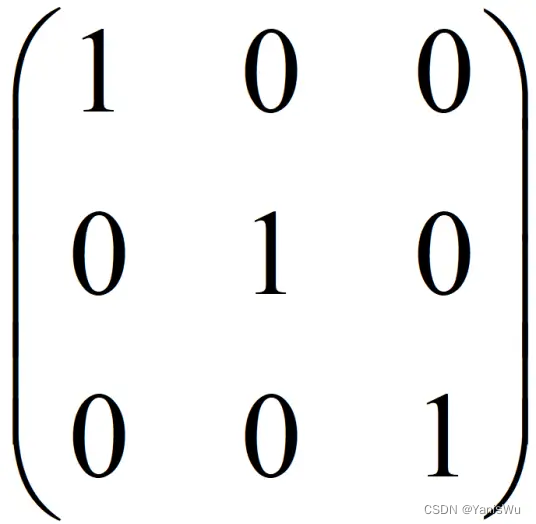
根据单位矩阵的特点,任何矩阵与单位矩阵相乘都等于本身。
逆矩阵:
如果第一个矩阵乘以第二个矩阵的结果为一个单位矩阵,那么另外一个矩阵就是第一个矩阵的逆矩阵。也就是说一个A矩阵乘以它的逆矩阵就能求出单位矩阵I。

逆矩阵的一个性质与转置的性质比较像,如下:

2.6矩阵形式的向量乘法
向量的点乘表示:
前面说过可以将向量视为一个列数的矩阵,那么两个向量的点乘可视为两个矩阵的相乘,又因为矩阵的相乘特性,所以必须将一个向量变成转置。如下:
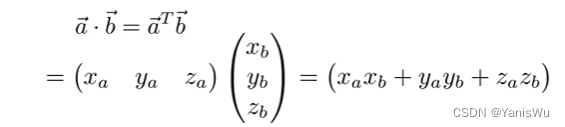
向量的叉乘表示:
向量的叉乘可以写成一个向量对应的矩阵乘以另一个向量。
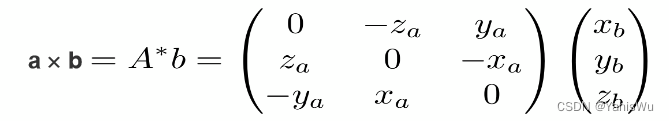
通过矩阵乘法规则推理得出下面结果。

相关文章:

计算机图形学入门02:线性代数基础
1.向量(Vetors) 向量表示一个方向,还能表示长度(向量的摸)。一般使用单位向量表示方向。 向量加减:平行四边形法则、三角形法则。比卡尔坐标系描述向量,坐标直接相加。 1.1向量点乘(…...
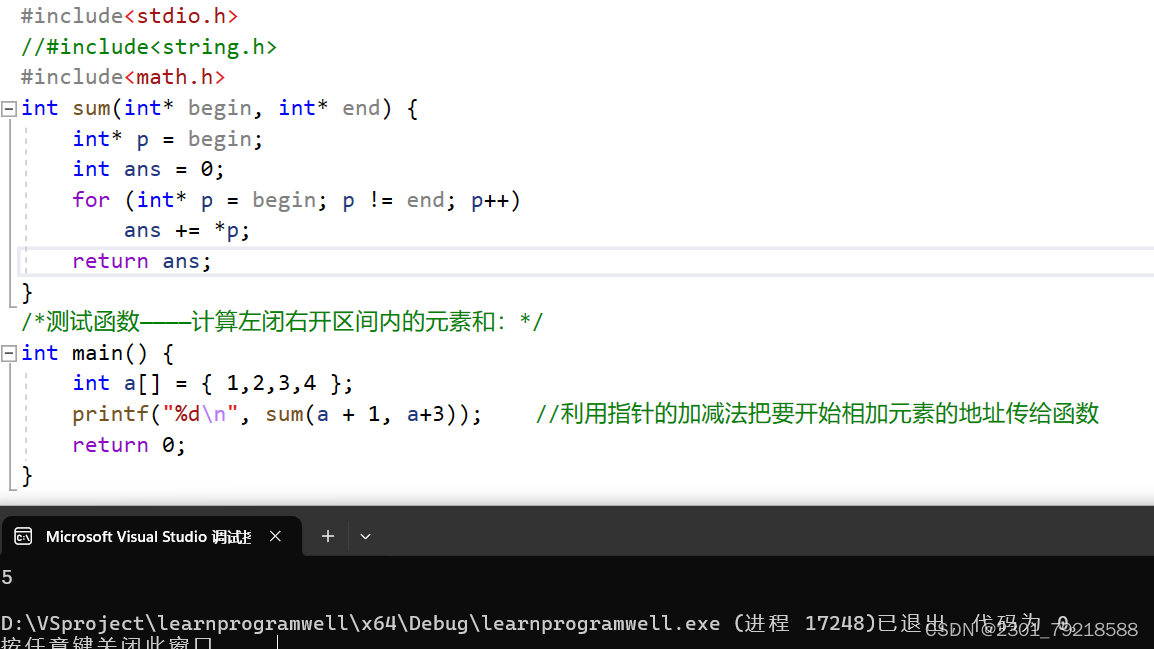
函数:计算数组的元素和
一、计算数组的元素和 参数传递给函数时,实际上只有数组的首地址作为指针传递给了函数。 在函数定义中的int a[ ]等价于int *a。在只有地址信息的情况下,是无法知道数组里有多少个元素的,因此在计算数组中的元素和时,要加一个参…...

如何进行数据库分库分表
当数据库的数据量增长到一定程度,单一数据库或表可能会遇到性能瓶颈,此时分库分表是一种常见的解决方案。以下是如何进行数据库分库分表的详细步骤和考虑因素,结合了参考文章中的相关信息: 一、分库分表概述 分库分表是为了解决…...
Spring-Cloud-CircuitBreaker-Resilience4j (3.1.1)
介绍 Resilience4j 是一个专为函数式编程而设计的轻量级容错库。Resilience4j 提供高阶函数(装饰器),以增强任何功能接口、lambda 表达式或方法引用,包括断路器、速率限制器、重试或隔板。您可以在任何函数接口、lambda 表达式或…...
)
重构与优化-组织数据(3)
重构组织数据是一个系统性的工程,旨在改进数据的存储方式、访问效率、质量和可用性,以更好地支持业务运营、分析决策和未来发展。以下是重构组织数据的一些关键说明点: 目的与动机 提升效率:通过优化数据结构、减少冗余数据和改善索引策略,加快数据查询和处理速度。 增强…...
游戏交易平台源码游戏帐号交易平台系统源码
功能介绍 1:后台可以添加删除游戏分类 2:会员中心可以出售游戏币,账号,装备 3:后台可以对会员和商品进行管理 4:多商家入驻,商家发布信息 5:手机版功能可以生成APP 6:在线支付可支持微信和支…...

Matlab里面的浮点数与FPGA定点数的相互转化应用(含Matlab代码,封装成函数可直接调用)
微信公众号获取更多FPGA相关源码: 1.前言 Matlab里面计算通常用的是浮点数,而FPGA在做数字信号处理时,为了节约资源,常常使用的是定点数。在实践中,我们经常需要将Matlab实现中的算法,用FPGA进行实现。 …...

机器学习笔记——欠拟合、过拟合
欠拟合 将训练损失和测试损失都比较大的拟合叫欠拟合,那么他的预测精度很低 1.一般出现在模型的复杂度小于数据本身的复杂度导致的,这个可能就是模型对数据的分布和实际数据分布之间的差异,这个就可能需要更换模型 2.还可能出现在梯度下降算…...

【二进制部署k8s-1.29.4】七、验证master的安装
文章目录 简介 一.确认kubectl命令是否正常运行二.确认etcd安装是否正常运行三.确认kube-apiserver,kube-controller-manager,kube-scheduler安装是否正常四.配置apiserver和kubelet的访问授权五.master端安装脚本4.1.安装master端所需文件4.2.master快捷安装脚本 简介 本章节主…...

springboot获取当前数据库连接
要获取当前 Spring DataSource 的 URL,可以通过以下几种方法: 方法一:使用 JdbcTemplate 如果你使用的是 Spring 的 JdbcTemplate,可以通过 javax.sql.DataSource 获取连接,再获取它的 URL。 示例代码: …...
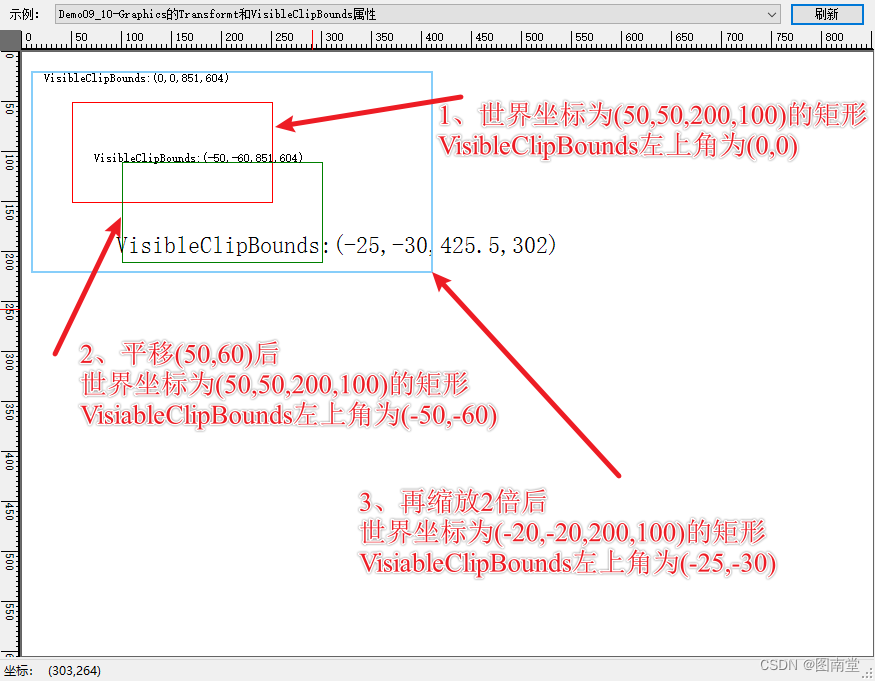
【学习笔记】Windows GDI绘图(九)Graphics详解(上)
文章目录 Graphics 定义创建Graphics对象的方法通过Graphics绘制不同的形状、线条、图像和文字等通过Graphics操作对象坐标 Graphics属性Clip(裁切/绘制区域)ClipBounds获取裁切区域矩形范围CompositiongMode合成方式CompositingQuality渲染质量DpiX和DpiY 水平、垂直分辨率Int…...

公告:公众号铁粉粉丝介绍以及说明
大家好,我是公众号博主--夏目 机械电气电机杂谈是我个人建立,为分享机械,电气,电机知识为主,闲谈杂聊社会时事,职场见闻,生活琐事,成长趣事,学习心得,读书观影…...

BioTech - 使用 CombFold 算法 实现 大型蛋白质复合物结构 的组装过程
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/139242199 CombFold 是用于预测大型蛋白质复合物结构的组合和分层组装算法,利用 AlphaFold2 预测的亚基之间的成对相互作用。 CombFold 算法的关键特点包括: 组合和…...

代码随想录算法训练营第36期DAY46
DAY46 完全背包 在闫氏DP法里学过:第i个物品选k个,纸质直至不能选,k从0开始取。就有递推式了。 代码随想录的视频也看了。 518零钱兑换ii 注意与 目标和 那题区分开。 完全背包问题,正向遍历背包容量,就能实现“多次…...

港湾周评|李小加“刀刃向内”裁员
《港湾商业观察》李镭 近年来争议颇大的滴灌通风波不断。 在交100万付费上班不久,最新又被曝出裁员。这位前港交所总裁、金融圈鼎鼎大名的李小加,没想到成立不足三年便迎来了重大挑战。 日前,滴灌通确认了公司组织架构已经调整,…...
超大功率光伏并网逆变器学习(三相)
1.超大功率用的IGBT开关频率通常很低,比如6KHz 2.线电压和相电压的关系 相电压 A AB线电压-CA线电压 相电压 B BC线电压-AB线电压 相电压 C CA线电压-BC线电压 3.坐标变换 ABC三相信号通过Clark坐标变换得到αβ两相静止信号,其中α与A相重合,β与α…...

大豆、棉花深度学习数据集大合集
最近收集了一大波关于大豆和棉花的深度学习数据集,主要有叶片的识别、分类、计数以及病害检测等。 数据集的价值 科研价值:这些数据集为植物学、农业信息技术、机器学习等领域的科研人员提供了宝贵的资源。它们可以用于训练和优化各种深度学习模型&…...

教育数字展馆助力全球教育传播,科技引领数字化教育潮流
一、教育数字展馆助力教育传播 1、提高教育资源的可及性 教育数字展馆通过VR和WEB3D技术,将丰富的教育资源呈现在用户面前。不论是名校的经典课程,还是专家的精彩讲座,均可通过教育数字展馆实现线上展示。用户只需登录平台,即可…...
14.微信小程序之地理定位功能
目录 1.地理定位介绍 1.1 申请开通 1.2 使用方法 2.拒绝授权后的解决方案 3.开通腾讯位置服务 4.LBS 逆地址解析 1.地理定位介绍 小程序地理定位是指通过小程序开发平台提供的 API,来获取用户的地理位置信息。用户在使用小程序时,可以授权小程序获…...

理解lambda表达式
Lambda表达式: 这里不再过多叙述什么事lambda表达式,就说下怎么使用,首先和lambda表达式同时存在的就是另一个定义,就是匿名内部类。匿名内部类首先需要一个接口。 下面用一个例子说明lambda表达式: public class Hel…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
