代码随想录算法训练营Day24|216.组合总和III、17.电话号码的字母组合
组合总和III
216. 组合总和 III - 力扣(LeetCode)
思路和昨日的组合题类似,但注意对回溯算法中,收获时的条件需要写对,path的长度要为k的同时,path中元素总和要为n。
class Solution {
public:vector<int> path;vector<vector<int>> paths;int sum = 0; // 维护当前路径的和void backtracking(int k, int n, int startindex) {if (path.size() == k && sum == n) {paths.push_back(path);return;}for (int i = startindex; i <= 9; i++) {path.push_back(i);sum += i; // 更新路径和backtracking(k, n, i + 1);sum -= i; // 回溯时,恢复路径和path.pop_back();}}vector<vector<int>> combinationSum3(int k, int n) {backtracking(k, n, 1);return paths;}
};
算法的时间复杂度,在最差的情况需,我们需要生成所有C(9,n)个组合,并且对于每个组合,都需要进行k层递归,因此时间复杂度为O(C(9,n)*n)。
空间复杂度考虑递归栈,递归栈的最大深度为n,每个组合需要n个元素的存储空间,隐形空间复杂度是O(n)。
电话号码的字母组合
17. 电话号码的字母组合 - 力扣(LeetCode)
首先,考虑使用一个哈希表来存储数值(这里用数值方便些,之后用 i - '0'可以将char转换为整形)与字符的映射关系。
具体参考代码随想录 (programmercarl.com)
回溯三步法
1.确定回溯函数参数,我们每次回溯返回的值都会存放在一个path字符串中,并存在一个paths数组存放所有的组合结果中,我们用全局变量表示,此外,我们还需要一个变量index来指示现在遍历的位置。
2.确认终止条件。当index与需要遍历的字符长度相同时,就将值存入path中,并返回。
3.单层遍历逻辑,我们需要知道在当前index下的umap存储的字符串大小,然后对这个字符串中的字符进行递归遍历。之后对下一个字符进行处理,因为本题是求不同集合间的组合。
整体代码
class Solution {
public:vector<string> paths; // 用于存储所有可能的字母组合string path; // 用于存储当前的字母组合unordered_map<int, vector<char>> umap; // 创建一个映射表,将数字映射到对应的字母Solution() {umap[2] = {'a', 'b', 'c'}; // 数字2对应的字母umap[3] = {'d', 'e', 'f'}; // 数字3对应的字母umap[4] = {'g', 'h', 'i'}; // 数字4对应的字母umap[5] = {'j', 'k', 'l'}; // 数字5对应的字母umap[6] = {'m', 'n', 'o'}; // 数字6对应的字母umap[7] = {'p', 'q', 'r', 's'}; // 数字7对应的字母umap[8] = {'t', 'u', 'v'}; // 数字8对应的字母umap[9] = {'w', 'x', 'y', 'z'}; // 数字9对应的字母}void backtracking(const string& digits, int index) {// 如果当前组合的长度等于输入数字的长度,将当前组合添加到结果中if (index == digits.size()) {paths.push_back(path);return;}// 将当前处理的数字转换为对应的映射表中的字母int digit = digits[index] - '0'; // 遍历映射表中的字母,进行回溯for (int i = 0; i < umap[digit].size(); i++) {path.push_back(umap[digit][i]); // 添加字母到当前组合backtracking(digits, index + 1); // 处理下一个数字path.pop_back();}}vector<string> letterCombinations(string digits) {//输入为空,直接返回空的结果if (digits.empty()) {return paths;}backtracking(digits, 0);return paths;}
};
算法的时间复杂度参考在最坏情况下,每个数字对应最多4个字母,若输入数字的长度为n,则最坏情况下时间复杂度为O(4^n),因为每一步都有4种选择。代码随想录上是将3个字母和4个字母都区分了出来所以是O(3^m*4^n)
空间复杂度由两部分组成,一是递归的栈空间,二是存储结果的空间,栈空间最坏情况下与输入数字长度n成正比O(n)。存储空间取决于可能的组合数量,最坏情况下为O(4^n),总的空间复杂度为O(m+4^n)。
相关文章:

代码随想录算法训练营Day24|216.组合总和III、17.电话号码的字母组合
组合总和III 216. 组合总和 III - 力扣(LeetCode) 思路和昨日的组合题类似,但注意对回溯算法中,收获时的条件需要写对,path的长度要为k的同时,path中元素总和要为n。 class Solution { public:vector<…...

【Python系列】Python 中方法定义与方法调用详解
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
)
Java 基础面试300题 (201-230)
Java 基础面试300题 (201-230) 201.下面代码片段的输出是什么? Predicate<Integer> numberChecker (num)–> num > 20; int input 10; System.out.println(input” greater than 20–”numberChecker.test(input)); //Line 1…...

Go-知识并发控制Context
Go-知识并发控制Context 1. 介绍2. 实现原理2.1 接口定义2.2 Deadline()2.3 Done()2.4 Err()2.5 Value() 3. 空 context4. cancelCtx4.1 Done()4.2 Err()4.3 cancel()4.4 WithCancel4.5 例子4.6 总结 5. timerCtx5.1 Deadline5.2 cancel5.3 WithDeadline5.4 WithTimeout5.5 例子…...

Vue + Nodejs + socket.io 实现聊天
Vue 代码 // 安装 socket.io-clientnpm i socket.io-clientimport io from socket.io-client;mounted () {// * location.origin 表示你的 socket 服务地址// * /XXXX/socket.io 表示 你的 socket 在服务器配置的 访问地址let socket io(location.origin, {path: "/XX…...
cocos creator 3.x实现手机虚拟操作杆
简介 在许多移动游戏中,虚拟操纵杆是一个重要的用户界面元素,用于控制角色或物体的移动。本文将介绍如何在Unity中实现虚拟操纵杆,提供了一段用于移动控制的代码。我们将讨论不同类型的虚拟操纵杆,如固定和跟随,以及如…...

【数据分享】中国电力年鉴(2004-2022)
大家好!今天我要向大家介绍一份重要的中国电力统计数据资源——《中国电力年鉴》。这份年鉴涵盖了从2004年到2022年中国电力统计全面数据,并提供限时免费下载。(无需分享朋友圈即可获取) 数据介绍 自1993年首次出版以来…...

两个数组的交集Ⅱ-力扣
想到的解法是使用两个map来进行记录,mp1用来统计num1中每个元素出现的次数。当nums2的元素能够在mp1中查找到时,将这个元素添加到mp2,按照这个规则统计得到nums2和nums1重复的元素,mp2中的value记录了nums2中这个元素出现的次数最…...

【TCP协议中104解析】wireshark抓取流量包工具,群殴协议解析基础
Tcp ,104 ,wireshark工具进行解析 IEC104 是用于监控和诊断工业控制网络的一种标准,而 Wireshark则是一款常用的网络协议分析工具,可以用干解析TEC104 报文。本文将介绍如何使用 Wireshark解析 IEC104报文,以及解析过 程中的注意事项。 一、安…...
[个人笔记] 记录docker-compose使用和Harbor的部署过程
容器技术 第三章 记录docker-compose使用和Harbor的部署过程 容器技术记录docker-compose使用和Harbor的部署过程Harborhttps方式部署:测试环境部署使用自签名SSL证书https方式部署:正式环境部署使用企业颁发的SSL证书给Docker守护进程添加Harbor的SSL证…...
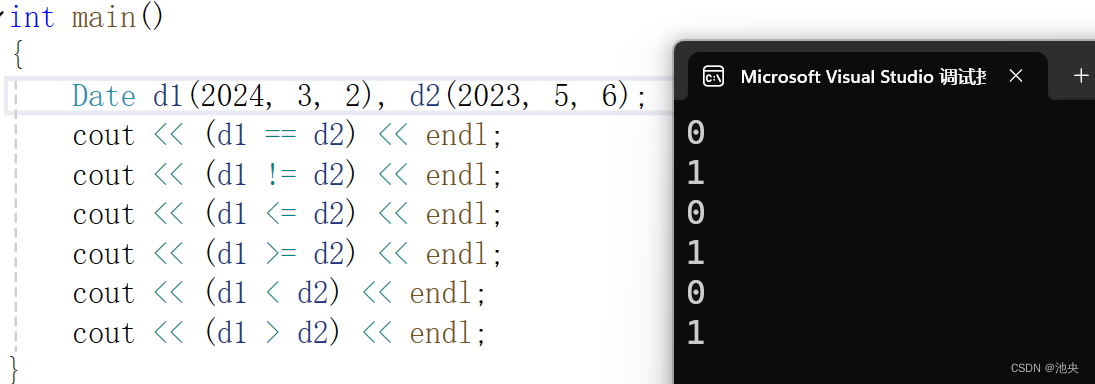
详细介绍运算符重载函数,清晰明了
祝各位六一快乐~ 前言 1.为什么要进行运算符重载? C中预定义的运算符的操作对象只能是基本数据类型。但实际上,对于许多用户自定义类型(例如类),也需要类似的运算操作。这时就必须在C中重新定义这些运算符ÿ…...

国内外知名的低代码开发平台下载地址
以下是国内外几款低代码开发平台的列表,包含了下载地址、适应操作系统、是否可以独立部署、优点、缺点以及是否包含流程引擎的信息。 平台名称 下载地址 适应操作系统 是否可以独立部署 优点 缺点 是否包含流程引擎 国内平台 阿里云宜搭 阿里云官网 跨平台…...
【Pr学习】01新建项目起步
【Pr学习】01新建项目起步 1、新建项目2.序列设置2.1新建序列2.2序列参数讲解2.3自定义设置 3.PR窗口认识3.1 项目窗口3.2 源窗口2.4 保存面板 4.剪辑导入4.1 素材导入4.2 视图切换4.3 时间轴4.4轨道工具4.5 节目窗口素材导入 5.基础操作5.1 取消视频音频链接5.2 单独渲染&…...

【Redis延迟队列】redis中的阻塞队列和延迟队列
阻塞队列(RBlockingQueue) 作用和特点: 实时性:阻塞队列用于实时处理消息。生产者将消息放入队列,消费者可以立即从队列中取出并处理消息。阻塞特性:如果队列为空,消费者在尝试获取消息时会被…...

el-tree常用操作
一、定义 <el-treeclass"myTreeClass":data"dirTreeData":props"dirTreeProps":filter-node-method"filterDirTree":expand-on-click-node"false"node-key"id"node-click"dirTreeNodeClick":allow-…...

SQL 语言:存储过程和触发器
文章目录 基本概述创建触发器更改和删除触发器总结 基本概述 存储过程,类似于高阶语言的函数或者方法,包含SQL语句序列,是可复用的语句,保存在数据库中,在服务器中执行。特点是复用,提高了效率,…...

Ubuntu Linux 24.04 使用certbot生成ssl证书
设置域名 1. 将需要生成SSL证书的域名解析到IP地址 idealand.xyz <> 64.176.82.190 检查防火墙的设置 1. 首先查看防火墙的状态: # ufw status 2. 如果防火墙开启了,要开放80和443端口用于certbot验证 # ufw allow 80 # ufw allow 443 生…...
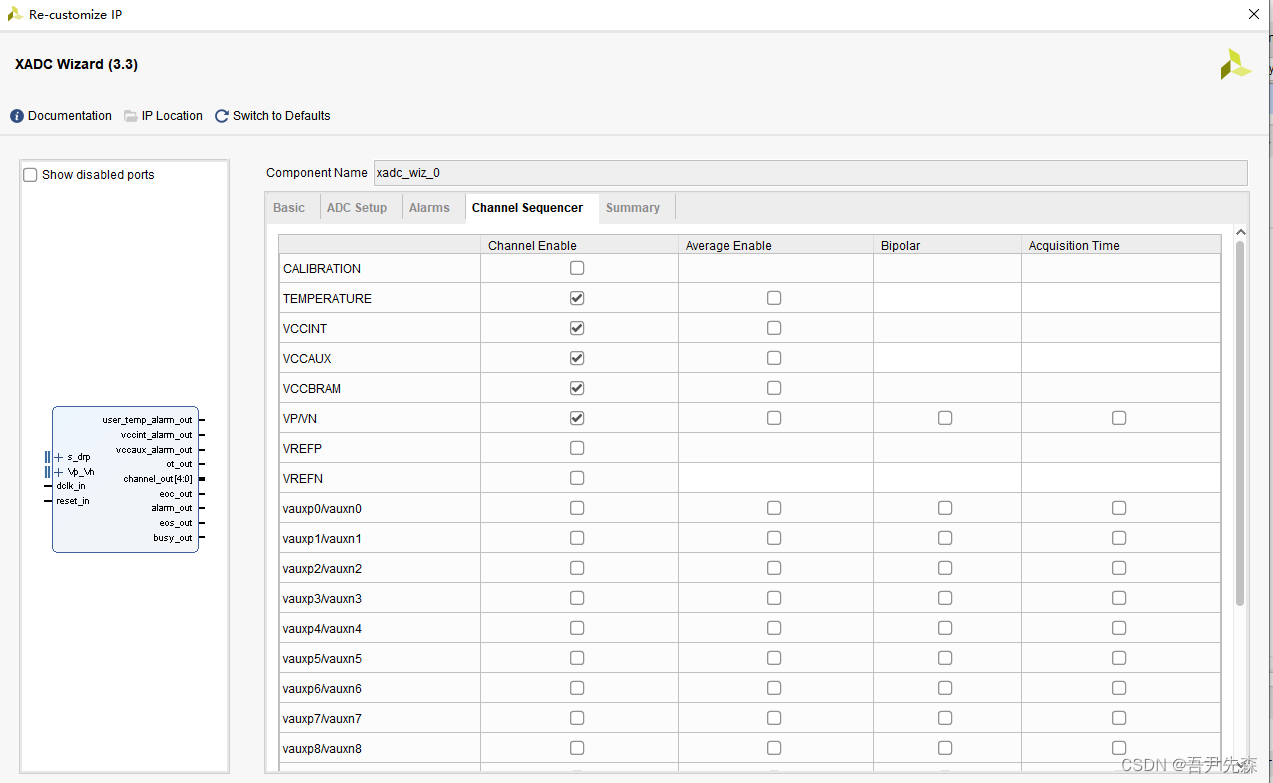
Vivado 比特流编译时间获取以及FPGA电压温度获取(实用)
Vivado 比特流编译时间获取以及FPGA电压温度获取 语言 :Verilg HDL 、VHDL EDA工具:ISE、Vivado Vivado 比特流编译时间获取以及FPGA电压温度获取一、引言二、 获取FPGA 当前程序的编译时间verilog中直接调用下面源语2. FPGA电压温度获取(1&a…...
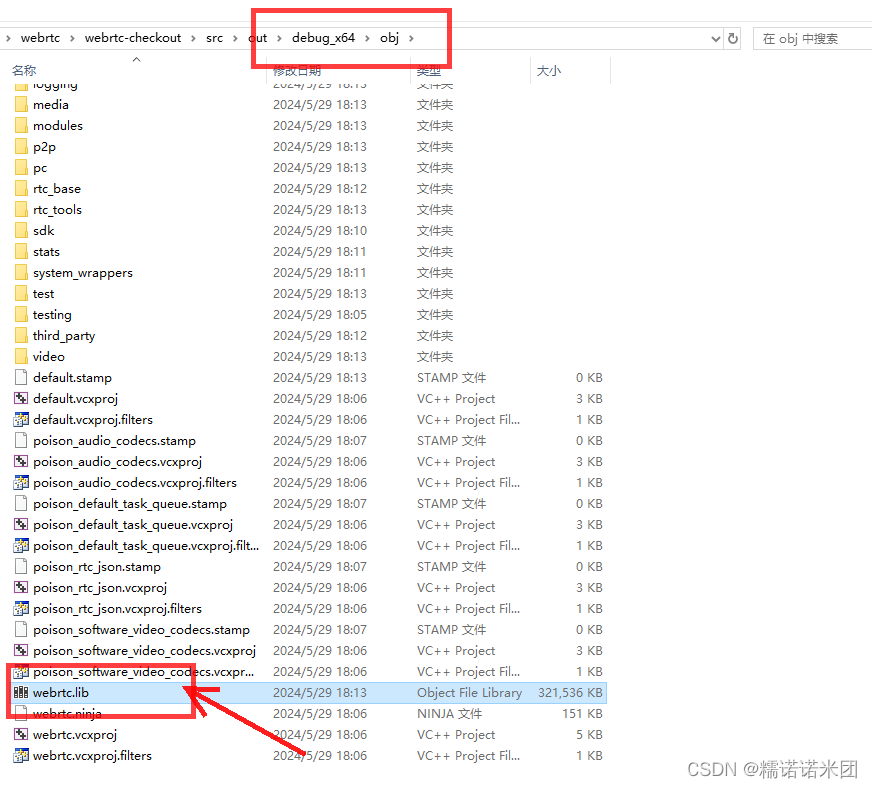
Window下VS2019编译WebRTC通关版
这段时间需要实现这样一个功能,使用WebRTC实现语音通话功能,第一步要做的事情就是编译WebRTC源码,也是很多码友会遇到的问题。 经过我很多天的踩坑终于踩出来一条通往胜利的大路,下面就为大家详细介绍,编译步骤以及踩…...

【云原生 | 60】Docker中通过docker-compose部署kafka集群
🍁博主简介: 🏅云计算领域优质创作者 🏅2022年CSDN新星计划python赛道第一名 🏅2022年CSDN原力计划优质作者 🏅阿里云ACE认证高级工程师 🏅阿里云开发者社区专…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
