Dijkstra求最短路篇二(全网最详细讲解两种方法,适合小白)(python,其他语言也适用)
前言:
Dijkstra算法博客讲解分为两篇讲解,这两篇博客对所有有难点的问题都会讲解,小白也能很好理解。看完这两篇博客后保证收获满满。
第一篇博客讲解朴素Dijkstra算法Dijkstra求最短路篇一(全网最详细讲解两种方法,适合小白)(python,其他语言也适用),本篇博客讲解堆优化Dijkstra算法,两中算法思路大体相同,但时间复杂度有所区别。
- 朴素Dijkstra算法:时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 堆优化Dijkstra算法:时间复杂度 O ( m l o g n ) O(mlogn) O(mlogn)
两篇博客给出的题目内容一样,只有数据规模不一样。
题目:
题目链接:
850. Dijkstra求最短路 II
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围(两题不同处)
1 ≤ n , m ≤ 1.5 × 1 0 5 1≤n,m≤1.5×10^5 1≤n,m≤1.5×105,
图中涉及边长均不小于 0,且不超过 10000。
数据保证:如果最短路存在,则最短路的长度不超过 1 0 9 10^9 109。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路:
算法分析:
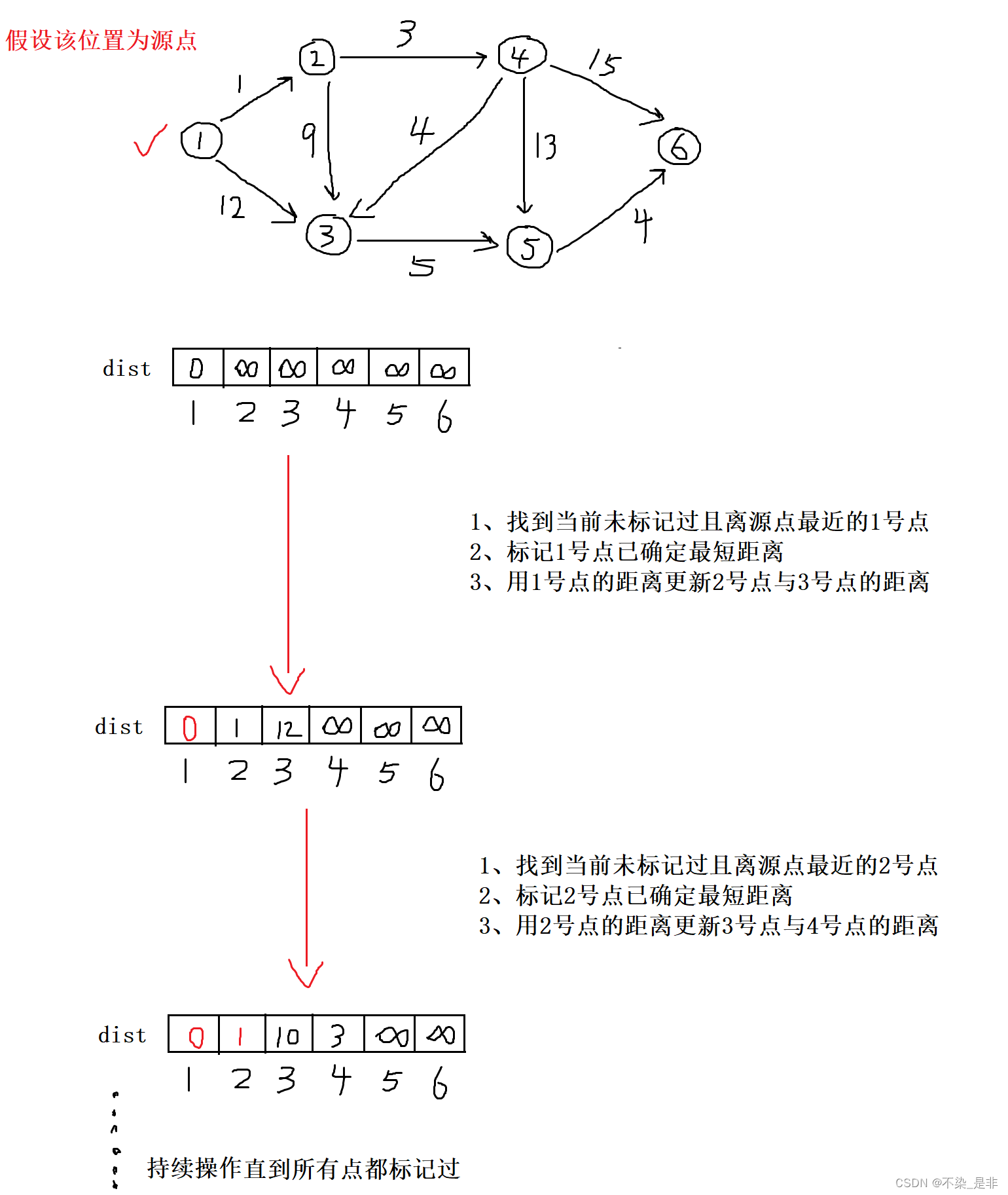
依旧是Dijkstra算法求解,不同的是本题需要降低时间复杂度。
对朴素Dijkstra算法时间复杂度分析可知:
- 寻找路径最短的点: O ( n 2 ) O(n^2) O(n2)
- 加入集合S: O ( n ) O(n) O(n)
- 更新距离: O ( m ) O(m) O(m)
- 所以总的时间复杂度为 O ( n 2 ) O(n^2) O(n2)
所以我们需要对寻找路径最短的点进行改变,如何降低找最短距离的点的时间复杂度呢?
这里可以使用最小堆进行优化(也就是优先队列),对优先队列不太熟悉的可以看看优先队列这篇博客,其他博主写的很详细这里我就不介绍了。
进行优化后时间复杂度分析如下:
- 寻找路径最短的点: O ( n ) O(n) O(n)
- 加入集合S: O ( n ) O(n) O(n)
- 更新距离: O ( m l o g n ) O(mlogn) O(mlogn)
堆的数据结构大家接触的可能有点少,python中有专门的库函数可以直接使用,其他语言也有类似的库函数可以使用。
构造邻接表:
首先对数据进行存储,图的存储有两种方式,一种是邻接表,一种是邻接矩阵。题目中的数据规模用邻接表存储(本题数据规模是稀疏图)。
为什么要用邻接表去存贮,而不是邻接矩阵?
我们采用邻接矩阵还是采用邻接表来表示图,需要判断一个图是稀疏图还是稠密图。稠密图指的是边的条数|E|接近于|V|²,稀疏图是指边的条数|E|远小于于|V|²(数量级差很多)。本题是稠密图,显然稠密图用邻接矩阵存储比较节省空间,反之用邻接表存储。
邻接表存储就不需要注意重边和自环了,因为算法会自动算出最优解
邻接矩阵存储代码如下:
n, m = map(int, input().split()) # 图的节点个数和边数
# 构建邻接表
num = [[] for i in range(n + 1)]
for _ in range(m):a, b, c = map(int, input().split())num[a].append((b, c)) # 无需考虑重边和自环
以题目实例为例,打印num数组
[[], [(2, 2), (3, 4)], [(3, 1)], []]
邻接表构建完成之后就要进行Dijkstra算法,这里直接给出代码,用详细代码给大家进行讲解。整体思路跟朴素Dijkstra算法大致相同
代码及详细注释:
import heapqn, m = map(int, input().split()) # 图的节点个数和边数
# 构建邻接表
num = [[] for i in range(n + 1)]
for _ in range(m):a, b, c = map(int, input().split())num[a].append((b, c)) # 无需考虑重边和自环
dist = [float("inf") for _ in range(n + 1)] # float("inf")在python中是无限大的意思
dist[1] = 0 # 源点到源点的距离为置为 0
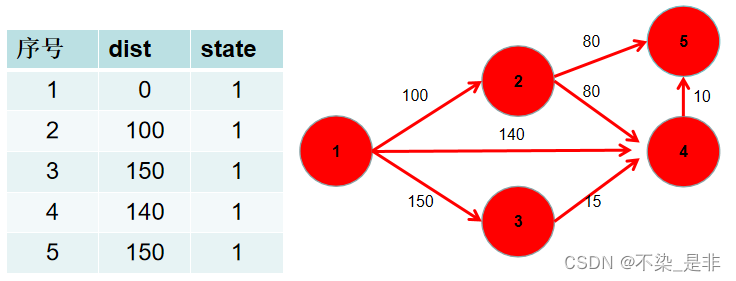
state = [False for i in range(n + 1)] # state 用于记录该点的最短距离是否已经确定def dijstra():# 这里heap中为什么要存两个值呢,首先小根堆是根据距离来排的,所以有一个变量要是距离,# 其次在从堆中拿出来的时候要知道知道这个点是哪个点,不然怎么更新邻接点呢?所以第二个变量要存点。heap = [(0, 1)] # 首先放入距离0和点1,这个顺序不能倒,这里显然要根据距离排序while heap:distance, i = heapq.heappop(heap) # 这里是取出最下距离和对应的点,最小堆自动取出最小值if state[i]: # 如果该点最短距离已经确定,跳过下面操作continuestate[i] = True # 标记该点距离确定for j, d in num[i]: # 循环遍历找点i所能到的点和其距离if dist[j] > distance + d: # 如果原本点j到源点的距离大于后续计算出来的值dist[j] = distance + d # 更新heapq.heappush(heap, (dist[j], j)) # 该点距离和点加入到最小堆中# 判断最后一个点的最短距离是否找到,如果为无穷大,则表示未找到,返回-1,否则返回最短距离dist[-1]if dist[n] == float("inf"):return -1else:return dist[n]print(dijstra())朴素Dijkstra算法大家理解好了本算法也很好理解,操作都是一样,只是在寻找路径最短的点时用了最小堆操作。这里就不拿实例带大家过了,如果略微有点懵,大家可以自己拿实例数据过一遍。
本题主要对 Python 中的 heapq 库进行简略讲解。
import heapqheap = []
heapq.heappush(heap, (1, 2))
heapq.heappush(heap, (1, 3))
heapq.heappush(heap, (2, 1))
heapq.heappush(heap, (2, 0))
heapq.heappush(heap, (0, 2))
heapq.heappush(heap, (0, 0))print("初始状态", heap)
print("删除的元素", heapq.heappop(heap))
print("删除后状态", heap)运行结果:
初始状态 [(0, 0), (1, 2), (0, 2), (2, 0), (1, 3), (2, 1)]
删除的元素 (0, 0)
删除后状态 [(0, 2), (1, 2), (2, 1), (2, 0), (1, 3)]
- heapq.heappush((heap, (1, 2)):把元素(1,2)加入到堆 heap中(每次加入后都是最小堆的构建形式)。
- heapq.heappop(heap):弹出堆顶元素(最小堆的堆顶就是最小元素)。
总结:
堆优化版dijkstra适合稀疏图
思路:
堆优化版的dijkstra是对朴素版dijkstra进行了优化,在朴素版dijkstra中时间复杂度最高的寻找距离
最短的点O(n^2)可以使用最小堆优化。
- 一号点的距离初始化为零,其他点初始化成无穷大。
- 将一号点放入堆中。
- 不断循环,直到堆空。每一次循环中执行的操作为:
弹出堆顶(与朴素版diijkstra找到S外距离最短的点相同,并标记该点的最短路径已经确定)。
用该点更新临界点的距离,若更新成功就加入到堆中。
时间复杂度分析
- 寻找路径最短的点: O ( n ) O(n) O(n)
- 加入集合S: O ( n ) O(n) O(n)
- 更新距离: O ( m l o g n ) O(mlogn) O(mlogn)
相关文章:

Dijkstra求最短路篇二(全网最详细讲解两种方法,适合小白)(python,其他语言也适用)
前言: Dijkstra算法博客讲解分为两篇讲解,这两篇博客对所有有难点的问题都会讲解,小白也能很好理解。看完这两篇博客后保证收获满满。 第一篇博客讲解朴素Dijkstra算法Dijkstra求最短路篇一(全网最详细讲解两种方法,适合小白)(p…...
Dijkstra求最短路篇一(全网最详细讲解两种方法,适合小白)(python,其他语言也适用)
前言: Dijkstra算法博客讲解分为两篇讲解,这两篇博客对所有有难点的问题都会讲解,小白也能很好理解。看完这两篇博客后保证收获满满。 本篇博客讲解朴素Dijkstra算法,第二篇博客讲解堆优化Dijkstra算法Dijkstra求最短路篇二(全网…...

计算机组成原理06:浮点数运算
浮点数加减运算 之前我们提到过,浮点数具有特定的表示形式。因此,在进行浮点数的加减运算之前,需要统一浮点数的表达方式。这里我们主要对浮点数表示中的尾数M进行处理,要求0≤M<1,统一格式如下: 正数…...

opencascade 快速显示AIS_ConnectedInteractive源码学习
AIS_ConcentricRelation typedef PrsDim_ConcentricRelation AIS_ConcentricRelation AIS_ConnectedInteractive 简介 创建一个任意位置的另一个交互对象实例作为参考。这允许您使用连接的交互对象,而无需重新计算其表示、选择或图形结构。这些属性是从您的参考对…...

CentOS系统上安装单机版Redis教程
一、前言 1.1 为什么选择Redis? Redis不仅支持丰富的数据类型(如字符串、哈希、列表、集合、有序集合等),还具有高性能、持久化、发布订阅、事务和Lua脚本等特点。这些优势使其成为分布式系统和高并发应用中的首选。 1.2 为什么…...
纯Java实现Google地图的KMZ和KML文件的解析
目录 前言 一、关于KMZ和KML 1、KMZ是什么 2、KML是什么 二、Java解析实例 1、POM.xml引用 2、KML 基类定义 3、空间对象的定义 4、Kml解析工具类 三、KML文件的解析 1、KML解析测试 2、KMZ解析测试 四、总结 前言 今天是六.一儿童节,在这里祝各位大朋友…...

k8s自定义资源你会创建吗
创建自定义资源定义 CustomResourceDefinition 当你创建新的 CustomResourceDefinition(CRD)时,Kubernetes API 服务器会为你所 指定的每一个版本生成一个 RESTful 的 资源路径。CRD 可以是名字空间作用域的,也可以是集群作用域的…...
CATIA二次开发VBA入门(4)——进程外开发环境搭建,vb.net在Visual Studio中开发,创建圆柱曲面的宏录制到二次开发案例
目录 引出vb.net和vb6.0 进程外开发环境搭建vb.net开发环境搭建《CATIA二次开发技术基础》模板 添加宏库引用 vs开发环境初步vs中的立即窗口对象浏览器 建立模板案例:创建一堆圆柱曲面第一步:录制宏第二步:代码精简第三步:for循环…...

c++字符串相关接口
c字符串相关接口 1.str2wstr(str转换wstr)2.wstr2str(str转换wstr)3.Utf8ToAsi(Utf8转换ANSI)4.AsiToUtf8(ANSI转换Utf8)5.stringformatA/stringformatW(按照指定的格式格式化字符串)6.GetStringBetween(获取cStart cEnd之间的字符串)7.Char2Int(char转int)8.Str2Bin(字符串转换…...
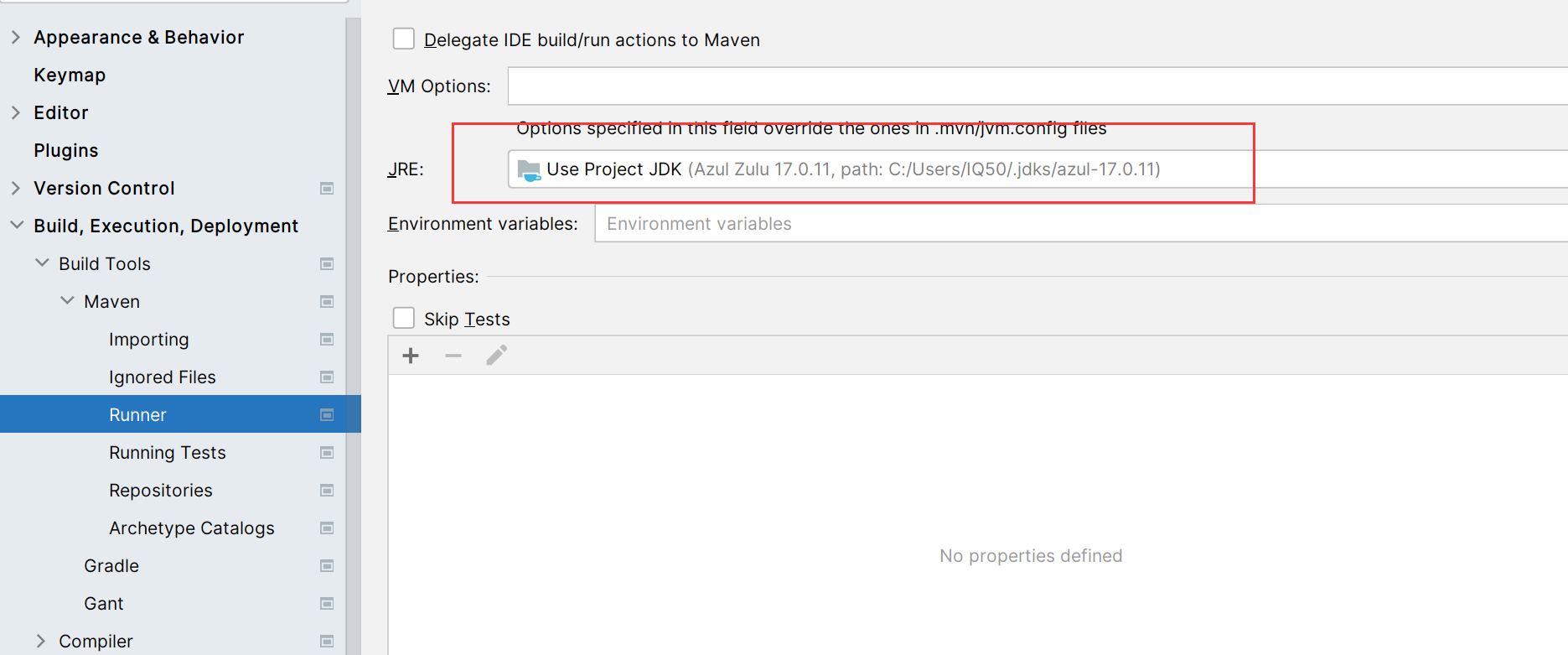
Maven打包错误:无效的源发行版:17
1. 报错问题 在用maven进行打包时(clean & install),报如下错误: 一开始让我很摸不着头脑,我确定我的pom.xml,还有IDEA中的Project Settings是正确的。 2. 排查 尽管确定,但还是一个个排…...

【环境栏Composer】Composer常见问题(持续更新)
1、执行composer install提示当前目录中没有 composer.lock 文件时 No composer.lock file present. Updating dependencies to latest instead of installing from lock file. See https://getcomposer.org/install for more information. Composer 在执行 install 命令时会…...

塑造更智慧的AI:策略与路径探索
提升数据质量: 数据清洗:去除数据中的异常值、缺失值、噪声等干扰因素,确保数据的准确性和一致性。数据标注:为数据集提供准确的标签,以便进行有监督学习。标注的质量直接影响模型的性能。数据增强:通过图像…...

软设之快速排序
快速排序是冒泡排序的改进算法 它采用的是分治法,基本思想是把原问题分解为若干规模更小但结构与原问题相似的子问题,通过递归解决这些子问题,然后将这些子问题的解组合成原问题的解。 它的步骤是 1.在待排序的n个记录中任取一个记录&…...

从零学算法2965
2965. 找出缺失和重复的数字 给你一个下标从 0 开始的二维整数矩阵 grid,大小为 n * n ,其中的值在 [1, n2] 范围内。除了 a 出现 两次,b 缺失 之外,每个整数都 恰好出现一次 。 任务是找出重复的数字a 和缺失的数字 b 。 返回一个…...
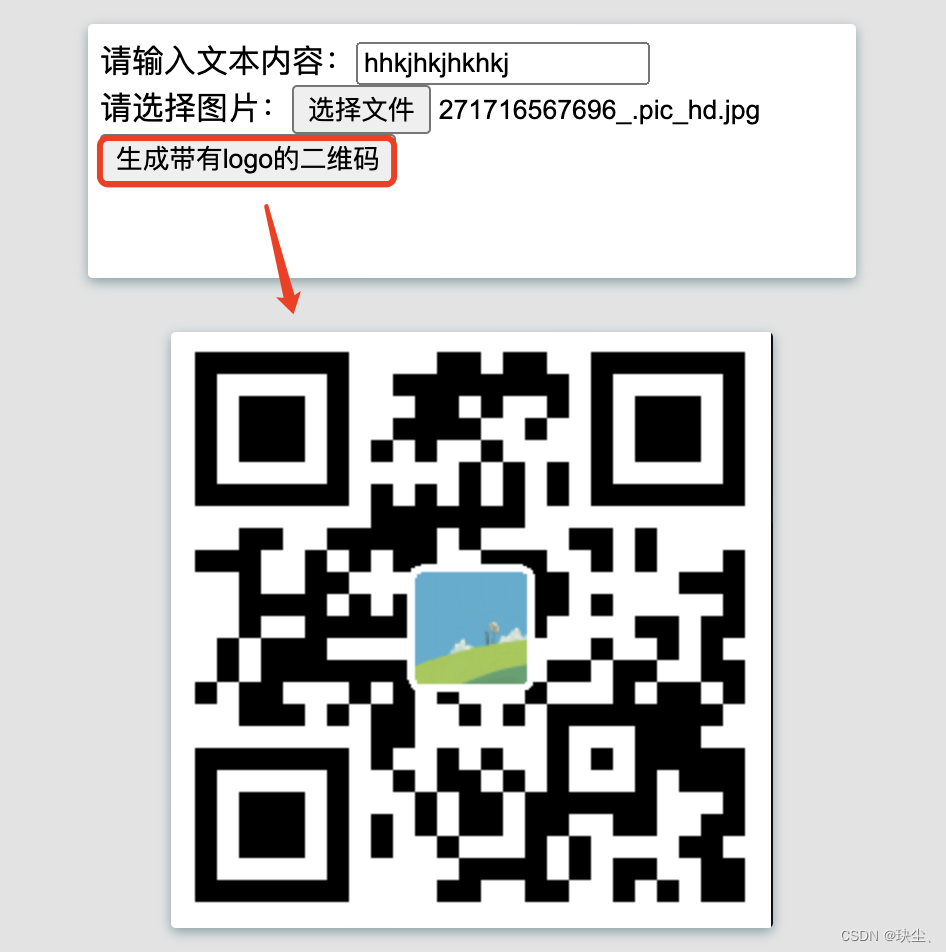
【Mac版】Java生成二维码
软件版本 IntelliJ IDEA:2023.2 JDK:17 Tomcat:10.1.11 Maven:3.9.3 技术栈 servlet谷歌的:zxing 生成普通的黑白二维码在二维码中间添加一个小图标 github开源项目:qrcode qrcode开源项目的内部是基于z…...

ROS2自定义服务接口
ROS2自定义服务接口 在src/village_interface 下构建srv文件夹 src/village_interface/srv 下新建一个BorrowMoney.srv 遵循大小写编程规范 # 客户端请求 string name uint32 money # 中间这三个横杠很重要 不能删掉 --- # 服务端响应 bool success uint32 money接口编译 修改…...
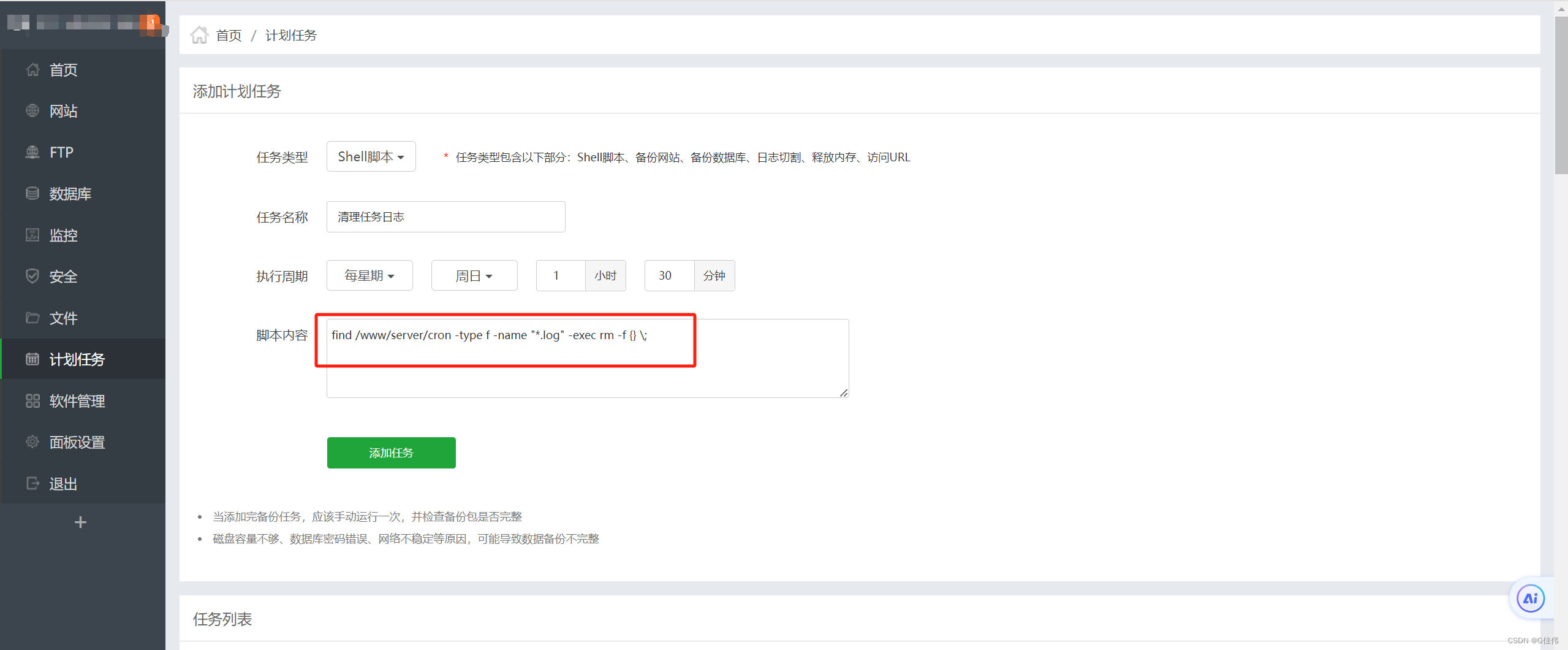
linux /www/server/cron内log文件占用空间过大,/www/server/cron是什么内容,/www/server/cron是否可以删除
linux服务器长期使用宝塔自带计划任务,计划任务执行记录占用服务器空间过大,导致服务器根目录爆满,需要长期排查并删除 /www/server/cron 占用空间过大问题处理 /www/server/cron是什么内容?/www/server/cron是否可以删除…...

C++青少年简明教程:break语句、continue语句
C青少年简明教程:break语句、continue语句 break语句 只能用在switch语句和循环语句(for循环、while循环和do-while循环)中。作用:跳出switch语句或提前终止循环。 break语句的基本语法如下: break; break语句的示例…...
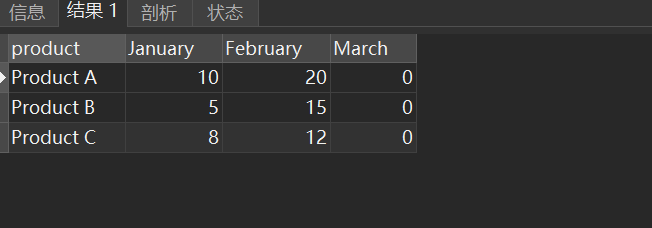
MySQL实战行转列(或称为PIVOT)实战sales的表记录了不同产品在不同月份的销售情况,进行输出
有一个sales的表,它记录了不同产品在不同月份的销售情况: productJanuaryFebruaryMarchProduct AJanuary10Product AFebruary20Product BJanuary5Product BFebruary15Product CJanuary8Product CFebruary12 客户需求展示为如下的样子: pro…...

牛客NC164 最长上升子序列(二)【困难 贪心+二分 Java/Go/PHP/C++】
题目 题目链接: https://www.nowcoder.com/practice/4af96fa010c44638a7e112abf65f7237 思路 贪心二分 所谓贪心,就是往死里贪,所以对于最大上升子序列,结尾元素越小,越有利于后面接上其他的数,也就可能变…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
