【论文复现|智能算法改进】融合黑寡妇思想的蜣螂优化算法
目录
- 1.算法原理
- 2.改进点
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.算法原理
【智能算法】蜣螂优化算法(DBO)原理及实现
2.改进点
ICMIC混沌映射
z n + 1 = sin ( α z n ) , α ∈ ( 0 , + ∞ ) (1) z_{n+1}=\sin(\frac{\alpha}{z_n}),\alpha\in(0,+\infty)\tag{1} zn+1=sin(znα),α∈(0,+∞)(1)
α 是映射系数, 为了进一步探索映射参数的影响, 采用李雅普诺(lyapunov)指数(λ)来衡量映射效果。李雅普诺夫指数表征了一个系统随着时间运动发生改变的程度,当指数小于 0,说明运动系统体积缩小,系统趋于稳定;而当指数大于 0,则说明运动系统体积增大,系统趋于混沌。
λ = lim n → ∞ 1 n ∑ n = 0 n − 1 ln ∣ d f ( z n , α ) d z ∣ (2) \lambda=\lim_{n\to\infty}\frac{1}{n}\sum_{n=0}^{n-1}\ln|\frac{df(z_n,\alpha)}{dz}|\tag{2} λ=n→∞limn1n=0∑n−1ln∣dzdf(zn,α)∣(2)
论文中给出李雅普诺夫指数图
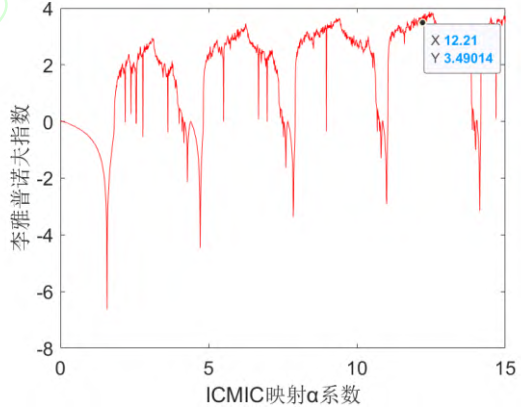
复现一下这张图
黑寡妇算法
论文提出使用黑寡妇算法替换滚球行为算法。 黑寡妇算法将黑寡妇蜘蛛在蛛网中的运动模型转化为线性和螺旋两种形式,位置更新公式:
x i ( t + 1 ) = { x ∗ ( t ) − m x r 1 ( t ) if α ≤ 0.3 x ∗ ( t ) − cos ( 2 π β ) x i ( t ) α > 0.3 (3) x_i(t+1)=\begin{cases}x^*(t)-mx_{r_1}(t)&\text{if}~\alpha\leq0.3\\x^*(t)-\cos(2\pi\beta)x_i(t)&\alpha>0.3\end{cases}\tag{3} xi(t+1)={x∗(t)−mxr1(t)x∗(t)−cos(2πβ)xi(t)if α≤0.3α>0.3(3)
信息素(pheromone)是黑寡妇种群的另一个特质,在交配的过程中起到了重要的作用。黑寡妇算法将信息素定义为:
p h e r o m o n e ( i ) = f i t n e s s max − f i t n e s s ( i ) f i t n e s s max − f i t n e s s min (4) pheromone(i)=\frac{fitness_{\max}-fitness(i)}{fitness_{\max}-fitness_{\min}}\tag{4} pheromone(i)=fitnessmax−fitnessminfitnessmax−fitness(i)(4)
当信息素过小时,个体将会被新个体替代,位置更新:
x i ( t ) = x ∗ ( t ) + 1 2 [ x r 1 ( t ) − ( − 1 ) σ ∗ x r 2 ( t ) ] (5) x_i(t)=x^*(t)+\frac{1}{2}[x_{r_1}(t)-(-1)^\sigma*x_{r_2}(t)]\tag{5} xi(t)=x∗(t)+21[xr1(t)−(−1)σ∗xr2(t)](5)
自适应 T 分布改进因子
采用以迭代次数自由度参数的t 分布变异扰动因子,对小蜣螂觅食行为进行扰动。t分布即是学生分布,决策参数为自由度参数 m,其概率密度函数为:
p ( x ) = Γ ( m + 1 2 ) m π ∗ Γ ( m 2 ) ∗ ( 1 + x 2 m ) − m + 1 2 , − ∞ < x , ∞ (6) p(x)=\frac{\Gamma(\frac{m+1}{2})}{\sqrt{m\pi} ^*\Gamma(\frac{m}{2})}*(1+\frac{x^2}{m})^{^{-\frac{m+1}{2}}},-\infty<x,\infty \tag{6} p(x)=mπ∗Γ(2m)Γ(2m+1)∗(1+mx2)−2m+1,−∞<x,∞(6)
当 m=1 时, t 分布即是柯西分布, m 趋于无穷, t 分布即是高斯分布。因此自适应 t 分布变异扰动因子具有柯西、高斯分布两种特性,使得蜣螂算法在迭代前期具有较好的全局开发能力,在迭代后期具有良好的局部探索能力,并提高算法的收敛速度。位置更新:
x i ( t ) = X b + t { exp [ 4 ∗ ( t M ) 2 ] } ∗ X b (7) x_i(t)=X^b+t\{\exp[4^*(\frac{t}{M})^2]\}^*X^b\tag{7} xi(t)=Xb+t{exp[4∗(Mt)2]}∗Xb(7)
流程图

3.结果展示
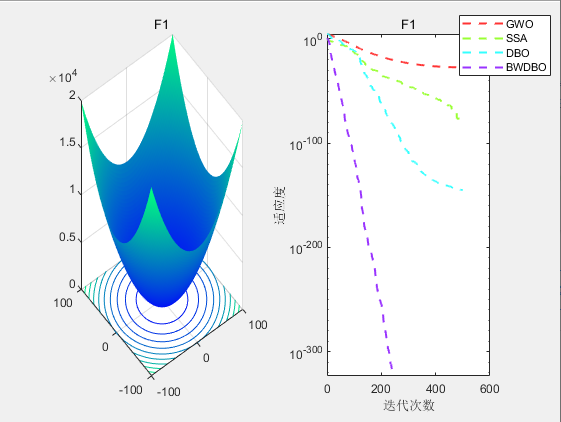
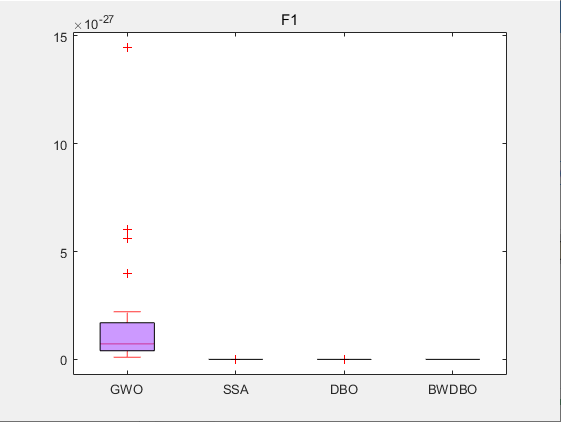
采用CEC2005测试集测试对GWO,SSA,DBO,BWDBO算法进行测试对比:

CEC2005-F1
CEC2005-F1 箱型图
CEC2005-F1 Friedamn排名

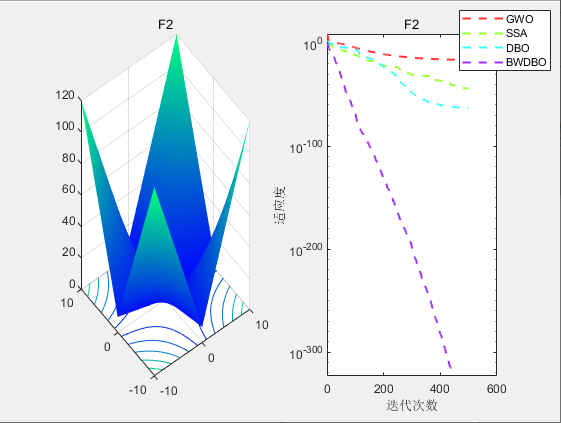
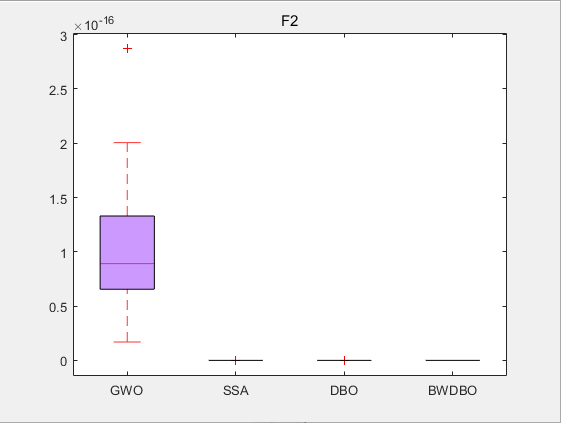
**CEC2005-F2 **

**CEC2005-F3 **
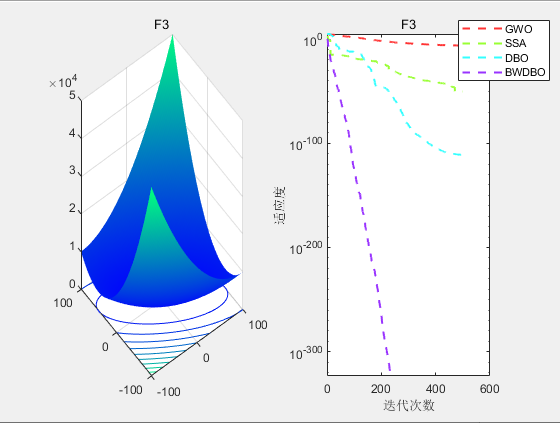
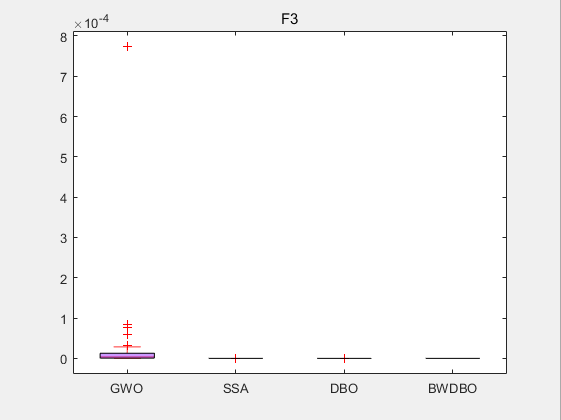

**CEC2005-F3 **
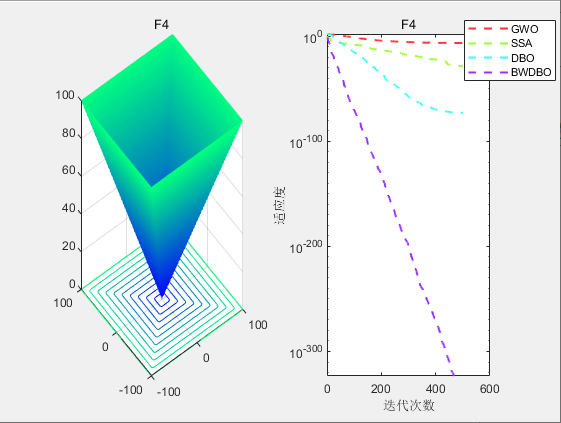
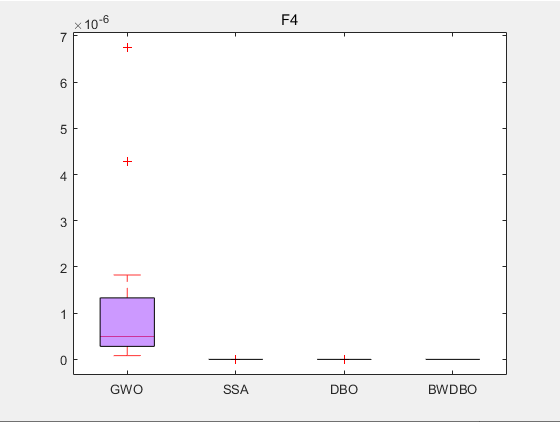
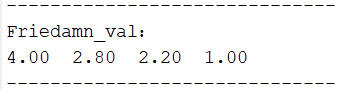
从适应度曲线,箱型图,Friedamn排名来看,改进蜣螂优化算法DWBDO效果不错😊
4.参考文献
[1] 孔令崧,石颉,孙浩,等.融合黑寡妇思想的蜣螂优化算法[J/OL].微电子学与计算机,1-15[2024-06-01].
5.代码获取
智能算法,论文复现,算法应用(机器学习、二维&三维路径规划、UAV路径规划、布局优化、调度优化、VRP问题等),定制算法可以联系我~
资源清单:https://docs.qq.com/sheet/DU1V0QWtSeHJnY0JU?u=989d90f9b14449ec9419aa7b51473c1b&tab=BB08J2
相关文章:

【论文复现|智能算法改进】融合黑寡妇思想的蜣螂优化算法
目录 1.算法原理2.改进点3.结果展示4.参考文献5.代码获取 1.算法原理 【智能算法】蜣螂优化算法(DBO)原理及实现 2.改进点 ICMIC混沌映射 z n 1 sin ( α z n ) , α ∈ ( 0 , ∞ ) (1) z_{n1}\sin(\frac{\alpha}{z_n}),\alpha\in(0,\infty)\ta…...
Unity + 雷达 粒子互动(待更新)
效果预览: 花海(带移动方向) VFX 实例 脚本示例 使用TouchScript,计算玩家是否移动,且计算移动方向 using System.Collections; using System.Collections.Generic; using TouchScript; using TouchScript.Pointers; using UnityEngine; using UnityEngine.VFX;public …...

英语翻译程序,可以对用户自己建立的词汇表进行增删查改
⑴ 自行建立一个包含若干英文单词的词汇表文件,系统初始化时导入内存,用于进行句子翻译。 ⑵ 用户可以输入单词或者句子,在屏幕上显示对应翻译结果。 ⑶ 用户可对词汇表进行添加和删除,并能将更新的词汇表存储到文件中。 #defi…...

Django ORM魔法:用Python代码召唤数据库之灵!
探索Django ORM的神奇世界,学习如何用Python代码代替复杂的SQL语句,召唤数据库之灵,让数据管理变得轻松又有趣。从基础概念到高级技巧,阿佑带你一步步成为Django ORM的魔法师,让你的应用开发速度飞起来! 文…...

JetBrains Mono字体下载及安装
百度云字体下载 提取码:zida 1.mac 安装 选择文件夹中的所有字体文件,然后双击它们。点击“安装字体”按钮。 2.windows 安装 选择文件夹中的字体文件,右键单击其中任何一个,然后从菜单中选择“安装”。 3.linux 安装 将字体…...

【OS】AUTOSAR OS系统调用产生Trap的过程详解
目录 前言 正文 1.Os_Hal_Trap使用示例 2. Os_Hal_Trap的定义 3. syscall详解详解...

Java中的异常处理机制
在Java中,异常处理是一种重要的编程机制,用于处理程序运行时可能出现的错误情况。它提供了一种结构化的方式来处理异常情况,使程序能够更健壮、更易于维护。下面将从技术难点、面试官关注点、回答吸引力和代码举例四个方面来详细描述Java中的…...

什么是PLAB?
接上文PLAB---》 可以看到和TLAB很像,PLAB即 Promotion Local Allocation Buffers。用在年轻代对象晋升到老年代时。 在多线程并行执行YGC时,可能有很多对象需要晋升到老年代,此时老年代的指针就"热"起来了,于是搞了个…...
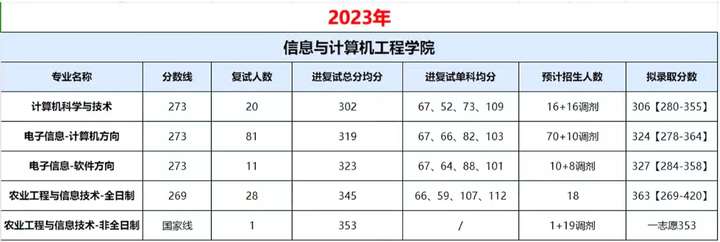
复试不考机试,初试300分以上,上岸稳了?东北林业大学计算机考研考情分析!
东北林业大学(Northeast Forestry University),简称东北林大(NEFU),位于黑龙江省哈尔滨市,是一所以林科为优势、林业工程为特色的中华人民共和国教育部直属高校,由教育部、国家林业局…...
【30天精通Prometheus:一站式监控实战指南】第12天:windows_exporter从入门到实战:安装、配置详解与生产环境搭建指南,超详细
亲爱的读者们👋 欢迎加入【30天精通Prometheus】专栏!📚 在这里,我们将探索Prometheus的强大功能,并将其应用于实际监控中。这个专栏都将为你提供宝贵的实战经验。🚀 Prometheus是云原生和DevOps的…...

微信小程序的事件绑定方式
微信小程序的事件绑定方式主要包括以下几种,每种方式都有其特定的用法和特性: 基础绑定方式: bind:这是最基础的绑定方式,用于绑定事件处理函数。例如,bindtap用于绑定点击事件。当组件触发事件时…...
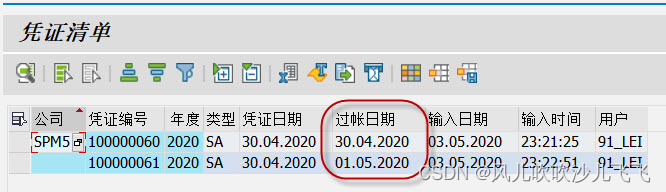
AR和AP重分类(Regroup)[FAGLF101/OBBU/OBBV]
一、为什么AR和AP科目需要重分类 1.1 执行操作的前提(重要) 存在AR的当月总余额在贷方(客户贷项凭证、预收账款等)或AP的当月总余额在借方(供应商贷项凭证、预收账款等),这种情况下无法真实的反映出资产和负债情况&…...
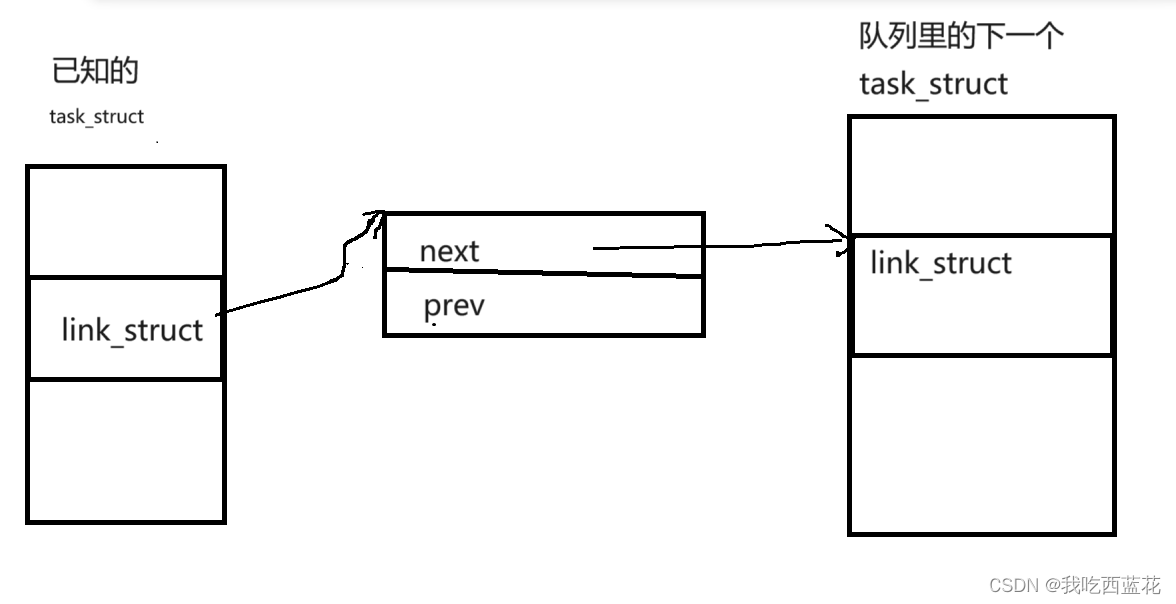
进程——linux
目录 冯诺依曼体系结构(计算机组成原理与体系结构) 关于冯诺依曼,必须强调几点: 操作系统(Operator System) 概念 设计OS的目的 定位 如何理解 "管理" 总结 系统调用和库函数概念 承上启下 一、进程 基本概念…...

关于如何通过APlayer+MetingJS为自己的wordpress博客网页添加网易音乐播放器(无需插件)
本文转自博主的个人博客:https://blog.zhumengmeng.work,欢迎大家前往查看。 原文链接:点我访问 序言:最近在网上冲浪,发现大家的博客大部分都有一个音乐播放器能够播放音乐,随机我也开始寻找解决方法。可是找来找去我…...

架构师如何以打游戏的心态做开发?
为什么打游戏可以很好玩,能够自发学习,从青铜到黄金很简单。换个角度思考🤔,以打游戏的心态如何进行架构开发,可以采用以下策略: 设定目标和里程碑: 就像游戏中的任务和关卡一样,为…...

【WP|6】WordPress 主题开发详解
WordPress主题开发是打造独特、功能强大的网站的重要途径。无论是创建全新的主题还是对现有主题进行自定义,掌握主题开发技能都是非常重要的。本文将详细讲解 WordPress 主题开发的基本步骤、文件结构、模板层次以及一些高级技巧,帮助你从零开始创建一个…...
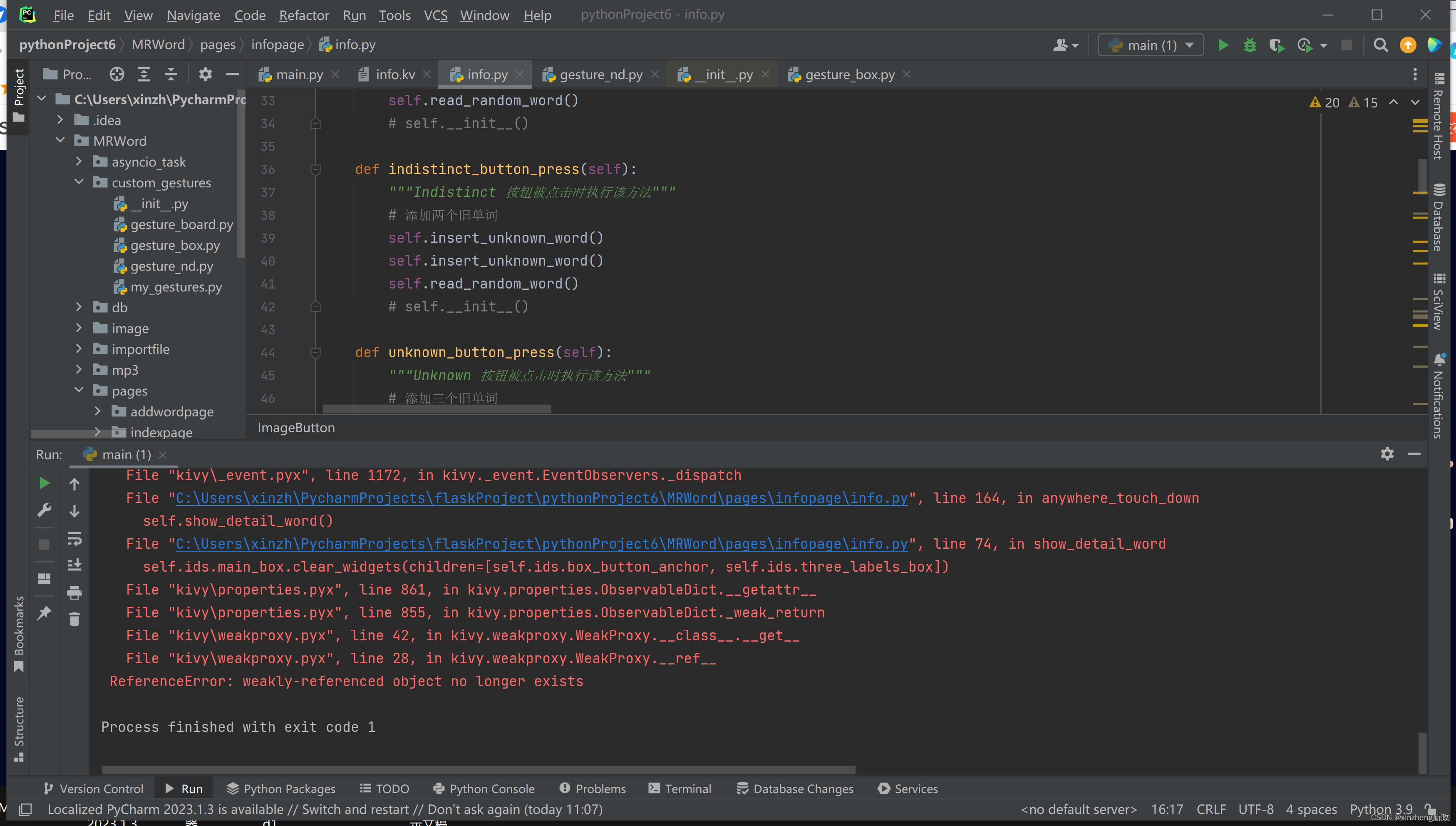
Kivy.garden.NavigationDrawer 后续学习
如百词斩部分代码 MRWord\pages\infopage\info.kv <InfoPage>:anim_type: slide_above_simpleid: main_winbox_button_anchor: box_button_anchor.__self__three_labels_box: three_labels_box.__self__box_phonetic: box_phonetic.__self__BoxLayout:BoxLayout:id: ma…...

【CVE-2021-3156】——漏洞复现、原理分析以及漏洞修复
文章目录 前言1、漏洞概述2、漏洞复现2.1、漏洞复现测试环境2.2、漏洞复现具体步骤 3、漏洞原理3.1、前置知识3.1.1、sudo3.1.2、sudoedit3.1.3、转义字符 3.2、漏洞分析 4、漏洞修复5、参考文献总结 前言 2021年01月27日,RedHat官方发布了Sudo缓冲区/栈溢出漏洞的风…...

Github 2024-05-31 Java开源项目日报 Top10
根据Github Trendings的统计,今日(2024-05-31统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Java项目10TypeScript项目1JavaGuide - Java 程序员学习和面试指南 创建周期:2118 天开发语言:Java协议类型:Apache License 2.0Star数量:1…...

【上海大学计算机组成原理实验报告】六、内存系统实验
一、实验目的 学习内存访问机制。理解代码和数据的分区存放原理和技术。 二、实验原理 根据实验指导书的相关内容,地址寄存器MAR用来存放要进行读或写的存储器EM的地址。其内容经数据总线DBUS写入,因此必须在数据总线上具有数据后,配合MAR允…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...

WinUI3开发_使用mica效果
简介 Mica(云母)是Windows10/11上的一种现代化效果,是Windows10/11上所使用的Fluent Design(设计语言)里的一个效果,Windows10/11上所使用的Fluent Design皆旨在于打造一个人类、通用和真正感觉与 Windows 一样的设计。 WinUI3就是Windows10/11上的一个…...
