图形学初识--屏幕空间变换
文章目录
- 前言
- 正文
- 为什么需要屏幕空间变换?
- 什么是屏幕空间变换?
- 屏幕空间变换矩阵如何推导?
- 问题描述
- 步骤描述
- 结尾:喜欢的小伙伴点点关注+赞哦!
前言
前面章节主要讲解了视图变换和投影变换,此时距离在屏幕空间显示也就只差一步之遥了,只需要将NDC坐标转换为屏幕空间坐标即可!有了前面一些章节的学习,相信大家对于本章节的学习还是很容易的!
正文
为什么需要屏幕空间变换?
因为经过了视图变换和投影变换后,咱们已经将所有的顶点坐标转换成了NDC坐标,也就是x/y/z的范围都在 [ − 1 , 1 ] [-1,1] [−1,1] 的坐标,但是正常咱们得电脑屏幕的XY坐标范围一般都是 [ 0 , w i d t h − 1 ] × [ 0 , h e i g h t − 1 ] [0,width-1] \times [0, height-1] [0,width−1]×[0,height−1] ,所以咱们需要屏幕空间变换!
什么是屏幕空间变换?
本质上和之前的视图变换、投影变换并无不同,就是一个矩阵罢了!
屏幕空间变换矩阵如何推导?
问题描述
将x坐标由 [ − 1 , 1 ] [-1,1] [−1,1] 变换为 $ [0,screen_width - 1]$ ,将y坐标由 [ − 1 , 1 ] [-1,1] [−1,1] 变换为 $ [0,screen_height - 1]$ ,将z坐标由 [ − 1 , 1 ] [-1,1] [−1,1] 变换为 $ [0,1]$.
如下图所示:

步骤描述
步骤1:将xyz坐标变换到 [ 0 , 1 ] [0,1] [0,1] 的范围
步骤2:将xy坐标缩放至 [ 0 , s c r e e n w i d t h − 1 ] × [ 0 , s c r e e n h e i g h t − 1 ] [0, screen_width - 1] \times [0, screen_height - 1] [0,screenwidth−1]×[0,screenheight−1]
咱们先思考下步骤1如何实现呢?当前的xyz坐标范围为 [ − 1 , 1 ] [-1,1] [−1,1] ,目标的坐标范围为 [ 0 , 1 ] [0,1] [0,1] ,如何做呢?
这时候其实咱们分两步:
第一步:将 [ − 1 , 1 ] [-1,1] [−1,1] 缩放至 [ − 0.5 , 0.5 ] [-0.5,0.5] [−0.5,0.5] 的范围。
第二步:将 [ − 0.5 , 0.5 ] [-0.5,0.5] [−0.5,0.5] 沿着对应轴轴方向移动0.5单位即可。
于是咱们分别得到缩放矩阵和平移矩阵如下:
S = [ 0.5 0 0 0 0 0.5 0 0 0 0 0.5 0 0 0 0 1 ] S = \begin{bmatrix} 0.5&0&0&0\\ 0&0.5&0&0\\ 0&0&0.5&0\\ 0&0&0&1\\ \end{bmatrix} S= 0.500000.500000.500001
T = [ 0 0 0 0.5 0 0 0 0.5 0 0 0 0.5 0 0 0 1 ] T = \begin{bmatrix} 0&0&0&0.5\\ 0&0&0&0.5\\ 0&0&0&0.5\\ 0&0&0&1\\ \end{bmatrix} T= 0000000000000.50.50.51
于是咱们只需要将两者相乘,即可获得相应的结果:
M 1 = T ∗ S = [ 0.5 0 0 0.5 0 0.5 0 0.5 0 0 0.5 0.5 0 0 0 1 ] M_1 = T * S = \begin{bmatrix} 0.5&0&0&0.5\\ 0&0.5&0&0.5\\ 0&0&0.5&0.5\\ 0&0&0&1\\ \end{bmatrix} M1=T∗S= 0.500000.500000.500.50.50.51
然后咱们思考下步骤二,当前的xy坐标范围为: [ 0 , 1 ] [0,1] [0,1] ,目标范围为 $[0,screen_width-1] 和 [0,screen_height-1] $
这个问题也就只是个xy轴的缩放问题而已,很容易得到以下缩放矩阵:
M 2 = [ s c r e e n _ w i d t h 0 0 0 0 s c r e e n _ h e i g h t 0 0 0 0 1 0 0 0 0 1 ] M_2 = \begin{bmatrix} screen\_width&0&0&0\\ 0&screen\_height&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} M2= screen_width0000screen_height0000100001
然后咱们将步骤一的结果和步骤二的结果结合起来即可得到最终的屏幕空间变换矩阵,如下:
M s c r e e n = M 2 ∗ M 1 = M 2 = [ 0.5 ∗ s c r e e n _ w i d t h 0 0 0.5 ∗ s c r e e n _ w i d t h 0 0.5 ∗ s c r e e n _ h e i g h t 0 0.5 ∗ s c r e e n _ h e i g h t 0 0 0.5 0.5 0 0 0 1 ] M_{screen}= M_2 * M_1 = M_2 = \begin{bmatrix} 0.5*screen\_width&0&0&0.5*screen\_width\\ 0&0.5*screen\_height&0&0.5*screen\_height\\ 0&0&0.5&0.5\\ 0&0&0&1\\ \end{bmatrix} Mscreen=M2∗M1=M2= 0.5∗screen_width00000.5∗screen_height00000.500.5∗screen_width0.5∗screen_height0.51
于是大功告成啦!咱们成功的将NDC坐标转换成了屏幕空间坐标!
结尾:喜欢的小伙伴点点关注+赞哦!
你们的点赞就是我创作的最大动力!希望对各位小伙伴能够有所帮助哦,永远在学习的道路上伴你而行, 我是航火火,火一般的男人!
相关文章:

图形学初识--屏幕空间变换
文章目录 前言正文为什么需要屏幕空间变换?什么是屏幕空间变换?屏幕空间变换矩阵如何推导?问题描述步骤描述 结尾:喜欢的小伙伴点点关注赞哦! 前言 前面章节主要讲解了视图变换和投影变换,此时距离在屏幕空间显示也就…...

爬楼梯 - LeetCode 热题 81
大家好!我是曾续缘😇 今天是《LeetCode 热题 100》系列 发车第 81 天 动态规划第 1 题 ❤️点赞 👍 收藏 ⭐再看,养成习惯 爬楼梯 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法…...

详解 Spark 核心编程之 RDD 分区器
一、RDD 分区器简介 Spark 分区器的父类是 Partitioner 抽象类分区器直接决定了 RDD 中分区的个数、RDD 中每条数据经过 Shuffle 后进入哪个分区,进而决定了 Reduce 的个数只有 Key-Value 类型的 RDD 才有分区器,非 Key-Value 类型的 RDD 分区的值是 No…...

Selenium番外篇文本查找、元素高亮、截图、无头运行
Selenium根据文本查找元素 python def find_element_with_text(self, loc, attribute, text):try:WebDriverWait(self.driver, 5).until(EC.all_of(EC.text_to_be_present_in_element_attribute(loc, attribute, text)))element self.driver.find_element(*loc)if isinsta…...
Java 22的FFM API,比起Java 21的虚拟线程
哪个对Java未来的发展影响更大?两个 Java 版本中的重要特性:Java 21 的虚拟线程和 Java 22 的 FFM API。我这里有一套编程入门教程,不仅包含了详细的视频讲解,项目实战。如果你渴望学习编程,不妨点个关注,给…...

用c语言实现简易三子棋
本篇适用于C语言初学者。 目录 完整代码: 分步介绍: 声明: 代码主体部分: 模块功能实现: 完整代码: #include<stdio.h> #include <stdlib.h> #include <time.h>#define ROW 3 #d…...
)
2024年华为OD机试真题-执行时长-Python-OD统一考试(C卷D卷)
2024年OD统一考试(D卷)完整题库:华为OD机试2024年最新题库(Python、JAVA、C++合集) 题目描述: 为了充分发挥GPU算力,需要尽可能多的将任务交给GPU执行,现在有一个任务数组,数组元素表示在这1秒内新增的任务个数且每秒都有新增任务,假设GPU最多一次执行n个任务,一次执…...
对未知程序所创建的 PDF 文档的折叠书签层级全展开导致丢签的一种解决方法
对需要经常查阅、或连续长时间阅读的带有折叠书签的 PDF 文档展开书签层级,提高阅览导航快捷是非常有必要的。 下面是两种常用书签层级全展开的方法 1、 FreePic2Pdf 1 - 2 - 3 - 4 - 5 - 6,先提取后回挂 2、PdgCntEditor 载入后,直接保存…...
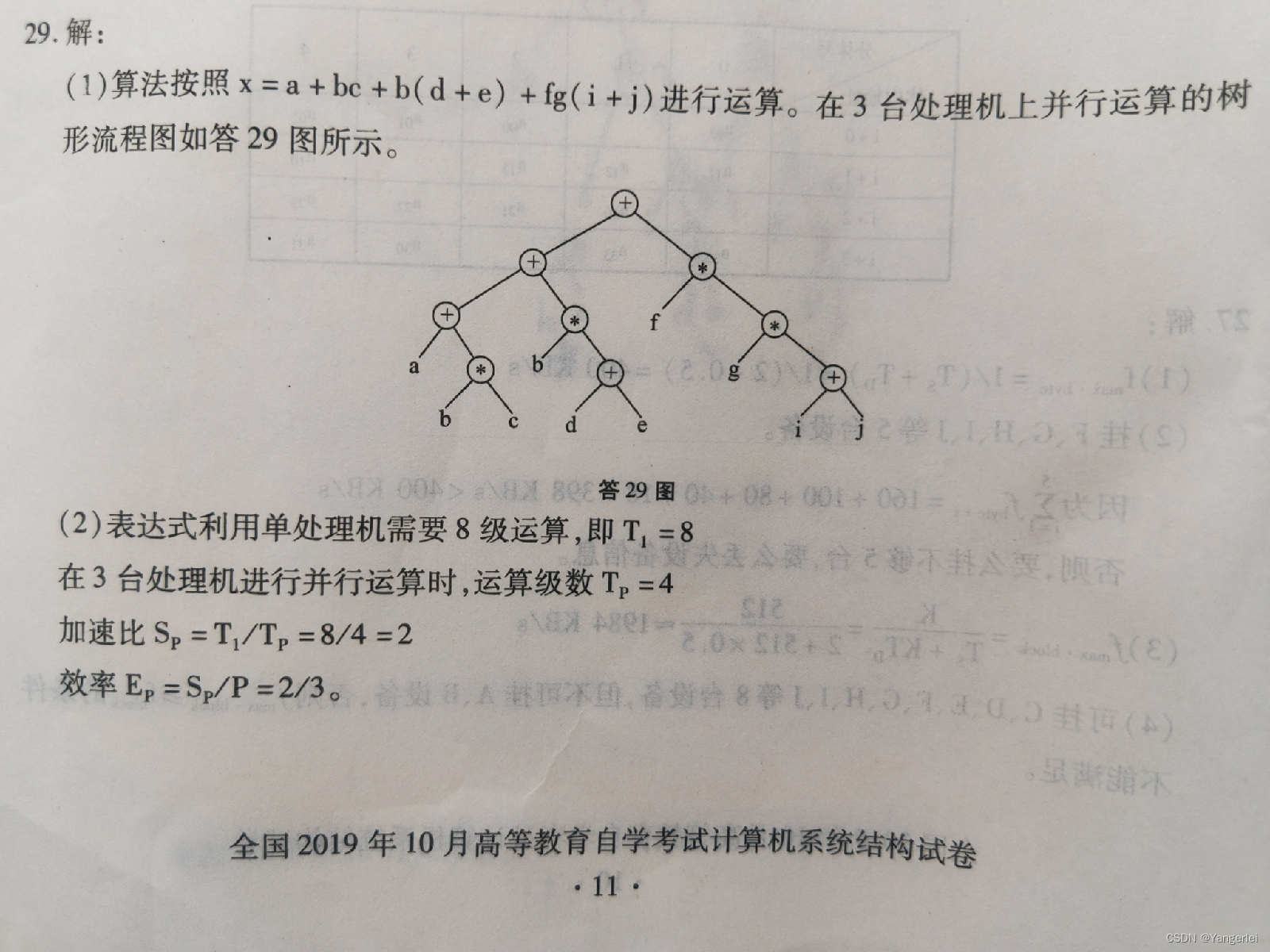
计算机系统结构之FORK和JOIN
程序语言中用FORK语句派生并行任务,用JOIN语句对多个并发任务汇合。 FORK语句的形式为FORK m,其中m为新领程开始的标号。 JOIN语句的形式为JOIN n,其中n为并发进程的个数。 例1:给定算术表达式ZEA*B*C/DF经并行编译得到如下程序…...

Yocto - virtual/kernel介绍
在 Yocto 项目中,"virtual/kernel "是一个虚拟目标,作为 Linux 内核的抽象层。它是一种以灵活方式指定内核依赖关系的方法,允许实际的内核配方由特定构建中使用的机器配置和层决定。 下面是关于 "virtual/kerne"的含义和…...

如何在 DigitalOcean 云服务器上创建自定义品牌名称服务器
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 介绍 对于托管提供商或转售商来说,拥有自定义的名称服务器可以为客户提供更专业的外观。这消除了要求客户将其域名指向另一…...
心链6----开发主页以及后端数据插入(多线程并发)定时任务
心链 — 伙伴匹配系统 开发主页 信息搜索页修改 主页开发(直接list用户) 在后端controller层编写接口去实现显示推荐页面的功能 /*** 推荐页面* param request* return*/GetMapping("/recommend")public BaseResponse<List<User>&…...
【Linux】日志管理
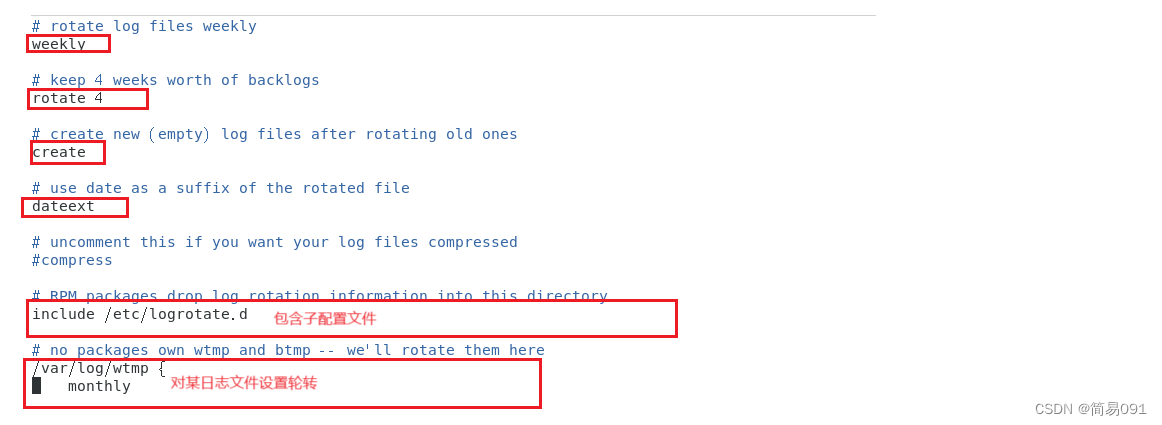
一、日志进程 1、处理日志的进程 rsyslogd:系统专职日志程序 观察rsyslogd程序: ps aux | grep rsyslogd 2、常见的日志文件 1、系统主日志文件: /var/log/messages 动态查看日志文件尾部: tail -f /var/log/messages 2、安全…...

AI 绘画爆火背后:扩散模型原理及实现
节前,我们星球组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、参加社招和校招面试的同学。 针对算法岗技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备、面试常考点分享等热门话题进行了深入的讨论。 合集&#x…...

详解智慧互联网医院系统源码:开发医院小程序教学
本篇文章,笔者将详细介绍智慧互联网医院系统的源码结构,并提供开发医院小程序的详细教学。 一、智慧互联网医院系统概述 智慧互联网医院系统涵盖了预约挂号、在线咨询、电子病历、药品管理等多个模块。 二、系统源码结构解析 智慧互联网医院系统的源码…...
【技术实操】银河高级服务器操作系统实例分享,数据库日志文件属主不对问题分析
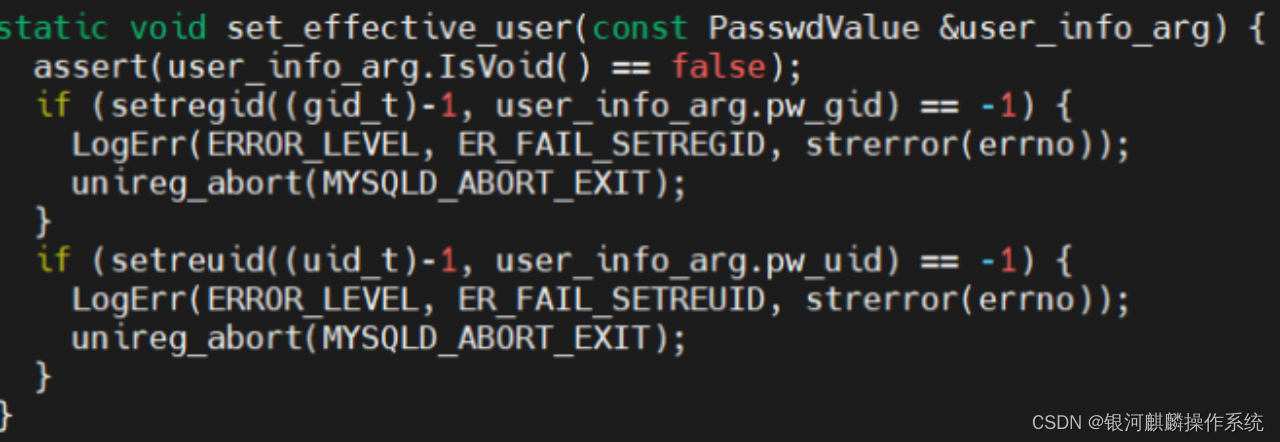
1. 问题现象描述 2023 年 06 月 30 日在迁移数据库过程中,遇到数据库 crash 的缺陷,原因如下:在数据库启动时候生成的一组临时文件中,有 owner 为 root 的文件, 文件权限默认为 640, 当数据库需要使用的时…...

函数的创建和调用
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 提到函数,大家会想到数学函数吧,函数是数学最重要的一个模块,贯穿整个数学学习过程。在Python中,函数…...

数模混合芯片设计中的修调技术是什么?
一、修调目的 数模混合芯片需要修调技术主要是因为以下几个原因: 工艺偏差(Process Variations): 半导体制造过程中存在不可避免的工艺偏差,如晶体管尺寸、阈值电压、电阻和电容值等,这些参数的实际值与…...
MySQL 自定义函数(实验报告)
一、实验名称: 自定义函数 二、实验日期: 2024年 6 月 1 日 三、实验目的: 掌握MySQL自定义函数的创建及调用; 四、实验用的仪器和材料: 硬件:PC电脑一台; 配置:内存&#…...

一次职业院校漏洞挖掘
这个是之前挖掘到的漏洞,目前网站进行重构做了全新的改版,但是这个漏洞特别经典,拿出来进行分享。看到src上面的很多敏感信息泄露,所以自己也想找一个敏感信息泄露,官网如图: 发现在下面有一个数字校园入口…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
