Open3D(C++) OTSU点云二值化
相关文章：
Open3D(C++) OTSU点云二值化
目录 一、算法原理二、代码实现三、结果展示1、原始点云2、二值化本文由CSDN点云侠原创，原文链接。如果你不是在点云侠的博客中看到该文章，那么此处便是不要脸的爬虫与GPT。 一、算法原理 最大类间方差法（Between-class scatter method）是一种用于分割的方法，它通过计算图…...
浔川python社获得全网博主原力月度排名泸州地区第二名！
今日，浔川python社在查看全网博主原力月度排名泸州地区时，一看就震惊啦！ 全网博主原力月度排名泸州地区排名榜单 全网博主原力月度排名泸州地区第二名为：浔川python社。 感谢粉丝们的支持！浔川python社还会继续努力&a…...
第二站：Java——集合框架的深邃海洋（续）
### Java——集合框架的深邃海洋（续） 在我们的Java集合框架探索之旅中，我们已经涉足了基本操作、高级特性，现在让我们深入探讨一些特定场景下的应用和进阶技巧，比如集合的分区操作、分组、并行流的性能考量࿰…...
linux系统下，mysql增加用户
首先，在linux进入mysql mysql -u root -p 然后查看当前用户： select user,host from user; 增加用户语句： CREATE USER 用户名host范围 IDENTIFIED BY 密码;...
)
Java数据结构与算法(最长回文子串中心扩散法)
前言 回文子串是练习数据结构和算法比较好的使用场景，可以同时练习到双指针、动态规划等一些列算法。 实现原理 中心扩散算法实现。这里定义最长回文子串长度的大小为maxLen，起点位置为0. 奇数个数为中心点和偶数个数为中心点分别计算回文长度大小。…...
基于Python网络招聘数据可视化分析系统的设计与实现
基于Python网络招聘数据可视化分析系统的设计与实现 Design and Implementation of Python-based Network Recruitment Data Visualization Analysis System 完整下载链接:基于Python网络招聘数据可视化分析系统的设计与实现 文章目录 基于Python网络招聘数据可视化分析系统的…...
【Linux】Linux工具——gcc/g++
1.使用vim更改信用名单——sudo 我们这里来补充sudo的相关知识——添加信任白名单用户 使用sudo就必须将使用sudo的那个账号添加到信用名单里，而且啊，只有超级管理员才可以添加 信用名单在/etc/sudoers里 我们发现它的权限只是可读啊，所以…...
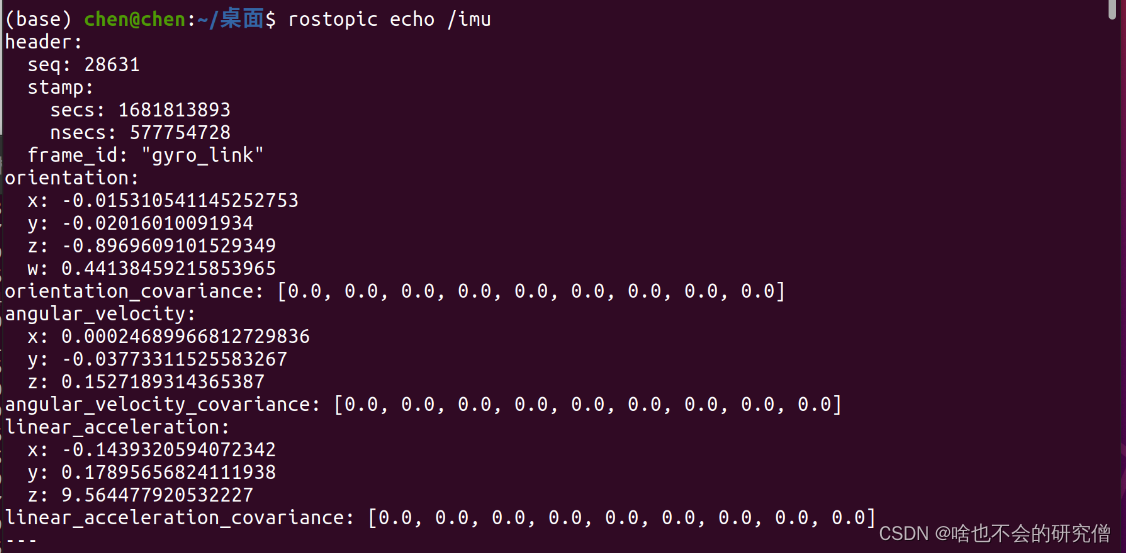
【惯性传感器imu】—— WHEELTEC的惯导模块的imu的驱动安装配置和运行
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言一、IMU驱动安装1. 安装依赖2. 源码的下载3. 编译源码(1) 配置固定串口设备(2) 修改luanch文件(3) 编译 二、启动IMU1. 运行imu2. 查看imu数据 总结 前言 WHEE…...
Linux提权一
#信息收集 当前主机的操作系统 hostnamectl cat /etc/*-release lsb_release -a cat /etc/lsb-release # Debain cat /etc/redhat-release # Redhat cat /etc/centos-release # Centos cat /etc/os-release # Ubuntu cat /etc/issue 当前主机的内核版本 hostnamectl uname -a …...
Vue.js中如何实现以列表首列为表头
前言 一般情况table列表的展示，列头都在第一横行，此方法用于列头在第一列的情况。 效果图 核心代码 <template><div><table class"data-table"><tr v-for"(column, columnIndex) in columns" :key"col…...
如果孙宇晨和贾跃亭能够握手，或许将会上演新的戏码
就在贾跃亭宣布将进行个人IP的商业化不久，便迎来了回应，并且这一次给予贾跃亭回应的，同样是一个颇具争议性的人物——孙宇晨。 根据孙宇晨最新发布的视频显示，他愿意投资贾跃亭「做一个新的个人IP化的公司」，并且将会…...
渲染100为什么是高性价比网渲平台？渲染100邀请码1a12
市面上主流的网渲平台有很多，如渲染100、瑞云、炫云、渲云等，这些平台各有特色和优势，也都声称自己性价比高，以渲染100为例，我们来介绍下它的优势有哪些。 1、渲染100对新用户很友好，注册填邀请码1a12有3…...
Jenkins流水线pipeline--基于上一章的工作流程
1流水线部署 1.流水线文本名Jenkinsfile,将流水线放入gitlab远程仓库代码里面 2pipeline脚本 Jenkinsfile文件内容 pipeline {agent anyenvironment {key"value"}stages {stage("拉取git仓库代码") {steps {deleteDir()checkout scmGit(branches: [[nam…...
比较Rust和Haskel
在比较Rust和Haskell时，我们可以从多个维度来分析它们各自的优势。以下是Rust相对于Haskell的优势，以及Haskell相对于Rust的优势： Rust比Haskell强的方面： 内存安全与并发性： Rust通过独特的所有权系统和借用检查器在…...
RedisTemplate的Long类型使用increment自增报错
问题描述 代码如下 Resourceprivate RedisTemplate<String,String > redisTemplate;redisTemplate.opsForValue().set("testKey", 0L); redisTemplate.opsForValue().increment("testKey");工作里用Long类型存储评论数，在使用increment自…...
【代码随想录训练营】【Day 36】【贪心-3】| Leetcode 1005, 134, 135
【代码随想录训练营】【Day 36】【贪心-3】| Leetcode 1005, 134, 135 需强化知识点 题目 1005. K 次取反后最大化的数组和 贪心：翻转绝对值最小的数思路：将数组按绝对值降序排序后，从左向右遍历数组，如果遇到小于0的数并且还…...
2.7HDR与LDR
一、基本概念 1.基本概念 动态范围（Dynamic Range） 最高亮度 / 最低亮度 HDR High Dynamic RangeLDR Low Dynamic Range HDR与LDR和Tonemapping的对应关系： 我们常用的各种显示器屏幕，由于不同的厂家不同的工艺导致它们的…...
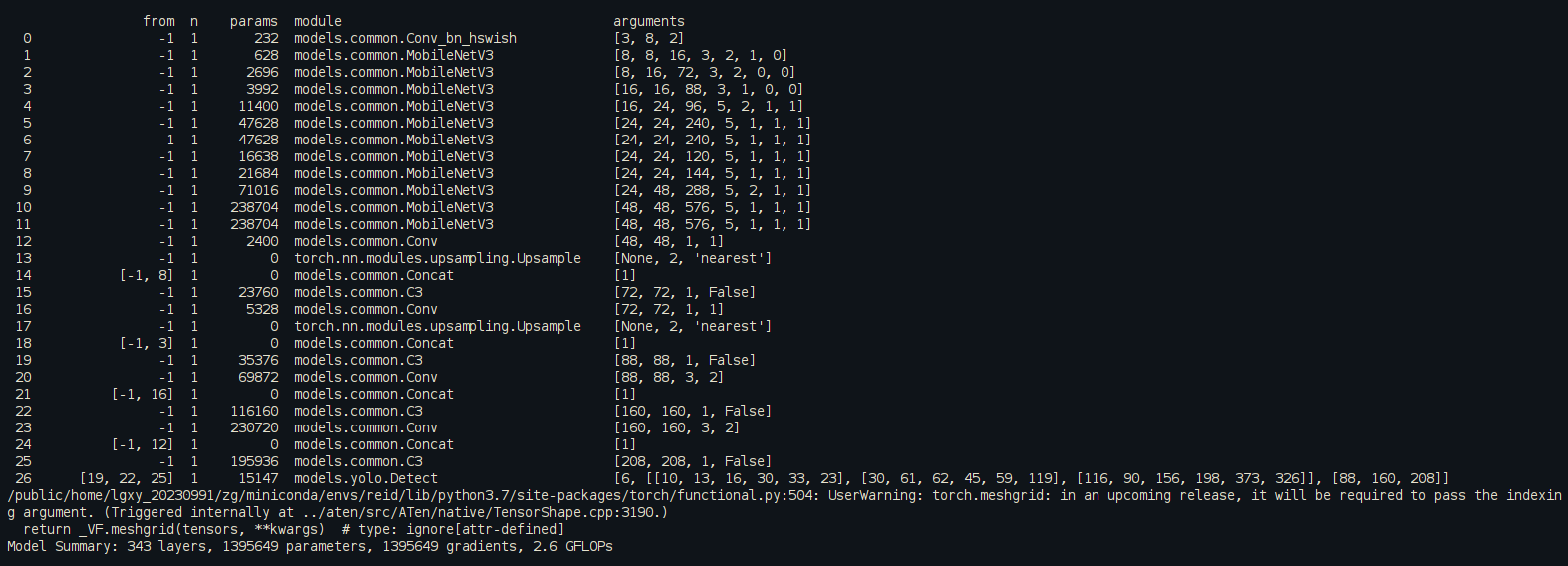
YOLOv5改进（五）-- 轻量化模型MobileNetv3
文章目录 1、MobileNetV3论文2、代码实现2.1、MobileNetV3-small2.2、MobileNetV3-large 3、运行效果4、目标检测系列文章 1、MobileNetV3论文 Searching for MobileNetV3论文 MobileNetV3代码 MobileNetV3 是 Google 提出的一种轻量级神经网络结构，旨在在移动设备上…...
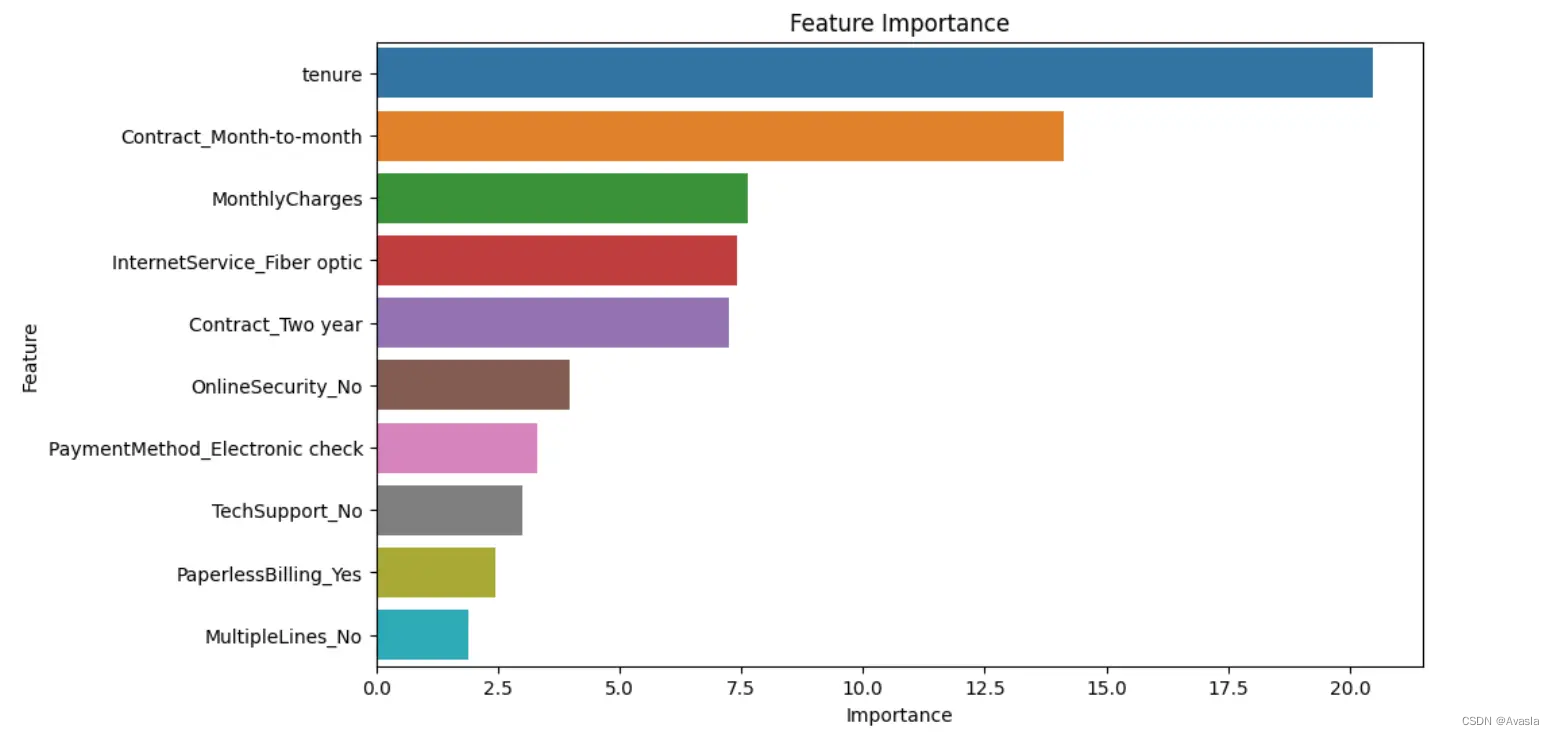
用户流失分析：如何使用Python训练一个用户流失预测模型？
引言 在当今商业环境中，客户流失分析是至关重要的一环。随着市场竞争的加剧，企业需要更加注重保持现有客户，并深入了解他们的离开原因。本文探讨了用户流失分析的核心概念以及如何构建客户流失预测模型的案例。通过分析用户行为数据和交易模式…...
【计算机毕设】基于SpringBoot的社区医院信息平台设计与实现 - 源码免费（私信领取）
免费领取源码 ｜ 项目完整可运行 ｜ v：chengn7890 诚招源码校园代理！ 1. 引言 随着医疗信息化的不断推进，社区医院作为基层医疗机构，需要建立高效、便捷的信息管理平台以提高服务质量和工作效率。基于SpringB…...
脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）
一、数据处理与分析实战 （一）实时滤波与参数调整 基础滤波操作 60Hz 工频滤波：勾选界面右侧 “60Hz” 复选框，可有效抑制电网干扰（适用于北美地区，欧洲用户可调整为 50Hz）。 平滑处理&…...
Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中，拉取视频流只要求udp方式，从2016开始要求新增支持tcp被动和tcp主动两种方式，udp理论上会丢包的，所以实际使用过程可能会出现画面花屏的情况，而tcp肯定不丢包，起码…...
【人工智能】神经网络的优化器optimizer（二）：Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad（Adaptive Gradient Algorithm）是一种自适应学习率的优化算法，由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率，适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时，需结合业务场景设计数据流转链路，重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点： 一、核心对接场景与目标 商品数据同步 场景：将1688商品信息…...
反射获取方法和属性
Java反射获取方法 在Java中，反射（Reflection）是一种强大的机制，允许程序在运行时访问和操作类的内部属性和方法。通过反射，可以动态地创建对象、调用方法、改变属性值，这在很多Java框架中如Spring和Hiberna…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
WEB3全栈开发——面试专业技能点P2智能合约开发（Solidity）
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解，适合用作学习或写简历项目背景说明。 🧠 一、概念简介：Solidity 合约开发 Solidity 是一种专门为 以太坊（Ethereum）平台编写智能合约的高级编…...
EtherNet/IP转DeviceNet协议网关详解
一，设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络，本网关连接到EtherNet/IP总线中做为从站使用，连接到DeviceNet总线中做为从站使用。 在自动…...
深入解析C++中的extern关键字：跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析：跨文件编程的终极指南 📅 更新时间：2025年6月5日 🏷️ 标签：C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么？&…...
Caliper 配置文件解析：config.yaml
Caliper 是一个区块链性能基准测试工具，用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构，并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件，主要包含以下几个部…...