Python | MATLAB | R 心理认知数学图形模型推断
🎯要点
🎯图形模型推断二元过程概率:🖊模型1:确定成功率 θ 的后验分布 | 🖊模型2:确定两个概率差 δ \delta δ 的后验分布 | 🖊模型3:确定底层概率,后验预测 | 🖊模型4:推断概率分布和试验次数
模型1 分布:
θ ∼ Beta ( 1 , 1 ) k ∼ Binomial ( θ , n ) \begin{aligned} & \theta \sim \operatorname{Beta}(1,1) \\ & k \sim \operatorname{Binomial}(\theta, n)\end{aligned} θ∼Beta(1,1)k∼Binomial(θ,n)
模型2 分布:
k 1 ∼ Binomial ( θ 1 , n 1 ) k 2 ∼ Binomial ( θ 2 , n 2 ) θ 1 ∼ Beta ( 1 , 1 ) θ 2 ∼ Beta ( 1 , 1 ) δ ← θ 1 − θ 2 \begin{aligned} k_1 & \sim \operatorname{Binomial}\left(\theta_1, n_1\right) \\ k_2 & \sim \operatorname{Binomial}\left(\theta_2, n_2\right) \\ \theta_1 & \sim \operatorname{Beta}(1,1) \\ \theta_2 & \sim \operatorname{Beta}(1,1) \\ \delta & \leftarrow \theta_1-\theta_2\end{aligned} k1k2θ1θ2δ∼Binomial(θ1,n1)∼Binomial(θ2,n2)∼Beta(1,1)∼Beta(1,1)←θ1−θ2
模型3 分布:
k 1 ∼ Binomial ( θ , n 1 ) k 2 ∼ Binomial ( θ , n 2 ) θ ∼ Beta ( 1 , 1 ) \begin{aligned} k_1 & \sim \operatorname{Binomial}\left(\theta, n_1\right) \\ k_2 & \sim \operatorname{Binomial}\left(\theta, n_2\right) \\ \theta & \sim \operatorname{Beta}(1,1)\end{aligned} k1k2θ∼Binomial(θ,n1)∼Binomial(θ,n2)∼Beta(1,1)
模型4 分布:
k i ∼ Binomial ( θ , n ) θ ∼ Beta ( 1 , 1 ) n ∼ Categorical ( 1 n max , … , 1 n max ⏟ m ) \begin{aligned} k_i & \sim \operatorname{Binomial}(\theta, n) \\ \theta & \sim \operatorname{Beta}(1,1) \\ n & \sim \operatorname{Categorical}(\underbrace{\frac{1}{n_{\max }}, \ldots, \frac{1}{n_{\max }}}_m)\end{aligned} kiθn∼Binomial(θ,n)∼Beta(1,1)∼Categorical(m nmax1,…,nmax1)
🎯图形模型高斯推理:🖊模型5:推断高斯分布生成的数据的平均值和标准差 | 🖊模型6:标准差和观察值添加精度先验,推断高斯平均值 | 🖊模型7:重复测量推断智商
模型5 分布:
μ ∼ Gaussian ( 0 , 0.001 ) σ ∼ Uniform ( 0 , 10 ) x i ∼ Gaussian ( μ , 1 σ 2 ) \begin{aligned} \mu & \sim \operatorname{Gaussian}(0,0.001) \\ \sigma & \sim \operatorname{Uniform}(0,10) \\ x_i & \sim \operatorname{Gaussian}\left(\mu, \frac{1}{\sigma^2}\right)\end{aligned} μσxi∼Gaussian(0,0.001)∼Uniform(0,10)∼Gaussian(μ,σ21)
模型6分布:
μ ∼ Gaussian ( 0 , 0.001 ) λ i ∼ Gamma ( 0.001 , 0.001 ) σ i ← 1 / λ i x i ∼ Gaussian ( μ , λ i ) \begin{aligned} \mu & \sim \operatorname{Gaussian}(0,0.001) \\ \lambda_i & \sim \operatorname{Gamma}(0.001,0.001) \\ \sigma_i & \leftarrow 1 / \sqrt{\lambda_i} \\ x_i & \sim \operatorname{Gaussian}\left(\mu, \lambda_i\right)\end{aligned} μλiσixi∼Gaussian(0,0.001)∼Gamma(0.001,0.001)←1/λi∼Gaussian(μ,λi)
模型7分布:
μ i ∼ Uniform ( 0 , 300 ) σ ∼ Uniform ( 0 , 100 ) x i j ∼ Gaussian ( μ i , 1 σ 2 ) \begin{aligned} \mu_i & \sim \operatorname{Uniform}(0,300) \\ \sigma & \sim \operatorname{Uniform}(0,100) \\ x_{i j} & \sim \operatorname{Gaussian}\left(\mu_i, \frac{1}{\sigma^2}\right)\end{aligned} μiσxij∼Uniform(0,300)∼Uniform(0,100)∼Gaussian(μi,σ21)
🎯数据分析:🖊模型8:计算皮尔逊相关系数
模型8 分布:
μ 1 , μ 2 ∼ Gaussian ( 0 , 0.001 ) σ 1 , σ 2 ∼ InvSqrtGamma ( 0.001 , 0.001 ) r ∼ Uniform ( − 1 , 1 ) x i ∼ MvGaussian ( ( μ 1 , μ 2 ) , [ σ 1 2 r σ 1 σ 2 r σ 1 σ 2 σ 2 2 ] − 1 ) \begin{aligned} \mu_1, \mu_2 & \sim \operatorname{Gaussian}(0,0.001) \\ \sigma_1, \sigma_2 & \sim \operatorname{InvSqrtGamma}(0.001,0.001) \\ r & \sim \operatorname{Uniform}(-1,1) \\ x _i & \sim \operatorname{MvGaussian}\left(\left(\mu_1, \mu_2\right),\left[\begin{array}{cc}\sigma_1^2 & r \sigma_1 \sigma_2 \\ r \sigma_1 \sigma_2 & \sigma_2^2\end{array}\right]^{-1}\right)\end{aligned} μ1,μ2σ1,σ2rxi∼Gaussian(0,0.001)∼InvSqrtGamma(0.001,0.001)∼Uniform(−1,1)∼MvGaussian((μ1,μ2),[σ12rσ1σ2rσ1σ2σ22]−1)
🎯时间和记忆关系 | 🎯心里信号检测 | 🎯外部物理刺激内部心理感觉 | 🎯超感知学 | 🎯语义相关连续回忆 | 🎯尺度不变记忆、感知和学习 | 🎯风险判断和偏好个体心里差异 | 🎯多维心理刺激个体相似性
🍇Python后验分布采样计算
贝叶斯计算由一系列方法组成,这些方法可以帮助我们从几乎所有后验分布中采样点,从中我们可以对感兴趣的参数进行点估计。
💦方法一
让我们从一个例子开始,如果我们想从后验分布 f(x) 中绘制点,它具有以下函数形式:
f ( x ) = x 1.7 ( 1 − x 1 + x ) 5.3 f(x)=x^{1.7}\left(\frac{1-x}{1+x}\right)^{5.3} f(x)=x1.7(1+x1−x)5.3
我们称这个 f(x) 为目标分布/密度,然后我们提出一个更简单的分布(候选分布),我们可以从中采样点。我们使用均匀分布 g(x),希望当将 g(x) 与常数 M 相乘时,Mg(x) 可以包裹 f(x)。此时,M 很容易被选为 f(x) 的最大值。
现在我们首先从另一个均匀分布 Uniform(0,1) 中独立采样,我们将采样点表示为 u。我们还从候选分布 g(x) 中采样,并将采样点表示为 y。我们测试采样点 u 是否符合以下标准:
u ≤ 1 M f ( y ) g ( y ) u \leq \frac{1}{M} \frac{f(y)}{g(y)} u≤M1g(y)f(y)
如果符合,我们将 y 视为目标分布的样本,否则,我们拒绝 y。乍一看,这一步可能很难理解。其背后的想法是,如果有一个区域,比如 [0.2,0.3],其中目标密度 f(x) 的密度非常高,那么该区域内的 f(y)/M*g(y) 也会很高,可能接近 1。由于 u 是从标准均匀分布中随机抽取的(u 只是用来控制是拒绝还是接受 y),这个指标更有可能为真,从而导致接受采样的 y。
💦代码
x = np.linspace(0,1,1000)
f_x = x**1.7*((1-x)/(1+x))**5.3
M = f_x.max()
def f(x):return x**1.7*((1-x)/(1+x))**5.3
def g(x):return uniform.pdf(x,loc=0,scale=1)n = 2500
u = uniform.rvs(loc=0,scale=1,size=n,random_state=1)
y = uniform.rvs(loc=0,scale=1,size=n,random_state=2)
f_y = f(y)
g_y = g(y)
acc_or_rej = u <= f_y / (M * g_y)
accepted_y = y[acc_or_rej]
sns.histplot(accepted_y)
估计的目标分布可以绘制如下(图略)。
💦方法二:
蒙特卡罗方法代表了一类广泛的算法,这些算法依赖于重复随机抽样来估计所需的数量。该数量可能是圆周率值,也可能是陌生函数形式的积分。蒙特卡罗最经典的例子是估计圆周率的值,我们首先从两个标准均匀分布中随机抽取 x 和 y,并询问 x 2 + y 2 x^2+y^2 x2+y2 是否 < 1,如果答案为真,则将计数器加 1。在随机抽样结束时,我们可以计算计数器与总迭代次数的比率(如果使用正方形和内切圆的面积公式,则应为 pi/4)。
马尔可夫链是一个随机过程,其中当前值仅取决于其直接前一个值。我非常喜欢的一个简单例子是天气预报,如果我们假设一天的天气有三种可能的状态(晴天、多云、下雨),我们有一个初始分布,其中 p(晴天)=0.6、p(多云)=0.3 和 p(下雨)=0.1,现在给定一个转换核 K,它是一个矩阵
( 晴天 阴天 雨天 晴天 0.5 0.3 0.2 阴天 0.3 0.5 0.2 雨天 0.2 0.4 0.4 ) \left(\begin{array}{cccc} & \text { 晴天 } & \text { 阴天 } & \text { 雨天 } \\ \text { 晴天 } & 0.5 & 0.3 & 0.2 \\ \text { 阴天 } & 0.3 & 0.5 & 0.2 \\ \text { 雨天 } & 0.2 & 0.4 & 0.4 \end{array}\right) 晴天 阴天 雨天 晴天 0.50.30.2 阴天 0.30.50.4 雨天 0.20.20.4
我们能够使用初始分布和转换内核导出任意一天的状态分布。当我们继续这样做时,如果状态分布保持不变,它就会达到平稳分布。
虽然马尔可夫链的离散场景更容易理解,但我们最终需要将其推广到状态空间无限的连续情况,这意味着我们将拥有无限多个状态,而不是只有三个状态(晴天、多云、下雨)。所以我们需要使用分布来表示每个时间点的状态分布。例如,如果我们说状态的初始分布遵循 Normal(0,3),那么转移概率也应该是 p(x_n+1|x_n) = K(x_n+1|x_n) = Normal(x_n,0.1) 的分布,并且所有上述属性与离散场景保持一致。
现在我们要从目标密度 f(x) 中采样:
f ( x ) = 2 x 2 ( 1 − x ) 8 cos ( 4 π x ) 2 f(x)=2 x^2(1-x)^8 \cos (4 \pi x)^2 f(x)=2x2(1−x)8cos(4πx)2
假设我们正在创建一个马尔可夫链,其中转换内核 q(x,y) 为(其中 x 是当前时间点,y 是最后一个时间点):
q ( x , y ) = Normal ( y , 0.1 ) q(x, y)=\operatorname{Normal}(y, 0.1) q(x,y)=Normal(y,0.1)
Metropolis-Hasting (MH) 算法首先初始化向量 x 的第一个值(假设我们将使用 MCMC 采样 n=10,000 个 x 值)x[0] 。然后在每次迭代中,我们首先使用转换内核生成一个 x_cand,并且我们需要计算接受率 alpha 来决定下一个 x 是采用 x_cand 还是仅采用最后一个 x 值。接受率如下所示:
α ( x cand ∣ x i − 1 ) = min { 1 , q ( x i − 1 ∣ x cand ) f ( x cand ) q ( x cand ∣ x i − 1 ) f ( x i − 1 ) } \alpha\left(x_{\text {cand }} \mid x_{i-1}\right)=\min \left\{1, \frac{q\left(x_{i-1} \mid x_{\text {cand }}\right) f\left(x_{\text {cand }}\right)}{q\left(x_{\text {cand }} \mid x_{i-1}\right) f\left(x_{i-1}\right)}\right\} α(xcand ∣xi−1)=min{1,q(xcand ∣xi−1)f(xi−1)q(xi−1∣xcand )f(xcand )}
代码如下:
def f(x):import mathreturn 2*x**2*(1-x)**8*math.cos(4*math.pi*x)**2
def q(x,y):return norm.pdf(x,loc=y,scale=0.1)n = 10000
x = np.zeros(n)
x[0] = norm.rvs(loc=0,scale=0.1,size=1)[0]
for i in range(n-1):while True:x_cand = norm.rvs(loc=x[i],scale=0.1,size=1)[0]if x_cand >= 0 and x_cand <= 1:breakif x_cand >= 0 and x_cand <= 1:rho = (q(x[i],x_cand)/q(x_cand,x[i]))*(f(x_cand)/f(x[i]))alpha = min(1,rho)u = uniform.rvs(loc=0,scale=1,size=1)[0]if u < alpha:x[i+1] = x_candelse:x[i+1] = x[i]
sns.histplot(x)
fig,ax = plt.subplots()
ax.plot(np.arange(10000),x)
💦分层贝叶斯
nruns = 10000
K = 100
n = 1000
y = np.zeros(K,n)
lambda_est = np.zeros(K,nruns)
sigma_est = np.zeros(nruns)
mu_est = np.zeros(nruns)
tau_est = np.zeros(nruns)for i in range(K):loc = uniform.rvs(loc=0,scale=10,size=1)[0]scale = uniform.rvs(loc=0,scale=0.1,size=1)[0]lambda_est[i,0] = norm.rvs(loc=loc,scale=scale,size=1)[0]
sigma_est[0] = uniform.rvs(loc=0,scale=0.1,size=1)[0]
mu_est[0] = norm.rvs(loc=uniform.rvs(loc=0,scale=10,size=1)[0],scale=1,size=1)[0]
tau_est[0] = uniform.rvs(loc=0,scale=0.1,size=1)[0]for runs in range(1,n_runs-1,1):for i in range(1,K-1):mean = i/math.sqrt(1/tau_est[runs-1]) + n/sigma_est[runs-1]std = (mean^2)*(mu_est[runs-1]/(tau_est[runs-1])+y[i,:].mean()*n/sigma_est[runs-1])lambda_est[i,runs] = norm.rvs(loc=mean,scale=std,size=1)[0]sigma_sum_term = 0for i in range(K):for j in range(n):sigma_sum_term += (y[i,j]-lambda_est[i,runs])**2sigma_est[runs] = invgamma(loc=K*n/2,scale=sigma_sum_term/2)tau_sum_term = 0for i in range(K):tau_sum_term += (lambda_est[i,runs]-mu_est[runs-1])**2tau_est[runs] = invgamma(loc=K/2,scale=tau_sum_term/2)mu_est[runs] = norm.rvs(loc=lambda_est[:,runs-1].mean(),scale=math.sqrt(tau_est[runs]/2))
👉参阅:亚图跨际
相关文章:

Python | MATLAB | R 心理认知数学图形模型推断
🎯要点 🎯图形模型推断二元过程概率:🖊模型1:确定成功率 θ 的后验分布 | 🖊模型2:确定两个概率差 δ \delta δ 的后验分布 | 🖊模型3:确定底层概率,后验预…...

Linux系统tab键无法补齐命令-已解决
在CentOS中,按下tab键就可以自动补全,但是在最小化安装时,没有安装自动补全的包,需要安装一个包才能解决 bash-completion 1.检查是否安装tab补齐软件包(如果是最小化安装,默认没有) rpm -q ba…...
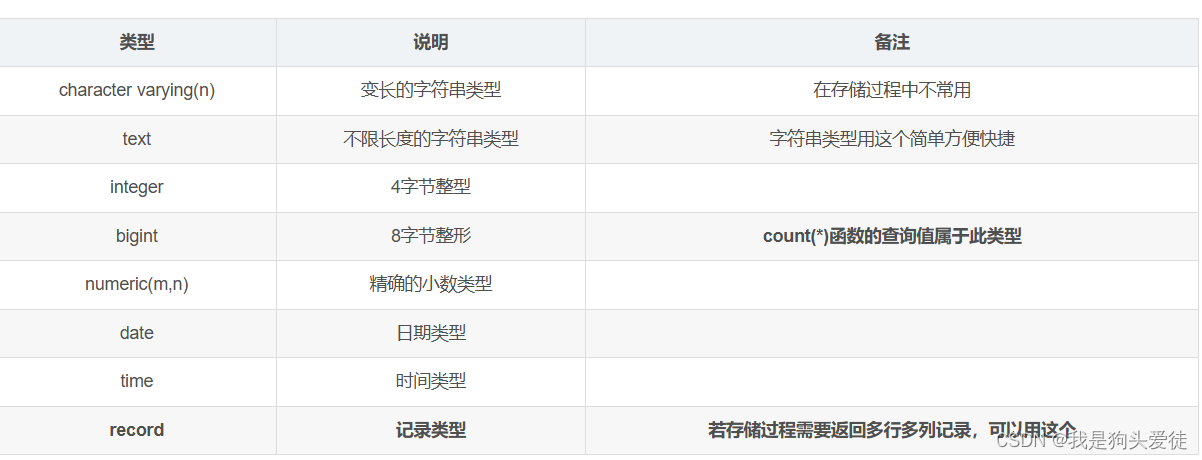
数据库之函数、存储过程
函数、存储过程 1.函数 函数,常用于对一个或多个输入参数进行操作,主要目的是返回一个结果值,就是一种方法,在postgre里存放的位置叫function,比如创建一个计算长方面积的函数。 举例:建立一个计算长方形…...
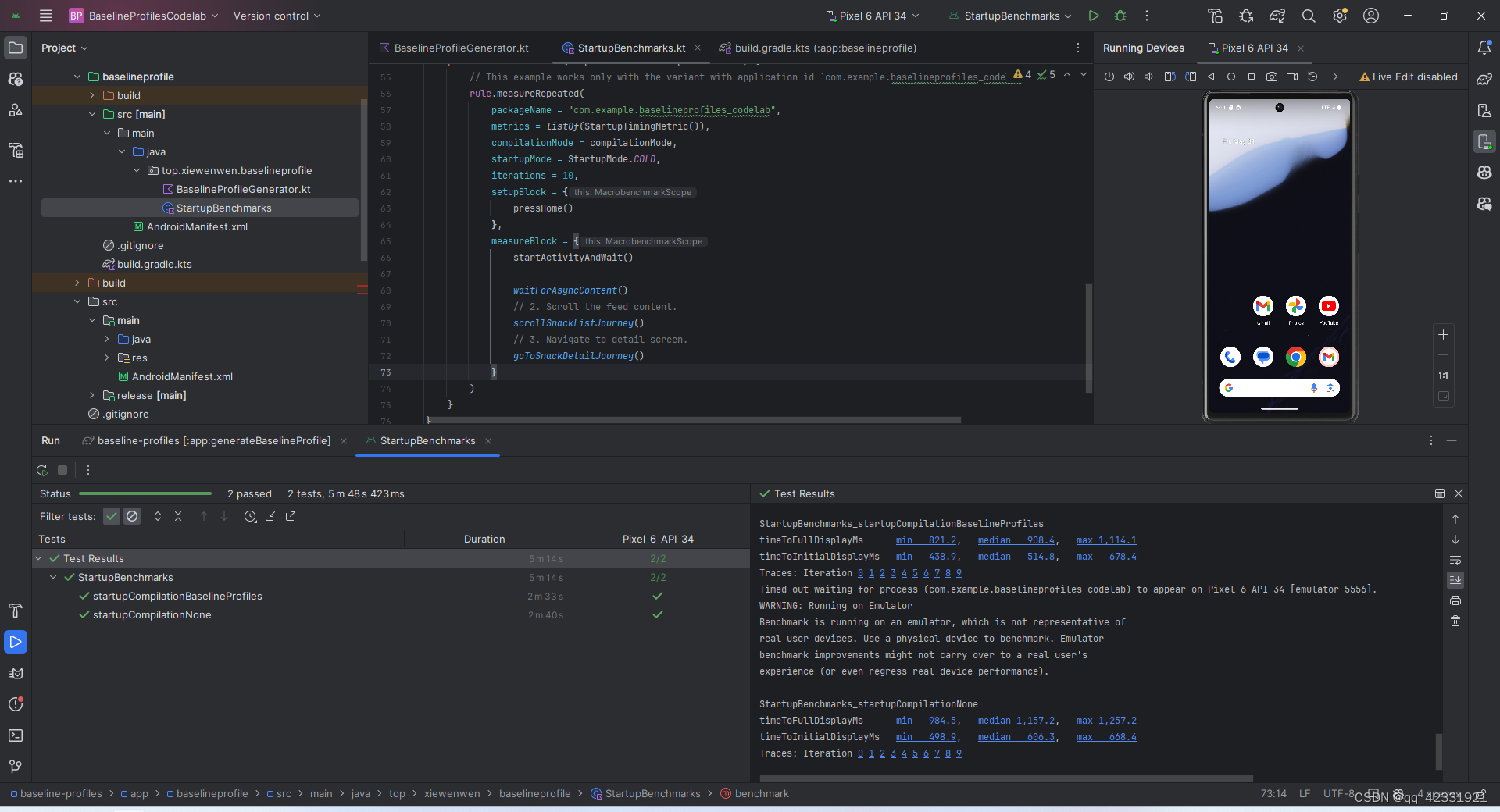
安卓启动 性能提升 20-30% ,基准配置 入门教程
1.先从官方下载demohttps://github.com/android/codelab-android-performance/archive/refs/heads/main.zip 2.先用Android studio打开里面的baseline-profiles项目 3.运行一遍app,这里建议用模拟器,(Pixel 6 API 34)设备运行&a…...

Linux C/C++目录和文件的更多操作
1.access()库函数 用于判断当前用户对目录或文件的存取权限 #include<unistd.h>int accsee(const char *pathname,int mode);参数说明: pathname //目录或文件名 mode //需要判断的存取权限,在<unistd.h>预定义如下#define R_OK 4 //读权…...

如何高效地向Redis 6插入亿级别的数据
如何高效地向Redis插入亿级别的数据 背景不可用的方案可用方案:利用管道插入其他命令:参考: 背景 上一条记录;80G的存储;10几个文件,如何快速导入是一个大问题,也是一个很棘手的问题;如下将给出…...

中国历年肥料进口数量统计报告
数据来源于国家统计局,为1991年到2021年我国每年肥料进口数量统计。 2021年,我国进口肥料909万吨,比上年减少151万吨。 数据统计单位为:万吨 数据说明: 数据来源于国家统计局,为海关进出口统计数 我国肥料…...
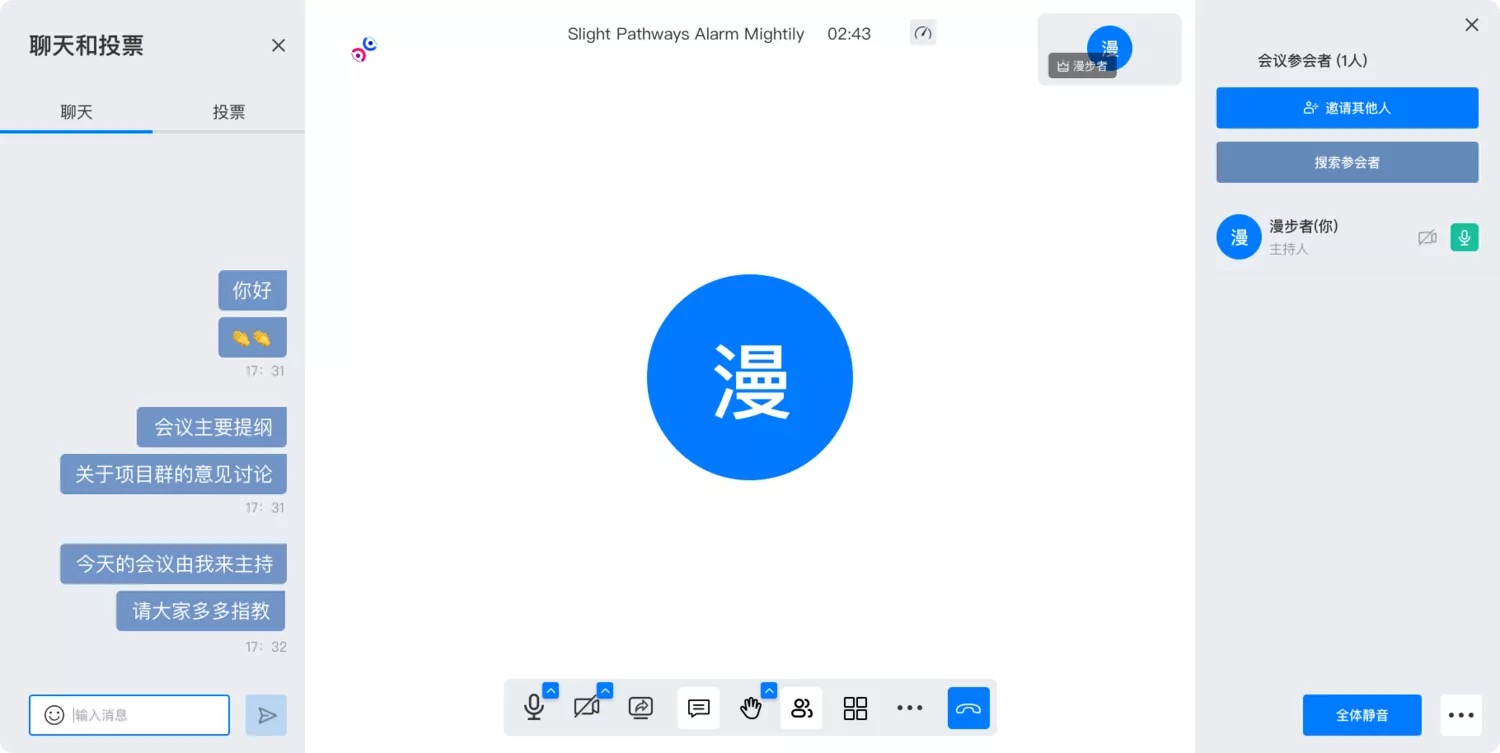
即时通讯视频会议平台,WorkPlus本地化部署解决方案
随着现代科技的快速发展,传统的会议方式已经不再满足企业和组织的需求。即时通讯视频会议以其便利性和高效性,成为了现代企业沟通和协作的重要工具。通过即时通讯视频会议,企业可以实现无时差的交流和远程协作,增强团队合作和提高…...

Java的数据库编程-----JDBC
目录 一.JDBC概念&使用条件: 二.mysql-connector驱动包的下载与导入: 三.JDBC编程: 使用JDBC编程的主要五个步骤: 完整流程1(更新update): 完整流程2(查询query): 一.JDB…...
如何获取SSL证书,消除网站不安全警告
获取SSL证书通常涉及以下几个步骤: 选择证书颁发机构(CA): 你需要从受信任的SSL证书颁发机构中选择一个,比如DigiCert、GlobalSign、JoySSL等。部分云服务商如阿里云、腾讯云也提供免费或付费的SSL证书服务。 生成证…...

Unity动画系统介绍
Unity动画系统介绍 Animator组件: 这是Unity中用于控制动画状态的组件,它与Animator Controller一起工作,可以基于游戏逻辑来切换不同的动画状态。 Animator Controller: 这是一个用于管理动画状态机的组件,它允许…...

Three.js-实现加载图片并旋转
1.实现效果 2. 实现步骤 2.1创建场景 const scene new THREE.Scene(); 2.2添加相机 说明: fov(视场角):视场角决定了相机的视野范围,即相机可以看到的角度范围。较大的视场角表示更广阔的视野,但可能…...

ACM实训第25天
第四套 第一道(修改) #include<stdio.h> #include<string.h> int cnt[10]; void count_digits(int n,int* cnt){for(int i1;i<n;i){int numi;while(num){cnt[num%10];num/10;}} } int main(){int t;scanf("%d\n",&t);whi…...

GraphQL(2):使用express和GraphQL编写helloworld
1 安装express、graphql以及express-graphql 在项目的目录下运行一下命令。 npm init -y npm install express graphql express-graphql -S 2 新建helloworld.js 代码如下: const express require(express); const {buildSchema} require(graphql); const grap…...

Vue中的计算属性和侦听器:提升响应式编程的艺术
引言 Vue.js是一个用于构建用户界面的渐进式框架,它的核心特性之一是响应式编程。Vue通过数据绑定和响应式系统,使得开发者能够以声明式的方式处理数据变化。在Vue中,计算属性(Computed Properties)和侦听器ÿ…...

JavaScript倍速播放视频
F12打开开发者工具,打开控制台,输入这行代码,视频即可加速播放, 可以调整倍速(2,4,8,16) document. getElementsByTagName("video")[0]. playbackRate16...

ER图介绍
在数据库设计和建模中,实体-关系图(Entity-Relationship Diagram,简称ER图)是一个至关重要的工具。ER图通过图形化的方式描述了现实世界中的实体(Entity)及其之间的关系(Relationship࿰…...

Oracle通过datax迁移线上表到历史库
历史数据迁移 线上库数据增长迅速,需要定期清理历史数据,因为异地灾备,但是带宽很小,不能使用数据泵直接往历史库导数,会导致本地机房到灾备机房的带宽被占满,调研过flink、golden gate、datax,…...
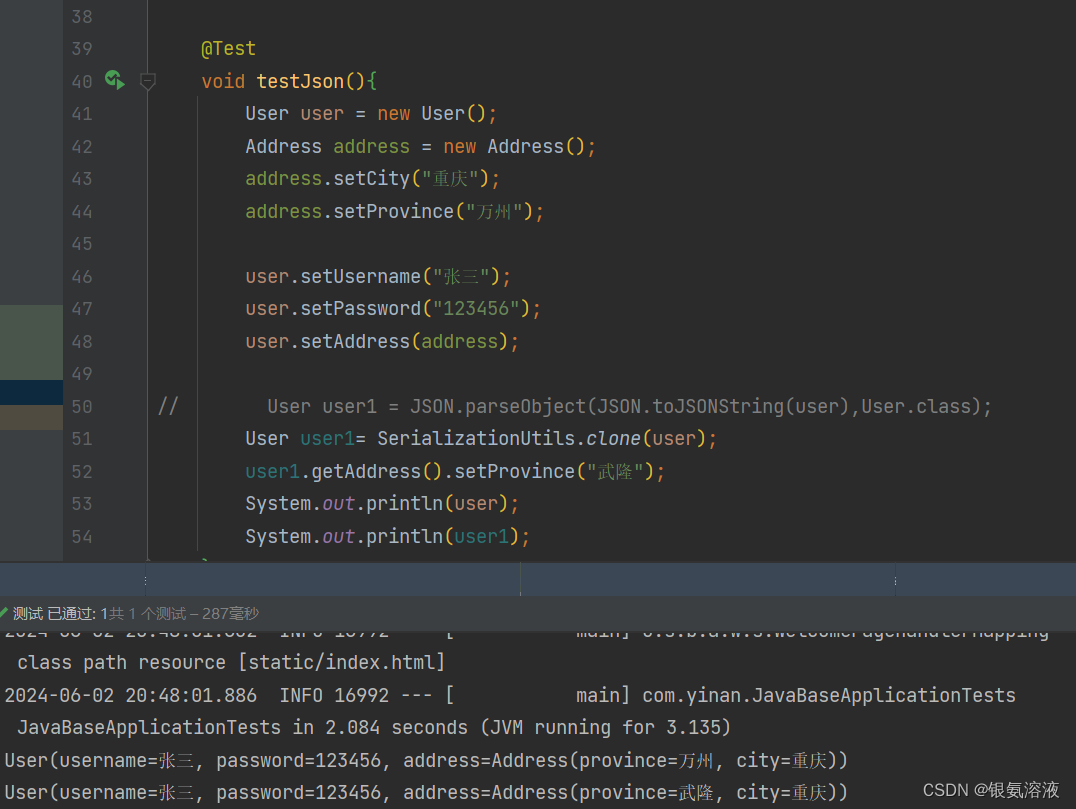
java基础-深拷贝和浅拷贝
java中有一个概念叫深拷贝和浅拷贝,那这两个是什么意思呢?其实你可以对比一下c中的传值和传引用的问题。 深拷贝 即两个相同的对象地址不同,比如对象A通过拷贝出来对象B,在对B对象进行操作时不会影响到A对象的内容。 浅拷贝 和…...
Java数组操作
数组拓展 1.1 数组拷贝 需求:定义一个方法arraycopy, 从指定源数组中从指定的位置开始复制指定数量的元素到目标数组的指定位置。 1.2. 排序操作 需求:完成对int[] arr new int[]{2,9,6,7,4,1}数组元素的升序排序操作. 1.2.1.冒泡排序 对未排序的各元素…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
