算法(十三)回溯算法---N皇后问题
文章目录
- 算法概念
- 经典例子 - N皇后问题
- 什么是N皇后问题?
- 实现思路
算法概念
- 回溯算法是类似枚举的深度优先搜索尝试过程,主要是再搜索尝试中寻找问题的解,当发生不满足求解条件时,就会”回溯“返回(也就是递归返回),尝试别的路径求解。
经典例子 - N皇后问题
什么是N皇后问题?
N皇后问题研究的是:如何将n个皇后放在n * n的棋盘上,并且使皇后彼此之间不能相遇,也就是一个皇后的上下左右、以及斜着对角线上都不能有另外一个皇后,也就是一个皇后在 ”米“ 的视线中不能遇到另外一个皇后。
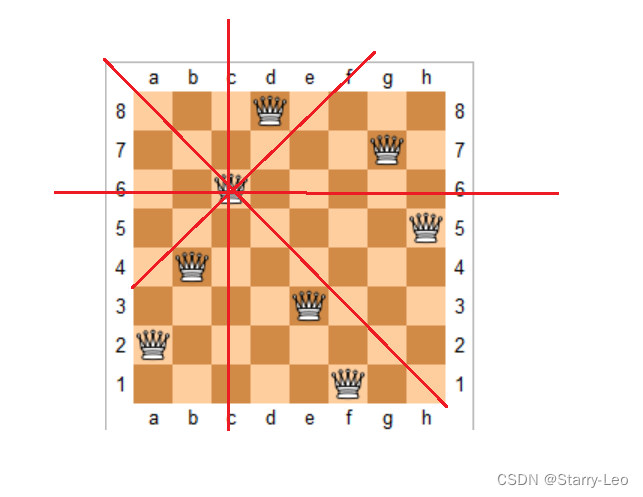
实现思路
如上图,我们可以把这个问题划分成8个阶段,依次将8个棋子放到第一行、第二行…第八行。在放置的过程中,我们不停的检查当前的方法是否满足要求。如果满足,继续下一行放置,如果不满足,就再换一种方法,继续尝试。
实现代码:
package com.xxliao.algorithms.backtrack;/*** @author xxliao* @description: N皇后问题 求解* @date 2024/6/1 0:14*/
public class NQueens {public static void main(String[] args) {NQueens queens=new NQueens();queens.setQueens(0);queens.printQueens();}// 皇后数量static int queens_count = 8;// 定义数组来存在皇后,索引表示行,值表示皇后存在改行的那一列中int[] array = new int[queens_count];/*** @description 根据行号,设置该行的皇后位置* @author xxliao* @date 2024/6/1 0:17*/public void setQueens(int row) {if(row == queens_count) {// 递归结束条件return;}// 尝试每一列放置,如果没有合适的,就返回上一层for(int column = 0; column <queens_count; column++) {if(isOk(row,column)) {// 符合条件,放置array[row] = column;// 然后设置下一行setQueens(++row);}}}/*** @description 判断改行该列是否 符合条件* @author xxliao* @date 2024/6/1 0:23*/private boolean isOk(int row, int column) {// 定义左上角、右上角 列索引标记int leftup = column - 1;int rightup = column + 1;// 然后从当前行逐行向上遍历,看当前row、column是否满足条件for(int i = row-1; i >= 0; i--) {if(array[i] == column){// 如果该位置已经有了皇后了,不满足return false;}if(leftup >=0 && array[i] == leftup) {//左上对角线存在queen,第一次执行是当前行,肯定不满足条件,i--,leftup--之后就是当前点的左上角位置return false;}if(rightup < queens_count && array[i] == rightup) {//右下对角线存在queen,同上理由return false;}leftup--;rightup++;}return true;}/*** @description 打印N皇后棋盘* @author xxliao* @date 2024/6/1 0:34*/private void printQueens() {for (int i = 0; i < queens_count; i++) {for (int j = 0; j < queens_count; j++) {if (array[i] == j) {System.out.print("Q| ");}else {System.out.print("*| ");}}System.out.println();}System.out.println("-----------------------");}
}
演示结果:

相关文章:

算法(十三)回溯算法---N皇后问题
文章目录 算法概念经典例子 - N皇后问题什么是N皇后问题?实现思路 算法概念 回溯算法是类似枚举的深度优先搜索尝试过程,主要是再搜索尝试中寻找问题的解,当发生不满足求解条件时,就会”回溯“返回(也就是递归返回&am…...
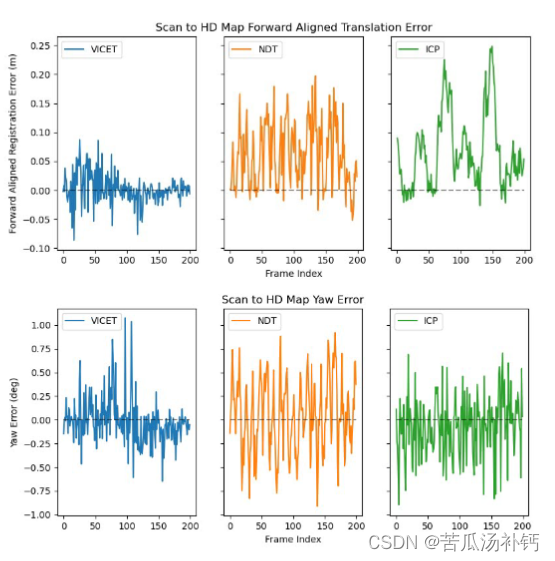
论文阅读:Correcting Motion Distortion for LIDAR HD-Map Localization
目录 概要 Motivation 整体架构流程 技术细节 小结 论文地址:http://arxiv.org/pdf/2308.13694.pdf 代码地址:https://github.com/mcdermatt/VICET 概要 激光雷达的畸变矫正是一个非常重要的工作。由于扫描式激光雷达传感器需要有限的时间来创建…...
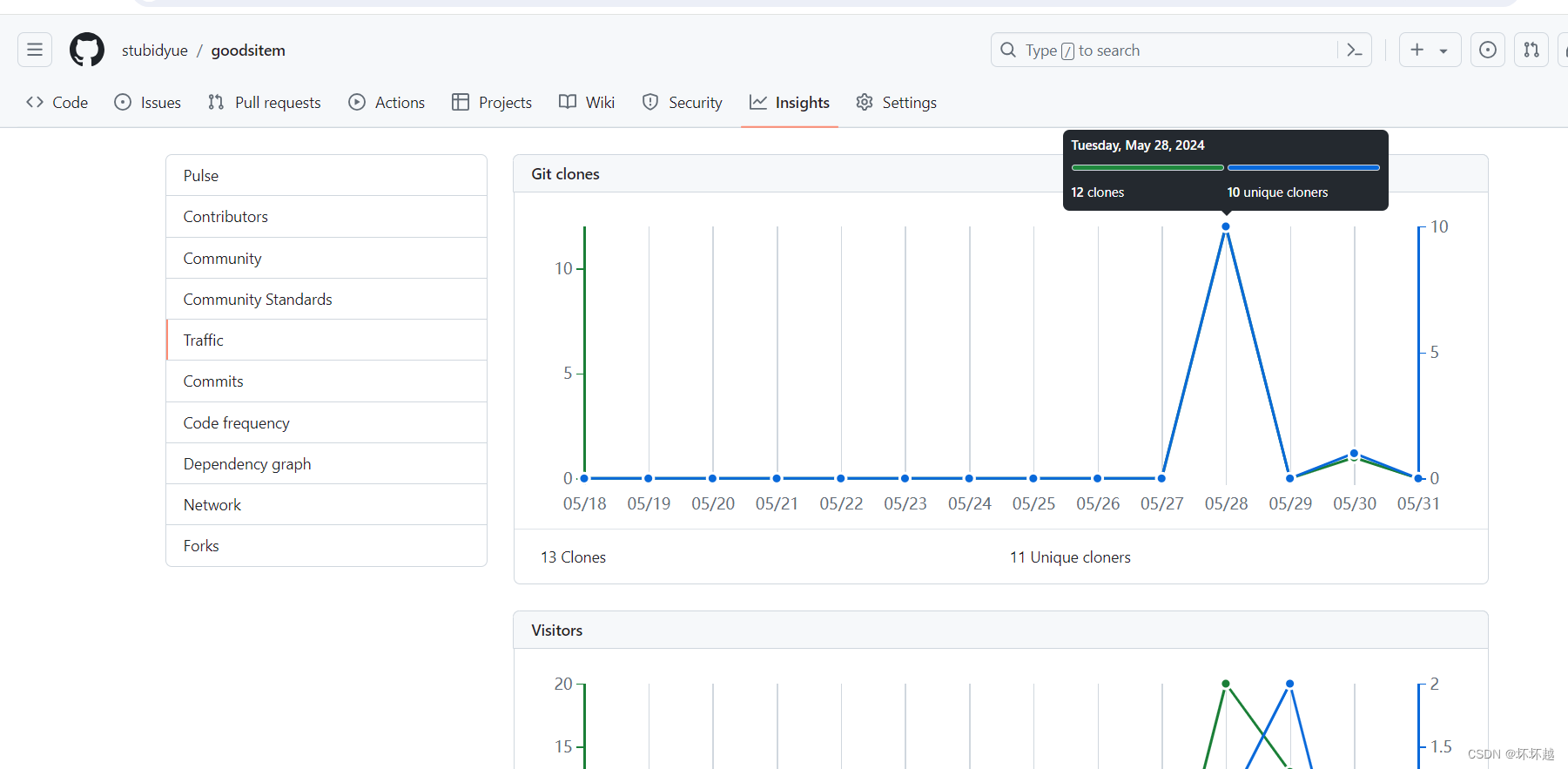
Git操作笔记
学git已经好多次了。但是还是会忘记很多的东西,一些常用的操作命令和遇到的bug以后在这边记录汇总下 一.github图片展示 图片挂载,我是创建了一个库专门存图片,然后在github的md中用专用命令展示图片,这样你的md就不会全是文字那…...

使用Python进行数据分析的基本步骤
简介: 在当今的数据驱动世界中,数据分析已成为各行各业不可或缺的一部分。Python作为一种强大的编程语言,提供了丰富的库和工具,使得数据分析变得简单易行。本文将带你了解使用Python进行数据分析的基本步骤。 一、数据获取 从外…...
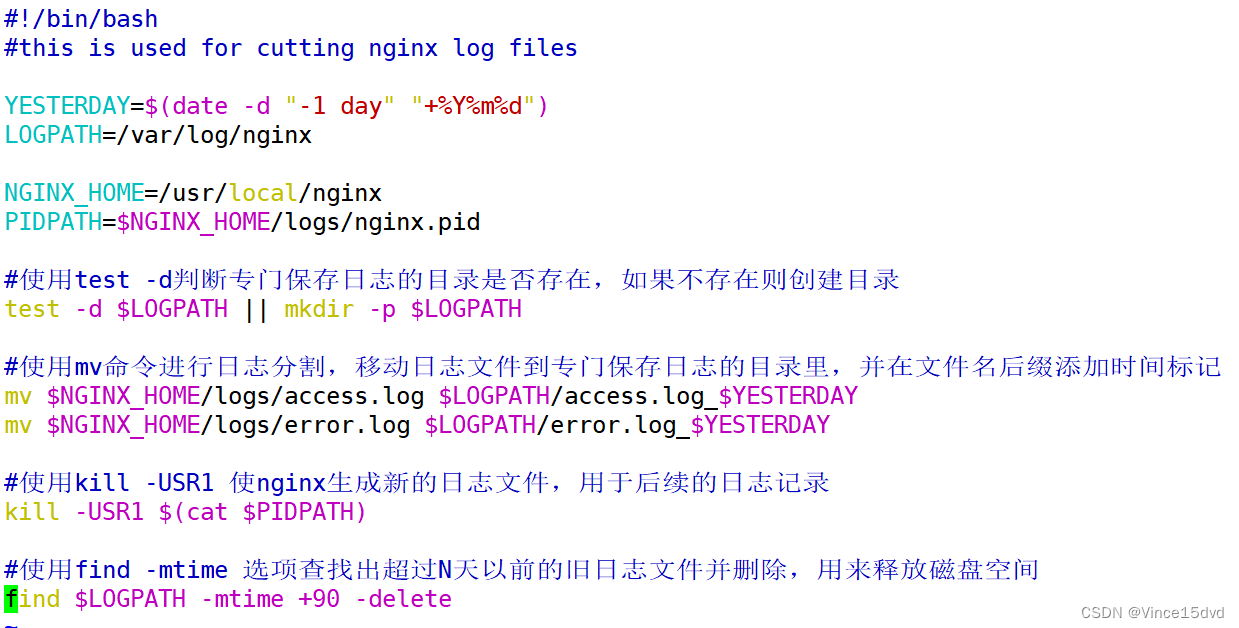
NGINX优化
NGINX优化分为两个方面: 一. nginx应用配置文件的优化: 1.nginx的性能优化: 全局块: 设置工作进程数: work_processes #设置工作进程数 设置工作进程连接数:work_rilmit_nofile #设置每个worker进程最大可…...

【LeetCode刷题】二分查找:山脉数组的峰顶索引、寻找峰值
【LeetCode刷题】Day 13 题目1:852.山脉数组的峰顶索引思路分析:思路1:暴力枚举O(N)思路2:二分查找O(logN) 题目2:162.寻找峰值思路分析:思路1:二分查找O(logN) 题目1:852.山脉数组的…...

《Python学习》-- 实操篇一
一、文件操作 1. 1 读取文本文件 # 文件操作模式 # r (默认) - 只读模式。文件必须存在,否则会抛出FileNotFoundError。在这种模式下,你只能读取文件内容,不能写入或追加。 # w - 写入模式。如果文件存在,内容会被清空ÿ…...
 —— List/Queue类)
C# 集合(二) —— List/Queue类
总目录 C# 语法总目录 集合二 List/Queue 1. List2. Queue 1. List List有ArrayList和LinkedList ArrayList 类似数组,查找快,插入删除慢(相对)LinkedList 类似双向链表,查找慢(相对),插入删除快 //ArrayList //ArrayList Arr…...

【TB作品】MSP430 G2553 单片机口袋板,读取单片机P1.4电压显示,ADC
功能 读取P1.4电压,显示到口袋板显示屏,电压越高亮灯越多。 部分程序 while (1){ADC10CTL0 | ENC ADC10SC; // Sampling and conversion startLPM0;adcvalue ADC10MEM; //原始数据 0到1023adtest (float) adcvalue / 1024.…...

知乎x-zse-96、x-zse-81
声明 本文章中所有内容仅供学习交流使用,不用于其他任何目的,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关!wx a15018601872 本文章未…...

【Linux】Linux工具——yum,vim
1.Linux 软件包管理器——yum Linux安装软件: 源代码安装(不建议)rpm安装(类似Linux安装包,版本可能不兼容,不推荐,容易报错)yum安装(解决了安装源,安装版本&…...
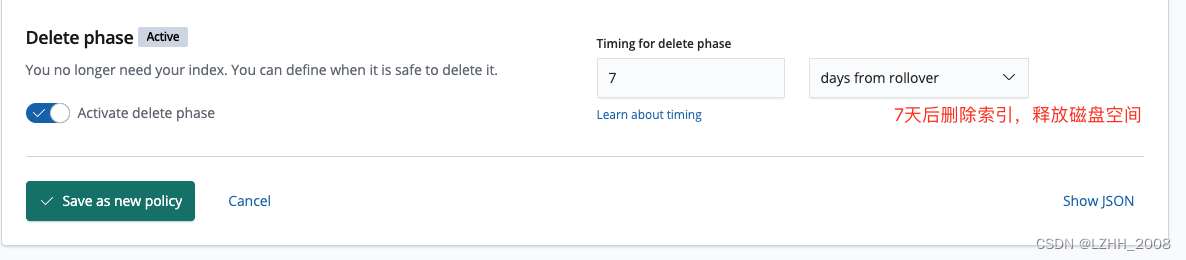
ES 生命周期管理
一 .概念 ILM定义了四个生命周期阶段:Hot:正在积极地更新和查询索引。Warm:不再更新索引,但仍在查询。cold:不再更新索引,很少查询。信息仍然需要可搜索,但是如果这些查询速度较慢也可以。Dele…...

【JavaScript脚本宇宙】揭秘HTTP请求库:深入理解它们的特性与应用
深度揭秘:六大HTTP请求库的比较与应用 前言 在这篇文章中,我们将探讨六种主要的HTTP请求库。这些库为处理网络请求提供了不同的工具和功能,包括Axios、Fetch API、Request、SuperAgent、Got和Node-fetch。通过本文,你将对每个库…...
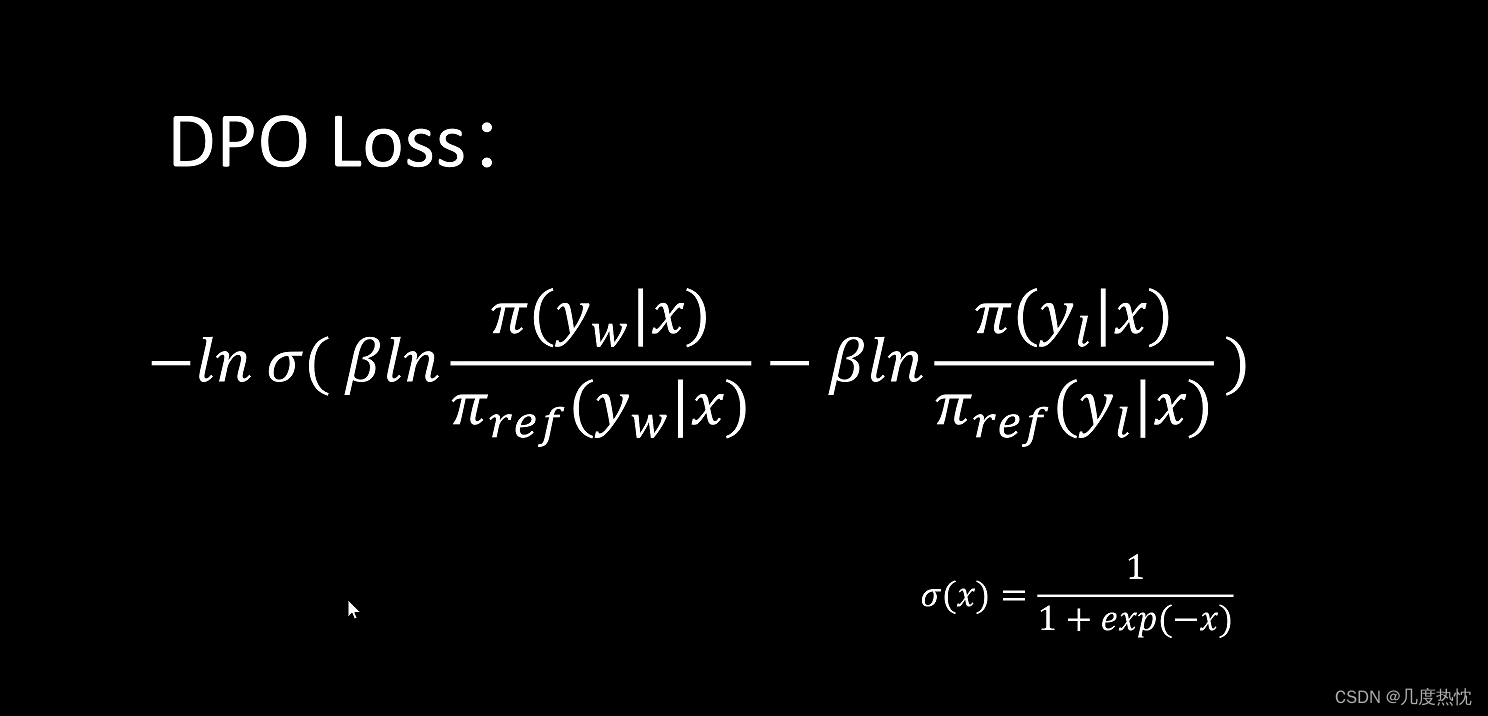
【强化学习】DPO(Direct Preference Optimization)算法学习笔记
【强化学习】DPO(Direct Preference Optimization)算法学习笔记 RLHF与DPO的关系KL散度Bradley-Terry模型DPO算法流程参考文献 RLHF与DPO的关系 DPO(Direct Preference Optimization)和RLHF(Reinforcement Learning f…...

vue3 todolist 简单例子
vue3 简单的TodList 地址: https://gitee.com/cheng_yong_xu/vue3-composition-api-todo-app-my 效果 step-1 初始化项项目 我们不采用vue cli 搭建项目 直接将上图文件夹,复制到vscode编辑器,清空App.vue的内容 安装包 # 安装包 npm…...

Linux项目编程必备武器!
本文目录 一、更换源服务器二、下载man开发手册(一般都自带,没有的话使用下面方法下载) 一、更换源服务器 我们使用apt-get等下载命令下载的软件都是从源服务器上获取的,有些软件包在某个服务器上存在,而另一个服务器不存在。所以我们可以添加…...

AndroidStudio编译很慢问题解决
如果gradle同步、编译下载很慢,可以换一下仓库阿里云镜像 repositories {maven { url https://maven.aliyun.com/repository/google } maven { url https://maven.aliyun.com/repository/jcenter } maven { url https://maven.aliyun.com/repository/public } goog…...
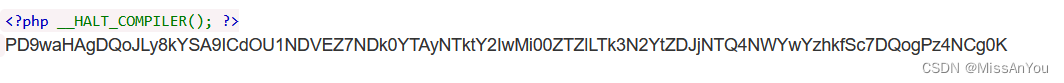
PHAR反序列化
PHAR PHAR(PHP Archive)文件是一种归档文件格式,phar文件本质上是一种压缩文件,会以序列化的形式存储用户自定义的meta-data。当受影响的文件操作函数调用phar文件时,会自动反序列化meta-data内的内容,这里就是我们反序…...

Rust安装
目录 一、安装1.1 在Windows上安装1.2 在Linux下安装 二、包管理工具三、Hello World3.1 安装IDE3.2 输出Hello World 一、安装 1.1 在Windows上安装 点击页面 安装 Rust - Rust 程序设计语言 (rust-lang.org),选择"下载RUSTUP-INIT.EXE(64位)&qu…...

513.找树左下角的值
给定一个二叉树,在树的最后一行找到最左边的值。 示例 1: 示例 2: 思路: 深度最大的叶子结点一定是最后一行。 优先左边搜索,记录深度最大的叶子节点,此时就是树的最后一行最左边的值 代码: class Solution:def fi…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
