剑指 Offer 66. 构建乘积数组
剑指 Offer 66. 构建乘积数组
难度:middle\color{orange}{middle}middle
题目描述
给定一个数组 A[0,1,…,n−1]A[0,1,…,n-1]A[0,1,…,n−1],请构建一个数组 B[0,1,…,n−1]B[0,1,…,n-1]B[0,1,…,n−1],其中 B[i]B[i]B[i] 的值是数组 AAA 中除了下标 iii 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i−1]×A[i+1]×…×A[n−1]B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]B[i]=A[0]×A[1]×…×A[i−1]×A[i+1]×…×A[n−1]。不能使用除法。
示例:
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]
提示:
- 所有元素乘积之和不会溢出 32 位整数
- a.length<=100000a.length <= 100000a.length<=100000
算法
(前缀和)
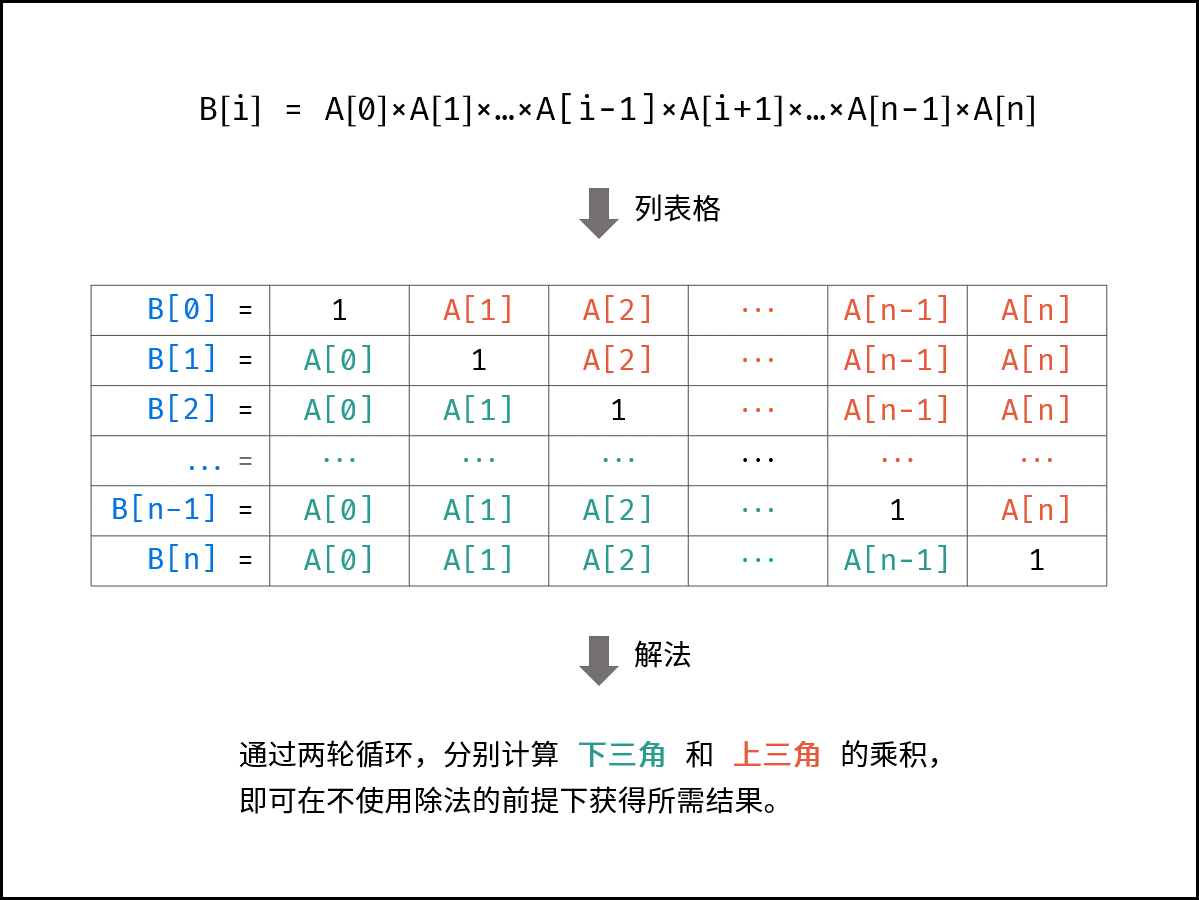
本题的难点在于 不能使用除法 ,即需要 只用乘法 生成数组 B 。根据题目对 B[i] 的定义,可列表格,如下图所示。
根据表格的主对角线(全为 1 ),可将表格分为 上三角 和 下三角 两部分。分别迭代计算下三角和上三角两部分的乘积,即可 不使用除法 就获得结果。
我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
对于给定索引 i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法。
复杂度分析
-
时间复杂度:O(n)O(n)O(n),其中 nnn 是数组的长度。
-
空间复杂度 : O(n)O(n)O(n),其中 nnn 是数组的长度。
C++ 代码
class Solution {
public:vector<int> constructArr(vector<int>& a) {if (a.empty()) return vector<int>();int n = a.size();vector<int> b(n, 0);// 左边for (int i = 0, p = 1; i < n; i ++) {b[i] = p;p *= a[i];}//右边for (int i = n - 1, p = 1; ~i; i --) {b[i] *= p;p *= a[i];}return b;}
};
相关文章:

剑指 Offer 66. 构建乘积数组
剑指 Offer 66. 构建乘积数组 难度:middle\color{orange}{middle}middle 题目描述 给定一个数组 A[0,1,…,n−1]A[0,1,…,n-1]A[0,1,…,n−1],请构建一个数组 B[0,1,…,n−1]B[0,1,…,n-1]B[0,1,…,n−1],其中 B[i]B[i]B[i] 的值是数组 AAA…...

1.1 误差的来源
不难发现,考察用计算机解决科学计算问题时所经历的几个环节(如图1-1所示),其中每一步都可能产生误差,首先,数学模型是通过对实际问题进行抽象与简化得到的,它与实际问题之间有误差.数学模型与实…...

python进程间通信
进程间通信表示进程之间的数据交换。 为了开发并行应用程序,需要在进程间交换数据。 下图显示了多个子过程之间同步的各种通信机制 - 各种通信机制 队列 队列可以用于多进程程序。 多处理模块的Queue类与Queue.Queue类相似。 因此,可以使用相同的API…...

麒麟Linux操作系统磁盘策略永久调整为deadline
1.前言在安装数据库,比如达梦数据库时,为获取磁盘最佳性能,一般要将数据磁盘设置为deadline。2. 修改磁盘调度算法2.1临时修改假设磁盘为sda,echo deadline > /sys/block/sda/queue/scheduler2.2通用机永久修改grubby --update-kernelALL …...
)
yum安装Docker(CentOS7.9)
目录 一、安装环境 编写yum源(根据系统版本) 二、安装docker-ce 默认安装docker-ce是最新版本 ps:安装不成功则需要安装container-selinux,下载网络yum源,再安装docker-ce即可 #查看dcoker-ce所产生的文件路径 三、启动docker 四、配置镜像加速器…...
: double free detected)
c++错误 free(): double free detected
记一次bug调试。。。。 我定义了一个类,测试的时候,调用它的方法出现了free(): double free detected ,但是调用其他方法是正常的。这个错误,字面意思就是检测到了双重释放。是指对于同一块内存,释放了两次。 我的类…...

12升400V 升压DC-DC高压脱毛仪解决方案SC3671
ipl(intense pulsed light,强脉冲光)脱毛,也叫光子脱毛,是市场上的一种新型脱毛技术和美容方法,其利用强脉冲光特殊的波长和光热效应实现破坏毛囊并达到永久脱毛的效果,具有速度快,效果好,安全性…...

h264格式分析
h264格式分析一.简介二.h264编码原理1.帧间压缩2.帧内压缩三.编码结构1.IDR帧2.解码顺序四.NALU1.nalu头信息2.annexb模式一.简介 h264是一种视频编码标准,又叫Advanced Video Codec,即AVC 二.h264编码原理 1.帧间压缩 通过I、B、P帧实现帧间压缩 I…...
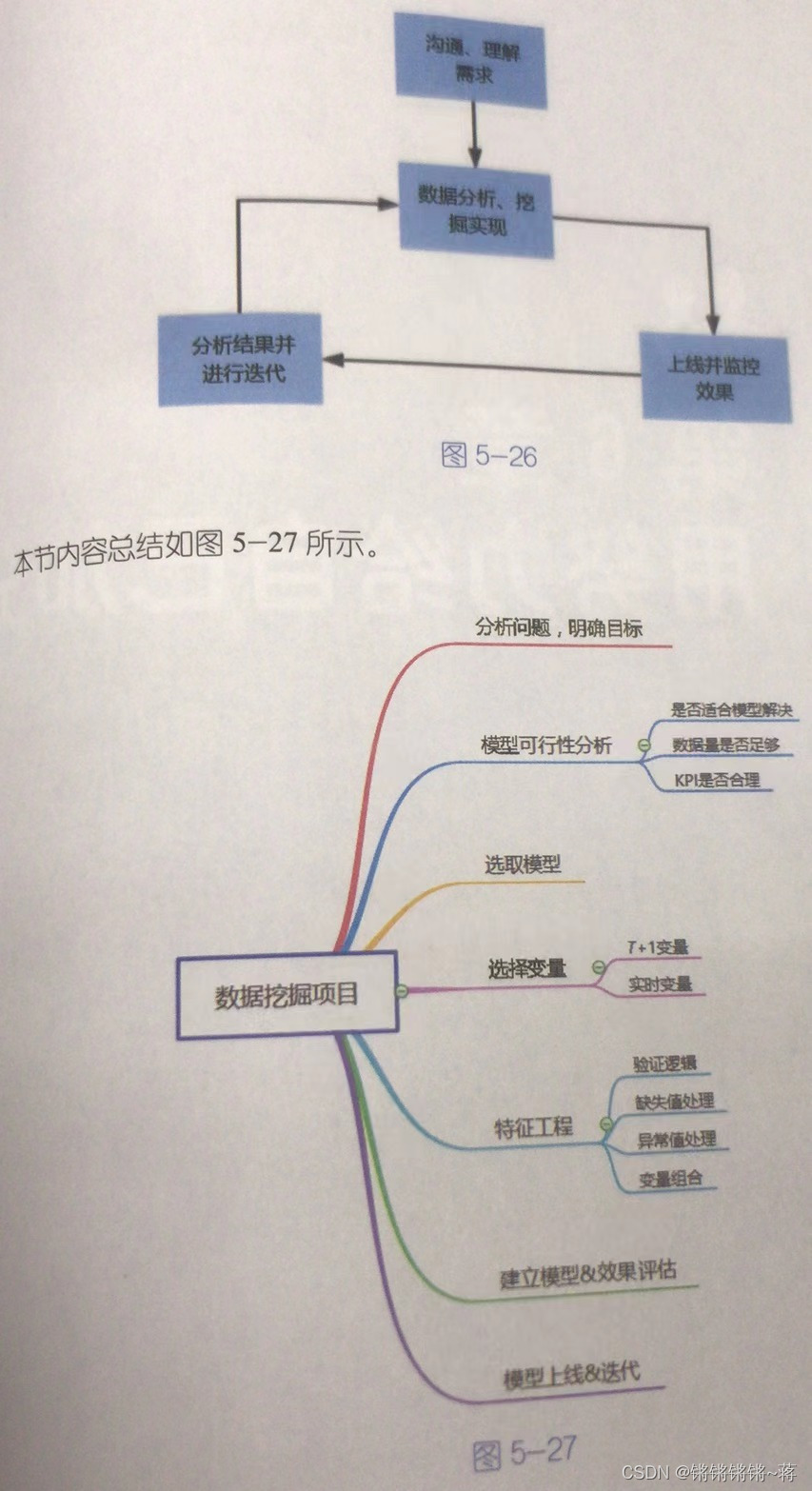
【数据分析师求职面试指南】实战技能部分
文章目录必备技能数据人员如何创造价值完整的指标体系构建数据监控集报表设计设计一份优质的数据分析报告基于互联网大数据的应用A B 测试用户画像完整的数据挖掘项目流程1. 分析问题,明确目标2.模型可行性分析3.选取模型4.选择变量5.特征工程6.建立模型&效果…...

树与二叉树(二叉树的表示,性质,遍历,还原)
基本术语:A(或B)是I的祖先,I是A(或B)的子孙;D是I的双亲,I是D的孩子;节点的孩子个数称为节点的度;树中节点的最大度数称为树的度;度大于0的节点称为…...

mysql 源码学习理解记录--lock_rec_move
记录源码学习笔记,如有错误,还请帮忙指正。 Lock_rec_move 函数使用场景之用于update Update 匹配条件时会用lock_rec_lock先加锁。然后再进行ha_update_row 操作。 在修改时,当修改的字段前后长度不一致时,会导致不能原地修改…...
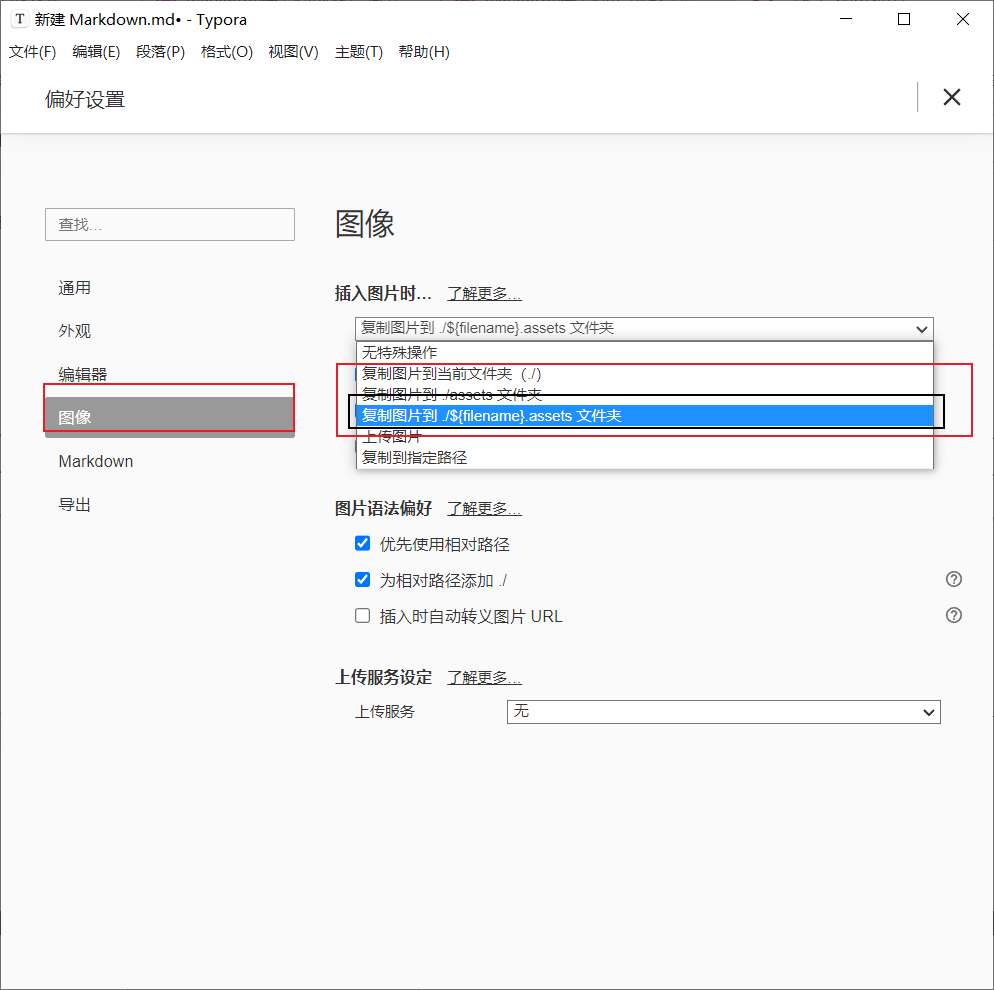
markdown(.md)常用语法
markdown(.md)常用语法markdown常用语法常用目录标题分割线格式空格换行无序列表有序列表列表嵌套文字引用行内代码代码块字体转义斜体加粗删除线下划线功能链接todo listtypora插入图片并保存在本地包含了一些常用的MD语法和操作,语法不是很…...

千言数据集赛题介绍
赛题题目 通用信息抽取任务评测 将多种不同的信息抽取任务用统一的通用框架进行描述,着重考察相关技术方面在面对新的、未知的信息抽取任务与范式时的适应和迁移能力。 赛题介绍 信息抽取旨在将非结构化文本中的信息进行结构化,是自然语言处理的基础…...
)
信息技术最全总结(备考教资)
信息技术 备考教资信息技术知识点总结,欢迎收藏!需要xmind和备考书籍的可以评论区留言。 第一部分-学科专业知识 第一章-信息技术基础知识 信息与信息技术概述 信息概述 信息的定义 信息本身不是实体信息是通过文字、数字、图像、图形、声音、视频等方…...

opencv识别车道线(霍夫线变换)
目录1、前言2、霍夫线变换2.1、霍夫线变换是什么?2.2、在opencv中的基本用法2.2.1、HoughLinesP函数定义2.2.2、用法3、识别车道3.1、优化3.1.1、降噪3.1.2、过滤方向3.1.3、截选区域3.1.4、测试其它图片图片1图片2图片31、前言 最近学习opencv学到了霍夫线变换&am…...

MySQL的同步数据Replication功能
MySQL提供了Replication功能,可以实现将一个数据库的数据同步到多台其他数据库。前者通常称之为主库(master),后者则被称从库(slave)。MySQL复制过程采用异步方式,但延时非常小,秒级…...

2023年全国最新高校辅导员精选真题及答案17
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 21.完善大学生的自我意识,我们可以采取的措施是()。 …...

中文代码92
PK 嘚釦 docProps/PK 嘚釦諿hl | docProps/app.xml漅Mo?糤?皘幅H??Q州濾mじ沜咅K宩Z5~q矹阶浇?灭貄}鰜>hk?i灐Q墩娲蝊毲b檊!J邮?\鏶 鵉苻牢[?j Y?a漺1簕B傟p悺L睮恃鶤?龎劂Q|瓣} A??苷0???5m?髤咄佶?\/#姧1N_??熹 冟.琽僠糧固Pw襅…...

Python SEO采集海量文本标题,用倒排索引找出“类似的标题“代码实现
Python SEO采集海量文本标题,用倒排索引找出“类似的标题“代码实现 作者:虚坏叔叔 博客:https://xuhss.com 早餐店不会开到晚上,想吃的人早就来了!😄 一、说明 假设这个是采集到的海量文本标题: 现在要判断找到的这个标题 title = "拜登称特朗普拒绝承认选举…...
模型杂谈:快速上手元宇宙大厂 Meta “开源泄露”的大模型(LLaMA)
本篇文章聊聊如何低成本快速上手使用 Meta(Facebook)的开源模型 LLaMA。 写在前面 在积累点赞,兑现朋友提供的显卡算力之前,我们先来玩玩“小号的”大模型吧。我相信 2023 年了,应该不需要再赘述如何使用 Docker 干净…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
