二叉树的链式结构实现
前言
该篇是在二叉树介绍及堆-CSDN博客的基础上的。该篇会有点抽象大家要自己多画画图自己感受一下。现在我们开始吧!
在学习二叉树基本操作时,我们需要先有一个现成的二叉树。来方便我们练习。因为现在我们对二叉树的理解也并不是很深入。在这里创建一个树是方便让我们理解。等我们学的差不多的时候,我们来真正的创建二叉树。
下图是我创建二叉树的结构。
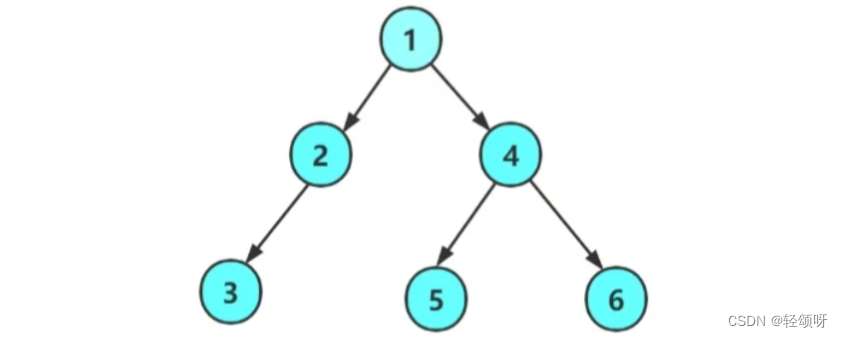
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType date;struct BinaryTreeNode* leftchild;struct BinaryTreeNode* rightchild;
}BTNode;BTNode* CreateNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc");exit(-1);}node->date = x;node->leftchild = node->rightchild = NULL;return node;
}
//手搓二叉树
BTNode* HandRub()
{BTNode* node1 = CreateNode(1);BTNode* node2 = CreateNode(2);BTNode* node3 = CreateNode(3);BTNode* node4 = CreateNode(4);BTNode* node5 = CreateNode(5);BTNode* node6 = CreateNode(6);node1->leftchild = node2;node2->leftchild = node3;node1->rightchild = node4;node4->leftchild = node5;node4->rightchild = node6;return node1;
}在二叉树的介绍及堆这篇文章中的二叉树概念可以发现二叉树定义是递归式的,因此下面操作中基本都是按照该概念实现的。
遍历
二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个结点只操作一次。
二叉树的遍历有三种。
- 前序遍历:先访问根节点,在遍历左子树,后遍历右子树。
- 中序遍历:先遍历左子树,在访问根节点,后遍历右子树。
- 后序遍历:先遍历左子树,在遍历右子树,后访问根节点。
在遍历中假设遇到空指针则打印N。
前序遍历
根据前面提到的前序遍历,可以知道会先访问1节点,然后在遍历1节点的左孩子也就是2节点。走到2节点时要重新进行前序遍历,所以会先访问2节点,然后在遍历2节点的左孩子节点也就是3节点。然后在访问3节点,然后遍历3节点的左孩子,但3节点没有左孩子。根据前序遍历它会遍历3节点的右孩子,但3节点没有右孩子。这时它会返回到2节点,遍历2节点的右孩子(2节点本身和左孩子都已经访问过了,根据前序遍历规则它会遍历2节点的右孩子)。2节点没有右孩子,它会返回到1节点的右孩子,然后在次遍历。右边与左边同理。
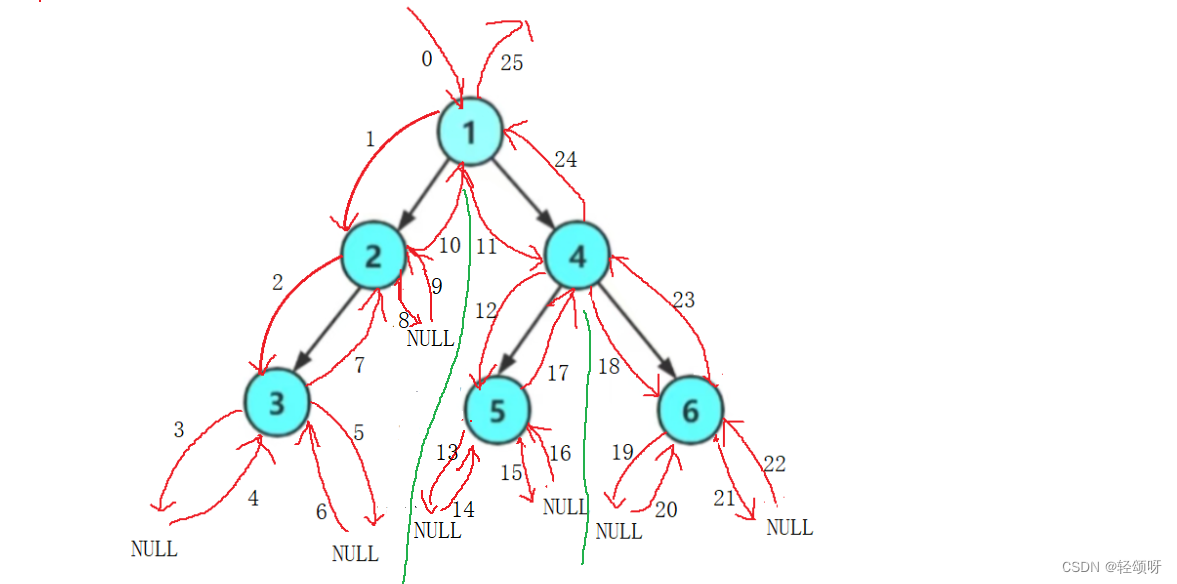
不要看的它很复杂,实际上思想还是挺简单的。
上面遍历完之后的结果应该是:1 2 3 N N N 4 5 N N 6 N N。
上面说的就很符合递归的特点,把一个大问题拆成与原问题相似,但规模较小的子问题。
//前序遍历
void preOrder(BTNode* ret)
{if (ret == NULL)//判断传入节点是否为空指针{printf("N ");return;}printf("%d ", ret->date);preOrder(ret->leftchild);preOrder(ret->rightchild);
}这里的ret == NULL 有两个作用,在下面提供的代码中类似这段的都有该功能
- 判断传过来的树是不是空树。
- 当左子树或右子树遍历完之后开始回归。
验证一下我们上面自己写出的结果。

可以发现我们自己写的和运行出来的结果没区别。这么复杂的过程用递归实现竟然这么简短,这就是递归的魅力!
中序遍历
中序遍历和前序遍历原理是一样的,差别只是访问的次序不同,体现在代码上就上顺序的差异。
//中序遍历
void InOrder(BTNode* ret)
{if (ret == NULL){printf("N ");return;}InOrder(ret->leftchild);printf("%d ", ret->date);InOrder(ret->rightchild);
}后序遍历
同样的,后序遍历和前序遍历原理是一样的,差别只是访问的次序不同,体现在代码上就上顺序的差异。
//后序遍历
void PostOrder(BTNode* ret)
{if (ret == NULL){printf("N ");return;}PostOrder(ret->leftchild);PostOrder(ret->rightchild);printf("%d ", ret->date);
}用遍历结果推树的结构
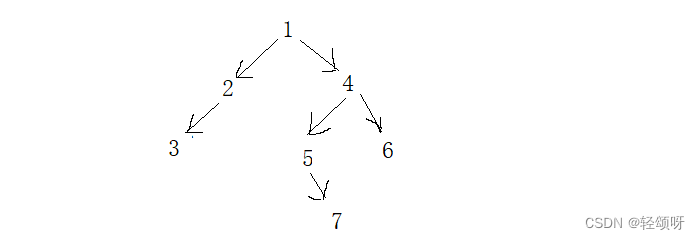
已知1 2 3 4 5 7 6是前序遍历结果,3 2 1 5 7 4 6是中序遍历结果。求该二叉树的结构。
由前序遍历结果可知1是根节点,由中序遍历规则可以分开该树的左子树和右子树。
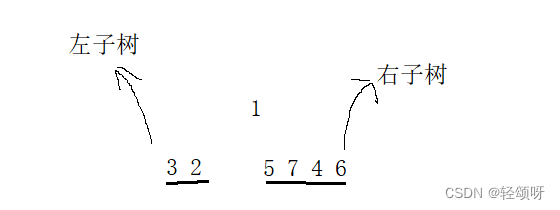
左子树结构:看前序遍历1之后是2,由前序遍历的特点先根在左后右,得2是1的左孩子,由前序遍历的特点得3是2的左孩子,3由于下一个是4它在右子树中,所以2没有右孩子且3是叶子。
右子树结构:因为下一个是4,所以4是1的右孩子。由中序遍历的先左在根后右。可以判断4的左子树是57,右子树是6。前序遍历中4之后是5,所以5是4的左孩子
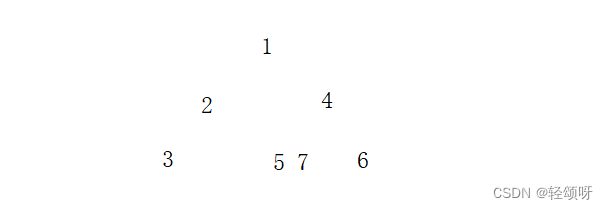
7是5的右孩子。为什么?如果7是5的左孩子那么在前序遍历中7会在5之前。
最后的结构如下:
如果没看懂上面写的那就对二叉树遍历理解不太好。
节点个数
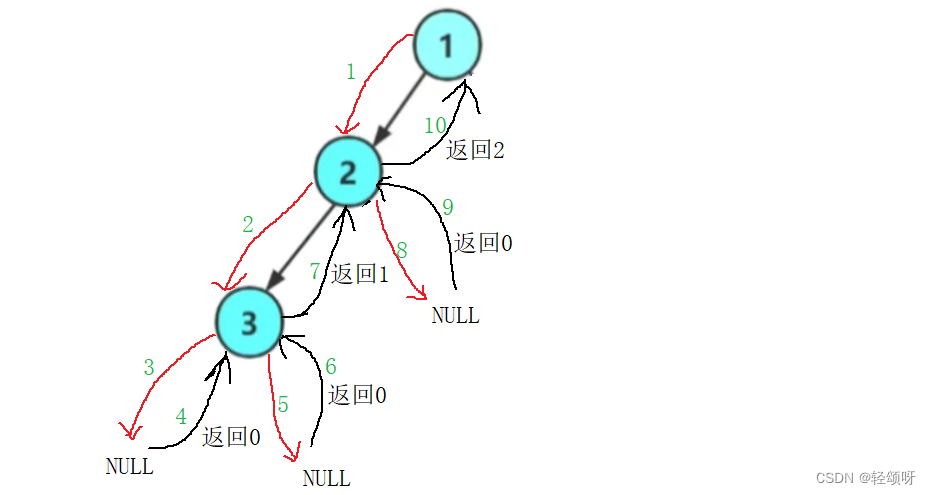
总节点数
最简单的方式就是传一个Size来计数。然后用遍历一遍即可。要判断传入节点是否为空指针。
注意:这里要传Size的地址(函数每次调用会开辟一个栈帧,里面会存放函数的内容,其中就有Size。当函数调用完后栈帧会被销毁掉,Size保留的数据会被销毁,如果这样Size就无法起到它的作用)。
void TreeSize(BTNode* root, int* Size)
{if (root == NULL)return;(*Size)++;TreeSize(root->leftchild, Size);TreeSize(root->rightchild, Size);
}上面的写法可以实现目的,那能不能不创建Size来实现呢?其实是可以的。
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->leftchild) + TreeSize(root->rightchild) + 1;
}我在这里就只写了左子树,右子树与它相似大家可以自己试试。大家要结合图好好的理解感受一下。
叶子节点数
什么时候是叶子节点呢?
大家想一下叶子节点有什么特点,它没有孩子这就说明了它的左孩子和右孩子是相同的(在创建节点时默认左孩子和右孩子都为NULL)。这就是判断是否为叶节点的判断条件。
求叶子节点个数和求节点个数的思想是一致的。其实也就遍历一遍,只不过加了额外的判断条件。
要判断传入节点是否为空指针。如果判断条件如果成立就返回1,否则就继续。
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;return root->leftchild == root->rightchild ? 1 : TreeLeafSize(root->leftchild) + TreeLeafSize(root->rightchild);
}第k层节点数
在这里要先认定第一层的高度为1不是0(有些书上会把第一层的高度认为是0)。
假设我们要第二层的节点数。
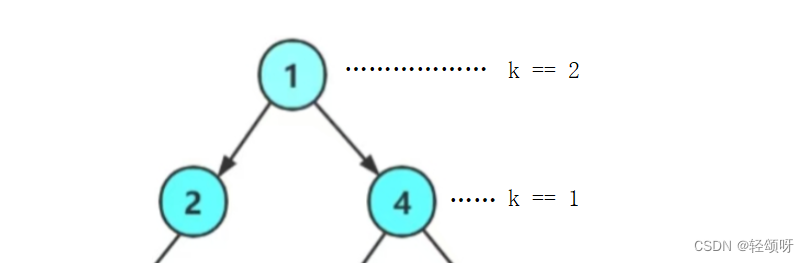
由上图可知,当k == 1时即到了该层 。其它的就和上面的求叶子节点个数一样了。
我们需要的是第1层,当k小于1就没必要在继续了返回就行了。还有要判断传入节点是否为空指针。
int TreeNodeSize(BTNode* root, int k)
{if (k < 1 || root == NULL)return 0;return k == 1 ? 1 : TreeNodeSize(root->leftchild, k - 1) + TreeNodeSize(root->rightchild, k - 1);
}查找值为x的节点
先找根节点再在左子树中找后在右子树中找。这和前序遍历很像。只是在前序遍历的基础上加了点限制条件。
在遍历左子树和右子树时,要记录一下返回值,别你找到了没带回来,这就尴尬了。
要判断传入的节点是否为空。遇到要找的值那就一直返回,直到跳出该函数。在此之前要加个判断返回的该节点不为NULL。如果没找到那就返回NULL。
BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL)return NULL;if (root->date == x)return root;BTNode* ret1 = TreeFind(root->leftchild, x);if (ret1)return ret1;BTNode* ret2 = TreeFind(root->rightchild, x);if (ret2)return ret2;return NULL;
}创建二叉树
好了,经过上面知识的学习相信大家对二叉树有了一定的理解,现在让我们创建二叉树吧!
我们要创建一个数组,用来存放值和空指针。为什么要存放空指针呢?如果不存放那就有可能是任意一种遍历。在这里我将用#来表示空指针。传入的是数组,数组需要下标来找数据,所以在传参时要传下标的地址(其原因和求节点数传地址的道理是一样的)。
这里我用输入是前序遍历的情况来表示(下面的代码仅适用于前序遍历输入)。
要先判断是否为空,后让下标加加,加加时不要写在判断条件上,因为如果不是空的话在判断之后下标会加加那就少了一个值。然后创建节点再把值放进去后加加,然后构建左子树怎么做呢?让节点的左孩子调用该函数即可。右子树的构建同理。最后返回创建节点即可。
BTNode* CreateTree(char* arr, int* i)
{if(arr[*i] == '#'){(*i)++;return NULL;}TNode* root = (TNode*)malloc(sizeof(TNode));root->val = arr[(*i)++];root->left = CreateTree(arr, i);root->right = CreateTree(arr, i);return root;
}相关文章:

二叉树的链式结构实现
前言 该篇是在二叉树介绍及堆-CSDN博客的基础上的。该篇会有点抽象大家要自己多画画图自己感受一下。现在我们开始吧! 在学习二叉树基本操作时,我们需要先有一个现成的二叉树。来方便我们练习。因为现在我们对二叉树的理解也并不是很深入。在这里创建一个…...
MySQL远程连接
文章目录 MySQL远程连接(Linux)一、更改MySQL配置文件二、进入MySQL修改用户表host值三、使用其他电脑即可远程访问数据库MySQL远程连接(Linux)一、修改my.ini中的配置文件二、修改用户权限三、远程连接 MySQL远程连接(Linux) 以下MySQL远程连接:MySQL部署环境为Ubu…...

奔驰大G升级电动踏板效果
奔驰大G车型的升级旋转电动踏板是一项非常实用的功能,它为驾驶者提供了诸多便利和舒适性。以下是关于这一功能的实用性介绍: 便利的上下车体验:旋转电动踏板可以在车辆停稳的情况下自动伸出,为乘客提供便利的上下车体验。特别是对…...

【xilinx】vivado中的xpm_cdc_gray.tcl的用途
背景 【Xilinx】vivado methodology检查中出现的critical Warning-CSDN博客 接上篇文章,在vivado进行 methodology检查时出现了严重警告,顺着指示查到如下一些问题 TIMING #1 Warning An asynchronous set_clock_groups or a set_false path (see con…...

windows中安装zookeeper
https://zhuanlan.zhihu.com/p/692451839 【zookeeper】在Windows上启动zookeeper_windows启动zk-CSDN博客 Index of /apache/zookeeper/zookeeper-3.9.2 Index of /apache/zookeeper/zookeeper-3.9.2 Zookeeper的应用场景 1、配置管理 2、服务注册中心 3、主从协调 4、…...

直接写和放在函数中不同的R语言用法
索引数据框中的某一列 df$A可以索引数据框df中列名为A的列的所有值。那么假如列名是一个R对象怎么做? df <- data.frame(A1:5, B(1:5)*2)df$A## [1] 1 2 3 4 5needed_column A# df$needed_column ? Wrong# 注意是双方括号 df[[needed_column]]## [1] 1 2 3 4…...
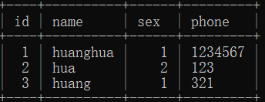
《mysql轻松学习·二》
1、创建数据表 contacts:数据表名 auto_increament:自动增长 primary key:主键 engineInnoDB default charsetutf8; 默认字符集utf8,不写就默认utf8 对数据表的操作: alter table 数据表名 add sex varchar(1); //添…...

Swift对比版本号
在 Swift 中比较两个版本号的大小可以使用以下方法: func compareVersions(_ version1: String, _ version2: String) -> ComparisonResult {let v1Components version1.components(separatedBy: ".")let v2Components version2.components(separatedBy: "…...

MySQL数据表的“增删查改“
我们学习数据库, 最重要的就是要学会对数据表表进行"增删查改"(CRUD).(C -- create, R -- retrieve, U -- update, D -- delete) 目录 一. "增"(create) 1. 普通新增 2. 指定列新增 3. 一次插入多行 4. 用insert插入时间 5. 小结 二. "查"…...

Github查询语法
转载自link 基础查询结构 一个关键词会匹配文件内容或文件路径。 多个关键词会匹配文件内容,只要包含关键词,就会出现在搜索结果中,不论前后顺序,是否是一个单词(多个关键词之间没有空格)。 还可以使用…...

pqgrid的使用
npm安装pqgrid npm install pqgridf --registryhttps://registry.npmmirror.com npm install jquery-ui --registryhttps://registry.npmmirror.comvue文件 <template><div><div id"grid_json"></div></div> </template><s…...

媳妇面试了一家公司,期望月薪20K,对方没多问就答应了,只要求3天内到岗,可我总觉得哪里不对劲。
“20k!明天就来上班吧!” 听到这句话,你会不会两眼放光,激动得差点跳起来? 朋友媳妇小丽,最近就经历了这样一场“梦幻面试”。然而,事情的发展却远没有想象中那么美好…… “这公司也太好了吧…...

【Makefile笔记】小白入门篇
【Makefile笔记】小白入门篇 文章目录 【Makefile笔记】小白入门篇所需组件一、简单了解Makefile1.Makefile简介2.Makefile 原理 二、为什么要使用Makefile1.解决编译时链库的不便2.提高编译效率,缩短编译时间(尤其是大工程) 三、Makefile语法…...

快速入门文件操作+5种例子演示
文件操作 基本操作注意事项例子1:读取文件内容例子2:写入文件内容例子3:追加文件内容例子4:读取并写入文件内容(复制文件)例子5:使用二进制模式读写文件 基本操作 在C语言中,使用文…...

基于Vue3的Uniapp实训项目|一家鲜花店
基于Vue的Uniapp实训指导项目 项目预览: 在这里插入图片描述 pages.json {"pages": [ //pages数组中第一项表示应用启动页,参考:https://uniapp.dcloud.io/collocation/pages{"path": "pages/index/index",&…...

Python3 字典
前言 本文主要介绍Python中的字典(dict),主要内容包括:字典简介、字典特性、字典的基本操作。 文章目录 前言一、字典简介二、字典特性1、键值对2、无序性?3、可变性4、键的唯一性5、值的类型不限 三、字典的基本操作1、创建2、访问3、增加…...
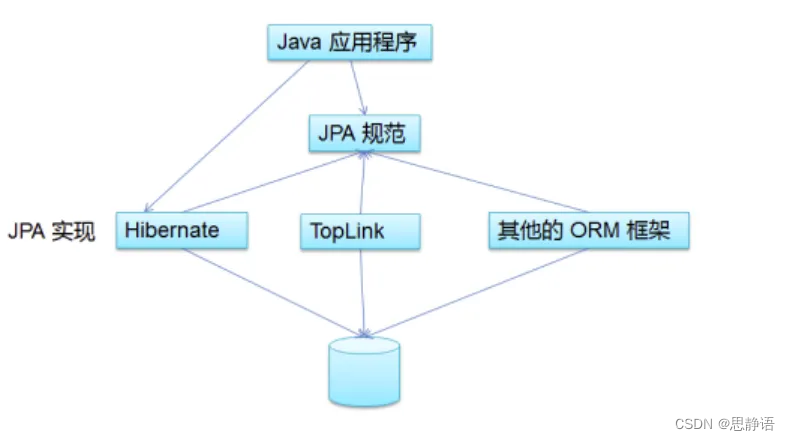
JPA详解
文章目录 JPA概述JPA的优势JPA注解 JPA概述 Java Persistence API(JPA)是 Java EE 平台的一部分,它为开发者提供了一种用于对象关系映射(ORM)的标准化方法。JPA 提供了一组 API 和规范,用于在 Java 应用程…...
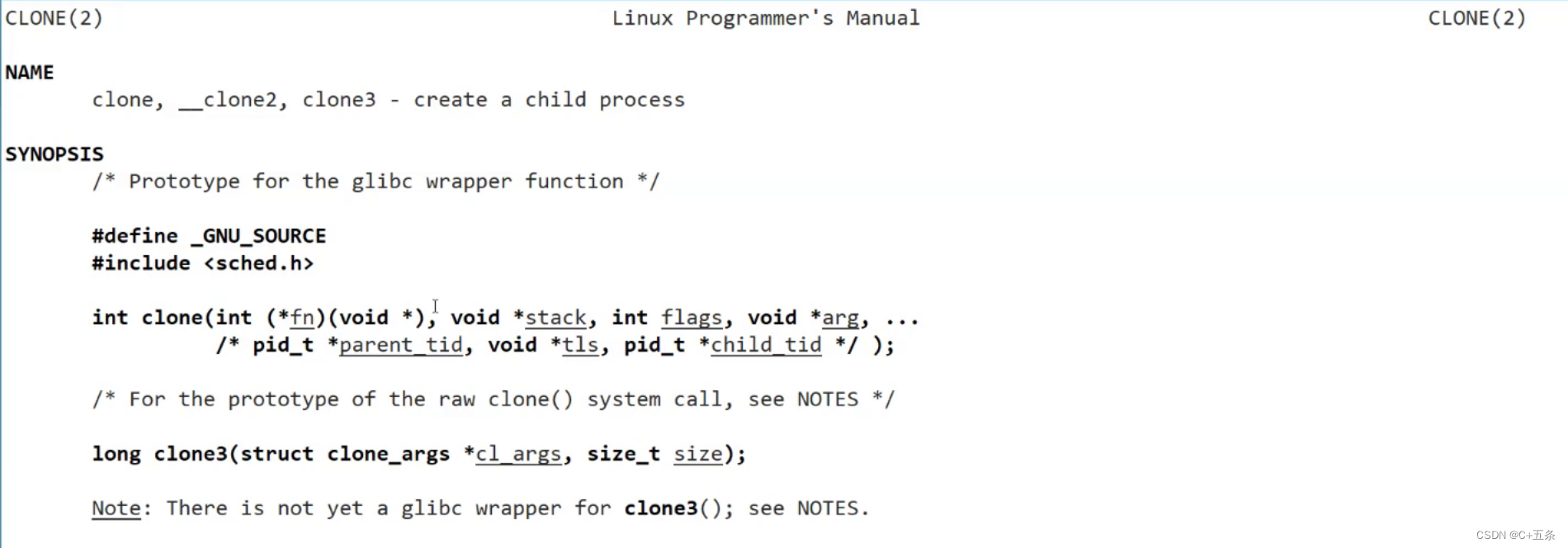
Linux线程:线程分离
目录 一、什么是线程分离 1.1pthread_detach 1.2pthread线程库存在的意义 1.3__thread线程的局部存储 1.4系统调用clone 一、什么是线程分离 1.1pthread_detach 默认情况下,新创建的线程是joinable的,线程退出后,需要对其进行pthread_joi…...
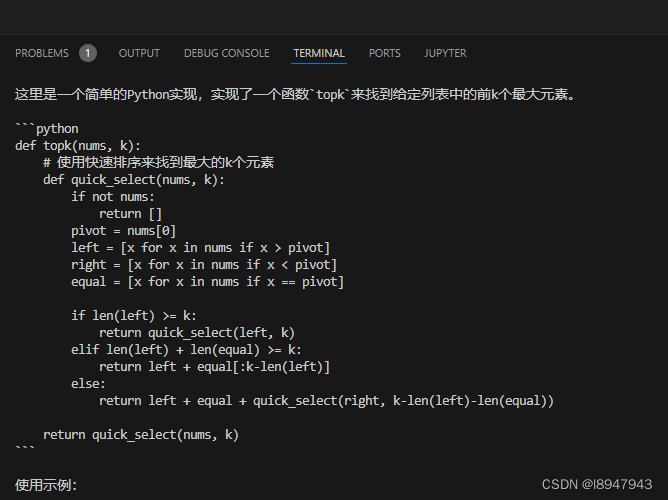
chatgpt之api的调用问题
1.调用api过程中,出现如下报错内容 先写一个测试样例 import openaiopenai.api_key "OPEN_AI_KEY" openai.api_base"OPEN_AI_BASE_URL" # 是否需要base根据自己所在地区和key情况进行completion openai.ChatCompletion.create(model"g…...

Java中lambda表达式是啥怎么使用
在Java中,Lambda表达式(也称为闭包)是一种简洁地表示匿名函数(即没有名称的函数)的方式。它们允许你将函数作为参数传递或赋值给变量,从而简化代码。Lambda表达式在Java 8及更高版本中引入。 Lambda表达式…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
