多项分布模拟及 Seaborn 可视化教程
多项分布
简介
多项分布是二项分布的推广,它描述了在 n 次独立试验中,k 种不同事件分别出现次数的离散概率分布。与二项分布只能有两种结果(例如成功/失败)不同,多项分布可以有 k 种(k ≥ 2)及以上的不同结果。
参数
多项分布用三个参数来定义:
n:试验次数,表示重复相同实验的次数。
pvals:一个长度为 k 的列表,其中每个元素表示对应结果出现的概率。pvals 的元素之和必须为 1。
size:输出数组的形状。
公式
多项分布的概率质量函数 (PMF) 给出了在 n 次试验中,k 种结果分别出现 k1、k2、…、kk 次的概率,计算公式为:
P(k1, k2, ..., kk) = n! / (k1! * k2! * ... * kk!) * (p1 ^ k1) * (p2 ^ k2) * ... * (pk ^ kk)
其中:
P(k1, k2, ..., kk):表示 k 种结果分别出现 k1、k2、…、kk 次的概率。
n!:n 的阶乘,即 n × (n - 1) × (n - 2) × … × 2 × 1。
k1!、k2!、…、kk!:k1、k2、…、kk 的阶乘,分别表示对应结果出现的次数的阶乘。
p1、p2、…、pk:对应结果出现的概率,分别为 pvals 列表中的元素。
生成多项分布数据
NumPy 提供了 random.multinomial() 函数来生成服从多项分布的随机数。该函数接受以下参数:
n:试验次数。
pvals:结果的概率列表。
size:输出数组的形状。
示例:生成掷骰子 10 次的结果,其中每个结果出现的概率相等:
import numpy as npdata = np.random.multinomial(n=10, pvals=[1/6] 6, size=1000)
print(data)
可视化多项分布
由于多项分布可以表示多种结果的出现次数,因此其可视化方式通常取决于结果的个数和想要展示的信息。
条形图:如果结果个数较少,可以使用条形图来直观地显示每个结果出现的次数。
堆积条形图:如果结果个数较多,可以使用堆积条形图来显示不同试验次数下每个结果出现的次数分布。
折线图:如果需要比较不同试验次数下每个结果出现的概率分布,可以使用折线图来绘制每个结果出现的概率随试验次数的变化情况。
练习
- 模拟 100 次掷骰子的结果,并绘制每个结果出现的次数分布图。
- 比较不同试验次数下掷骰子结果的分布变化。
- 模拟一个具有 3 种结果的抽奖活动,每个结果出现的概率分别为 1/3、1/2 和 1/6,并计算每种结果出现 1 次的概率。
解决方案
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt# 1. 模拟掷骰子结果并绘制分布图
data = np.random.multinomial(n=10, pvals=[1/6] 6, size=1000)
result_counts = data.sum(axis=0) # 计算每个结果出现的总次数
sns.barplot(x=np.arange(len(result_counts)), y=result_counts)
plt.xlabel("Result")
plt.ylabel("Count")
plt.title("Distribution of Dice Rolls (1000 trials)")
plt.show()# 2. 比较不同试验次数下分布变化
n_values = [10, 50, 100, 500]
for n in n_values:data = np.random.multinomial(n=n, pvals=[1/6] 6, size=1000)result_counts = data.sum(axis=0)sns.barplot(x=np.arange(len))
最后
为了方便其他设备和平台的小伙伴观看往期文章:
微信公众号搜索:Let us Coding,关注后即可获取最新文章推送
看完如果觉得有帮助,欢迎点赞、收藏、关注
相关文章:

多项分布模拟及 Seaborn 可视化教程
多项分布 简介 多项分布是二项分布的推广,它描述了在 n 次独立试验中,k 种不同事件分别出现次数的离散概率分布。与二项分布只能有两种结果(例如成功/失败)不同,多项分布可以有 k 种(k ≥ 2)及…...

学计算机,我错了吗?
今天,我的一位朋友告诉我,终于找到一家小公司入职,年前 1 月辞职,本想休息一段时间,没成想,休息到 6 月份,现在程序员真的越来越难找工作了。 肯定有人在想,现在这种行情࿰…...

学习小心意——简单的循坏语句
for循坏 基本语法格式 for 变量 in 序列:代码块 示例代码如下 for i in range(10):print(i)#输出结果:0 1 2 3 4 5 6 7 8 9 简单案例代码如下 利用for语句遍历序列 # 遍历字符串打印每个字母 for letter in "python":print(letter)# 遍历列表并打印每个元素 a …...

C++ 类方法解析:内外定义、参数、访问控制与静态方法详解
C 类方法 类方法,也称为成员函数,是属于类的函数。它们用于操作或查询类数据,并封装在类定义中。类方法可以分为两种类型: 类内定义方法: 直接在类定义内部声明和定义方法。类外定义方法: 在类定义内部声明方法,并在…...
pytorch+YOLOv8-1
1.工具开发 2.idea配置pytorch环境 默认安装新版本torch pip install torch 3.pytorch验证 4. print(torch.cuda.is_available()) 输出结果为 False 说明我只能用cpu...

JavaScript 基础 - 对象
对象 对象是一种无序的数据集合,可以详细的描述描述某个事物。 注意数组是有序的数据集合。它由属性和方法两部分构成。 语法 声明一个对象类型的变量与之前声明一个数值或字符串类型的变量没有本质上的区别。 <script>let 对象名 {属性名:属性值…...

代码随想录第23天|回溯part3 组合与分割
39.组合总和 class Solution { public:vector<vector<int>> res;vector<int> path;void backTracking(vector<int>& candidates,int target,int sum,int n,int step){if(n > 150) return;if(sum > target) return;if(sum target){res.push_…...

nginx和proxy_protocol协议
目录 1. 引言2. HTTP server的配置3. Stream server的配置3.1 作为proxy_protocol的前端服务器3.2 作为proxy_protocol的后端服务器1. 引言 proxy_protocol 是haproxy开发的一种用于在代理服务器和后端服务器之间传递客户端连接信息的协议。使用 proxy_protocol 的主要优势是能…...

【pytorch】数据转换/增强后保存
数据转换 from PIL import Image from pathlib import Path import matplotlib.pyplot as plt import numpy as npimport torch import torchvision.transforms as Tplt.rcParams["savefig.bbox"] = tight # orig_im...
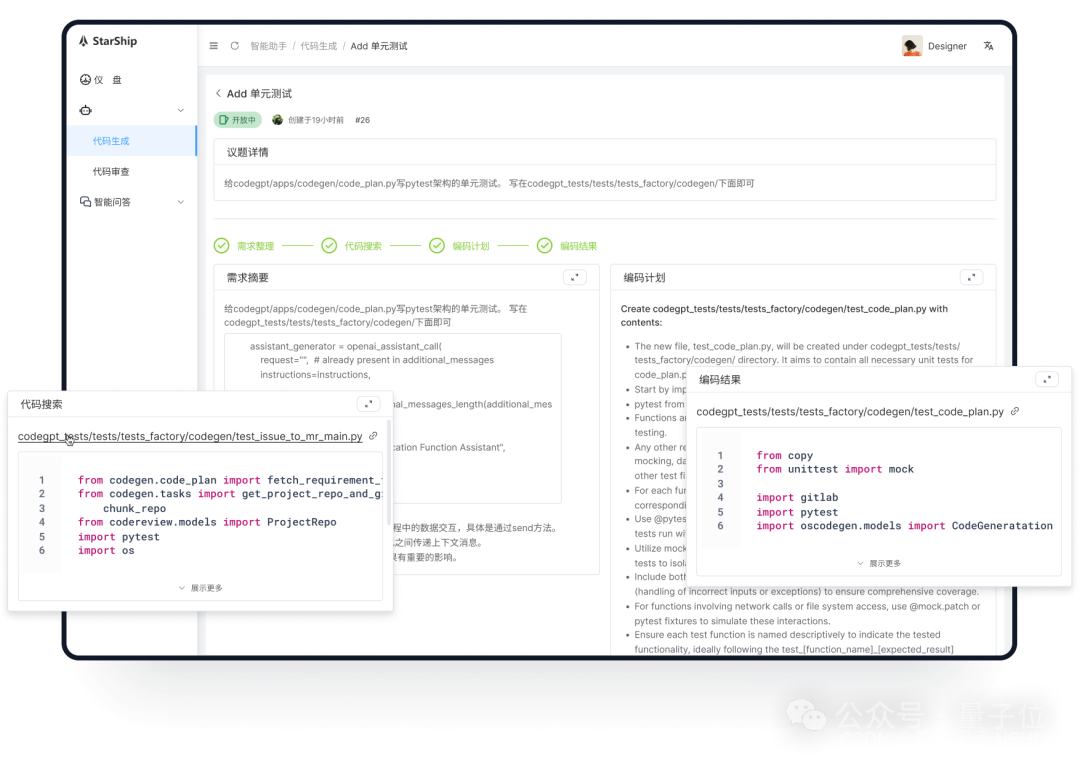
超越Devin!姚班带队,他们创大模型编程新世界纪录
超越Devin!SWEBench排行榜上迎来了新玩家—— StarShip CodeGen Agent,姚班带队初创公司OpenCSG出品,以23.67%的成绩获得全球第二名的成绩。 同时创造了非GPT-4o基模的最高纪录(SOTA)。 我们都知道,SWEBe…...

江苏大信环境科技有限公司:环保领域的开拓者与引领者
2009 年,江苏大信环境科技有限公司在宜兴环保科技工业园成立。自创立之始,该公司便笃定坚守“诚信为本、以质量求生存、以创新谋发展”这一经营理念,全力以赴为客户构建专业的工业有机废气治理整体解决方案,进而成为国家高新技术企…...

关于 Bean 容器的注入方式,99 % 的人都答不全!
引言:在使用 Spring 框架开发应用程序时,依赖注入是一个至关重要的概念。而对于 Bean 容器的注入方式,虽然我们可能都有一定的了解,但实际上很多人在被问及这个问题时可能并不能完整地回答。本文将深入探讨 Spring 中 Bean 容器的…...

Spring的@Async注解及其用途
Spring 的 Async 注解是 Spring Framework 4.2 版本引入的功能,它用于支持异步方法执行。当一个方法标注了 Async,Spring 会在一个单独的线程中调用该方法,从而不会阻塞主线程的执行。 Async 注解的用途: 提高性能:通…...
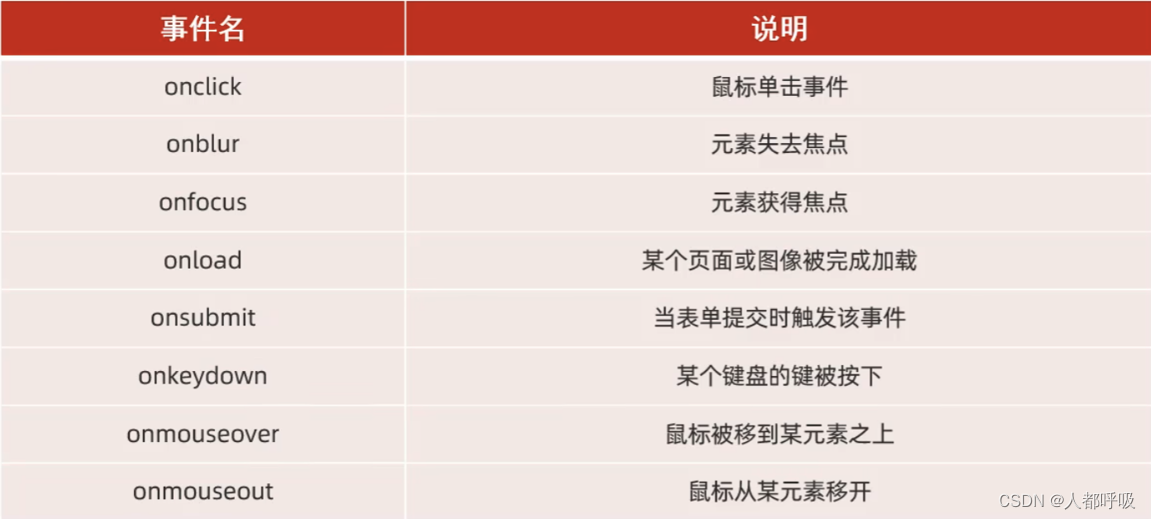
JS(DOM、事件)
DOM 概念:Document Object Model,文档对象模型。将标记语言的各个组成部分封装为对应的对象: Document:整个文档对象Element:元素对象Attribute:属性对象Text:文本对象Comment:注释对象 JavaScript通过DOM,就能够对HTML进行操作: 改变 HTML 元素的内…...

学习小心意——python的构造方法和析构方法
构造方法和析构方法分别用于初始化对象的属性和释放类占有的资源 构造方法_init_() 语法格式如下: class 类名:def __init__(self, 参数1, 参数2, ...):# 初始化代码self.属性1 参数1self.属性2 参数2# ... 示例代码如下 class Student:def __init__(self):s…...

GB/T 23995-2009 室内装饰装修用溶剂型醇酸木器涂料检测
溶剂型醇酸木器涂料是指以醇酸树脂为主要成膜物,通过氧化干燥成膜的溶剂型木器涂料适用于室内木制品表面的保护及装饰。 GB/T 23995-2009室内装饰装修用溶剂型醇酸木器涂料检测项目: 测试指标 测试方法 在容器中状态 GB/T 23995 细度 GB/T 6753.1 …...
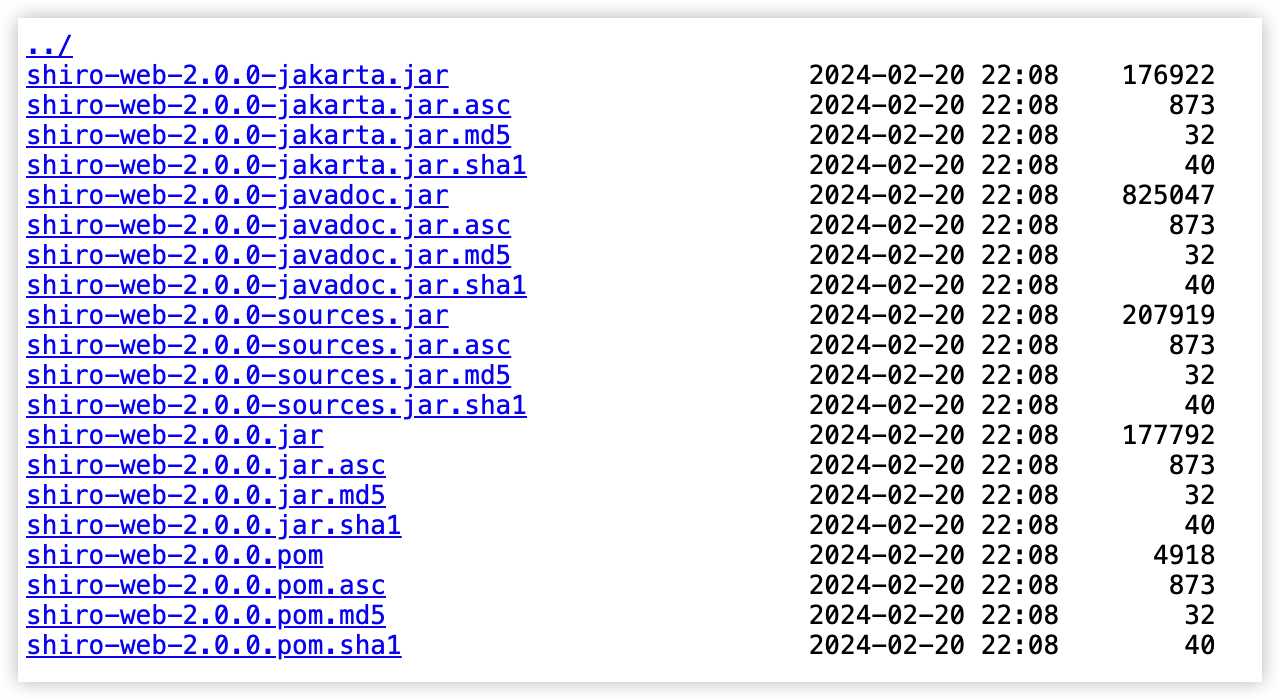
Maven 中的 classifier 属性用过没?
最近训练营有小伙伴问到松哥一个关于 Maven 依赖的问题,涉及到 classifier 属性,随机问了几个小伙伴,都说工作中没用到过,因此简单整篇文章和小伙伴们分享下。 Maven 大家日常开发应该都有使用,Maven 中有一个比较好玩…...
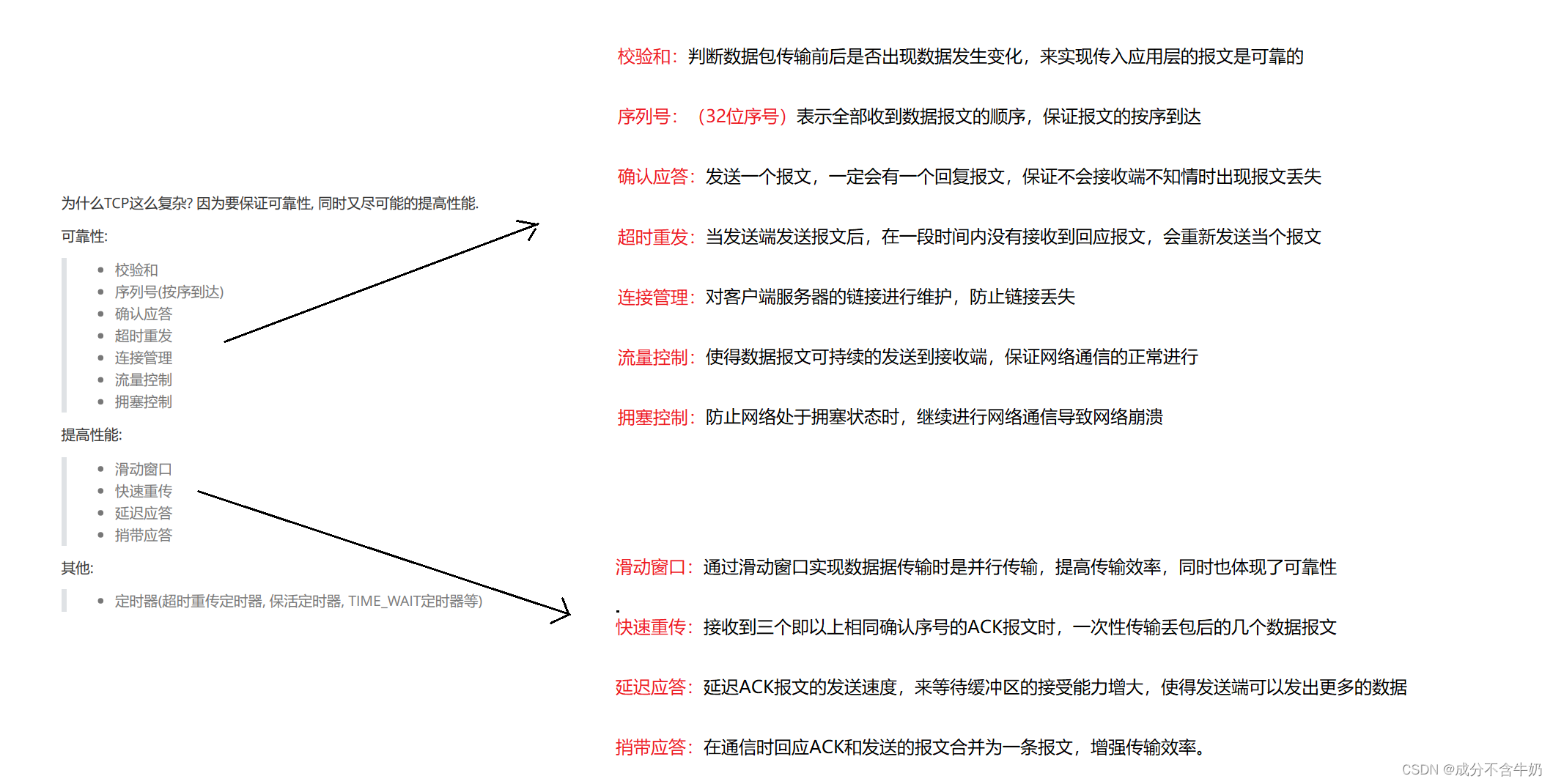
Linux网络编程:传输层协议|UDP|TCP
知识引入: 端口号: 当应用层获得一个传输过来的报文时,这时数据包需要知道,自己应该送往哪一个应用层的服务,这时就引入了“端口号”,通过区分同一台主机不同应用程序的端口号,来保证数据传输…...

MongoDB CRUD操作:内嵌文档查询
MongoDB内嵌文档的查询 文章目录 MongoDB内嵌文档的查询使用点号.查询内嵌文档嵌套字段的相等匹配使用查询操作符进行匹配指定AND条件 嵌套文档的匹配使用 MongoDB Atlas 查询内嵌文档导航至集合指定查询过滤文档点击应用 可以使用下面几种方法查询MongoDB中的嵌入文档…...

JavaScript、Kotlin、Flutter可以开发鸿蒙APP吗?
自从去年华为宣布推出「鸿蒙Next」版本开始,标志着其操作系统的全面革新。鸿蒙Next将摒弃所有基于AOSP的代码,与Android系统彻底分离,实现完全自主的研发路径。通过精简约40%的冗余代码,鸿蒙Next致力于构建一个更高效、更流畅的系…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
