GB/T 23995-2009 室内装饰装修用溶剂型醇酸木器涂料检测
溶剂型醇酸木器涂料是指以醇酸树脂为主要成膜物，通过氧化干燥成膜的溶剂型木器涂料适用于室内木制品表面的保护及装饰。
GB/T 23995-2009室内装饰装修用溶剂型醇酸木器涂料检测项目：
| 测试指标 | 测试方法 |
| 在容器中状态 | GB/T 23995 |
| 细度 | GB/T 6753.1 |
| 干燥时间 | GB/T 1728 |
| 贮存稳定性 | GB/T 23995 |
| 涂膜外观 | GB/T 23995 |
| 光泽度 | GB/T 9754 |
| 附着力 | GB/T 9286 |
| 耐干热性 | GB/T 4893.3 |
| 耐水性 | GB/T 23995 |
| 耐碱性 | GB/T 23995 |
| 耐污染性 | GB/T 23995 |
相关标准：
GB 14907-2018 钢结构防火涂料
GB 12441-2018 饰面型防火涂料
GB 28374-2012 电缆防火涂料
JC/T 1040-2020建筑外表面用热反射隔热涂料
广州通用检测技术服务有限公司建材产品检测服务：
陶瓷砖，石材，水泥纤维板，硅酸钙板，WPC地板，人造板，铝塑板，架高地板，轻质隔墙板，石膏板，轻钢龙骨，天花吊顶，建筑玻璃，门窗五金，SPC地板，木地板，PVC地板，保温隔热材料，功能材料……
广州通用检测技术服务有限公司认证服务：
法国A+认证，绿色建材认证，CE认证……
相关文章：
GB/T 23995-2009 室内装饰装修用溶剂型醇酸木器涂料检测
溶剂型醇酸木器涂料是指以醇酸树脂为主要成膜物，通过氧化干燥成膜的溶剂型木器涂料适用于室内木制品表面的保护及装饰。 GB/T 23995-2009室内装饰装修用溶剂型醇酸木器涂料检测项目： 测试指标 测试方法 在容器中状态 GB/T 23995 细度 GB/T 6753.1 …...
Maven 中的 classifier 属性用过没？
最近训练营有小伙伴问到松哥一个关于 Maven 依赖的问题，涉及到 classifier 属性，随机问了几个小伙伴，都说工作中没用到过，因此简单整篇文章和小伙伴们分享下。 Maven 大家日常开发应该都有使用，Maven 中有一个比较好玩…...
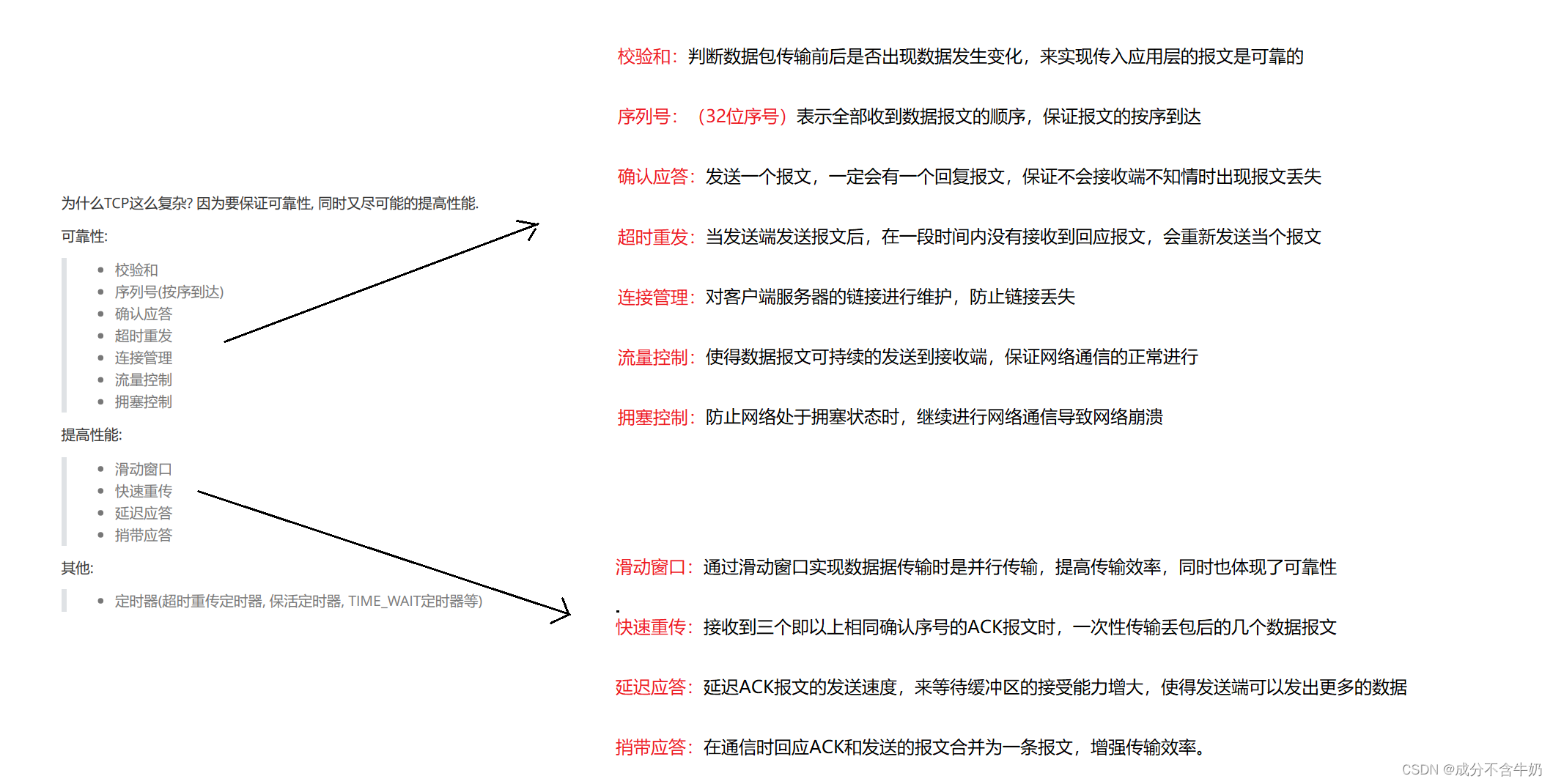
Linux网络编程：传输层协议|UDP|TCP
知识引入： 端口号： 当应用层获得一个传输过来的报文时，这时数据包需要知道，自己应该送往哪一个应用层的服务，这时就引入了“端口号”，通过区分同一台主机不同应用程序的端口号，来保证数据传输…...
MongoDB CRUD操作：内嵌文档查询
MongoDB内嵌文档的查询 文章目录 MongoDB内嵌文档的查询使用点号.查询内嵌文档嵌套字段的相等匹配使用查询操作符进行匹配指定AND条件 嵌套文档的匹配使用 MongoDB Atlas 查询内嵌文档导航至集合指定查询过滤文档点击应用 可以使用下面几种方法查询MongoDB中的嵌入文档…...
JavaScript、Kotlin、Flutter可以开发鸿蒙APP吗？
自从去年华为宣布推出「鸿蒙Next」版本开始，标志着其操作系统的全面革新。鸿蒙Next将摒弃所有基于AOSP的代码，与Android系统彻底分离，实现完全自主的研发路径。通过精简约40%的冗余代码，鸿蒙Next致力于构建一个更高效、更流畅的系…...
刚体运动描述：欧拉角与四元数
在机器人学中，刚体的运动描述是非常重要的，特别是当我们需要精确控制机器人的姿态时。欧拉角和四元数是两种常用的描述刚体在三维空间中旋转的方法。下面将分别介绍这两种方法并给出其特点。 欧拉角 定义与特点： 定义：欧拉角是…...
一文速通23种设计模式——单例模式、工厂模式、建造者模式、原型模式、代理模式、装饰器模式、组合模式、组合模式、桥接模式、观察者模式、策略模式……
一文速通23种设计模式 写在前面 本文基于结城浩所著《图解设计模式》，其中所使用代码皆为Java版本。 随书代码下载地址-点击“随书下载” 全文15205字，全部读完需要约20分钟。 目录 一文速通23种设计模式写在前面 第一部分 适应设计模式迭代器模式 (…...
Lua 基础 04 模块
Lua 基础相关知识 第四期 require 模块，通常是一个表，表里存储了一些字段和函数，单独写在一个 lua 文件。 例如，这是一个 tools.lua 文件，定义了一个局部 tools 表，包含一个 log 函数，可以传…...
速递FineWeb：一个拥有无限潜力的15T Tokens的开源数据集
大模型技术论文不断，每个月总会新增上千篇。本专栏精选论文重点解读，主题还是围绕着行业实践和工程量产。若在某个环节出现卡点，可以回到大模型必备腔调或者LLM背后的基础模型新阅读。而最新科技（Mamba,xLSTM,KAN）则提…...
HDLBits答案汇总
一.Getting Started Getting started-CSDN博客 二.Verilog Basics-CSDN博客 Vectors-CSDN博客 Module Hierarchy-CSDN博客 Procedures-CSDN博客 More Verilog Features-CSDN博客 三.Circuits Combinational Basic-CSDN博客 Multiplexers-CSDN博客 Arithmetic-CSDN博客 Karnau…...
云端数据提取：安全、高效地利用无限资源
在当今的大数据时代，企业和组织越来越依赖于云平台存储和处理海量数据。然而，随着数据的指数级增长，数据的安全性和高效的数据处理成为了企业最为关心的议题之一。本文将探讨云端数据安全的重要性，并提出一套既高效又安全的数据提…...
Java开发：Spring Boot 实战教程
序言 随着技术的快速发展和数字化转型的深入推进，软件开发领域迎来了前所未有的变革。在众多开发框架中，Spring Boot凭借其“约定大于配置”的核心理念和快速开发的能力，迅速崭露头角，成为当今企业级应用开发的首选框架之一。 《…...
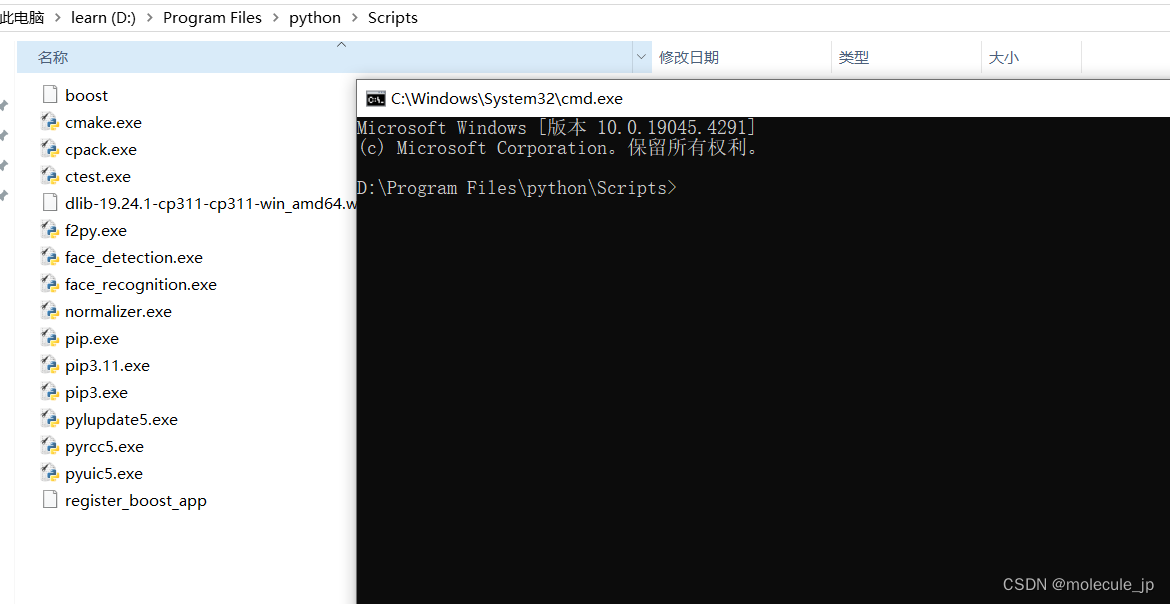
【Python3.11版本利用whl文件安装对应的dlib-19.24.1-cp311-cp311-win_amd64.whl库】
下载Python对应的安装包 找到自己Python版本对应的dlib whl库将网盘下载好的文件放在安装Python的Scripts路径下面接着在该路径输入cmdpip进行安装使用的是国内的源 找到自己Python版本对应的dlib whl库 python 3.11 对应 dlib-19.24.1-cp311-cp311-win_amd64.whl -i 也可以去…...
HW面试常见知识点2——研判分析（蓝队中级版）
🍀文章简介：又到了一年一度的HW时刻，本文写给新手想快速进阶HW蓝中的网安爱好者们， 通读熟练掌握本文面试定个蓝中还是没问题的！大家也要灵活随机应变，不要太刻板的回答） 🍁个人主页…...
鲁教版七年级数学下册-笔记
文章目录 第七章 二元一次方程组1 二元一次方程组2 解二元一次方程组3 二元一次方程组的应用4 二元一次方程与一次函数5 三元一次方程组 第八章 平行线的有关证明1 定义与命题2 证明的必要性3 基本事实与定理4 平行线的判定定理5 平行限的性质定理6 三角形内角和定理 第九章 概…...
带你走进在线直线度测量仪 解析测量方法！
在线直线度测量仪 在线直线度测量仪可安装于生产线上，进行非接触式的无损检测，能检测米直线度尺寸，对截面为圆形的产品，进性直线度检测的帮手。 测量方法 在线直线度拟采用我公司的光电测头对矫直后的棒材直线度进行测量。测量时…...
力扣1 两数之和
给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。 你可以按任意顺序返回…...
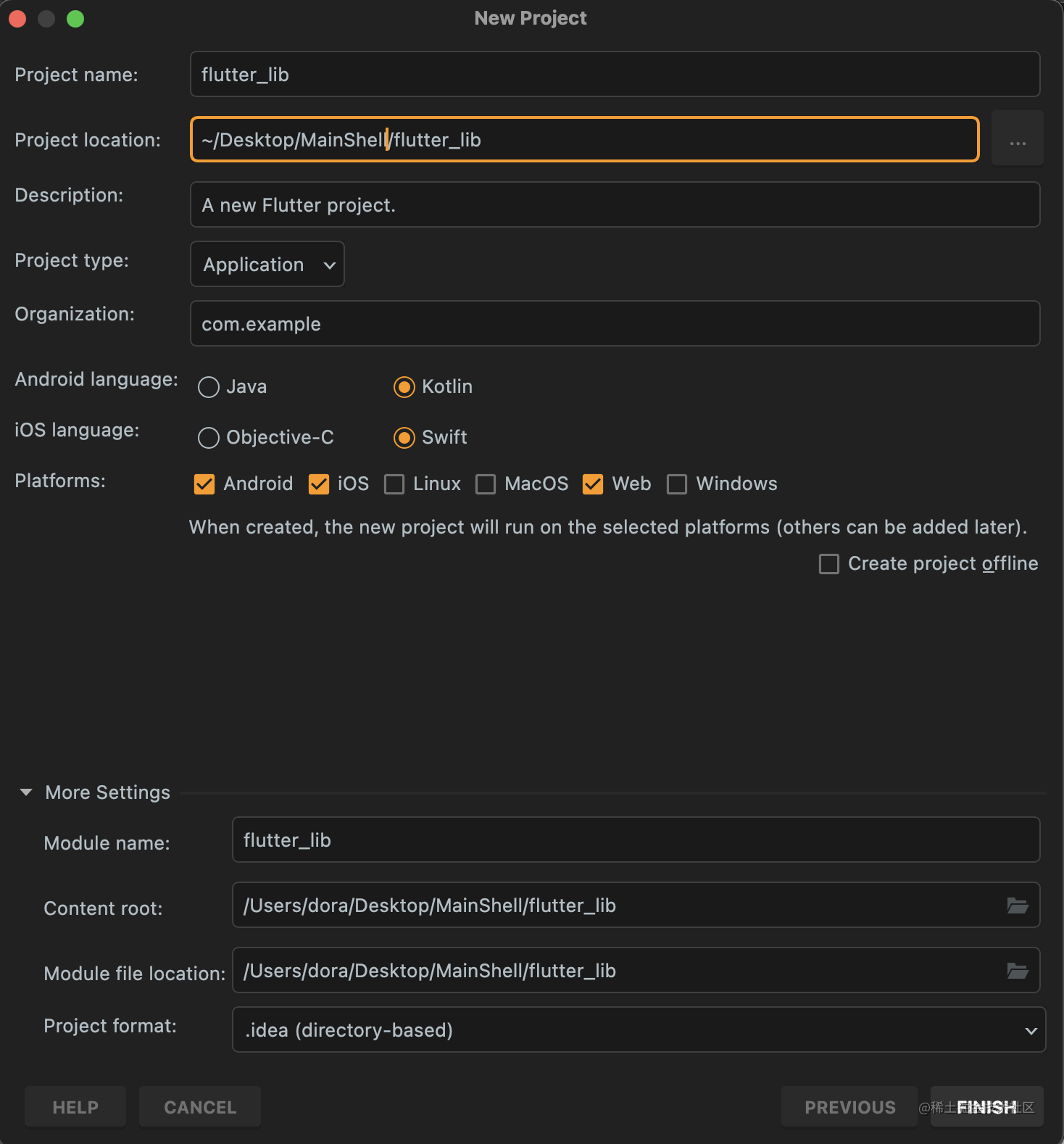
AndroidFlutter混合开发
为什么要有混合开发 我们知道，Flutter是可以做跨平台开发的，即一份Flutter的Dart代码，可以编译到多个平台上运行。这么做的好处就是，在不降低多少性能的情况下，尽最大可能的节省开发的时间成本，直接将开发…...
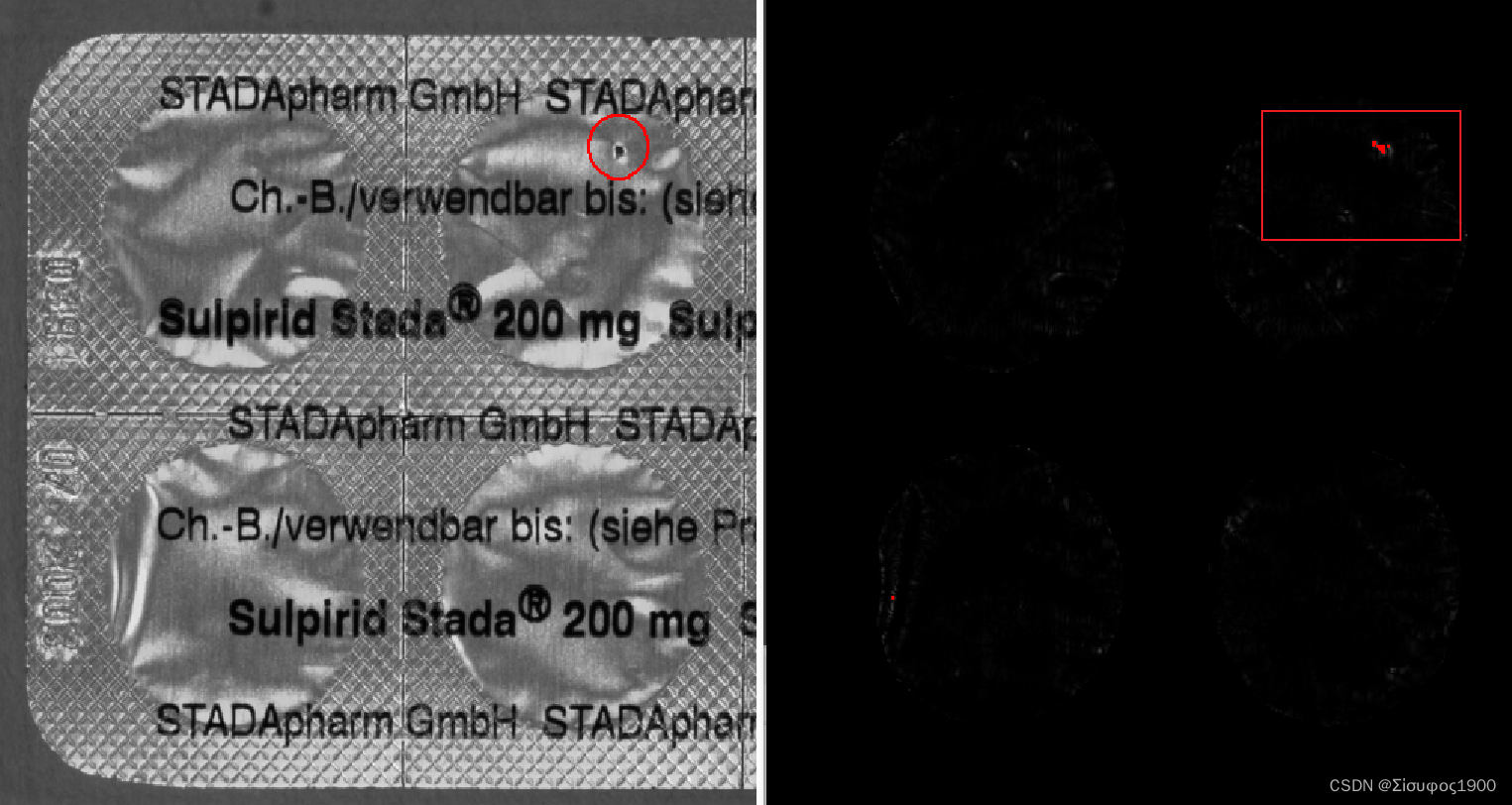
Halcon 光度立体 缺陷检测
一、概述 halcon——缺陷检测常用方法总结（光度立体） - 唯有自己强大 - 博客园 (cnblogs.com) 上周去了康耐视的新品发布会，我真的感觉压力山大，因为VM可以实现现在项目中的80% 的功能，感觉自己的不久就要失业了。同时…...
关于找暑期实习后的一些反思
日期 2024年6月3日 写在前面：距离研究生毕业还有9个月，前端时间一直在不停地投简历，不停地刷笔试题，不停地被拒绝，今天悬着的心终于死透了，心情还是比较糟糕的，可能唯一的安慰就是一篇小论文终于…...
深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架，用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录，以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...
基础测试工具使用经验
背景 vtune，perf, nsight system等基础测试工具，都是用过的，但是没有记录，都逐渐忘了。所以写这篇博客总结记录一下，只要以后发现新的用法，就记得来编辑补充一下 perf 比较基础的用法： 先改这…...
Neo4j 集群管理：原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档，本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石，用于构建高可用、可扩展且一致的图数据库服务…...
Python爬虫（一）：爬虫伪装
一、网站防爬机制概述 在当今互联网环境中，具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类： 身份验证机制：直接将未经授权的爬虫阻挡在外反爬技术体系：通过各种技术手段增加爬虫获取数据的难度…...
uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 （部分有免费额度&#x…...
数据库分批入库
今天在工作中，遇到一个问题，就是分批查询的时候，由于批次过大导致出现了一些问题，一下是问题描述和解决方案： 示例： // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
css3笔记 （1） 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size：0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
Device Mapper 机制
Device Mapper 机制详解 Device Mapper（简称 DM）是 Linux 内核中的一套通用块设备映射框架，为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程，并配以详细的…...
力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...