代码随想录第23天|回溯part3 组合与分割
39.组合总和

class Solution {
public:vector<vector<int>> res;vector<int> path;void backTracking(vector<int>& candidates,int target,int sum,int n,int step){if(n > 150) return;if(sum > target) return;if(sum == target){res.push_back(path);return;}for(int i = step; i < candidates.size(); i++){path.push_back(candidates[i]);backTracking(candidates,target,sum+candidates[i],n+1,i);path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backTracking(candidates,target,0,0,0);return res;}
};40.组合总和2
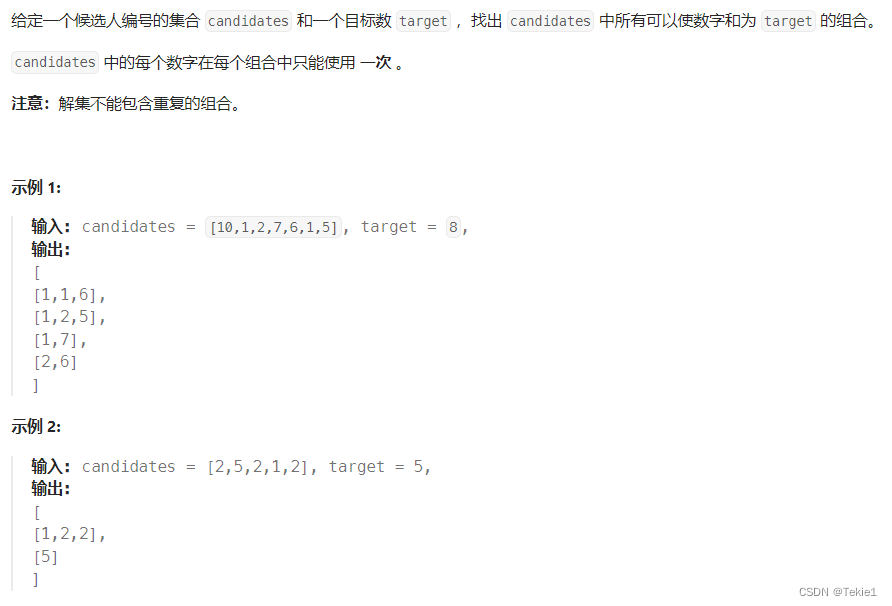
难题

可以看出在candidates[i] == candidates[i - 1]相同的情况下:
used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
used[i - 1] == false,说明同一树层candidates[i - 1]使用过
因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上
即:因为在排序后,相同的数都会挨在一起,如果当前数和上个数相同的话,那么在递归的过程中,如果上一个数没被用到,那么当前数肯定是一种重复的情况,因为这两个数相同,肯定是先使用前一个数的,而如果上一个没用到,则表示是已经递归过上一个数的所有情况并回溯了,现在递归下一个数的,所以需要跳过重复的这个数。
class Solution {
public:vector<vector<int>> res;vector<int> path;bool used[101];void backTracking(vector<int>& candidates, int target, int sum, int step) {if (sum == target) {res.push_back(path);return;}for (int i = step; i < candidates.size(); i++) {if (sum + candidates[i] > target)break;if (i > 0 && used[i - 1] == false &&candidates[i] == candidates[i - 1])continue;path.push_back(candidates[i]);used[i] = true;backTracking(candidates, target, sum + candidates[i], i + 1);used[i] = false;path.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());backTracking(candidates, target, 0, 0);return res;}
};
也可以直接使用startIndex来去重,每层递归里,如果一个数和上一个数相同,则跳过
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// 要对同一树层使用过的元素进行跳过// 这里i > startIndex是为了确保可以选取到同一种元素,在下层递归的时候,因为传入的是i+1,所以如果i+1和上一个元素相同,递归后也可以选取和i相同的元素if (i > startIndex && candidates[i] == candidates[i - 1]) {continue;}sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i + 1); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次sum -= candidates[i];path.pop_back();}}
131.分割回文串

回溯三步
1.递归函数确定参数:string s, int step
2.确定终止条件:因为分割串类似于组合问题,
例如对于字符串abcdef:
组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个…。
切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段…。

返回条件就是,当切割点超过串的长度时,说明已经找到一种每个字串都是回文串的方案了,这个时候就可以把字串数组传给结果
3.确定单层逻辑
单层逻辑就是树的横向遍历,即用for循环确定切割点,且切割点必须不断往后
class Solution {
public:vector<vector<string>> res;vector<string> path;bool check(string t) {for (int i = 0, j = t.size() - 1; i < j; i++, j--) {if (t[i] != t[j])return false;}return true;}void backTracking(string s, int step) {if (step >= s.size()) {// 如果大于数组长度,则找到一组全为回文串的字串组合,否则被continue掉了res.push_back(path);return;}for (int i = step; i < s.size(); i++) {// 截取字串string t = s.substr(step, i - step + 1);// 找到了符合条件的字串if (check(t))path.push_back(t);elsecontinue;// 进行下一层递归backTracking(s, i + 1);path.pop_back();}}vector<vector<string>> partition(string s) {backTracking(s, 0);return res;}
};
最近在学go,所以提供一个go版本的代码
var res [][]string
var path []stringfunc check(t string) bool {for i, j := 0, len(t)-1; i < j; i, j = i+1, j-1 {if t[i] != t[j] {return false}}return true
}
func backTracking(s string, step int) {if step >= len(s) {temp := make([]string, len(path))copy(temp, path)res = append(res, temp)return}for i := step; i < len(s); i++ {t := s[step : i+1]if check(t) {path = append(path, t)} else {continue}backTracking(s, i+1)path = path[:len(path)-1]}
}
func partition(s string) [][]string {path = make([]string, 0)res = make([][]string, 0)backTracking(s, 0)return res
}
相关文章:

代码随想录第23天|回溯part3 组合与分割
39.组合总和 class Solution { public:vector<vector<int>> res;vector<int> path;void backTracking(vector<int>& candidates,int target,int sum,int n,int step){if(n > 150) return;if(sum > target) return;if(sum target){res.push_…...

nginx和proxy_protocol协议
目录 1. 引言2. HTTP server的配置3. Stream server的配置3.1 作为proxy_protocol的前端服务器3.2 作为proxy_protocol的后端服务器1. 引言 proxy_protocol 是haproxy开发的一种用于在代理服务器和后端服务器之间传递客户端连接信息的协议。使用 proxy_protocol 的主要优势是能…...

【pytorch】数据转换/增强后保存
数据转换 from PIL import Image from pathlib import Path import matplotlib.pyplot as plt import numpy as npimport torch import torchvision.transforms as Tplt.rcParams["savefig.bbox"] = tight # orig_im...
超越Devin!姚班带队,他们创大模型编程新世界纪录
超越Devin!SWEBench排行榜上迎来了新玩家—— StarShip CodeGen Agent,姚班带队初创公司OpenCSG出品,以23.67%的成绩获得全球第二名的成绩。 同时创造了非GPT-4o基模的最高纪录(SOTA)。 我们都知道,SWEBe…...

江苏大信环境科技有限公司:环保领域的开拓者与引领者
2009 年,江苏大信环境科技有限公司在宜兴环保科技工业园成立。自创立之始,该公司便笃定坚守“诚信为本、以质量求生存、以创新谋发展”这一经营理念,全力以赴为客户构建专业的工业有机废气治理整体解决方案,进而成为国家高新技术企…...

关于 Bean 容器的注入方式,99 % 的人都答不全!
引言:在使用 Spring 框架开发应用程序时,依赖注入是一个至关重要的概念。而对于 Bean 容器的注入方式,虽然我们可能都有一定的了解,但实际上很多人在被问及这个问题时可能并不能完整地回答。本文将深入探讨 Spring 中 Bean 容器的…...

Spring的@Async注解及其用途
Spring 的 Async 注解是 Spring Framework 4.2 版本引入的功能,它用于支持异步方法执行。当一个方法标注了 Async,Spring 会在一个单独的线程中调用该方法,从而不会阻塞主线程的执行。 Async 注解的用途: 提高性能:通…...
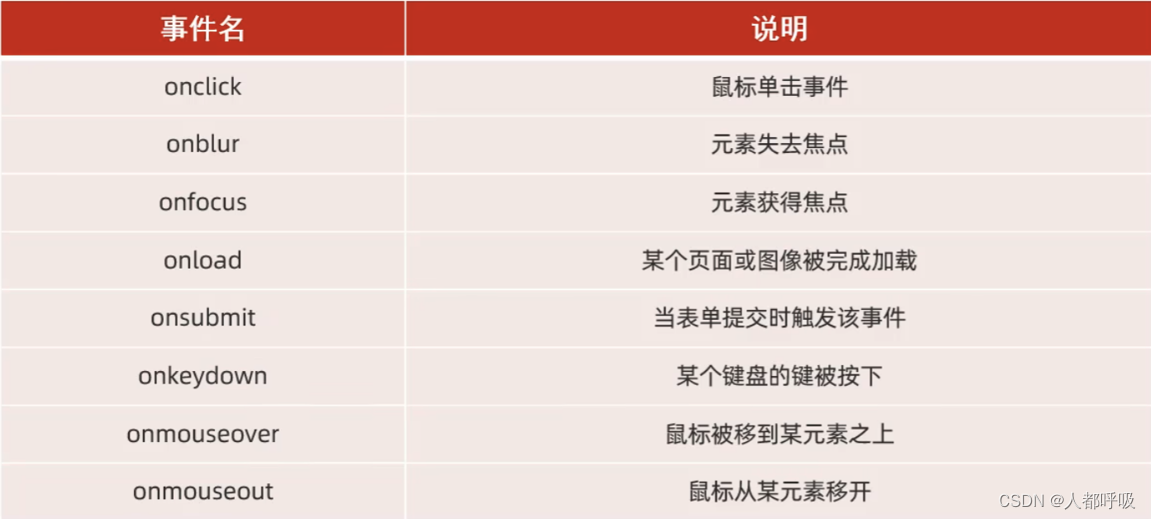
JS(DOM、事件)
DOM 概念:Document Object Model,文档对象模型。将标记语言的各个组成部分封装为对应的对象: Document:整个文档对象Element:元素对象Attribute:属性对象Text:文本对象Comment:注释对象 JavaScript通过DOM,就能够对HTML进行操作: 改变 HTML 元素的内…...

学习小心意——python的构造方法和析构方法
构造方法和析构方法分别用于初始化对象的属性和释放类占有的资源 构造方法_init_() 语法格式如下: class 类名:def __init__(self, 参数1, 参数2, ...):# 初始化代码self.属性1 参数1self.属性2 参数2# ... 示例代码如下 class Student:def __init__(self):s…...

GB/T 23995-2009 室内装饰装修用溶剂型醇酸木器涂料检测
溶剂型醇酸木器涂料是指以醇酸树脂为主要成膜物,通过氧化干燥成膜的溶剂型木器涂料适用于室内木制品表面的保护及装饰。 GB/T 23995-2009室内装饰装修用溶剂型醇酸木器涂料检测项目: 测试指标 测试方法 在容器中状态 GB/T 23995 细度 GB/T 6753.1 …...
Maven 中的 classifier 属性用过没?
最近训练营有小伙伴问到松哥一个关于 Maven 依赖的问题,涉及到 classifier 属性,随机问了几个小伙伴,都说工作中没用到过,因此简单整篇文章和小伙伴们分享下。 Maven 大家日常开发应该都有使用,Maven 中有一个比较好玩…...
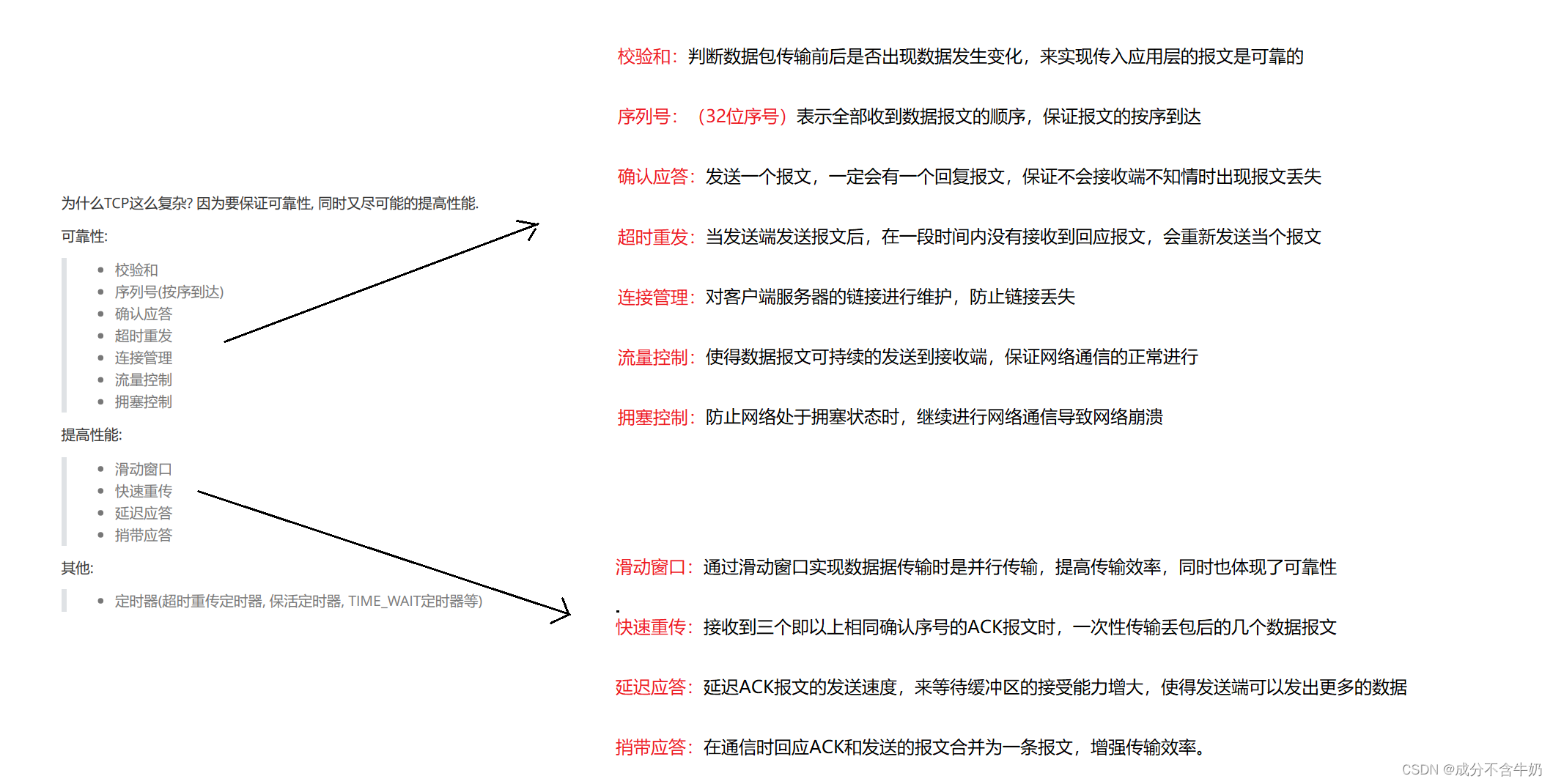
Linux网络编程:传输层协议|UDP|TCP
知识引入: 端口号: 当应用层获得一个传输过来的报文时,这时数据包需要知道,自己应该送往哪一个应用层的服务,这时就引入了“端口号”,通过区分同一台主机不同应用程序的端口号,来保证数据传输…...

MongoDB CRUD操作:内嵌文档查询
MongoDB内嵌文档的查询 文章目录 MongoDB内嵌文档的查询使用点号.查询内嵌文档嵌套字段的相等匹配使用查询操作符进行匹配指定AND条件 嵌套文档的匹配使用 MongoDB Atlas 查询内嵌文档导航至集合指定查询过滤文档点击应用 可以使用下面几种方法查询MongoDB中的嵌入文档…...

JavaScript、Kotlin、Flutter可以开发鸿蒙APP吗?
自从去年华为宣布推出「鸿蒙Next」版本开始,标志着其操作系统的全面革新。鸿蒙Next将摒弃所有基于AOSP的代码,与Android系统彻底分离,实现完全自主的研发路径。通过精简约40%的冗余代码,鸿蒙Next致力于构建一个更高效、更流畅的系…...

刚体运动描述:欧拉角与四元数
在机器人学中,刚体的运动描述是非常重要的,特别是当我们需要精确控制机器人的姿态时。欧拉角和四元数是两种常用的描述刚体在三维空间中旋转的方法。下面将分别介绍这两种方法并给出其特点。 欧拉角 定义与特点: 定义:欧拉角是…...

一文速通23种设计模式——单例模式、工厂模式、建造者模式、原型模式、代理模式、装饰器模式、组合模式、组合模式、桥接模式、观察者模式、策略模式……
一文速通23种设计模式 写在前面 本文基于结城浩所著《图解设计模式》,其中所使用代码皆为Java版本。 随书代码下载地址-点击“随书下载” 全文15205字,全部读完需要约20分钟。 目录 一文速通23种设计模式写在前面 第一部分 适应设计模式迭代器模式 (…...

Lua 基础 04 模块
Lua 基础相关知识 第四期 require 模块,通常是一个表,表里存储了一些字段和函数,单独写在一个 lua 文件。 例如,这是一个 tools.lua 文件,定义了一个局部 tools 表,包含一个 log 函数,可以传…...

速递FineWeb:一个拥有无限潜力的15T Tokens的开源数据集
大模型技术论文不断,每个月总会新增上千篇。本专栏精选论文重点解读,主题还是围绕着行业实践和工程量产。若在某个环节出现卡点,可以回到大模型必备腔调或者LLM背后的基础模型新阅读。而最新科技(Mamba,xLSTM,KAN)则提…...

HDLBits答案汇总
一.Getting Started Getting started-CSDN博客 二.Verilog Basics-CSDN博客 Vectors-CSDN博客 Module Hierarchy-CSDN博客 Procedures-CSDN博客 More Verilog Features-CSDN博客 三.Circuits Combinational Basic-CSDN博客 Multiplexers-CSDN博客 Arithmetic-CSDN博客 Karnau…...

云端数据提取:安全、高效地利用无限资源
在当今的大数据时代,企业和组织越来越依赖于云平台存储和处理海量数据。然而,随着数据的指数级增长,数据的安全性和高效的数据处理成为了企业最为关心的议题之一。本文将探讨云端数据安全的重要性,并提出一套既高效又安全的数据提…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...
