【数据结构】从前序与中序遍历,或中序与后序遍历序列,构造二叉树
欢迎浏览高耳机的博客
希望我们彼此都有更好的收获
感谢三连支持!


首先,根据先序遍历可以确定根节点E,再在中序遍历中通过E确定左树和右数 ;
设立inBegin和inEnd,通过这两个参数的游走,来进行子树的创建;
已知根节点,则左子树的范围表示为(inBegin,rootIndex - 1);
而右子树为(rootIndex + 1,inEnd);
通过递归调用,即可不断创建子树,直到叶子节点;
如果inBegin > inEnd,则说明此时为叶子节点,应该返回上一层递归;
public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeChilde(preorder, inorder, 0, inorder.length-1);
}private TreeNode buildTreeChilde(int[] preorder, int[] inorder, int inBegin, int inEnd) {if(inBegin > inEnd){return null;}TreeNode root = new TreeNode(preorder[preIndex]); // 创建根节点int rootIndex = findRootIndex(inorder, inBegin, inEnd, preorder[preIndex]); // 找到根节点在中序遍历中的位置preIndex++;root.left = buildTreeChilde(preorder, inorder, inBegin, rootIndex-1); // 递归构建左子树root.right = buildTreeChilde(preorder, inorder, rootIndex+1, inEnd); // 递归构建右子树return root;
}private int findRootIndex(int[] inorder, int inBegin, int inEnd, int key){for (int i = inBegin; i <= inEnd; i++) {if (key == inorder[i]) {return i;}}return -1;}OJ链接:
https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/
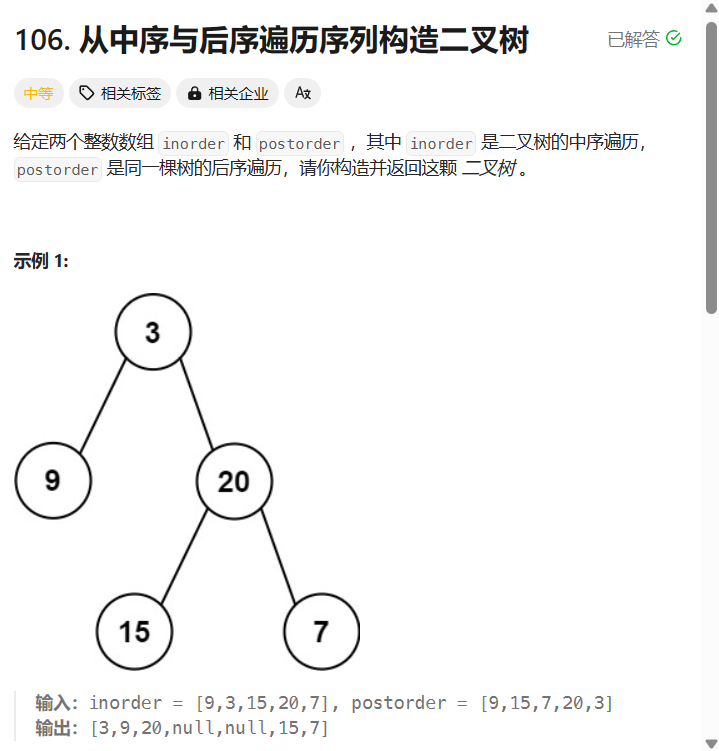

同样的,根据后序遍历可以确定根节点,再在中序遍历中通过根节点确定左树和右数 ;
需要注意的是,由于postIndex根据后序遍历(左,右,根)创建,与前序遍历相反,所以每次递归时postIndex--,从根节点前的右子树开始递归;
同样的,已知根节点,则右子树表示范围为(rootIndex + 1,inEnd);
而左子树表示为(inBegin,rootIndex - 1);
通过递归调用,即可不断创建子树,直到叶子节点;
如果inBegin > inEnd,则说明此时为叶子节点,应该返回上一层递归;
public TreeNode buildTree(int[] inorder, int[] postorder) {postIndex = postorder.length-1;return buildTreeChilde(inorder, postorder, 0, inorder.length-1);
}private TreeNode buildTreeChilde(int[] inorder, int[] postorder, int inBegin, int inEnd) {if(inBegin > inEnd){return null;}TreeNode root = new TreeNode(postorder[postIndex]); // 创建根节点int rootIndex = findRootIndex(inorder, inBegin, inEnd, postorder[postIndex]); // 找到根节点在中序遍历中的位置postIndex--;root.right = buildTreeChilde(inorder, postorder, rootIndex+1, inEnd); // 递归构建右子树root.left = buildTreeChilde(inorder, postorder, inBegin, rootIndex-1); // 递归构建左子树return root;
}private int findRootIndex(int[] inorder, int inBegin, int inEnd, int key){for (int i = inBegin; i <= inEnd; i++) {if (key == inorder[i]) {return i;}}return -1;}OJ链接:https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/
希望这篇博客能为你理解java编程思想提供一些帮助。
如有不足之处请多多指出。
我是高耳机。
相关文章:

【数据结构】从前序与中序遍历,或中序与后序遍历序列,构造二叉树
欢迎浏览高耳机的博客 希望我们彼此都有更好的收获 感谢三连支持! 首先,根据先序遍历可以确定根节点E,再在中序遍历中通过E确定左树和右数 ; 设立inBegin和inEnd,通过这两个参数的游走,来进行子树的创建&a…...

ARM公司发展历程
Arm从1990年成立前开始,历经漫长岁月树立各项公司里程碑及产品成就,一步步成为全球最普及的运算平台。 添加图片注释,不超过 140 字(可选) Acorn 时期 1978年,Chris Curry和Hermann Hauser共同创立了Acorn…...

C# :IQueryable IEnumerable
文章目录 1. IEnumerable2. IQueryable3. LINQ to SQL4. IEnumerable & IQueryable4.1 Expression4.2 Provider 1. IEnumerable namespace System.Collections: public interface IEnumerable {public IEnumerator GetEnumerator (); }public interface IEnumerator {pubi…...

三、生成RPM包
文章目录 1、编译生成so、bin 通过此工程编译生成so\bin文件 2、将so\bin打包到rpm中 ###### 1.生成可执行文件、库文件 ######### cmake_minimum_required(VERSION 3.15)project(compute) set(target zls_bin) set(target2 libcompute.so) # 依赖的头文件 include_directori…...

单实例11.2.0.4迁移到11.2.0.4RAC_使用rman异机恢复
保命法则:先备份再操作,磁盘空间紧张无法备份就让满足,给自己留退路。 场景说明: 1.本文档的环境为同平台、不同版本(操作系统版本可以不同,数据库版本相同),源机器和目标机器部分…...
)
MySQL之查询性能优化(二)
查询性能优化 慢查询基础:优化数据访问 查询性能低下最基本的原因是访问的数据太多。某些查询可能不可避免地需要筛选大量数据,但这并不场景。大部分性能低下的查询都可以通过减少访问的数据量的方式进行优化。对于低效的查询,我们发现通过下面两个步骤…...

The Best Toolkit 最好用的工具集
The Best Toolkit 工欲善其事,必先利其器,整理过往工作与生活中遇到的最好的工具软件 PDF合并等 PDF24 Tools PDF查看器 SumatraPDF 可以使用黑色来查看,相对不伤眼睛,也有电子书相关的阅读器 Kindle pdf裁边工具 briss 软件卸载…...
类型)
使用C#反射中的MAKEGENERICTYPE函数,来为泛型方法和泛型类指定(泛型的)类型
MakeGenericType 是一个在 C# 中用于创建开放类型的实例的方法。开放类型是一种未绑定类型参数的泛型类型。当你有一个泛型类型定义,并且想要用特定的类型实例化它时,你可以使用 MakeGenericType 方法。 public Type MakeGenericType (params Type[] ty…...

sql注入 (运用sqlmap解题)
注:level参数 使用–batch参数可指定payload测试复杂等级。共有五个级别,从1-5,默认值为1。等级越高,测试的payload越复杂,当使用默认等级注入不出来时,可以尝试使用–level来提高测试等级。 --level 参数决定了 sql…...

HTML5 Canvas 绘图教程二
在本教程中,我们将探讨 canvas 的高级用法,包括复杂的绘图 API、坐标系统和变换操作、平滑动画技术以及复杂应用和游戏开发的实践。 1. 绘图 API 高级方法 1.1 二次贝塞尔曲线 (quadraticCurveTo) 二次贝塞尔曲线需要两个点:一个控制点和一…...

Linux 命令 find 的深度解析与使用
Linux 命令 find 的深度解析与使用 在 Linux 系统中,find 命令是一个功能强大的工具,用于在文件系统中搜索文件或目录。无论是基于文件名、文件类型、文件大小、文件权限,还是基于文件的最后修改时间等,find 命令都能提供灵活的搜…...

字符串操作记录
1 拼接 Concat():拼接字符串 Let stringvalue “hello ”; Let result stringvalue.concat(“world”) Console.log(result) // “hello world” 2 删 Let stringvalue “hello world”Console.log(stringvalue.slice(3)); // ‘lo world’Console.log(stringvalue.subst…...

【python科学文献计量】关于中国知网检索策略的验证,以事故伤害严重程度检索为例
关于中国知网检索策略的验证,以事故伤害严重程度检索为例 1 背景2 文献下载3 数据处理1 背景 由于要进行相关研究内容的综述,需要了解当前我国对于事故伤害严重程度的研究现状,采用国内较为知名的检索网站(中国知网)进行文献数据集检索 由于最近知网出bug,检索的结果在…...

AdminController
目录 1、 AdminController 1.1、 UpdateFaculty 1.1.1、 // Check if a new image file is provided 1.1.2、 // CHECKING FOLDER EXIST OR NOT - IF NOT THEN CREATE F0LDER 1.1.3、 // READY SEND PATH TO IMAGE TO DB 1.1.4、 DeleteFaculty 1.1.5、 // If th…...

Vue3-Pinia状态管理器
Pinia 是 Vue 的专属状态管理库,它允许你跨组件或页面共享状态。如果你熟悉组合式 API 的话,你可能会认为可以通过一行简单的 export const state reactive({}) 来共享一个全局状态。对于单页应用来说确实可以,但如果应用在服务器端渲染&…...

安装存储器的段描述符并加载GDTR
代码清单 ;代码清单12-1;文件名:c12_mbr.asm;文件说明:硬盘主引导扇区代码;创建日期:2011-5-16 19:54;修改于2022-02-16 11:15;设置堆栈段和栈指针mov ax, csmov ss, axmov sp, 0x7c00;计算GDT所在的逻辑段地址12 mov ax, [c…...

2024年5月架构试题
2024年5月份架构师考试真题完整版 截至2024-5-28 19:24:14已全部收录完成 共75道选择题,5道案例题,4道论文题。题目顺序不分先后。 全网最全的2024年5月份架构师考试真题回忆版,包含答案和解析。 选择题 计算机基础 操作系统调度算法 选先来先…...

品牌控价的同时也要做好数据分析
品牌在进行电商价格监测时,确实不应仅停留在收集低价数据的层面。在数据量巨大的今天,如何深度分析和挖掘这些数据的价值,为品牌的决策和战略提供有力支持,显得尤为重要。 首先,电商数据的监测和分析有助于品牌更全面…...
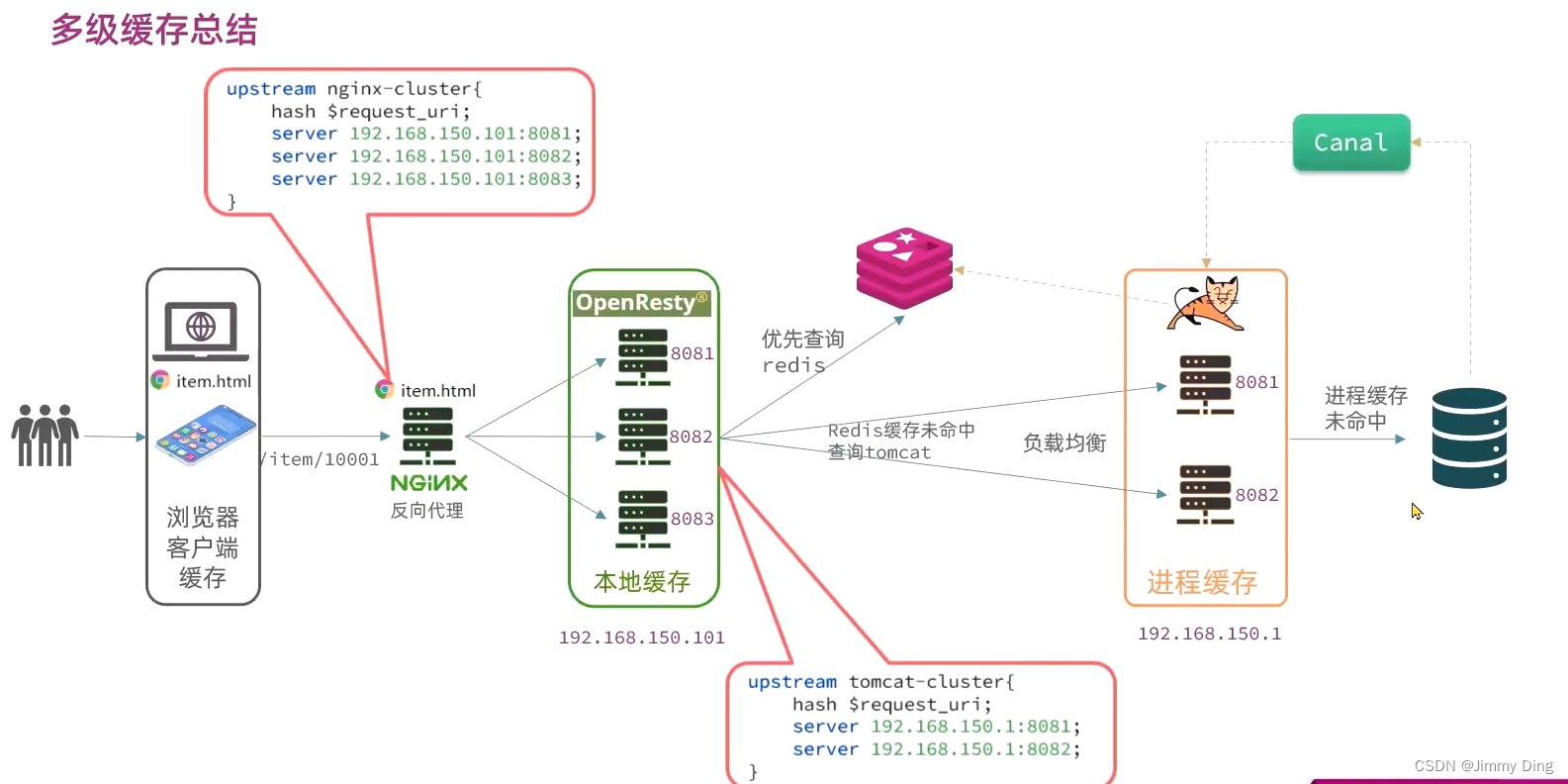
微服务学习Day11-缓存问题学习
文章目录 多级缓存引入JVM进程缓存导入商品案例Caffeine学习实现进程缓存 Lua语法入门认识Lua变量和循环条件控制、函数 多级缓存安装OpenRestyOpenResty入门请求参数处理查询TomcatRedis缓存预热查询Redis缓存Nginx本地缓存 缓存同步策略策略安装Canal监听Canal 多级缓存引入 …...

虚拟化知识学习
虚拟化知识学习 关键概念和术语的简要介绍 虚拟化的基本概念 虚拟机 (VM):一个虚拟机是一个模拟计算机系统的环境。它运行在物理硬件之上,但与物理硬件隔离,提供类似于物理计算机的功能。 虚拟化技术:这是指使用软件来创建虚拟版…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

