HTML旋转照片盒子
效果图
<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><meta http-equiv="X-UA-Compatible" content="ie=edge"><title>旋转小方块</title><link rel="stylesheet" href="css.css">
</head>
<body><div class="wrapper"><div class="item1"></div><div class="move1"><img src="img/1.png" alt=""></div><div class="item2"></div><div class="move2"><img src="img/2.png" alt=""></div><div class="item3"></div><div class="move3"><img src="img/3.png" alt=""></div><div class="item4"></div><div class="move4"><img src="img/4.png" alt=""></div><div class="item5"></div><div class="move5"><img src="img/5.png" alt=""></div><div class="item6"></div><div class="move6"><img src="img/6.png" alt=""></div></div><script>var wra = document.getElementsByClassName('wrapper')[0];var move1 = document.getElementsByClassName('move1')[0];var move2 = document.getElementsByClassName('move2')[0];var move3 = document.getElementsByClassName('move3')[0];var move4 = document.getElementsByClassName('move4')[0];var move5 = document.getElementsByClassName('move5')[0];var move6 = document.getElementsByClassName('move6')[0];console.log(move5);var key = true;wra.onmouseenter = function(e){// wra.style.animationPlayState = 'paused';move1.style.animation = 'move1 2s linear infinite';move2.style.animation = 'move2 2s linear infinite';move3.style.animation = 'move3 2s linear infinite';move4.style.animation = 'move4 2s linear infinite';move5.style.animation = 'move5 2s linear infinite';move6.style.animation = 'move6 2s linear infinite';}wra.onmouseleave = function(e){// wra.style.animationPlayState = 'paused';move1.style.animation = '';move2.style.animation = '';move3.style.animation = '';move4.style.animation = '';move5.style.animation = '';move6.style.animation = '';}</script>
</body>
</html>CSS样式代码私聊有偿获取昂
相关文章：
HTML旋转照片盒子
效果图 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv"X-UA-Compatible" content…...
【UE5 刺客信条动态地面复刻】实现无界地面01：动态生成
2024.6.4更新 昨天半夜意识到生成Cube的方案不合适，又开始到处找动态地面的方法，发现了我想要的效果直接可以用nigara实现！！！！ 于是这个部分就暂时告一段落，今季开始新的方向的学习。 为了快速…...
AI产品经理系列-如何使用kimi快速撰写用户故事(含提示词)
在AI时代，可能人人都可成为产品经理。 之前我们聊过如何使用kimi协助完成产品需求文档，如何写竞品分析报告，这一篇我们聊聊用户故事，如何使用kimi协助撰写产品需求文档中的用户故事。 在此之前我们先了解下什么是用户故事&#…...
MySQL索引与事务
前言👀~ 紧接着数据库的相关知识，今天讲解MySQL面试中频繁被问到的知识点，索引与事务!!! 如果各位对文章的内容感兴趣的话，请点点小赞，关注一手不迷路，如果内容有什么问题的话，欢迎各位评论纠正…...
『大模型笔记』从基础原理出发提升深度学习性能
从基础原理出发提升深度学习性能 文章目录 一. 从基础原理出发提升深度学习性能1.1. 计算（compute）1.2. 带宽（Bandwidth）1.2.1 关于内存带宽成本的推理(Reasoning about Memory-Bandwidth Costs)1.3. 开销（Overhead）二. 总结三. 参考文献Making Deep Learning Go Brrrr F…...
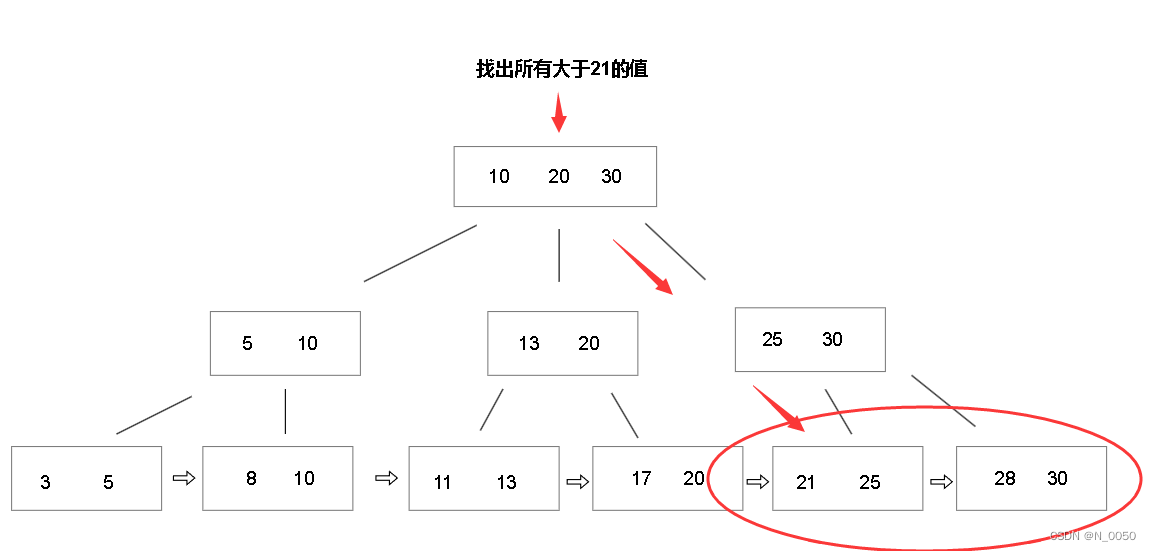
【二叉树】Leetcode 222. 完全二叉树的节点个数【简单】
完全二叉树的节点个数 你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。 完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最…...
golang界面设计器，全网少见
今天登录govcl的网站，无意中看到有个简易UI设计器。 对于golang的UI专用设计器，还没在网上真正见过。 之前也用govcl来做过两三个桌面应用，好用是好用，不过要安装Lazarus的IDE来拖动设计UI，还要配置很多东西࿰…...
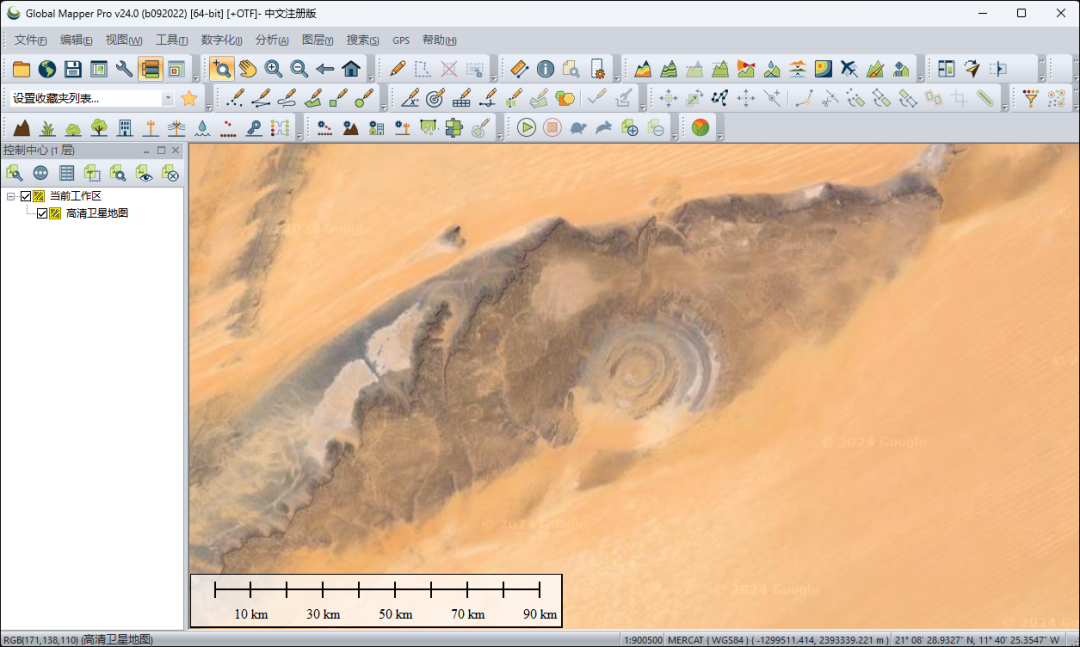
如何在GlobalMapper中加载高清卫星影像？
GlobalMapper在GIS行业几乎无人不知，无人不晓，但它可以直接加载卫星影像也许就不是每个人都知道的了。 这里就来分享一下如何在GlobalMapper中加载高清卫星影像，并可以在文末查看领取软件安装包和图源的方法。 如何加载高清图源 首先&…...
【机器学习】解锁AI密码：神经网络算法详解与前沿探索
👀传送门👀 🔍引言🍀神经网络的基本原理🚀神经网络的结构📕神经网络的训练过程🚆神经网络的应用实例💖未来发展趋势💖结语 🔍引言 随着人工智能技术的飞速发…...
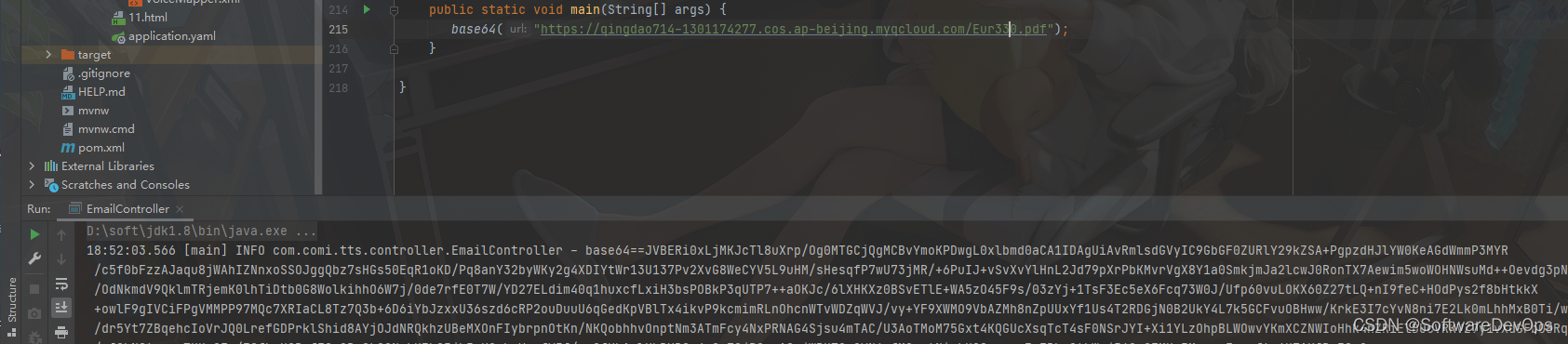
Java如何实现pdf转base64以及怎么反转？
问题需求 今天在做发送邮件功能的时候，发现邮件的附件部分，比如pdf文档，要求先把pdf转为base64，邮件才会发送。那接下来就先看看Java 如何把 pdf文档转为base64。 两种方式，一种是通过插件 jar 包的方式引入…...
动态规划5：62. 不同路径
动态规划解题步骤： 1.确定状态表示：dp[i]是什么 2.确定状态转移方程：dp[i]等于什么 3.初始化：确保状态转移方程不越界 4.确定填表顺序：根据状态转移方程即可确定填表顺序 5.确定返回值 题目链接：62. …...
Python编程学习第一篇——Python零基础快速入门（五）-列表（List）
今天我们来一起学习Python的列表（list），Python中的列表（List）是一种有序、可变的数据结构，可以用来存储多个值。列表可以包含不同类型的数据，例如整数、浮点数、字符串等。以下是关于Python列表…...
c# - 运算符 ＜＜ 不能应用于 long 和 long 类型的操作数
Compiler Error CS0019 c# - 运算符 << 不能应用于 long 和 long 类型的操作数 处理方法 特此记录 anlog 2024年5月30日...
)
问题排查｜记录一次基于mymuduo库开发的服务器错误排查(回响服务器无法正常工作)
问题背景： 服务器程序如下： #include <mymuduo/TcpServer.h> #include <mymuduo/Logger.h>#include <string> #include <functional>class EchoServer { public:EchoServer(EventLoop *loop,const InetAddress &addr, con…...
中介模式实现聊天室
中介者模式的核心逻辑就是解耦对象‘多对多’的相互依赖关系。当遇到一大堆混乱的对象呈现“网状结构”，利用通过中介者模式解耦对象之间的通讯。 代码案例 抽象中介类 public abstract class AbstractChatRoom {public abstract void notice(String message , Us…...
游戏开发与游戏设计区别
游戏设计与游戏开发是两个紧密相关但有着不同重点的领域，通常需要不同的技能和流程。以下是对游戏设计与游戏开发的详细解释，以及两者的区别： 游戏设计是关于构思和规划游戏的内容、机制和体验的过程。 主要内容: 故事和情节：构…...
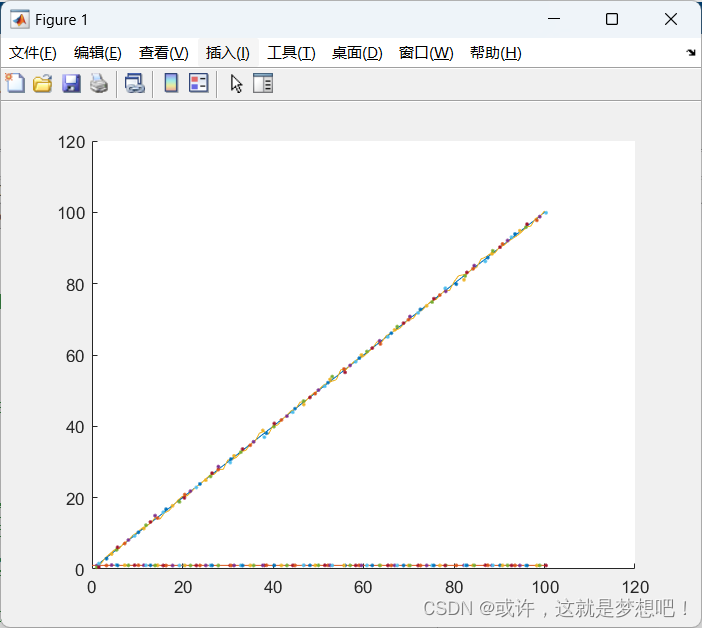
卡尔曼滤波算法的matlab实现
卡尔曼滤波算法的matlab实现 figure; hold on;Z(1:1:100); %观测值：第一秒观测1m 第二秒观测两米 匀速运动, 每秒1m, 最后拟合的也是速度 1m/splot(Z); plot([0,100], [1,1]);noiserandn(1,100)*0.5; %生成方差为1的高斯噪声 ZZnoise; % 加入噪声plot(Z);X[0;…...
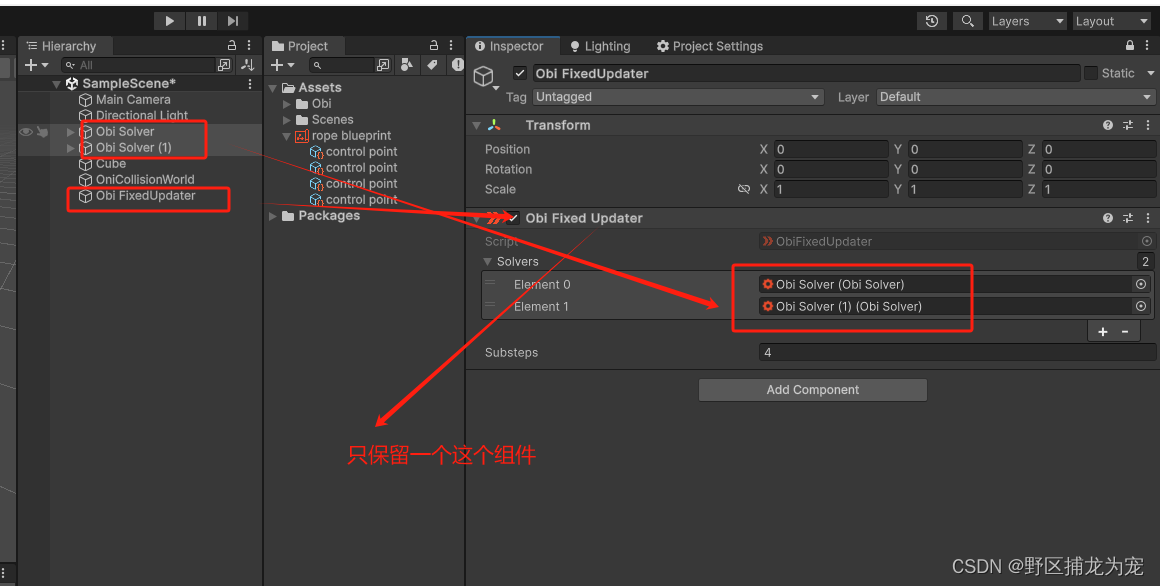
Unity Obi Rope失效
文章目录 前言一、WebGL端Obi Rope失效二、Obi Rope 固定不牢三、使用Obi后卡顿总结 前言 Obi 是一款基于粒子的高级物理引擎，可模拟各种可变形材料的行为。 使用 Obi Rope，你可以在几秒内创建绳索和杆子，同时完全控制它们的形状和行为&…...
基于Nginx和Consul构建自动发现的Docker服务架构——非常之详细
基于Nginx和Consul构建自动发现的Docker服务架构 文章目录 基于Nginx和Consul构建自动发现的Docker服务架构资源列表基础环境一、安装Docker1.1、Consul节点安装1.2、registrator节点安装 二、案例前知识点2.1、什么是Consul 三、基于Nginx和Consul构建自动发现的Docker服务架构…...
Gnu/Linux 系统编程 - 如何获取帮助及一个演示
Gnu/Linux 系统编程 - 如何获取帮助及一个演示 今天开始写 Gnu/Linux 环境下的系统编程，主要的用的语言是 C，主要是为了学习 C 语言，边学边写，这样的学习速度是比较快的。 今天就先介绍下如何在手头上没有任何资料的情况下&…...
iOS 26 携众系统重磅更新，但“苹果智能”仍与国行无缘
美国西海岸的夏天，再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至，这不仅是开发者的盛宴，更是全球数亿苹果用户翘首以盼的科技春晚。今年，苹果依旧为我们带来了全家桶式的系统更新，包括 iOS 26、iPadOS 26…...
Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件，常用于在两个集合之间进行数据转移，如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model：绑定右侧列表的值&…...
可靠性+灵活性：电力载波技术在楼宇自控中的核心价值
可靠性灵活性：电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中，电力载波技术（PLC）凭借其独特的优势，正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据，无需额外布…...
江苏艾立泰跨国资源接力：废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下，江苏艾立泰以一场跨国资源接力的创新实践，重新定义了绿色供应链的边界。 跨国回收网络：废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点，将海外废弃包装箱通过标准…...
python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式（Python 实现） 在 Python 中，你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是，.doc 是旧的 Word 格式，而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
如何理解 IP 数据报中的 TTL？
目录 前言理解 前言 面试灵魂一问：说说对 IP 数据报中 TTL 的理解？我们都知道，IP 数据报由首部和数据两部分组成，首部又分为两部分：固定部分和可变部分，共占 20 字节，而即将讨论的 TTL 就位于首…...
Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ；并安装。 基础操作不再赘述。 打开 macOS 终端，开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
腾讯云V3签名
想要接入腾讯云的Api，必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口，但总是卡在签名这一步，最后放弃选择SDK，这次终于自己代码实现。 可能腾讯云翻新了接口文档，现在阅读起来，清晰了很多&…...
C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称：装饰器模式（Decorator Pattern） 👦 小明最近上线了校园奶茶配送功能，业务火爆，大家都在加料： 有的同学要加波霸 🟤，有的要加椰果…...
「全栈技术解析」推客小程序系统开发：从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下，推客小程序系统凭借其裂变传播、精准营销等特性，成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径，助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...