Debian和ubuntu 嵌入式的系统的 区别

随着开源操作系统的日益流行,Debian和Ubuntu这两个基于Linux的发行版本成为了众多开发者和系统管理员的首选。它们各自拥有独特的优势和特点,那么,在选择时,哪一个更适合你呢?接下来,我们将深入探讨两者的关键区别,帮助你做出明智的决策。
一、起源与历史
Debian,诞生于1993年,是Linux世界中最古老和最重要的发行版之一。它以其强大的稳定性和严格的软件包管理政策而闻名。而Ubuntu,则是基于Debian的一个分支,诞生于2004年,以易用性和对桌面环境的优化著称。
二、软件包管理
Debian使用APT(Advanced Package Tool)作为其软件包管理工具,为用户提供了强大的包搜索、安装、升级和删除功能。而Ubuntu也沿用了这一工具,但进行了进一步的优化和简化,使得用户在使用时更为便捷。
三、稳定性与更新
Debian以其卓越的稳定性而著称,其发行周期相对较长,通常每隔两到三年才发布一个新的稳定版本。这使得Debian成为那些追求高度稳定性的服务器和大型系统的理想选择。而Ubuntu则采用了更为灵活的发布策略,每六个月发布一个新的长期支持版本(LTS),这使得Ubuntu在桌面和云环境等领域更具竞争力。
四、社区支持
作为开源社区中的佼佼者,Debian和Ubuntu都拥有庞大的用户群体和活跃的社区支持。Ubuntu的社区尤其以其友好和乐于助人的氛围而著称,这使得新手在遇到问题时能够得到及时的帮助。而Debian的社区则更加注重技术的深入讨论和开源精神的传承。
五、桌面与服务器环境
Ubuntu在桌面环境方面进行了大量的优化和改进,提供了更加美观和易用的界面。这使得Ubuntu成为了许多桌面用户的首选。而Debian则更加注重服务器环境的优化,其强大的稳定性和高效的资源利用使得它在服务器领域有着广泛的应用。
总结
Debian和Ubuntu都是优秀的Linux发行版,各自具有独特的优势和特点。在选择时,你可以根据自己的需求进行权衡。如果你追求高度的稳定性和长期的稳定性支持,Debian将是一个不错的选择。而如果你更注重易用性和活跃的社区支持,Ubuntu则可能是更好的选择。无论选择哪一个,你都将享受到开源世界的无尽魅力。
相关文章:

Debian和ubuntu 嵌入式的系统的 区别
随着开源操作系统的日益流行,Debian和Ubuntu这两个基于Linux的发行版本成为了众多开发者和系统管理员的首选。它们各自拥有独特的优势和特点,那么,在选择时,哪一个更适合你呢?接下来,我们将深入探讨两者的关…...

HTML旋转照片盒子
效果图 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv"X-UA-Compatible" content…...
【UE5 刺客信条动态地面复刻】实现无界地面01:动态生成
2024.6.4更新 昨天半夜意识到生成Cube的方案不合适,又开始到处找动态地面的方法,发现了我想要的效果直接可以用nigara实现!!!! 于是这个部分就暂时告一段落,今季开始新的方向的学习。 为了快速…...

AI产品经理系列-如何使用kimi快速撰写用户故事(含提示词)
在AI时代,可能人人都可成为产品经理。 之前我们聊过如何使用kimi协助完成产品需求文档,如何写竞品分析报告,这一篇我们聊聊用户故事,如何使用kimi协助撰写产品需求文档中的用户故事。 在此之前我们先了解下什么是用户故事&#…...
MySQL索引与事务
前言👀~ 紧接着数据库的相关知识,今天讲解MySQL面试中频繁被问到的知识点,索引与事务!!! 如果各位对文章的内容感兴趣的话,请点点小赞,关注一手不迷路,如果内容有什么问题的话,欢迎各位评论纠正…...

『大模型笔记』从基础原理出发提升深度学习性能
从基础原理出发提升深度学习性能 文章目录 一. 从基础原理出发提升深度学习性能1.1. 计算(compute)1.2. 带宽(Bandwidth)1.2.1 关于内存带宽成本的推理(Reasoning about Memory-Bandwidth Costs)1.3. 开销(Overhead)二. 总结三. 参考文献Making Deep Learning Go Brrrr F…...
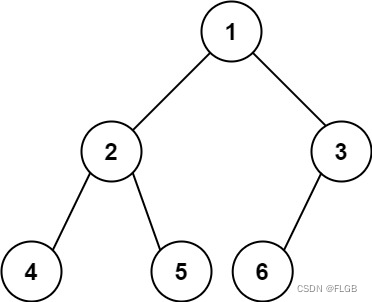
【二叉树】Leetcode 222. 完全二叉树的节点个数【简单】
完全二叉树的节点个数 你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最…...

golang界面设计器,全网少见
今天登录govcl的网站,无意中看到有个简易UI设计器。 对于golang的UI专用设计器,还没在网上真正见过。 之前也用govcl来做过两三个桌面应用,好用是好用,不过要安装Lazarus的IDE来拖动设计UI,还要配置很多东西࿰…...
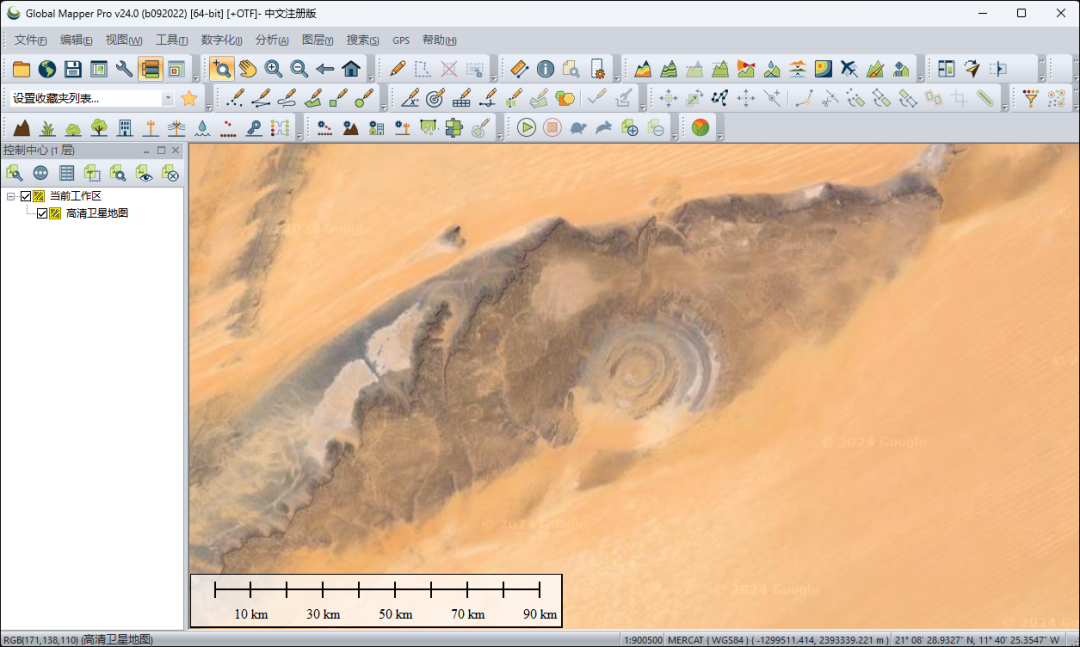
如何在GlobalMapper中加载高清卫星影像?
GlobalMapper在GIS行业几乎无人不知,无人不晓,但它可以直接加载卫星影像也许就不是每个人都知道的了。 这里就来分享一下如何在GlobalMapper中加载高清卫星影像,并可以在文末查看领取软件安装包和图源的方法。 如何加载高清图源 首先&…...

【机器学习】解锁AI密码:神经网络算法详解与前沿探索
👀传送门👀 🔍引言🍀神经网络的基本原理🚀神经网络的结构📕神经网络的训练过程🚆神经网络的应用实例💖未来发展趋势💖结语 🔍引言 随着人工智能技术的飞速发…...
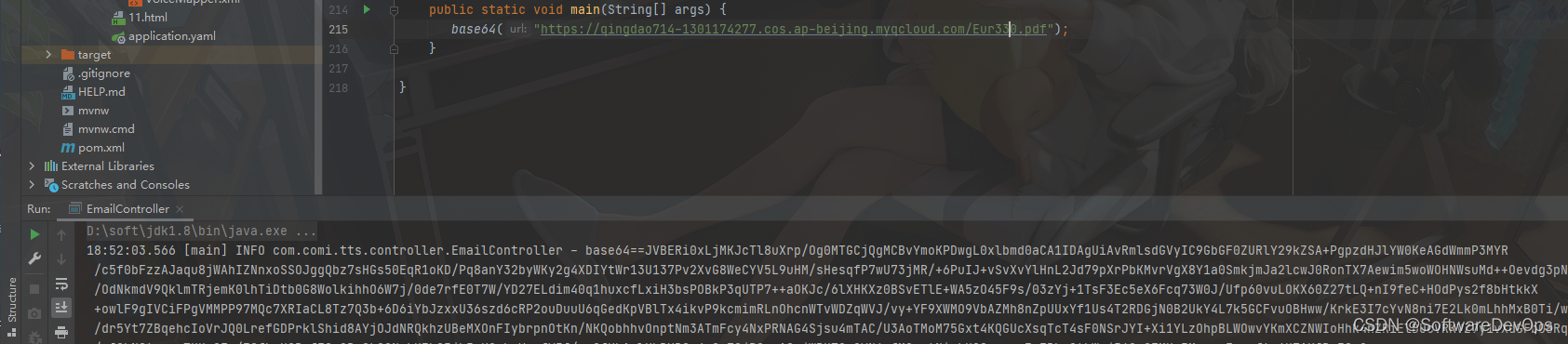
Java如何实现pdf转base64以及怎么反转?
问题需求 今天在做发送邮件功能的时候,发现邮件的附件部分,比如pdf文档,要求先把pdf转为base64,邮件才会发送。那接下来就先看看Java 如何把 pdf文档转为base64。 两种方式,一种是通过插件 jar 包的方式引入…...

动态规划5:62. 不同路径
动态规划解题步骤: 1.确定状态表示:dp[i]是什么 2.确定状态转移方程:dp[i]等于什么 3.初始化:确保状态转移方程不越界 4.确定填表顺序:根据状态转移方程即可确定填表顺序 5.确定返回值 题目链接:62. …...
-列表(List))
Python编程学习第一篇——Python零基础快速入门(五)-列表(List)
今天我们来一起学习Python的列表(list),Python中的列表(List)是一种有序、可变的数据结构,可以用来存储多个值。列表可以包含不同类型的数据,例如整数、浮点数、字符串等。以下是关于Python列表…...

c# - 运算符 << 不能应用于 long 和 long 类型的操作数
Compiler Error CS0019 c# - 运算符 << 不能应用于 long 和 long 类型的操作数 处理方法 特此记录 anlog 2024年5月30日...
)
问题排查|记录一次基于mymuduo库开发的服务器错误排查(回响服务器无法正常工作)
问题背景: 服务器程序如下: #include <mymuduo/TcpServer.h> #include <mymuduo/Logger.h>#include <string> #include <functional>class EchoServer { public:EchoServer(EventLoop *loop,const InetAddress &addr, con…...

中介模式实现聊天室
中介者模式的核心逻辑就是解耦对象‘多对多’的相互依赖关系。当遇到一大堆混乱的对象呈现“网状结构”,利用通过中介者模式解耦对象之间的通讯。 代码案例 抽象中介类 public abstract class AbstractChatRoom {public abstract void notice(String message , Us…...

游戏开发与游戏设计区别
游戏设计与游戏开发是两个紧密相关但有着不同重点的领域,通常需要不同的技能和流程。以下是对游戏设计与游戏开发的详细解释,以及两者的区别: 游戏设计是关于构思和规划游戏的内容、机制和体验的过程。 主要内容: 故事和情节:构…...
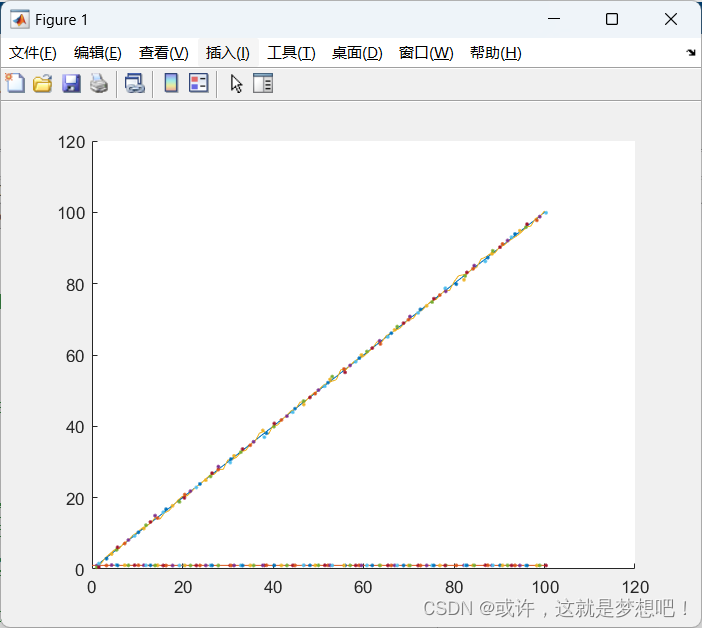
卡尔曼滤波算法的matlab实现
卡尔曼滤波算法的matlab实现 figure; hold on;Z(1:1:100); %观测值:第一秒观测1m 第二秒观测两米 匀速运动, 每秒1m, 最后拟合的也是速度 1m/splot(Z); plot([0,100], [1,1]);noiserandn(1,100)*0.5; %生成方差为1的高斯噪声 ZZnoise; % 加入噪声plot(Z);X[0;…...
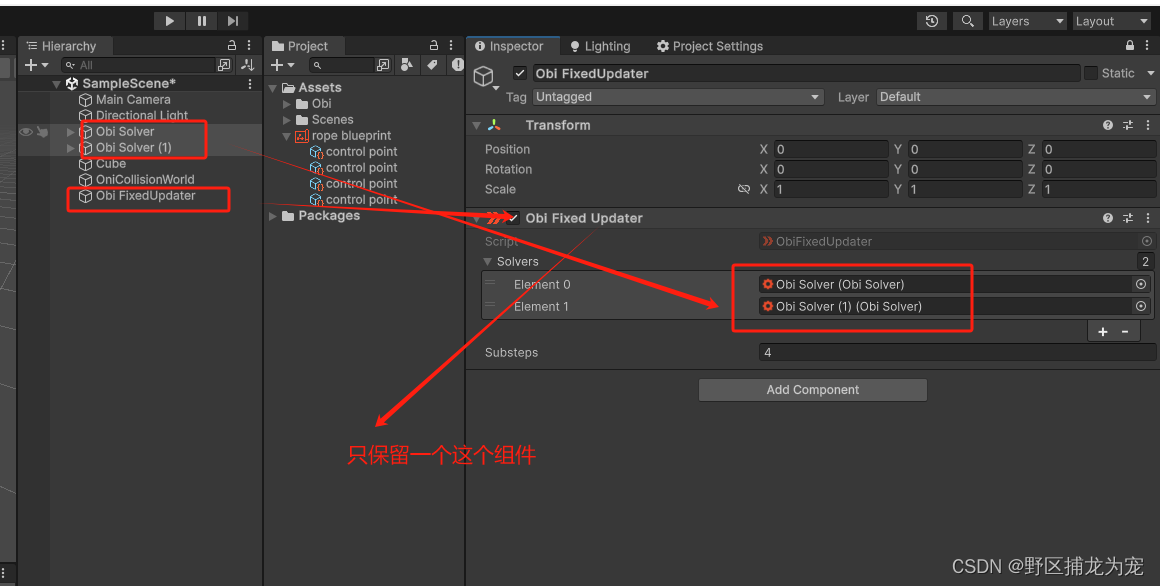
Unity Obi Rope失效
文章目录 前言一、WebGL端Obi Rope失效二、Obi Rope 固定不牢三、使用Obi后卡顿总结 前言 Obi 是一款基于粒子的高级物理引擎,可模拟各种可变形材料的行为。 使用 Obi Rope,你可以在几秒内创建绳索和杆子,同时完全控制它们的形状和行为&…...
基于Nginx和Consul构建自动发现的Docker服务架构——非常之详细
基于Nginx和Consul构建自动发现的Docker服务架构 文章目录 基于Nginx和Consul构建自动发现的Docker服务架构资源列表基础环境一、安装Docker1.1、Consul节点安装1.2、registrator节点安装 二、案例前知识点2.1、什么是Consul 三、基于Nginx和Consul构建自动发现的Docker服务架构…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
