数据分析------统计学知识点(三)
相关性分析
1.趋势分析与散点图
散点图可帮助我们发现和理解变量间的关系,可直观观察是否有相关性。
(1)散点图定义及组成要素
散点图是一种以点的形式在直角坐标系上表示两个数值变量间关系的图表
横坐标(x轴):代表独立变量,如广告预算
纵坐标(y轴):代表因变量,如销售额
数据点:表示记录的坐标点,反映变量间的关系
(2)散点图表意原则
正相关:点呈现从左下到右上的趋势,意味着一个变量的增加通常伴随着另一变量的增加。
负相关:点分布从左上到右下,一个变量的增加伴随着另一个变量的减少
非线性相关:点分布呈曲线形状,表明变量间的关系更复杂
(3)散点图洞察数据的技巧
为最大化散点图的价值,以下技巧是必需的
(a)使用趋势线:加入趋势线可帮助我们1更清晰地看到数据的整体方向和强度
(b)调整透明度:当数据点过多重叠时,调整点的透明度可以更好的显示分布情况
(c)考虑数据密度:使用颜色深浅或大小代表数据密集区域,可以更好的揭示聚类效应
(4)散点图分析注意事项
异常值:可能会影响趋势的判断,需仔细分析其背后的原因
聚类:数据聚类在某些区域可能会隐藏其他区域的特征
非因果相关:相关性并不代表因果关系,需要防止错误解读
(5)幸存者偏差及其影响
幸存者偏差指的是在分析过程中,只关注“幸存”的数据,而忽略了那些因各种原因而未被观察到的数据。在散点图分析中,这可能导致对关系的错误评估。
2.相关性分析概念
相关性分析是衡量两个变量间的关系强度和方向的统计手段,它帮助我们理解不同数据之间的相互作用。
3.常用计算方法
皮尔逊相关系数:衡量两个变量线性相关程度的指标,取值范围在-1到1之间,其中1表示完全正相关,-1表示完全负相关,0表示无线性相关。
斯皮尔曼等级相关系数:是一种非参数的相关性衡量方法,用来评价两个变量的等级或顺序间的相关性。
4.方法优缺点、适用条件和计算步骤
皮尔逊相关系数
优点:适用评估线性关系强度
缺点:对异常值敏感,只能用于连续变量
适用条件:两变量均为连续且大致呈正态分布
计算步骤:标准化变量,计算协方差,除以两变量的标准差的乘积
斯皮尔曼等级相关系数
优点:不要求数据正态分布,对异常值不敏感
缺点:只能捕捉单调关系
适用条件:至少有一个变量是有序分类变量
计算步骤:对每个变量进行等级排序,计算等级之间的皮尔逊相关系数
5.相关性分析的经典应用场景
①金融领域:分析股票价格与市场因素的相关性
②医学研究:探究生活习惯与健康状况的相关性
③社会科学:研究教育水平与收入水平的关系
④市场营销:评估广告投放与品牌知名度的相关性
6.鉴别相关性陷阱的建议
①多角度分析:结合其他图表和统计方法,全面了解数据
②数据清洗:识别并处理异常值和缺失数据
③专业知识:结合领域知识,合理解释数据关系
7.互联网场景下的相关性分析
相关性分析帮助企业从大数据中提取有价值的信息,实现精准营销和服务
电商:分析用户属性与购买行为的相关性
通过用户年龄、地域、历史购买数据等属性与其购买时间之间的相关性分析,可以实现个性化推荐,提高转化率
社交媒体:研究用户互动行为背后的相关因素
分析点赞、评论等用户互动行为与内容特征、发布时间等因素的关系,有助于优化内容推送策略
搜索引擎:挖掘搜索query与用户属性的相关性
关联用户的查询关键词与其个人信息,可以优化搜索算法,提高更为精准的搜索结果
在线广告:利用相关性分析给用户投放最感兴趣的广告创意
结合用户的浏览历史、点击行为与广告点击率进行相关性分析,可以帮助精准投放广告,增加广告效果。
标准差
1.标准差:数据离散程度的度量
反映了数据与其平均值之间的偏离程度。标准差越大,说明数据的离散程度越高;反之标准差越小,数据的离散程度越低。除标准差,还可以用离散系数来描述数据的离散程度。
离散系数是标准差与平均值的比值,通常用百分数表示,可以让我们更直观的比较不同的数据集的离散程度,尤其是当它们的量纲or平均值差异较大时
2.标准差的应用
①识别异常值:若某个数据点与平均值的偏差超过2-3个标准差,则通常可将其识别为异常值,离群值。
②构建置信区间:在一定置信水平(常用95%),我们可以用标准差构建一个区间,该区间有很大概率包含总体的真实参数。
③比较不同组别的数据:通过比较不同的组别数据的标准差,我们可以了解哪个组的数据更稳定,哪个组的数据波动更大。
3.标准误差:抽样误差的度量
实际工作通常无法获取全部总体数据,而只能通过抽样的方式来推断总体特征。标准误差就是用来描述由于抽样引入的误差。
公式:标准误差=标准差/根号n,n为样本量。样本量越大,标准误差越小,即抽样误差越小。
4.标准误差的应用
①估计总体参数
利用样本统计量和标准误差,可构建总体参数的置信区间,从而对总体参数进行估计。
②比较不同样本的差异
当想要比较两个或多个样本的均值时,可利用标准误差计算它们之间的差异是否具有统计学意义。
③确定样本量
在设计抽样调查时,可根据标准误差的大小来确定所需的样本量,以控制抽样误差在可接受的范围内。
5、互联网企业的应用场景
①用户行为分析:分析用户的活跃度、留存率、付费金额等指标时,可利用标准差来识别不同用户群体之间的差异,找出高价值用户or流失风险用户
②A/B测试:进行产品优化时,通常会将用户随机分成两组或多组,分别体验不同的产品版本,通过比较不同组别的关键指标(eg:转化率、点击率)的均值、标准误差,可判断哪个版本表现优
③广告效果评估:对于广告投放,我们需要评估不同广告创意或投放渠道的效果,利用标准差和标准误差,我们可以比较不同的广告或渠道的点击率、转化率等指标优化广告策略。
④异常检测:在实时监控系统的关键指标时,可利用标准差来设置异常阈值。当指标偏离平均值超过一定的标准差时,系统就会自动报警,提醒数据分析师及时处理潜在的问题。
相关文章:
)
数据分析------统计学知识点(三)
相关性分析 1.趋势分析与散点图 散点图可帮助我们发现和理解变量间的关系,可直观观察是否有相关性。 (1)散点图定义及组成要素 散点图是一种以点的形式在直角坐标系上表示两个数值变量间关系的图表 横坐标(x轴)&a…...

MySQL 导出一条数据的插入语句
1.MySQL 导出一条数据的插入语句的方法 在MySQL中,如果我们想要导出一条数据的插入语句,我们可以使用SELECT ... INTO OUTFILE语句(但这通常用于将整个表或查询结果导出到一个文件中),或者我们可以手动构建插入语句。…...

隐藏 IP 地址的重要性是什么?
在当今的数字时代,保护我们的在线身份至关重要。从保护个人信息到保护隐私,互联网用户越来越多地寻求增强在线安全性的方法。保持匿名和保护敏感数据的一个关键方面是隐藏您的 IP 地址。在这篇博文中,我们将深入探讨隐藏 IP 地址的重要性&…...

Oracle 19c linux安装
下载Oracle Database Preinstallation RPM,该包会自动下载依赖,创建oracle用户, 手动下载地址:https://yum.oracle.com/repo/OracleLinux/OL7/latest/x86_64/index.html wget http://yum.oracle.com/repo/OracleLinux/OL7/latest…...
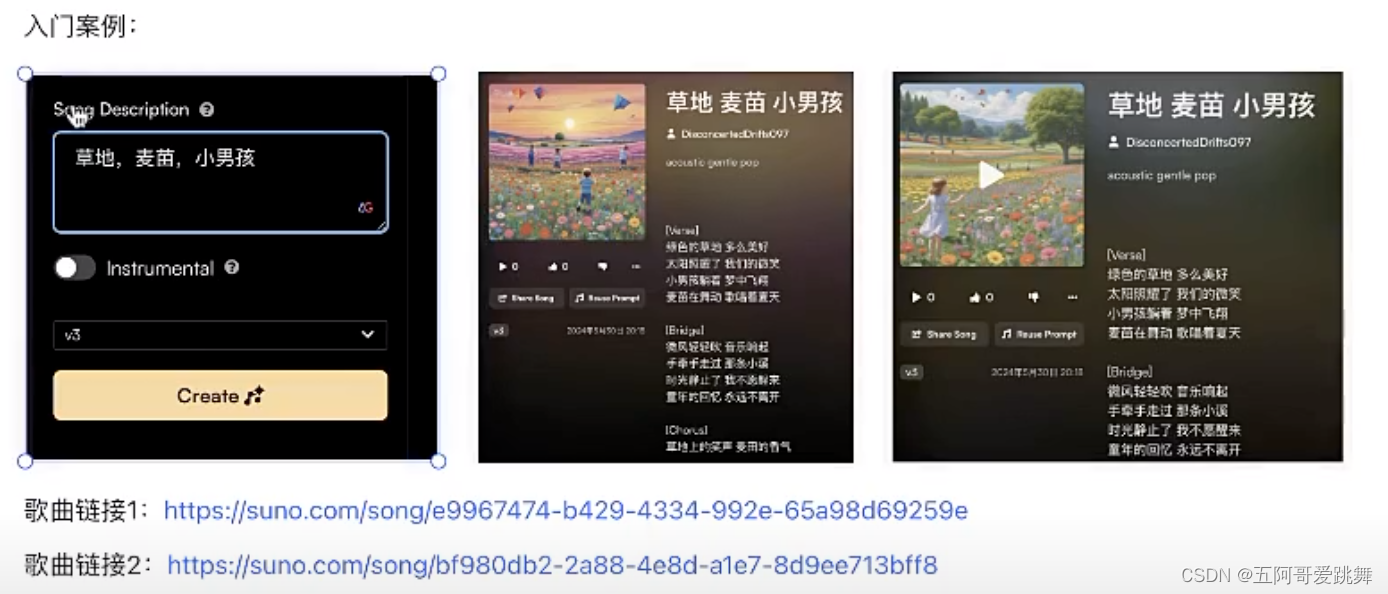
AI音乐生成流程
suno.com...

android room数据库升级脚本常见问题
room数据库升级很容易遇到一个问题, java.lang.IllegalStateException: Migration didnt properly handle: Expected:xxx Found:xxx 意思是数据库执行完你编写的升级脚本后,发现数据库当前的表结构与你代码中的Entity class结构不一致,所…...
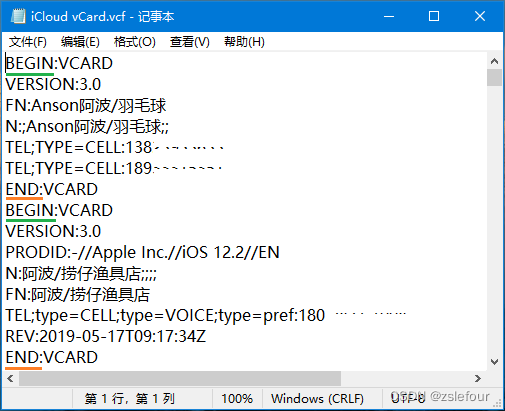
在 iCloud.com 上导入、导出或打印联系人
想将iPhone上的电话本备份一份到本地电脑上,发现iTunes好像只是音乐播放了,不再支持像电话本等功能,也不想通过其他第三方软件,好在可以通过iCloud进行导入导出。下面只是对操作过程进行一个图片记录而已,文字说明可以…...

JavaScript中this方法;var,let,constd区别;JSON是什么
this方法 1、在对象方法中, this 指向调用它所在方法的对象。 2、单独使用 this,它指向全局(Global)对象。 3、函数使用中,this 指向函数的所属者。 4、严格模式下函数是没有绑定到 this 上,这时候 this 是 undefined。 5、在 HT…...
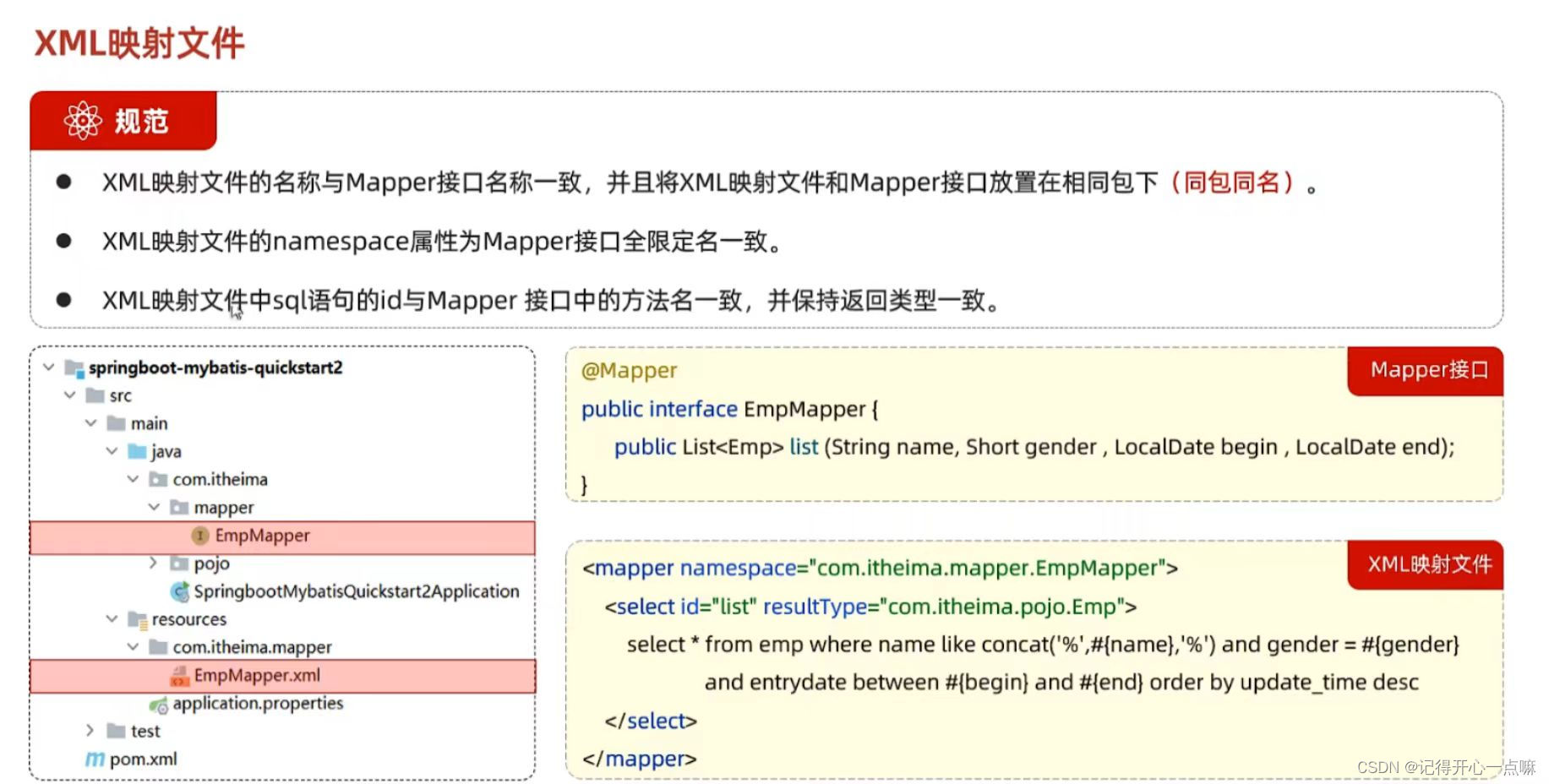
Mybatis不明白?就这一篇带你轻松入门
引言:烧脑的我一直在烧脑的寻找资料,寻找网课,历经磨难让一个在大一期间只会算法的我逐渐走入Java前后端开发,也是一直在自学的道路上磕磕碰碰,也希望这篇文章对于也是同处于自学的你有所帮助,也希望你继续…...

pymupdf提取pdf表格及表格数据合并
pymupdf提取pdf表格非常快速,相比其他库是个更好的选择. 一个行列多的表格打印成pdf后会由于页宽分页原因变成多个表格,提取的多个表格需要合并为一个表格,再来处理数据. 下面代码中merge函数用于合并表格࿰…...

门外汉一次过软考中级(系统集成项目管理工程师)秘笈,请收藏!
24上软考考试已经结束,24下软考备考又要开启了!今年软考发生了改革,很多考试由一年考两次变成了一年考一次,比如高级信息系统项目管理师,比如中级系统集成项目管理工程师,这两科是高、中级里相对简单&#…...
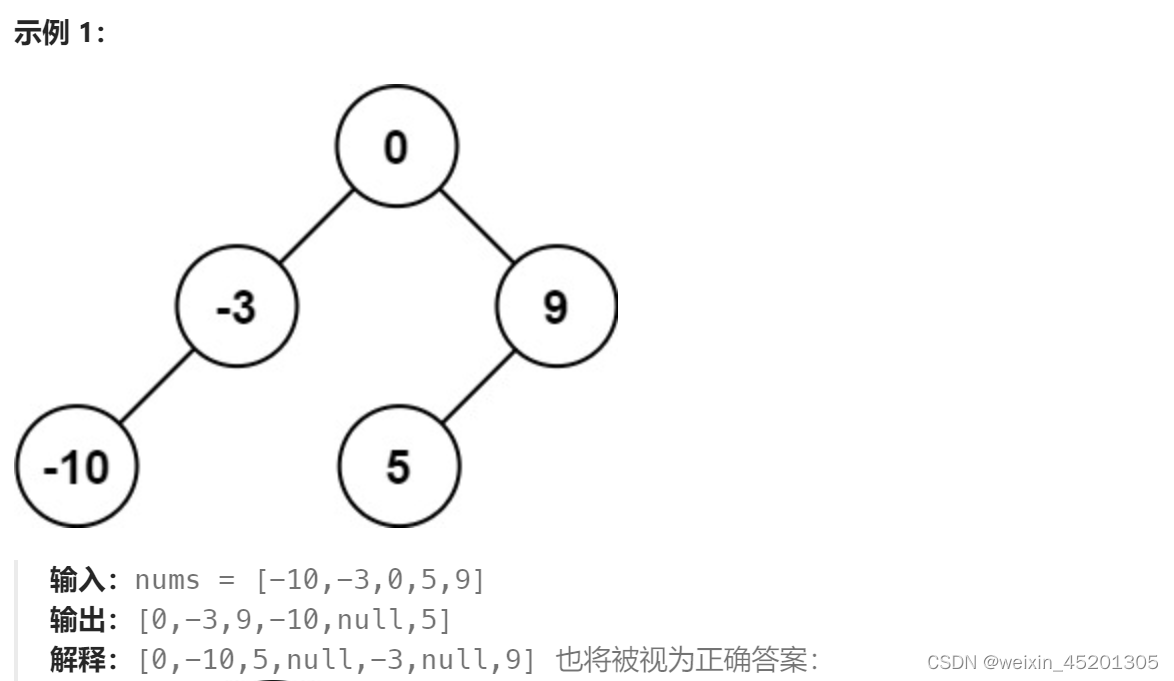
[leetcode hot 150]第一百零八题,将有序数组转换为二叉搜索树
题目:给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡二叉搜索树。 给定一个有序的整数数组,我们需要构建一棵平衡的二叉搜索树。平衡二叉树是指任意一个节点的左右子树的高度差不超过1。 由于给定的数组是有序的…...

科普丨什么是数字孪生灌区(平台)?如何建设?有何好处?
在农业发展的新时代,数字孪生灌区的概念逐渐走进大众视野,成为推动农业现代化、提升粮食安全保障能力的关键力量。那么,究竟什么是数字孪生灌区?它又是如何建设的?又能为我们带来哪些好处呢? 数字孪生灌区…...

Python爬虫如何入门:一步步走向精通的指南
Python爬虫如何入门:一步步走向精通的指南 在信息爆炸的时代,爬虫技术已经成为获取、整理和分析数据的必备技能。Python,以其简洁易懂的语法和强大的库支持,成为了爬虫开发的热门语言。那么,如何入门Python爬虫呢&…...

Linux用户和用户组的操作
用户管理 以Tom做为用户名 以dev做为用户组 增加用户 sudo adduser Tom #不建议使用useradd/userdel系列的命令删除用户 sudo deluser Tom --remove-home # 删除Tom用户及home目录 重置密码 sudo passwd Tom加入用户组 sudo usermod -a -G dev Tom # sudo usermod -aG …...
)
git命令行分支(增删改查)
文章目录 一、创建分支并推送到远程仓库二、拉取指定分支代码三、删除分支 一、创建分支并推送到远程仓库 初始化git git init如果有远程仓库就进行克隆远程仓库 origin 表示远程仓库地址 git clone origin# 如果没有远程仓库 就进行创建一个远程仓库 git remote add origin ht…...

地理加权回归GWR简介
地理加权回归GWR简介 一、定义: 地理加权回归(Geographically Weighted Regression,简称GWR)是一种空间数据分析方法,专门用于处理空间异质性(spatial heterogeneity)问题。以下是对GWR的详细简…...
康谋技术 | 自动驾驶:揭秘高精度时间同步技术(一)
众所周知,在自动驾驶中,主要涵盖感知、规划、控制三个关键的技术层面。在感知层面,单一传感器采集外界信息,各有优劣,比如摄像头采集信息分辨率高,但是受外界条件影响较大,一般缺少深度信息&…...
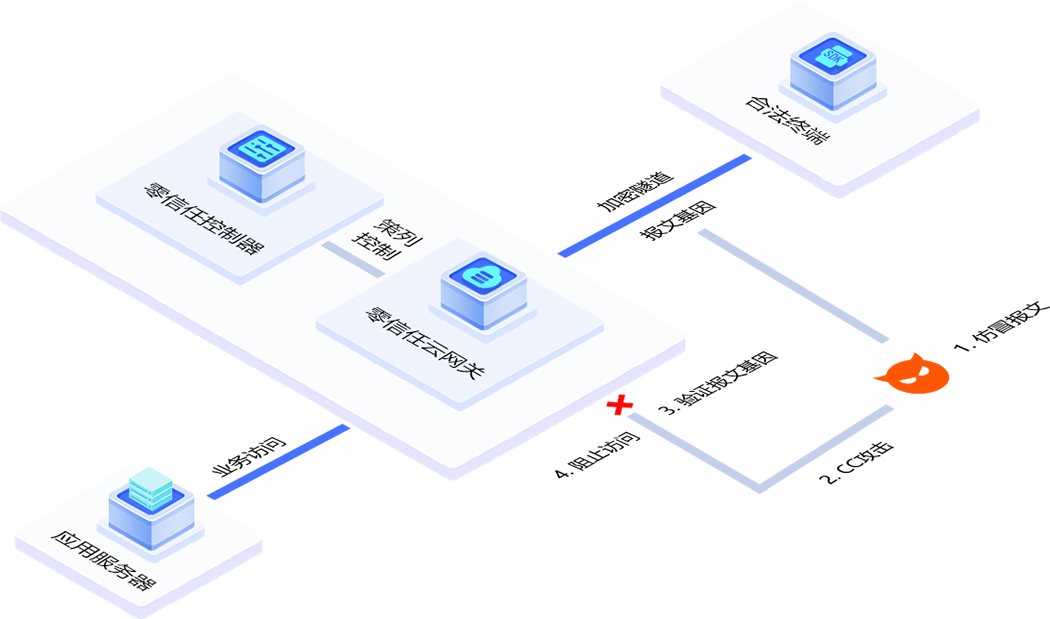
客户端被攻击怎么办,为什么应用加速这么适合
随着科技的进步和互联网的普及,游戏行业也正在经历前所未有的变革。玩家们不再满足于传统的线下游戏,而是转向了线上游戏。然而,随着游戏的线上化,游戏安全问题也日益凸显。游戏受到攻击是游戏开发者永远的痛点,谈“D“…...

Introduction to HAL3
目录 HAL3 behavior Overview of HAL1 v.s HAL3 HAL3 behavior: HAL3 - detail: HAL3 operation and pipeline Framework Diagram Problem of current code Operation mode Full v.s limited Do: Don’t: Metadata Manual control – ISP control...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
