【介绍下WebStorm开发插件】

🎥博主:程序员不想YY啊
💫CSDN优质创作者,CSDN实力新星,CSDN博客专家
🤗点赞🎈收藏⭐再看💫养成习惯
✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进步!
📝目录
- 📝前言
- 📝基础步骤
- 📝学习资源
- 📝重要提示
📝前言
🔝开发WebStorm插件可以让你为这个流行的JavaScript IDE添加自定义功能,如果你对开发WebStorm插件感兴趣,以下是一些基本的步骤和资源来帮助你开始:
📝基础步骤
-
🔝了解WebStorm平台:
🌈WebStorm是基于IntelliJ平台构建的,因此你需要了解它的插件架构和API,可以从JetBrains Plugin SDK文档开始学习。 -
🔝配置开发环境:
- 🌈安装IntelliJ IDEA Community Edition(免费)或者Ultimate版(付费)。
- 🌈配置IDEA以用于开发其他JetBrains IDE的插件。
-
🔝创建新插件项目:
🌈在IDEA中,你可以选择"Create New Project",然后选择"IntelliJ Platform Plugin"。 -
🔝了解Plugin.xml:
🌈每个插件都需要一个plugin.xml文件,这个文件定义插件的元数据和配置信息,包括插件名称、版本、入口点以及对IDE其他组件的依赖关系等。 -
🔝编写插件代码:
🌈编写插件的主体代码,其中可能包含对IDE的API调用,实现自定义功能。 -
🔝测试插件:
🌈IntelliJ IDEA允许你在沙盒IDE实例中直接运行插件,这使得测试和调试变得更为容易。 -
🔝打包插件:
🌈将你的插件打包成一个zip文件,这个文件可以被安装到WebStorm中。 -
🔝发布插件:
🌈你可以在JetBrains Plugin Repository中提交你的插件,这样其他人就可以下载并使用它了。
📝学习资源
-
🔝JetBrains Plugin SDK文档:
🌈这是官方文档,包含了插件开发的各个方面,从基础到高级话题。 -
🔝Sample Plugin Projects:
🌈JetBrains官方提供了多个样例项目,通过学习和尝试这些项目能帮助你更好地理解如何开发插件。 -
🔝Community Forums and Support:
🌈访问JetBrains的社区论坛,并加入插件开发相关的谈话和讨论。 -
🔝WebStorm Blog:
🌈时不时发布关于新功能、技巧和教程的官方博客。
📝重要提示
- 🔝在开发插件时,需要确保你的插件和最新版本的WebStorm兼容,也需要定期更新以适应新版本的WebStorm。
- 🔝Jetbrains的插件市场有严格的质量控制,确保遵循最佳实践,并在发布前彻底测试你的插件。
🌈开发插件是一个不断学习和实践的过程,不要害怕尝试和犯错;JetBrains以及相关的社区通常情况下很乐意帮助解决开发过程中的问题。
相关文章:

【介绍下WebStorm开发插件】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
推荐丨一键申请SSL证书,让网站实现HTTPS访问!
申请HTTPS证书可以简化为以下几个直接步骤,以便您能快速理解和操作: 1. 确定证书类型: - 单域名证书:适用于一个特定域名。 - 通配符证书:适用于同一主域名下的所有子域名。 - 多域名证书:覆盖多个不同的域…...

交叉导轨在医疗设备上的作用!
随着医疗器械行业的需求逐步增长,交叉导轨给医疗器械行业带来了广阔的发展前景。作为重要的精密传动元件,交叉导轨具有寿命长、高精度、高刚性、高耐腐蚀性和高稳定性等优点,满足精密仪器上对产品的高要求使用场景。 在医疗设备领域中交叉导轨…...

【云原生】Docker Compose 使用详解
目录 一、前言 二、Docker Compose 介绍 2.1 Docker Compose概述 2.2 Docker Compose特点 2.3 Docker Compose使用场景 三、Docker Compose 搭建 3.1 安装docker环境 3.2 Docker Compose安装方式一 3.2.1 下载最新版/如果不是最新可替换最新版本 3.2.2 设置权限 3.2.…...
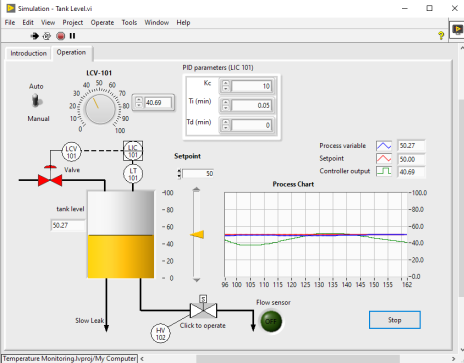
通过LabVIEW提升生产设备自动化水平
现代制造业对生产设备的自动化水平提出了越来越高的要求。使用LabVIEW这一强大的图形化编程环境,可以显著提升生产设备的自动化程度,改善生产效率和产品质量。本文将详细分析如何通过LabVIEW改善生产设备的自动化水平,并提供具体的实施策略与…...
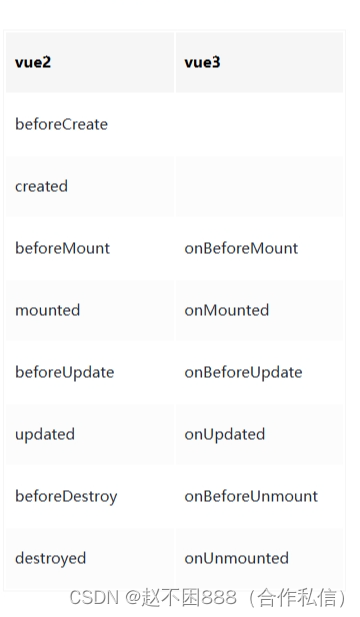
面试题vue+uniapp(个人理解-面试口头答述)未编辑完整....
1.vue2和vue3的区别(vue3与vue2的区别(你不知道细节全在这)_vue2和vue3区别-CSDN博客)参考 Vue3 在组合式(Composition )API,中使用生命周期钩子时需要先引入,而 Vue2 在选项API&am…...
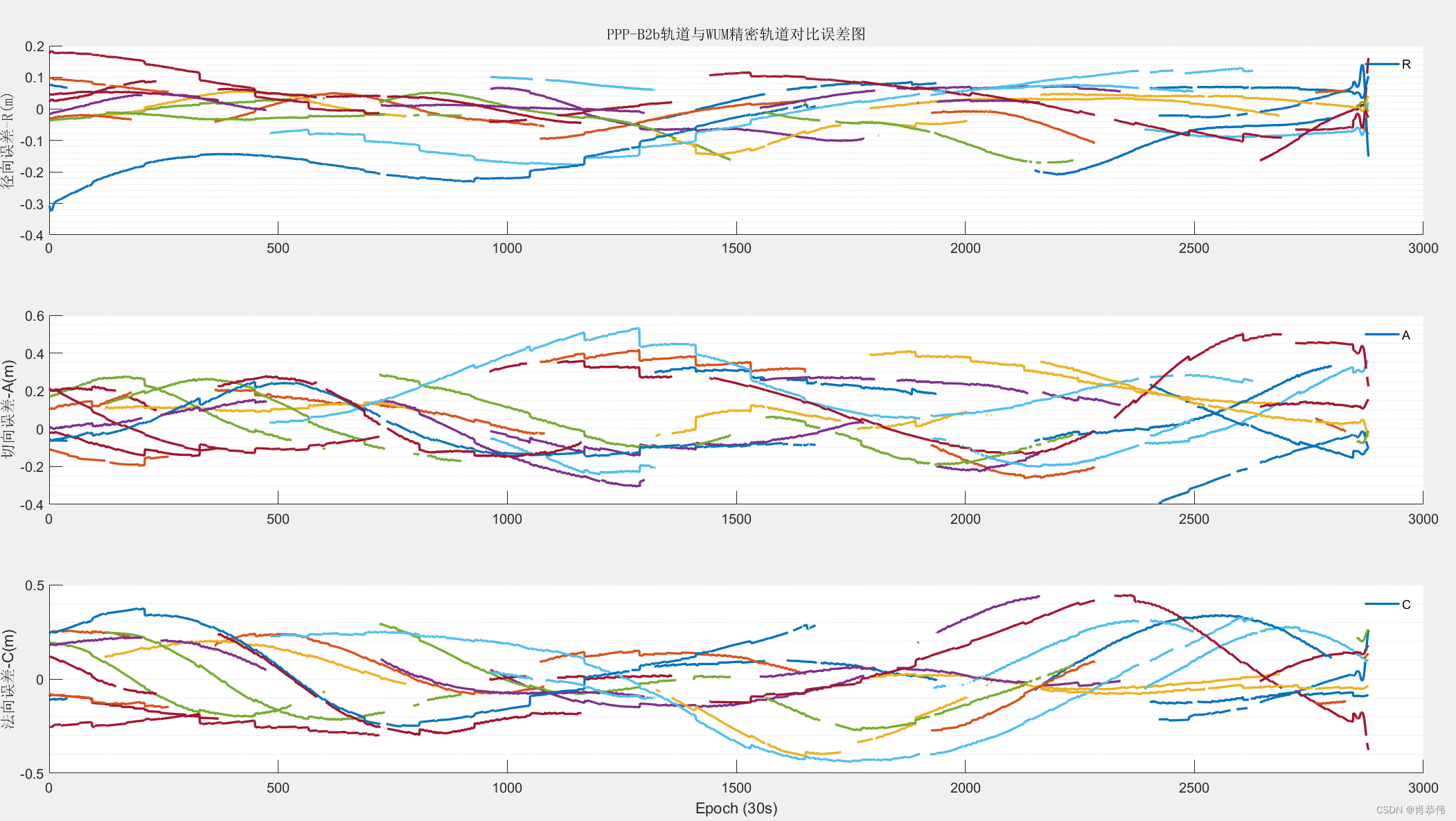
PPP-B2b精密产品使用注意事项及分析
1、因为在使用PPP-B2b进行定轨的时候,发的精密轨道产品是B3频点的,需要改正的卫星质心(Com)与SP3精密星历对比。 2、PPP-B2b产品吸收了电离层误差,因此电离层提取方面与IGS电离层完全无法对其。 3、由于PPP-B2b产品精…...
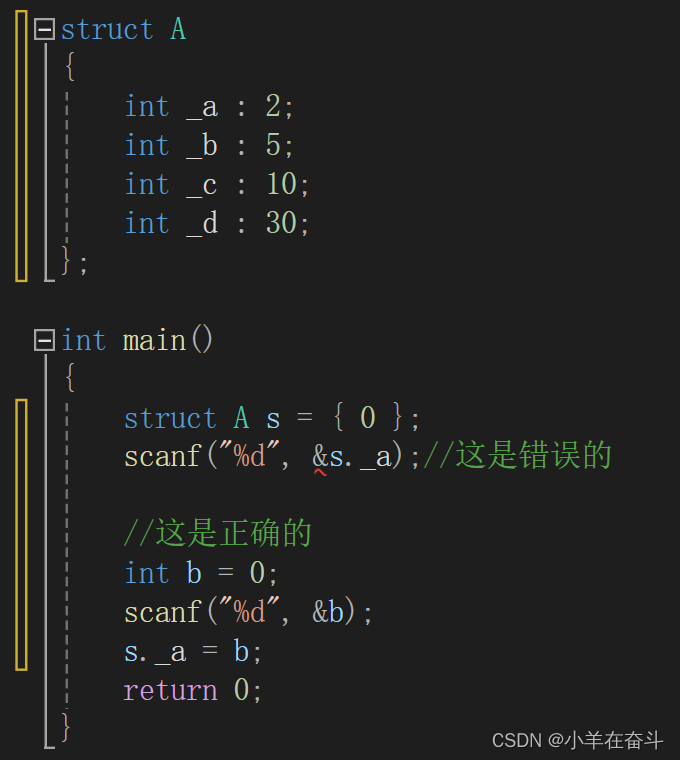
C语言(结构体)
Hi~!这里是奋斗的小羊,很荣幸各位能阅读我的文章,诚请评论指点,欢迎欢迎~~ 💥个人主页:小羊在奋斗 💥所属专栏:C语言 本系列文章为个人学习笔记,在这里撰写成文一…...
用法:深入解析与实战应用)
Python filter()用法:深入解析与实战应用
Python filter()用法:深入解析与实战应用 在Python编程中,filter() 函数是一个内置的高阶函数,它用于过滤序列,过滤掉不符合条件的元素,返回由符合条件元素组成的新列表。该函数在数据处理和筛选时非常有用࿰…...
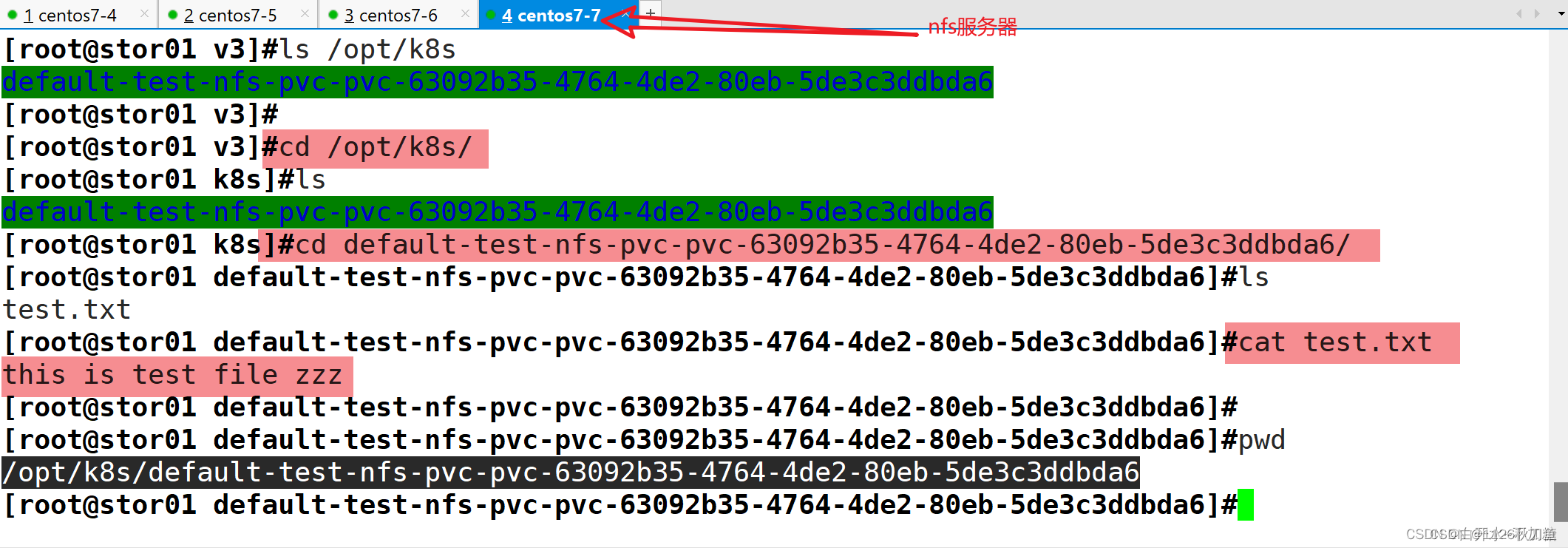
k8s集群的存储卷、pvc和pv
目录 简介 简介 PV 全称叫做 Persistent Volume,持久化存储卷。它是用来描述或者说用来定义一个存储卷的,这个通常都是由运维工程师来定义。 PVC 的全称是 Persistent Volume Claim,是持久化存储的请求。它是用来描述希望使用什么样的或者说…...

二分搜索树深度优先遍历
二分搜索树深度优先遍历 二分搜索树(Binary Search Tree,简称BST)是一种特殊的二叉树,它具有以下特性:对于树中的任意节点,其左子树中的所有元素都小于该节点的值,其右子树中的所有元素都大于该…...

ImportError: cannot import name ‘packaging‘ from ‘pkg_resources‘‘
参考自: [Bug]: ImportError: cannot import name packaging from pkg_resources (/usr/local/lib/python3.10/dist-packages/pkg_resources/__init__.py) Issue #15863 AUTOMATIC1111/stable-diffusion-webui GitHub ImportError: cannot import name packaging from pkg…...

灯塔歌曲音乐下载官网
灯塔歌曲音乐下载官网网址:www.dengtamp3.com 灯塔音乐下载上线以“用心服务,认真负责”为核心价值。 我们的团队是一个青春的团队,朝气蓬勃。我们采用最新的服务模式,以网为媒为广大客户提供服务,我们坚持以“用心&a…...

数据结构的归并排序(c语言版)
一.归并排序的基本概念 1.基本概念 归并排序是一种高效的排序算法,它采用了分治的思想。它的基本过程如下: 将待排序的数组分割成两个子数组,直到子数组只有一个元素为止。然后将这些子数组两两归并,得到有序的子数组。不断重复第二步,直到最终得到有序的整个数组。 2.核心…...

ubuntu使用Docker笔记
一、参考资料 1、B站视频 尚硅谷Docker实战教程 2、有心人整理的笔记 Docker笔记(周阳版) 3、菜鸟教程 Docker 教程 以下是本人的折腾实践。 二、Docker的安装 2.1、使用清华源安装docker,清华源官方教程。 本人是在ubuntu20.04下安装的…...

PHP编程入门:揭开Web开发的神秘面纱
PHP编程入门:揭开Web开发的神秘面纱 在数字化时代,PHP作为一种广泛使用的服务器端脚本语言,为Web开发领域注入了强大的活力。无论你是编程新手还是有一定经验的开发者,掌握PHP编程都将为你开启一扇通往Web开发新世界的大门。接下…...
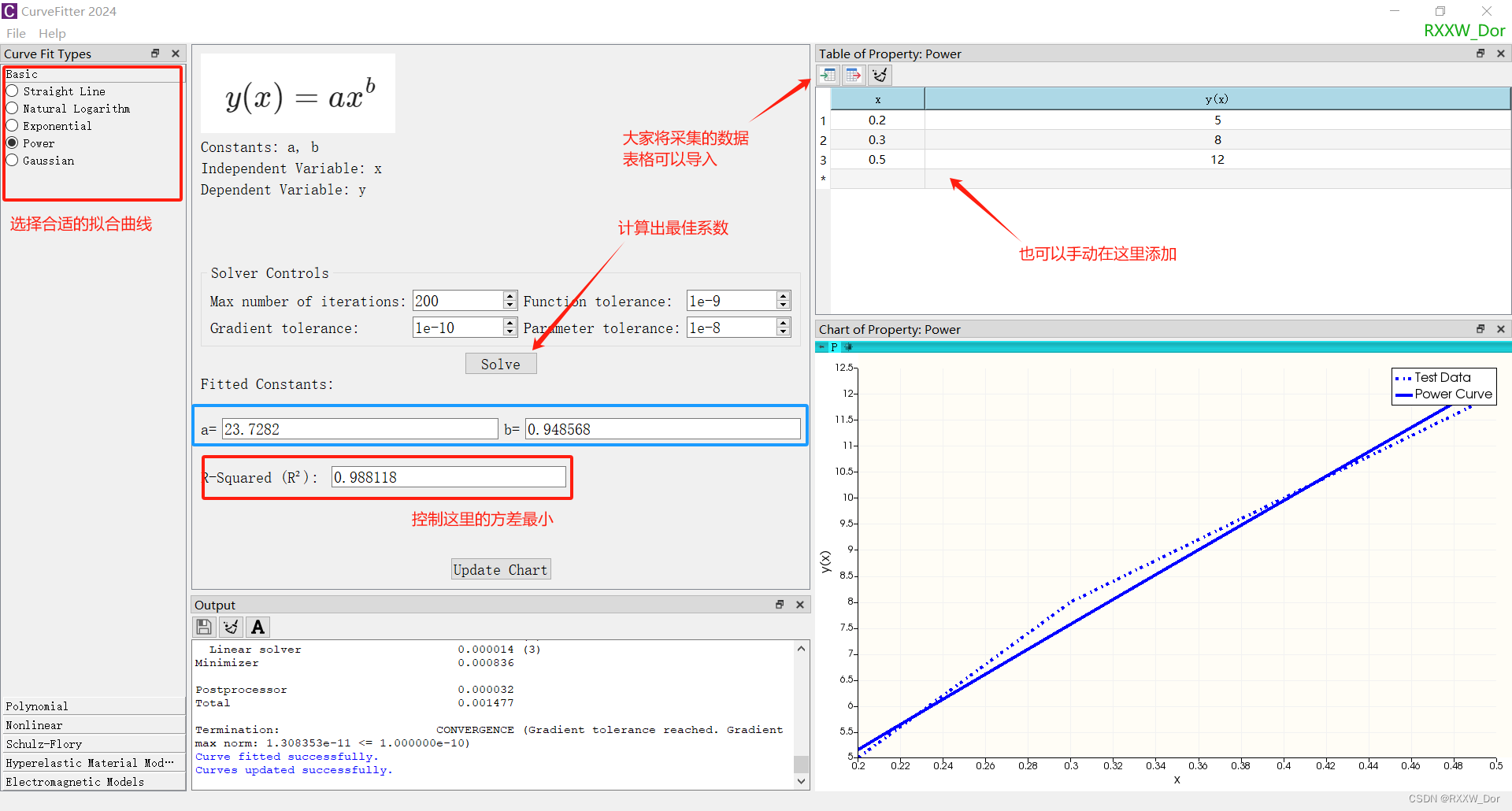
曲线拟合工具软件(免费)
曲线拟合是数据处理中经常用到的数值方法,本质是使用某一个模型(方程或者方程组)将一系列离散的数据拟合成平滑的曲线或者曲面,数值求解出对应的函数参数,大家可以利用MATLAB的曲线拟合工具箱也可以使用第三方的拟合软件,今天我们介绍Welsim免费的曲线拟合软件 1、MATLA…...
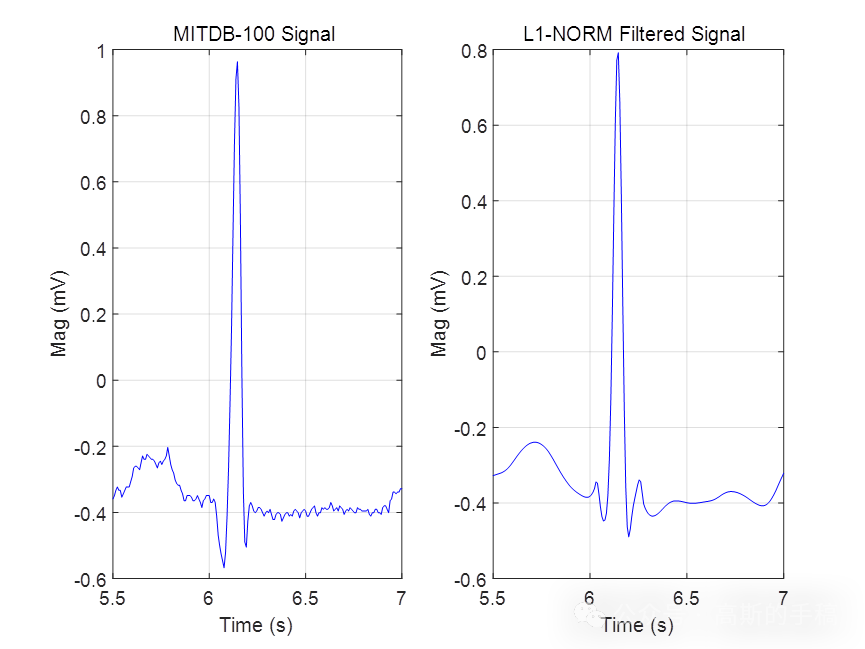
基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法(Matlab R2021B)
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量,它的非零系数相对较少,而Tikhonov正则化方法的解通常具有所有的非零系数。即:L2范数正则化方法的解通常是非稀疏的,并且解的结果在一…...
)
Bitbucket的原理及应用详解(一)
本系列文章简介: 在数字化和全球化的今天,软件开发和项目管理已经成为企业成功的关键因素之一。随着团队规模的扩大和项目的复杂化,如何高效地协同开发、管理代码和确保代码质量成为了开发者和管理者面临的重要挑战。Bitbucket作为一款功能强…...

企业级win10电脑下同时存在Python3.11.7Python3.6.6,其中Python3.6.6是后装的【过程与踩坑复盘】
背景: 需要迁移原始服务器的上的Python3.6.6+Flask项目到一个新服务器上, 新服务器上本身存在一个Python3.11.7, 所以这涉及到了一个电脑需要装多个Python版本的问题 过程: 1-确定新电脑版本【比如是32还是64位】 前面开发人员存留了两个包,是python-3.6.6.exe和pytho…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...
