交叉导轨在医疗设备上的作用!
随着医疗器械行业的需求逐步增长,交叉导轨给医疗器械行业带来了广阔的发展前景。作为重要的精密传动元件,交叉导轨具有寿命长、高精度、高刚性、高耐腐蚀性和高稳定性等优点,满足精密仪器上对产品的高要求使用场景。
在医疗设备领域中交叉导轨可以提供高精度、高稳定性的运动支撑,在医疗器械行业起着关键性作用。
1、在核磁共振设备中,交叉导轨提供高稳定性和低噪音的运动支撑,确保设备的精准城乡效果。
2、在手术机器人、放射治疗设备等高精度医疗设备中,交叉导轨的高精度和稳定性也起到了关键作用,可提高手术的操作精度和安全性。
3、在检验类设备的加样运动系统中,在CT检查床、X光机等医疗设备中,交叉导轨实现高精度、平稳的直线运动。
交叉导轨不仅在医疗器械领域中有广泛的运用,在自动化生产领域、数控机床领域、半导体设备制造领域、航空航天领域、工业机器人等领域都具有广泛的运用。其高精度、高刚性和稳定性能,能够满足各种复杂工况下的运动要求,提高整体设备的性能和安全性,为现代制造业的发展提供了强大的支撑。

相关文章:

交叉导轨在医疗设备上的作用!
随着医疗器械行业的需求逐步增长,交叉导轨给医疗器械行业带来了广阔的发展前景。作为重要的精密传动元件,交叉导轨具有寿命长、高精度、高刚性、高耐腐蚀性和高稳定性等优点,满足精密仪器上对产品的高要求使用场景。 在医疗设备领域中交叉导轨…...

【云原生】Docker Compose 使用详解
目录 一、前言 二、Docker Compose 介绍 2.1 Docker Compose概述 2.2 Docker Compose特点 2.3 Docker Compose使用场景 三、Docker Compose 搭建 3.1 安装docker环境 3.2 Docker Compose安装方式一 3.2.1 下载最新版/如果不是最新可替换最新版本 3.2.2 设置权限 3.2.…...
通过LabVIEW提升生产设备自动化水平
现代制造业对生产设备的自动化水平提出了越来越高的要求。使用LabVIEW这一强大的图形化编程环境,可以显著提升生产设备的自动化程度,改善生产效率和产品质量。本文将详细分析如何通过LabVIEW改善生产设备的自动化水平,并提供具体的实施策略与…...
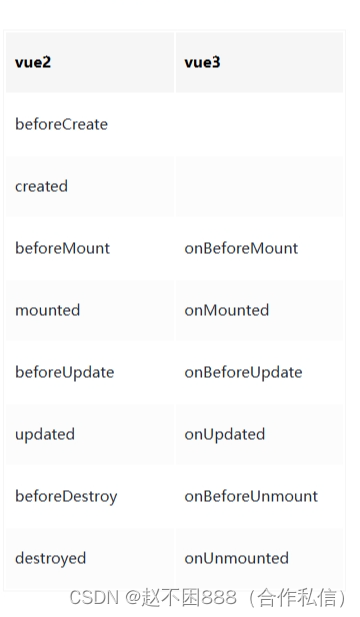
面试题vue+uniapp(个人理解-面试口头答述)未编辑完整....
1.vue2和vue3的区别(vue3与vue2的区别(你不知道细节全在这)_vue2和vue3区别-CSDN博客)参考 Vue3 在组合式(Composition )API,中使用生命周期钩子时需要先引入,而 Vue2 在选项API&am…...
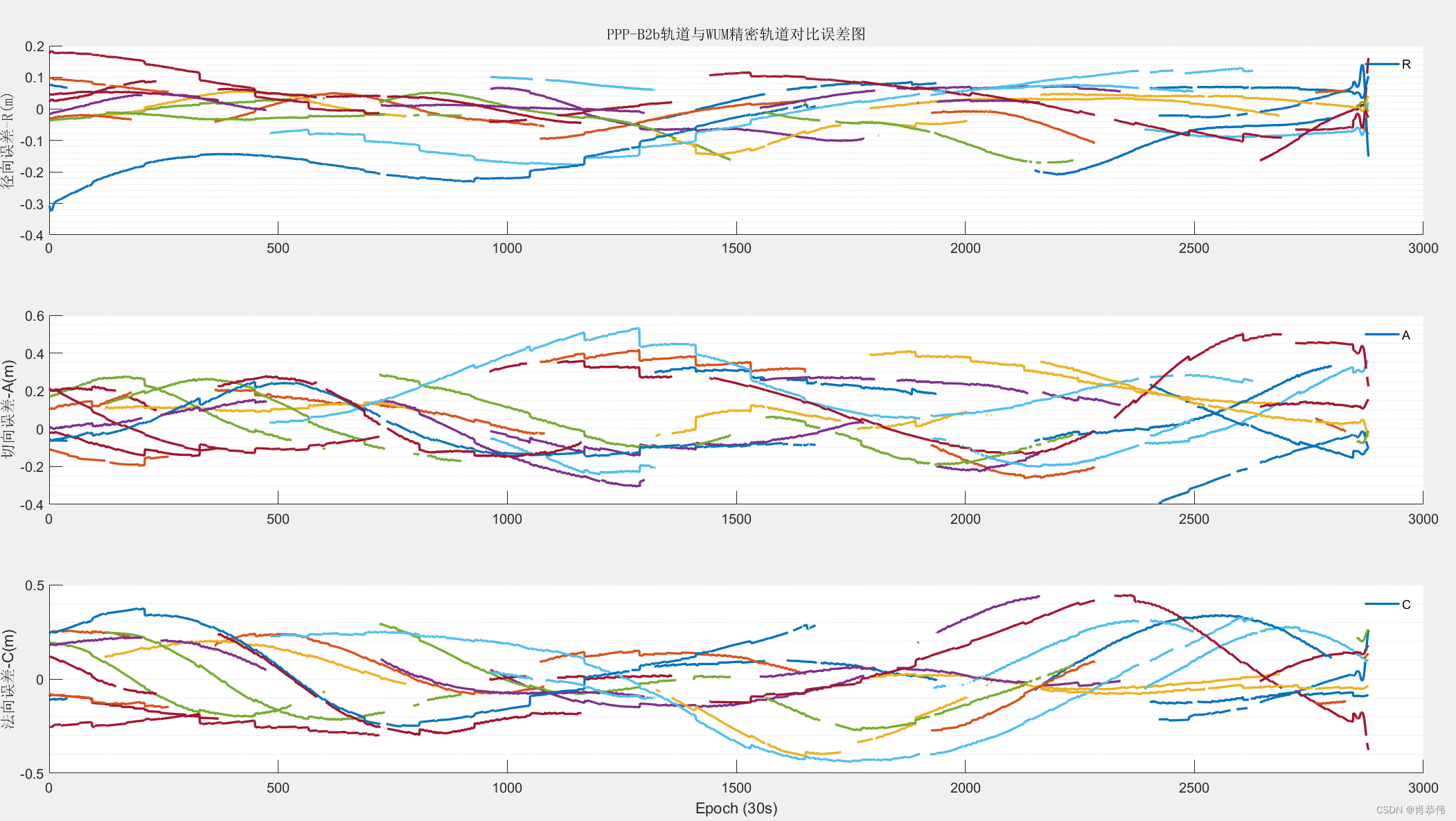
PPP-B2b精密产品使用注意事项及分析
1、因为在使用PPP-B2b进行定轨的时候,发的精密轨道产品是B3频点的,需要改正的卫星质心(Com)与SP3精密星历对比。 2、PPP-B2b产品吸收了电离层误差,因此电离层提取方面与IGS电离层完全无法对其。 3、由于PPP-B2b产品精…...
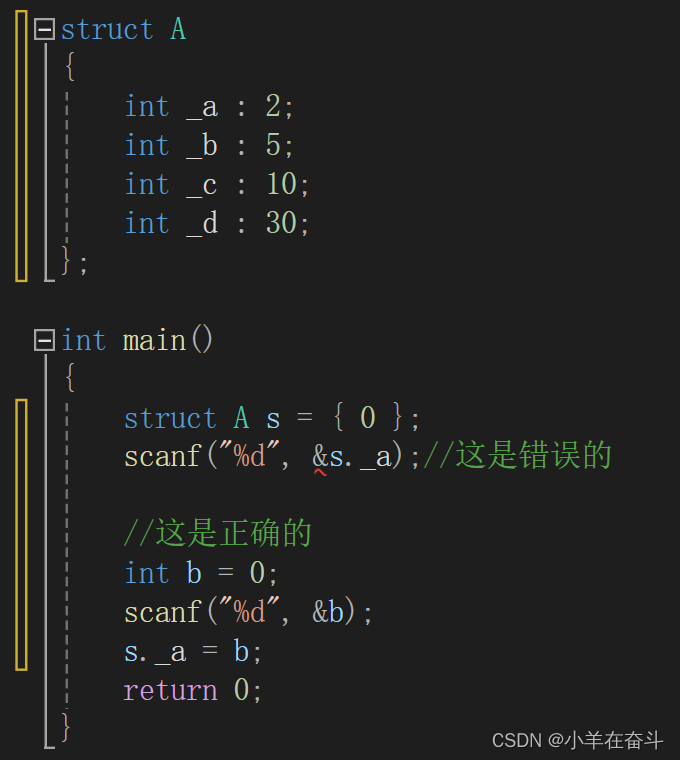
C语言(结构体)
Hi~!这里是奋斗的小羊,很荣幸各位能阅读我的文章,诚请评论指点,欢迎欢迎~~ 💥个人主页:小羊在奋斗 💥所属专栏:C语言 本系列文章为个人学习笔记,在这里撰写成文一…...
用法:深入解析与实战应用)
Python filter()用法:深入解析与实战应用
Python filter()用法:深入解析与实战应用 在Python编程中,filter() 函数是一个内置的高阶函数,它用于过滤序列,过滤掉不符合条件的元素,返回由符合条件元素组成的新列表。该函数在数据处理和筛选时非常有用࿰…...
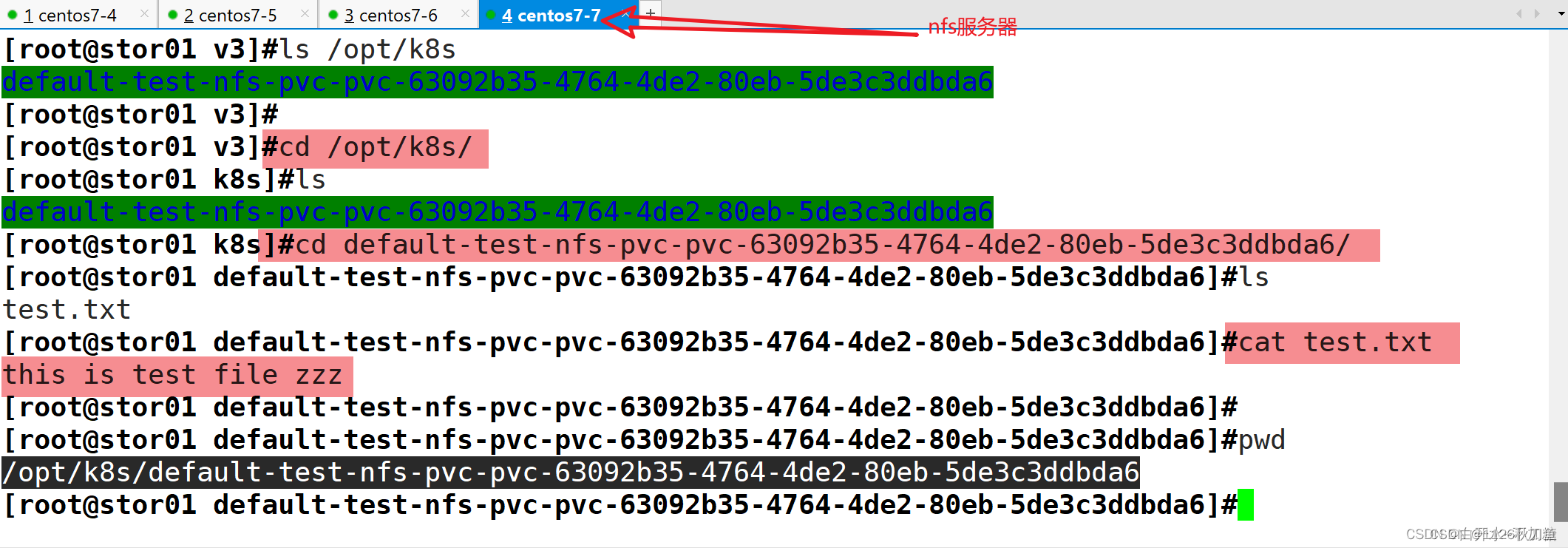
k8s集群的存储卷、pvc和pv
目录 简介 简介 PV 全称叫做 Persistent Volume,持久化存储卷。它是用来描述或者说用来定义一个存储卷的,这个通常都是由运维工程师来定义。 PVC 的全称是 Persistent Volume Claim,是持久化存储的请求。它是用来描述希望使用什么样的或者说…...

二分搜索树深度优先遍历
二分搜索树深度优先遍历 二分搜索树(Binary Search Tree,简称BST)是一种特殊的二叉树,它具有以下特性:对于树中的任意节点,其左子树中的所有元素都小于该节点的值,其右子树中的所有元素都大于该…...

ImportError: cannot import name ‘packaging‘ from ‘pkg_resources‘‘
参考自: [Bug]: ImportError: cannot import name packaging from pkg_resources (/usr/local/lib/python3.10/dist-packages/pkg_resources/__init__.py) Issue #15863 AUTOMATIC1111/stable-diffusion-webui GitHub ImportError: cannot import name packaging from pkg…...

灯塔歌曲音乐下载官网
灯塔歌曲音乐下载官网网址:www.dengtamp3.com 灯塔音乐下载上线以“用心服务,认真负责”为核心价值。 我们的团队是一个青春的团队,朝气蓬勃。我们采用最新的服务模式,以网为媒为广大客户提供服务,我们坚持以“用心&a…...

数据结构的归并排序(c语言版)
一.归并排序的基本概念 1.基本概念 归并排序是一种高效的排序算法,它采用了分治的思想。它的基本过程如下: 将待排序的数组分割成两个子数组,直到子数组只有一个元素为止。然后将这些子数组两两归并,得到有序的子数组。不断重复第二步,直到最终得到有序的整个数组。 2.核心…...

ubuntu使用Docker笔记
一、参考资料 1、B站视频 尚硅谷Docker实战教程 2、有心人整理的笔记 Docker笔记(周阳版) 3、菜鸟教程 Docker 教程 以下是本人的折腾实践。 二、Docker的安装 2.1、使用清华源安装docker,清华源官方教程。 本人是在ubuntu20.04下安装的…...

PHP编程入门:揭开Web开发的神秘面纱
PHP编程入门:揭开Web开发的神秘面纱 在数字化时代,PHP作为一种广泛使用的服务器端脚本语言,为Web开发领域注入了强大的活力。无论你是编程新手还是有一定经验的开发者,掌握PHP编程都将为你开启一扇通往Web开发新世界的大门。接下…...
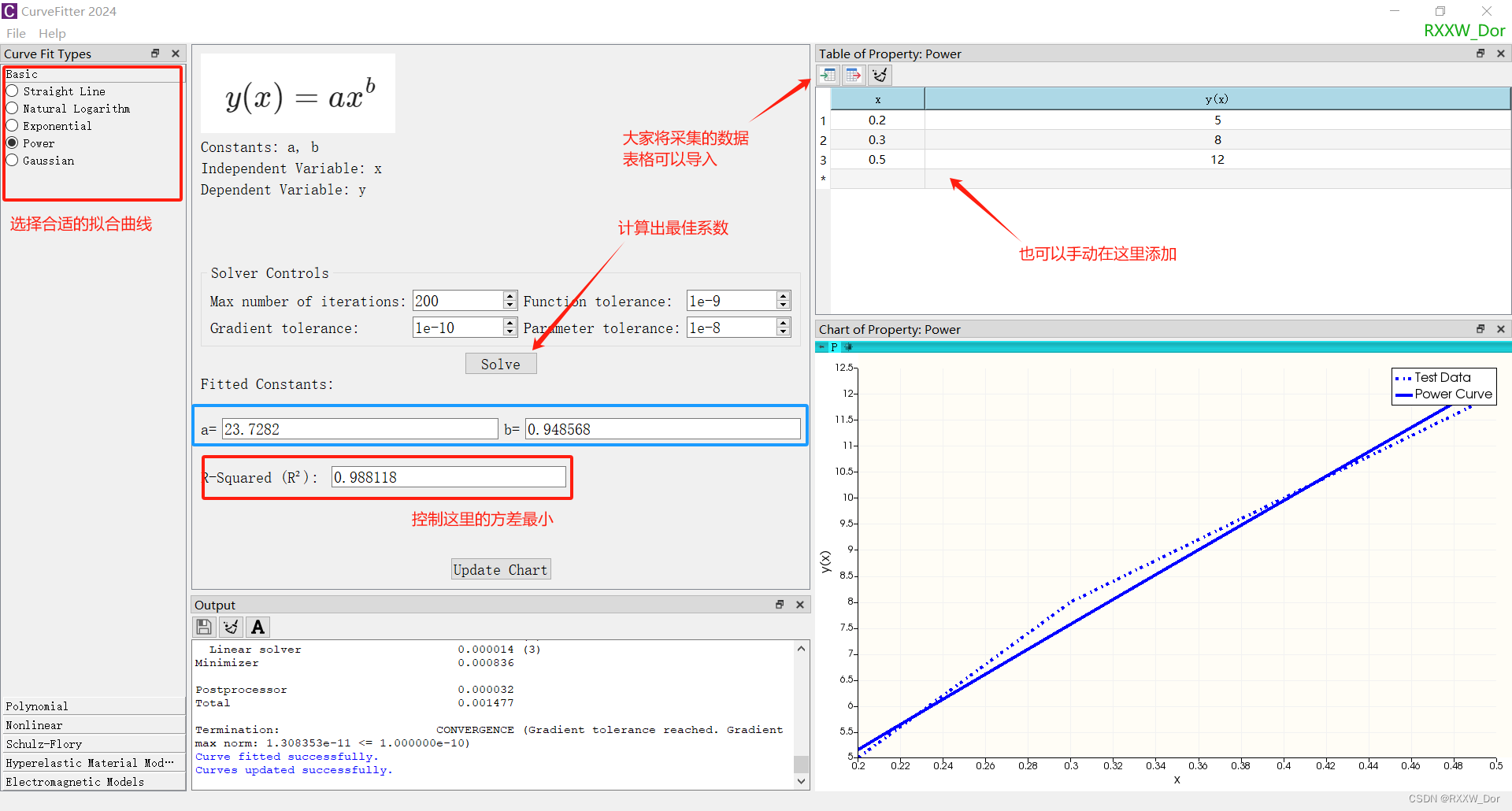
曲线拟合工具软件(免费)
曲线拟合是数据处理中经常用到的数值方法,本质是使用某一个模型(方程或者方程组)将一系列离散的数据拟合成平滑的曲线或者曲面,数值求解出对应的函数参数,大家可以利用MATLAB的曲线拟合工具箱也可以使用第三方的拟合软件,今天我们介绍Welsim免费的曲线拟合软件 1、MATLA…...
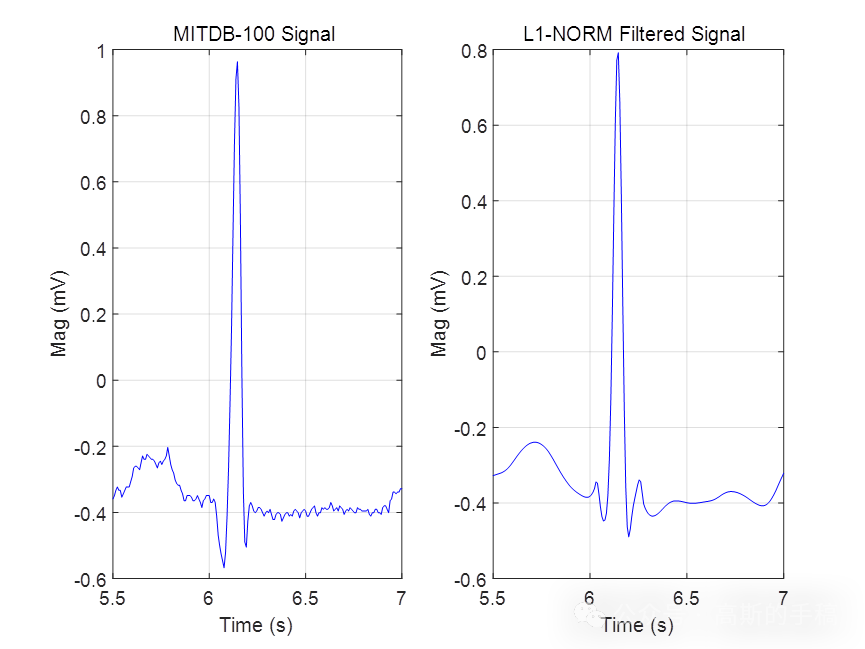
基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法(Matlab R2021B)
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量,它的非零系数相对较少,而Tikhonov正则化方法的解通常具有所有的非零系数。即:L2范数正则化方法的解通常是非稀疏的,并且解的结果在一…...
)
Bitbucket的原理及应用详解(一)
本系列文章简介: 在数字化和全球化的今天,软件开发和项目管理已经成为企业成功的关键因素之一。随着团队规模的扩大和项目的复杂化,如何高效地协同开发、管理代码和确保代码质量成为了开发者和管理者面临的重要挑战。Bitbucket作为一款功能强…...

企业级win10电脑下同时存在Python3.11.7Python3.6.6,其中Python3.6.6是后装的【过程与踩坑复盘】
背景: 需要迁移原始服务器的上的Python3.6.6+Flask项目到一个新服务器上, 新服务器上本身存在一个Python3.11.7, 所以这涉及到了一个电脑需要装多个Python版本的问题 过程: 1-确定新电脑版本【比如是32还是64位】 前面开发人员存留了两个包,是python-3.6.6.exe和pytho…...

泛微开发修炼之旅--03常用数据表结构讲解
文章链接:泛微开发修炼之旅--03常用数据表结构讲解...

MySQL8找不到my.ini配置文件以及报sql_mode=only_full_group_by解决方案
一、找不到my.ini配置文件 MySQL 8 安装或启动过程中,如果系统找不到my.ini文件,通常意味着 MySQL服务器没有找到其配置文件。在Windows系统上,MySQL 8 预期使用my.ini作为配置文件,而不是在某些情况下用到的my.cnf文件。 通过 …...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
