离散数学笔记_第一章:逻辑和证明(3)
1.3 命题等价式
- 1.3.1 逻辑等价式
- 1.3.2 条件命题和双条件命题的逻辑等价式
- 1.3.3 德·摩根律
- 1.3.4 可满足性
- 可满足的
- 不可满足的
- 可满足性问题的解
- 1.3.5析取范式(基本积之和),合取范式(基本和之积)
- 1.3.6合式公式
- 1.定义
- 2.等价转换成主析(合)取范式
1.3.1 逻辑等价式
定义1
永真式(重言式): 一个真值永远为真的复合命题。(无论其中出现的命题变量的真值是什么)
矛盾式(永假式): 一个真值永远为假的复合命题。
可能式: 既不是永真式也不是矛盾式的复合命题。
永真和矛盾的例子:
| p∧¬p | p∨¬p |
|---|---|
| 矛盾 | 永真 |
定义2
逻辑等价: 如果p↔q是永真式,则复合命题p和q称为是逻辑等价的。记作p≡q 或 p⇔q
注意不要写成等号 " = " !
注:符号 ≡ 和 ⇔ 不是逻辑联结词,p≡q 不是一个复合命题,而是代表 “p↔q是永真式” 这个语句
| 等价式 | 名称 |
|---|---|
| p∧T ≡ p ;p∨F ≡ p | 恒等律 |
| p∨T ≡ T ; p∧F ≡ F | 支配律 |
| p∨p ≡ p ;p∧p ≡ p | 幂等律 |
| ¬( ¬p) ≡ p | 双重否定律 |
| p∨q ≡ q ∨ p ;p∧q ≡ q ∧ p | 交换律 |
| (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) ; (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) | 结合律 |
| p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) ;p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) | 分配律(改变优先级) |
| ¬ ( p∧q ) ≡ ¬ p∨¬ q ;¬ ( p∨q ) ≡ ¬ p∧¬ q | 德·摩根律(去括号) |
| p ∨(p ∧ q) ≡ p ; p ∧(p ∨ q) ≡ p | 吸收律 |
| p∧¬p ≡ F ;p∨¬p ≡ T | 否定律 |
1.3.2 条件命题和双条件命题的逻辑等价式
→ ≡ ¬ ∧ ∨
| 条件命题的逻辑等价式(常用) |
|---|
| p → q ≡ ¬ p ∨ q |
| p → q ≡ ¬ q → ¬ p (原命题 ≡ 逆否命题 ) |
| (p → q) ∧ (p → r) ≡ p → (q∧ r) |
| (p → q) ∨ (p → r) ≡ p → (q∨ r) |
| 双条件命题的逻辑等价式 |
|---|
| p ↔ q ≡ (p → q) ∧ (q → p) |
| ¬( p ↔ q) ≡ p ↔ ¬ q |
| p ↔ q ≡ ¬ p ↔ ¬ q |
| p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q) |
1.3.3 德·摩根律
德·摩根律 (De Morgan’s law)
| 德·摩根律 | |
|---|---|
| ¬ ( p∧q ) ≡ ¬ p∨¬ q | ≡ p ↑ q |
| ¬ ( p∨q ) ≡ ¬ p∧¬ q | ≡ p ↓ q |
德·摩根律告诉我们如何取合取、析取的否定。
1.3.4 可满足性
可满足的
一个复合命题是可满足的,当且仅当存在一个对其变量的真值赋值使其为真。(即当它是一个永真式or可满足式时)
不可满足的
一个复合命题是不可满足的,当且仅当它的否定是可满足的。
可满足性问题的解
当我们找到一个特定的使得复合命题为真的真值赋值时(就证明了它是可满足 的),这样的一个赋值称为这个特定的可满足问题的一个解
1.3.5析取范式(基本积之和),合取范式(基本和之积)
1.3.6合式公式
1.定义
命题逻辑的合式公式 (wff, well‐formed formula)
• 1)一个命题变量 p 是一个 wff;
• 2)若 A 是 wff,则 (¬A) 也是 wff;
• 3)若 A, B 是 wff,则 (A∧B), (A∨B), (A→B), (A↔B) 也是wff;
• 4)当且仅当有限次使用上述规则得到的公式才是 wff。
上述定义是归纳定义:1)是归纳基始,2) 3)是归纳步,4)是最小化规则
命题逻辑的合式公式简称为公式或命题公式 。
⌛一般一个命题公式的真值是不确定的,只有当用确定的命题去取代命题
公式中的命题变元(变元 = 变量),或对命题变元进行真值指派时,命题公式才成为具有确定真值的命题。所以, 命题公式不是命题。
2.等价转换成主析(合)取范式
任何命题公式都可以等价地转换成它的主析取范式,也可以等价地转换成它的主合取范式
┐((P→Q)∧(R→P))∨┐((R→┐Q)→┐P)
≡ ┐((┐P∨Q)∧(┐R∨P))∨┐(┐(┐R∨┐Q)∨┐P)
≡ (┐(┐P∨Q)∨┐(┐R∨P))∨(┐┐(┐R∨┐Q)∧┐┐P)
≡ (P∧┐Q)∨(R∧┐P)∨((┐R∨┐Q)∧P)
≡ (P∧┐Q)∨(R∧┐P)∨(┐R∧P)∨(┐Q∧P)
≡ (P∧┐Q∧R)∨(P∧┐Q∧┐R)∨(R∧Q∧┐P)∨(R∧┐Q∧┐P)∨
∨(┐R∧Q∧P)∨(┐R∧┐Q∧P)∨(R∧┐Q∧P)∨(┐R∧┐Q∧P)
≡ (P∧┐Q∧R)∨(P∧┐Q∧┐R)∨(┐P∧Q∧R)∨(┐P∧┐Q∧R)∨(P∧Q∧┐R)
≡ m5∨m4∨m3∨m1∨m6 (主析取范式)
≡ M0∧M2∧M7 (主合取范式)
相关文章:
)
离散数学笔记_第一章:逻辑和证明(3)
1.3 命题等价式1.3.1 逻辑等价式 1.3.2 条件命题和双条件命题的逻辑等价式 1.3.3 德摩根律 1.3.4 可满足性 可满足的 不可满足的 可满足性问题的解 1.3.5析取范式(基本积之和),合取范式(基本和之积)1.3.6合式公式1…...

软件测试分类知识分享,第三方软件测试机构收费贵不贵?
软件测试可以很好的检验软件产品的质量以及规避产品上线之后可能会发生的错误,随着技术的发展,软件测试已经是一个完整且体系庞大的测试活动,不同的测试领域有着不同的测试方法、技术与名称,那么具体有哪些分类呢? 一、软件测试…...
爬虫(二)解析数据
文章目录1. Xpath2. jsonpath3. BeautifulSoup4. 正则表达式4.1 特殊符号4.2 特殊字符4.3 限定符4.3 常用函数4.4 匹配策略4.5 常用正则爬虫将数据爬取到后,并不是全部的数据都能用,我们只需要截取里面的一些数据来用,这也就是解析爬取到的信…...

【C++、C++11】可变参数模板、lambda表达式、包装器
文章目录📖 前言1. 可变参数模板1.1 万能模板:1.2 完美转发:1.3 可变参数模板的使用:1.4 emplace_back:2. lambda表达式2.1 lambda表达式的定义:2.2 lambda表达式的用法:2.2 - 1 捕捉列表的用法…...

外贸主机测评
一、俄罗斯vps 服务商: JUSTG: Home - Sun Network Company Limited LOCVPS: LOCVPS 全球云 - 十年老牌 为跨境外贸/远程办公/网站建设提供澎湃动力 JUSTHOST: justhost.ru RUVDS: Gcorelabs: 二、主机测评指标: 1、速度、延迟、丢包、路由测试…...

Meta CTO:Quest 2生命周期或比预期更久
前不久,Meta未来4年路线图遭曝光,泄露了该公司正在筹备中的一些AR/VR原型。除此之外,还有消息称Quest Pro或因销量不佳,而不再迭代。毫无疑问,Meta的一举一动持续受到行业关注,而面对最近的爆料,…...

Vector - CAPL - 文件处理函数
在当前平台化的趋势下,就算是协议层测试依然需要适配各种各样的项目,也需要处理各类型的文件,那我们如何对文件进行读取、写入、修改等类型的操作呢?今天我们就会介绍此类型的函数,主要适用于text、bin文件的处理。 打开文件 Open...

实力加持!RestCloud完成多方国产化适配,携手共建信创生态
近年来,随着数字化建设进入深水区,企事业单位对信息安全重视程度与日俱增,核心技术自主可控已成为时代呼唤,国产化浪潮日益汹涌澎湃。近日,RestCloud在国产化方面取得新进展,完成了全部产品线信创环境的多方…...

Unity 3D GUI教程||OnGUI TextArea 控件||OnGUI ScrollView 控件
OnGUI TextArea 控件 Unity 3D TextArea 控件用于创建一个多行的文本编辑区。用户可以在多行文本编辑区编辑文本内容。 该控件可以对超出控件宽度的文本内容实现换行操作。 TextArea 控件同样会将当前文本编辑区中的文本内容以字符串形式返回。 开发人员可以通过创建 Strin…...
Leetcode.828 统计子串中的唯一字符
题目链接 Leetcode.828 统计子串中的唯一字符 Rating : 2034 题目描述 我们定义了一个函数 countUniqueChars(s)来统计字符串 s中的唯一字符,并返回唯一字符的个数。 例如:s "LEETCODE",则其中 "L", "…...

Hibernate 相关特性
1. Hibernate一般使用hql进行查询,但也有sql执行的方法 Native sql 查询,。需要注意的是,使用Native SQL查询可能会破坏Hibernate的缓存机制,并可能导致性能问题 String sql "SELECT * FROM users WHERE age > :age"; Query …...

【研究生学术英语读写教程翻译 中国科学院大学Unit1-Unit8】
Unit1 Descartes Was Wrong 笛卡尔错了:“他人在,故我在” Unit2 Are we ready for the next volcanic catastrophe?我们准备好应对下一次火山灾难了吗? Unit3 Theorists,experimentalists and the bias in popular physics理论家,实验家和大众物理学的偏见 unit4 Magic Nu…...

ListView 控件的使用
第一步:找到ListView的控件通过findViewById 找到ListView的控件 ListView listView findViewById(R.id.listView);第二步:创建Bean类 得到set和get的方法解析获取的数据创建Bean类 得到set和get的方法public class Bean {String nanm""; pub…...
域控制器搭建以及成员加入
需要iso:windows server 2016软件使用:vmwarewindows server 2016系统搭建自己选iso,一直下一步就可以安装完成。(记得要设置密码)(密码要求大小写字母数字符号)等待就能安装完成。安装和配置Ac…...
利用 MLP(多层感知器)和 RBF(径向基函数)神经网络解决的近似和分类示例问题(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 1、径向基神经网络 径向基函数网络是由三层构成的前向网络:第一层为输入层,节点个数的能与输入的维数&…...
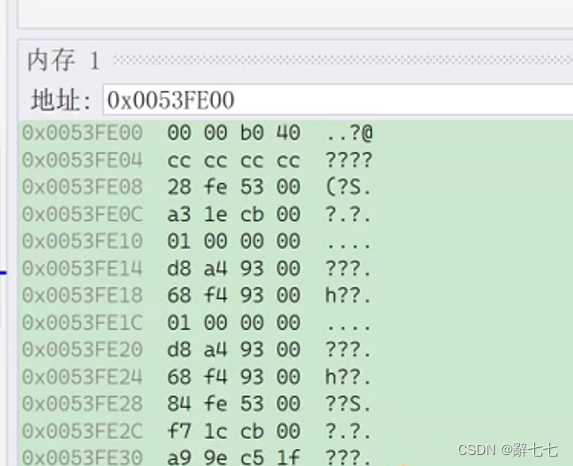
进阶C语言——数据的存储【详解】
文章目录1. 数据类型介绍1.1 类型的基本归类2. 整形在内存中的存储2.1 原码、反码、补码2.2 大小端介绍2.3 练习3. 浮点型在内存中的存储3.1 一个例子3.2 浮点数存储的规则1. 数据类型介绍 前面我们已经学习了基本的内置类型: char //字符数据类型 short //短整型 …...
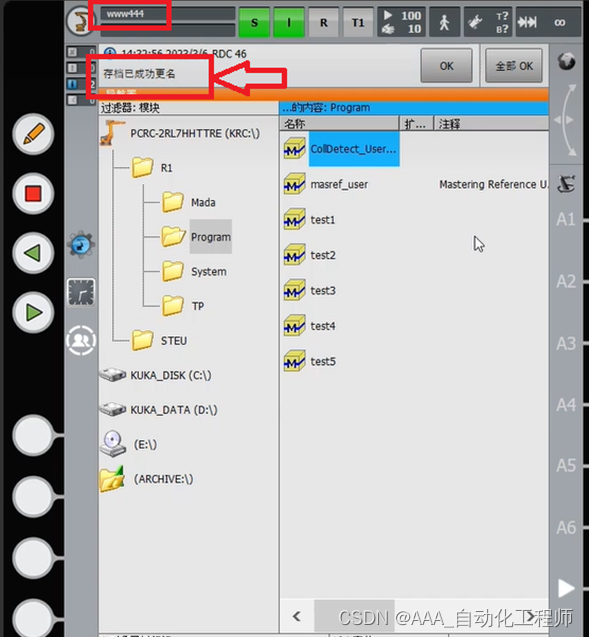
KUKA机器人修改机器人名称和IP地址的具体方法示例
KUKA机器人修改机器人名称和IP地址的具体方法示例 修改机器人名称 如下图所示,首先切换用户组到管理员,输入默认密码:kuka, 如下图所示,点击菜单键—投入运行—机器人数据, 如下图所示,此时可以看到机器人的名称为rrr445, 如下图所示,修改之后,点击左侧的“”…...
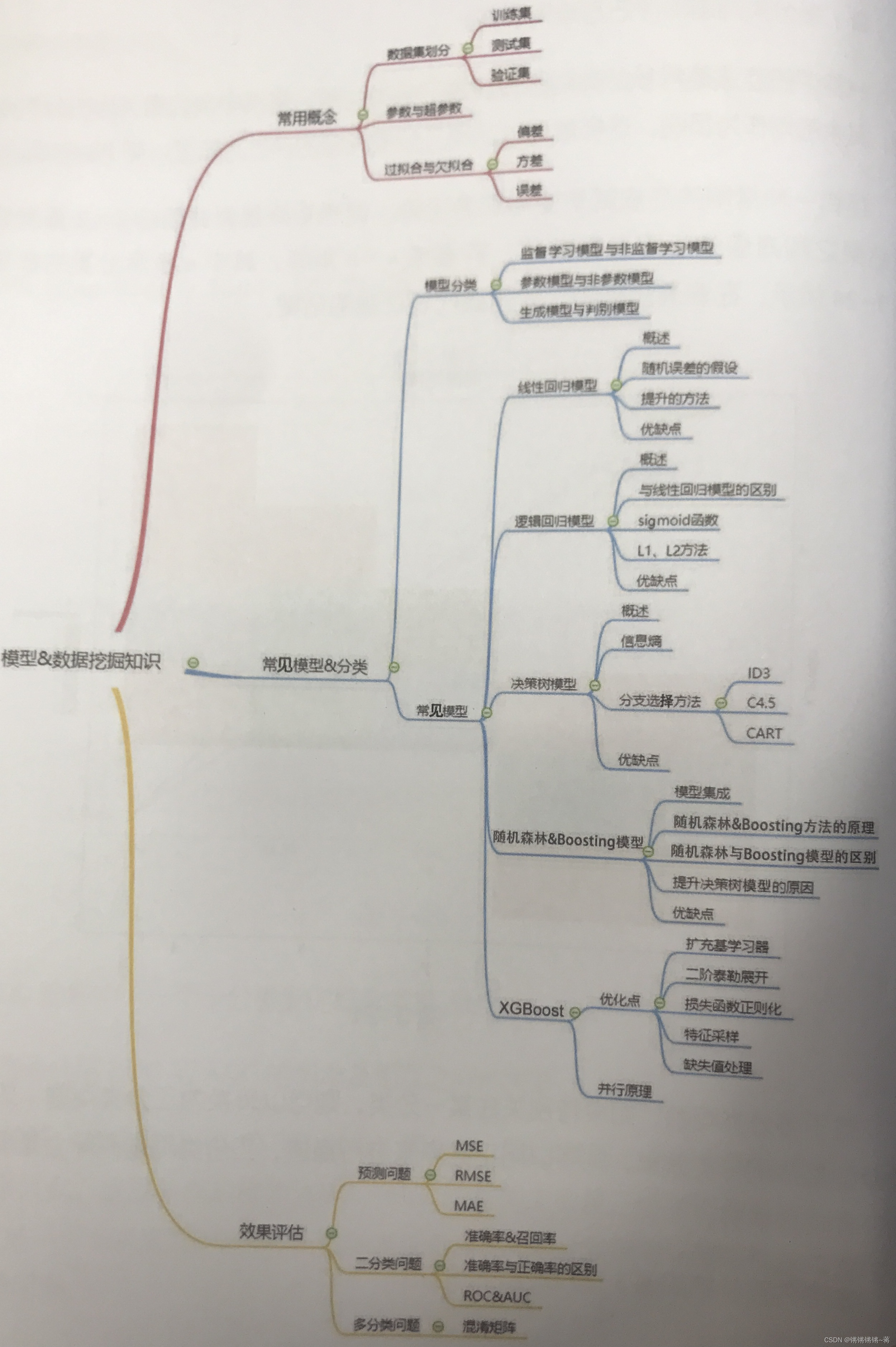
【数据分析师求职面试指南】必备基础知识整理
数据分析师基础知识统计 数据分析知识基础概念随机变量常用特征正态分布与大数定律、中心极限定律假设检验模型、数据挖掘知识常用概念数据集划分欠拟合过拟合模型分类方法常见模型介绍线性回归模型:逻辑回归模型决策树模型随机森林模型Boosting模型XGBoost模型模型…...
的原理与应用》)
《开关电源宝典 降压电路(BUCK)的原理与应用》
嗨,硬件攻城狮或电源工程师同行们,我想写本专门解析BUCK电源电路的书籍,以下是“前言”内容的部分摘录以及当前的目录,当前已经完成22万多字500多页了,即使如此,离真正出版书籍,还有很长的路要走…...

R语言基础(一):注释、变量
R语言用于统计分析和绘制图表等操作。不同于Java等其它语言,R用于统计,而不是做一个网站或者软件,所以R的一些开发习惯和其它语言不同。如果你是一个编程小白,那么可以放心大胆的学。如果你是一个有编程基础的人,那么需…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
