计算机中信息的表示和处理 整数和小数的二进制表示

• 现代计算机存储和处理的信息以二值信号表示，这些二进制数字称为位，为什么要用二进制来进行编码？因为二进制只有1和0两种状态，正好可以用高低电平来表示，同时可以数值之间可以方便的进行逻辑和算数运算，否则如果用人类容易理解的十进制编码，那机器如何识别这10个状态呢？比较困难
• 大多数计算机用8位的块(比特)，或者说1字节作为最小的可寻址的内存单位，而不是访问内存中单独的位。机器级程序将内存视为一个非常大的字节数组，称为虚拟内存(virtual memory)，内存中每一个字节都有一个唯一数字标识，称为它的地址(address)

整数

进制

• 二进制$(Binary)$后缀是$B$，十进制$(Decimal)$后缀是$D$，八进制$(Octal)$后缀是$O$，十六进制$(Hex)$后缀是$H$
• 这里相信读者对任意进制转十进制以及十进制转任意进制(整数和小数部分分开处理然后拼起来)并不陌生，简单说一下二进制和八进制或者十六进制的互相转化，比如下面这个十六进制数
  $$0x39A7F8$$
• 怎么把它转化成二进制数？最简单的办法就是一位一位转换，比如$3$可以转换成$(0011{)}_2$，$9$可以转化成$1001$这样转化下去，拼起来就可以得到结果如下
  $$001110011010011111111000$$
• 二进制转十六进制一个道理

字

• 在Windows系统中我们也许知道有32位和64位的区别，那么这个区别到底是什么呢？事实上，每台计算机都有一个字长(word size)，指明指针数据的标称大小(nominal size)，字长决定的最重要的系统参数就是虚拟地址空间的访问最大大小，也就是说，对于一个字长为$w$的机器而言，虚拟地址的范围就是$0-2^w-1$，程序最多访问$2^w$个字节，那么32位系统的虚拟地址空间就是$2^{32}$个字节，大概是4GB
• 那么问题来了，跨越多字节的程序对象如何处理呢？答案应该是使用地址来找到这个对象，同时还要知道如何在内存中排列这些字节。因为几乎所有的机器上多字节对象都被存储位连续的字节序列，对象的地址为所使用字节中最小的地址
• 有两种方法排列这些字节，要么从低到高，称为小端法(little endian)，要么从高到低，称为大端法(big endian)，这里的高低可以这样理解，比如数字123456，1属于高，6属于低。有时候这会造成问题，比如网络传输数据的时候，不同方法的机器可能导致传输字节反序，这需要注意，我们可以看下面这个例子

#include <bits/stdc++.h>using namespace std;typedef unsigned char *byte_pointer;void show_bytes(byte_pointer start, size_t len){size_t i;// unsigned intfor(int i=0;i<len;i++){printf(" %.2x", start[i]);// start是val的首地址，因为两个十六进制位占1个字节，所以输出两位}printf("\n");
}
int main(){int val = 0x87654321;byte_pointer valp = (byte_pointer) &val;// 取地址show_bytes(valp, 1);// 21show_bytes(valp, 2);// 21 43show_bytes(valp, 3);// 21 43 65return 0;
}

• 可以测试一下运行结果，小端法机器输出如上图
• 我们可以用C语言的运算符sizeof来确定对象使用的字节数

移位运算

• 默认读者使用过移位运算，大概知道怎么回事，C语言移位有左移和右移，左移就是末位补0，高位舍弃；右移有两种，算数右移和逻辑右移，但C语言没有明确规定，逻辑右移是在左端补0，算数右移是在左端补最高位的值，比如现在最高位是1，那就在左端全补1，也就是说算数右移不改变数的正负
• 而Java中规定明确，x>>k表示算数右移，x>>>k表示逻辑右移

无符号数和有符号数

• 假设一个整数数据类型有$w$位，我们可以把位向量写成$\vec{x}$，表示整个向量，那么整个数字就是$[x_{w-1},x_{w-2},\cdots ,x_0]$，表示向量中的每一位，所以对于一个无符号数有$$B2U_w(\vec{x})=\sum _{i=0}^{w-1}{x}_i{2}^i$$其中$B2U_w$表示$BinarytoUnsigned$，长度为$w$，这个函数是一个双射，意思就是正向一对一，反向也一对一，所以我们可以用每一个数表示一个状态，进行状态压缩
• 对于有符号数，一般计算机表示方式是补码形式，我们用函数$B2T_w(BinarytoTw{o}^{\prime }s-complement)$表示，补码编码的定义如下，对向量$\vec{x}=[x_{w-1},x_{w-2},\cdots ,x_0$]，有$$B2T_w(\vec{x})=-x_{w-1}{2}^{w-1}+\sum _{i=0}^{w-2}{x}_i{2}^i$$
• 有符号数的另外两种标准的表示方法是原码和反码，原码$(Sign-Magnitude)$的最高有效位是符号位，用来确定剩下的位是正权还是负权，有$$B2S_w(\vec{x})=(-1{)}^{x_{w-1}}\times (\sum _{i=0}^{w-2}{x}_i{2}^i)$$
• 反码$(On{e}^{\prime }sComplement)$表示的话，最高有效位的权比补码多了个1，表示如下$$B2O_w(\vec{x})=-x_{w-1}(2^{w-1}-1)+\sum _{i=0}^{w-2}{x}_i{2}^i$$
• 但是你会发现原码和反码在表示0的时候都有两种情况，原码是因为最高位表示符号，是不是1对于0无影响，反码是因为最高有效位权多了个1，导致所有位都是1的时候值变成了0
• 对于很多国内教材，讲到补码的时候会说，对于一个正整数，补码和原码相同(原码就是这个数转化成二进制)，对负整数来说，补码是原码取反+1，从上面的公式中可以轻松推出这一结论
• C语言中的强制类型转换非常简单，就是位表示不会改变，只是改变了解释这些位的方式，那么如果一个有符号的负数转化成一个无符号的数就可能变成一个大正数，如果位不够要进行扩展，扩展可能是零扩展也可能是符号扩展，这个和逻辑右移与算数右移比较类似，如果位太多要截断，这里书中有详细介绍，我就不求甚解了

加法运算

• 显然由于计算机字长和内存的限制，一个数字不能无限制的增大，否则就会失去它原本的意义，加法实际上就是超过部分舍掉就完事了，两个无符号数加法公式如下$$x+{}_w^{u}y=\{\begin{array}{llc}x+y,& x+y<2^w& 正常\\ x+y-2^w,& 2^w\le x+y<2^{w+1}& 溢出\end{array}$$
• 补码加法同理$$x+{}_w^{t}y=\{\begin{array}{llc}x+y-2^w,& 2^{w-1}\le x+y& 正溢出\\ x+y,& -2^{w-1}\le x+y<2^{w-1}& 正常\\ x+y+2^w,& x+y<-2^{w-1}& 负溢出\end{array}$$
• 上面的公式简单来说就是，你就直接加，超出位数就不要了，得到的答案就是运算结果

小数

定点表示

• 小数转化为二进制比较容易，对于整数部分，按照整数转化为二进制的方式进行转化；对于小数部分，通常采用的方法是乘$2$取整，直到符合的位数
• 这是定点表示的方法，但是对于类似$1\times 2^{100}$这样非常巨大的数字，我们不能够使用定点表示的方法，接下来看如何使用浮点表示

IEEE 浮点表示

• 浮点数对形如$V=x\times 2^y$的有理数进行编码，换句话说就是将小数转换为二进制表示，然后再对其进行编码，乘$2^y$是什么意思？就是二进制移位

IEEE浮点标准用$V=(-1{)}^s\times M\times 2^E$的形式来表示一个数

• 符号(sign)，s决定这个数是正数还是负数，而对于数值0的符号位解释作为特殊情况处理
• 尾数(significand)，M是一个二进制小数，它的范围是$1\sim 2-\epsilon$，或者是$0\sim 1-\epsilon$
• 阶码(exponent)，E的作用是对浮点数加权，这个权重是2的E次幂(可能是负数)

将浮点数的位表示划分为三个字段，分别对这些值进行编码，分为单精度(32位的float)和双精度(64位的double)

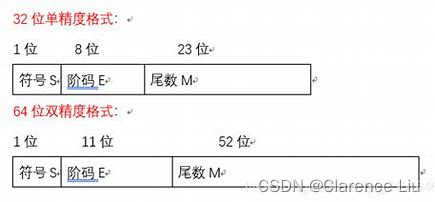
• 根据上图可以解决一个问题，那就是单精度和双精度数能精确到小数点后多少位，根据即将要讲到的规格化定义，尾数表示的是$2^{M+1}$，所以显然单精度能表示到$2^{24}=16777216$，这个数在$10^7$和$10^8$之间，排除掉最后一位的舍入问题，单精度能精确到小数点后$6$位；同理双精度能表示到$2^{53}=9007199254740992$，在$10^{16}$和$10^{17}$之间，所以能精确到小数点后$15$位

规格化和非规格化

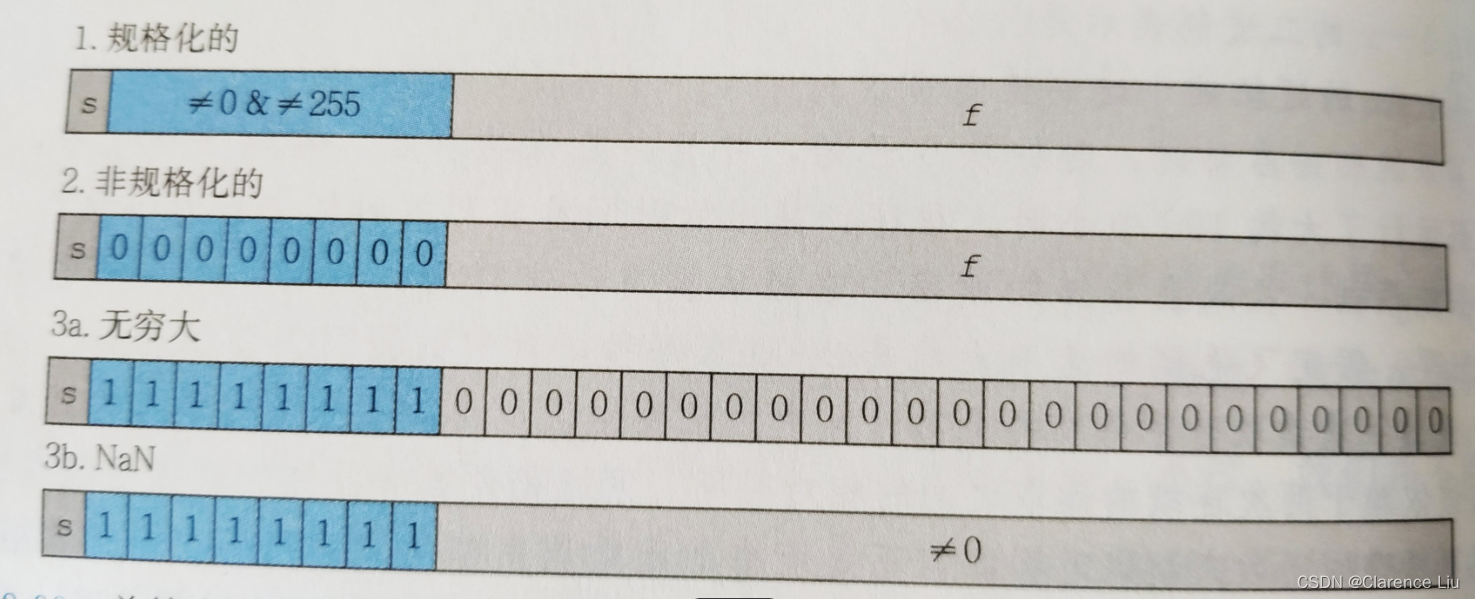
下面对上图进行一些解释

• 根据阶码，引入了规格化和非规格化的概念，如果阶码的所有二进制位不全为0，也不全为1，那么就说这个二进制小数是规格化的，但是在这种情况下，阶码字段被解释成以偏置(biased)形式表示的有符号整数，也就是说，阶码的值是$E=e-Bias$，其中$e$是无符号数，而$Bias$是一个等于$2^{k-1}-1$(单精度127，双精度1023)的偏置值。由此，指数的取值范围对于单精度是$-126\sim +127$，双精度是$-1022\sim +1023$，小数字段$frac$被解释为描述小数值$f$，这个$f$的范围是$[0,1)$，二进制表示为$0.f_{n-1}...f_1{f}_0$，正常情况下是这样，但是我们可以通过调整阶码$E$让这个二进制数变成$1.f_{n-1}{f}_{n-2}...f_0$，这样，这个开头的$1$不需要记录，就提高了1位的精度位，这就是规格化表示
• 对于非规格化，阶码域就全是0，阶码值是$E=1-Bias$，这样设置阶码值的意义是从规格化到非规格化能够平滑转换，而尾数的值是$M=f$，也就是小数字段的值，不包括隐含的开头的1，因为规格化数后面的二进制小数是1.几，所以没办法表示0，那么非规格化就可以表示$0.0$，但是如果符号位是1的话，得到的就是$-0.0$，IEEE浮点格式对这两种数也有它自己的规定，另外一个就是逐渐下溢，可以表示非常接近于0.0的数
• 当阶码所有位都是1的时候，如果小数域都是0，那么这个数就表示无穷，不都是0就表示NaN(Not a Number)，如果有两个非常大的数相乘，那么得到的结果就会是inf，也就是无穷

舍入

• 因为浮点数只能近似表示实数，所以需要考虑如何进行舍入，一般有四种舍入方式，下面以舍入到整数为例

1. 向上舍入，很简单，比如1.2，向上舍入就是2，如果是-1.2向上舍入就是-1，就是往大了取
2. 向下舍入，和第一个相反，1.2向下舍入是1，-1.2向下舍入是-2
3. 向零舍入，1.2向零舍入就是1，-1.2向零舍入就是-1
4. 向偶数舍入，这个比较特殊，它将数字向上或者向下舍入，使得最终结果是距离这个数字最近的数；如果距离相等则舍入到有效数字的最后一位是一个偶数的数，比如说1.4会舍入到1，因为1.4处于1和2之间，而它距离1比较近，所以舍入到1；如果是1.5，因为它距离1和2一样近，这个时候因为1是个奇数，所以需要舍入到2，如果是2.5则向下舍入到2。那么为什么要引入这样奇怪的方式呢？主要是避免大量的向上或者向下取整带来的统计偏差，相当于取了一个平均值

浮点运算

1. 对阶，目的是让两个操作数的小数点位置对齐，使得两个数的阶码相等，这样我们先求阶差，然后以小阶向大阶对齐的原则，具体操作过程就是尾数右移，给阶码腾出空间，这样尾数的低位数就会丢失，这也就说明了为什么要以小阶向大阶对齐，如果返回来那么势必要左移，这样尾数的高位就要丢失，产生错误，因为低位丢失误差较小，高位丢失误差很大
2. 尾数求和，将对阶之后的尾数按照定点数加(减)运算规则运算。运算后的尾数不一定是规格化的，因此，浮点数的加减运算需要进一步进行规格化处理
3. 规格化，IEEE 754规格化尾数的形式是$\pm 1.$x$\cdots$x，但是尾数加减之后不一定能得到这种情况，可能小数点之前好几位，或者小数点前面是0，这时候需要进行规格化处理，具体方法是左规和右规，直到最高位1移动到小数点前作为隐藏位，这个在前面的规格化中已经说过
4. 舍入，因为前面对尾数进行了一些右移操作，可能会造成一些浮点误差，为了保证运算精度，一般将低位移出的两位保留下来，参加中间过程的运算，最后将运算结果进行舍入，还原表示成IEEE 754格式，常见的舍入方法有0舍1入法(舍去的尾数最高位如果是1则对新的尾数+1，否则不动，但是这样可能使尾数溢出，此时需要再做一次右规)、恒置1法(只要因移位而丢失的位中有1就把尾数末位置1)和截断法(恒舍法)(直接截取所需位数，丢弃后面的所有位)
5. 溢出判断，看指数是不是超过了最大允许值或者低于最小允许值，如果是这样的话就发生了溢出，进行相应的处理

阿贝尔群：又称交换群或加群，它由自身的集合G和二元运算*组成，它除了满足一般的群公理，即运算的结合律、G有单位元、所有G的元素都有逆元之外，还满足交换律公理。因为阿贝尔群的群运算满足交换律和结合律，群元素乘积的值与乘法运算时的次序无关，换句话说对于任意的$a,b\in G$，都有$ab=ba$，或者说$a+b=b+a$

• 可以看出整数加法形成了一个阿贝尔群，而浮点数加法由于可能溢出到无穷大并不满足结合律所以不是一个阿贝尔群，这个需要注意

未完待续