蒙层(css)
如何在 Vue 中实现一个包含图像和蒙层效果的组件?这个组件根据某个条件显示或隐藏蒙层,用于表示图像是否已读。

1. 创建基础模板
首先,我们在模板中使用 div 包裹我们的图像组件 GraphImage,并为最外层 div 设置 position: relative。
<div style="position: relative"><GraphImage :regNo="item.regNo" :showList="false" :zoom="true":modalWidth="400" :height="200" />//此处是图片</div>2. 添加条件渲染的蒙层
接下来,我们使用 Vue 的条件渲染 v-if 指令,在满足条件时显示蒙层
<div v-if="item.readFlag == '1'" class="overlay">已读</div>这段代码确保只有当 item.readFlag 等于 '1' 时,蒙层才会显示。
3. 定义蒙层样式
最后,我们添加蒙层的 CSS 样式,使其覆盖图像并显示居中的“已读”文字。
.overlay {position: absolute;top: 0;left: 0;width: 100%;height: 100%;background-color: rgba(128, 128, 128, 0.5); /* 半透明黑色蒙层 */display: flex;align-items: center;justify-content: center;color: white;z-index: 1;font-size: 20px;font-weight: bold;
}
相关文章:

蒙层(css)
如何在 Vue 中实现一个包含图像和蒙层效果的组件?这个组件根据某个条件显示或隐藏蒙层,用于表示图像是否已读。 1. 创建基础模板 首先,我们在模板中使用 div 包裹我们的图像组件 GraphImage,并为最外层 div 设置 position: relat…...
SpringBoot前端URL访问本地磁盘文件
SpringBoot前端通过 URL访问本地磁盘文件,其实就是 SpringBoot访问web中的静态资源的处理方式。 SpringBoot 访问web中的静态资源:https://blog.csdn.net/qq_42402854/article/details/90295079 首先,我们知道浏览器访问本地磁盘文件的方式为…...

【WP】猿人学2_js混淆_动态cookie
https://match.yuanrenxue.cn/match/2 抓包分析 根据发包加密参数在cookie中 删除cookie带的m参数,重新点击其他页面,然后使用Fiddler抓包 第一个包请求没有携带m,但是后面的请求是附带了m了,所以m就是在此之间生成 查看不带…...
基于springboot实现民族婚纱预定系统项目【项目源码+论文说明】
基于springboot实现民族婚纱预定系统的设计演示 摘要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本民族婚纱预定系统就是在这样的大环境下诞生,其可…...
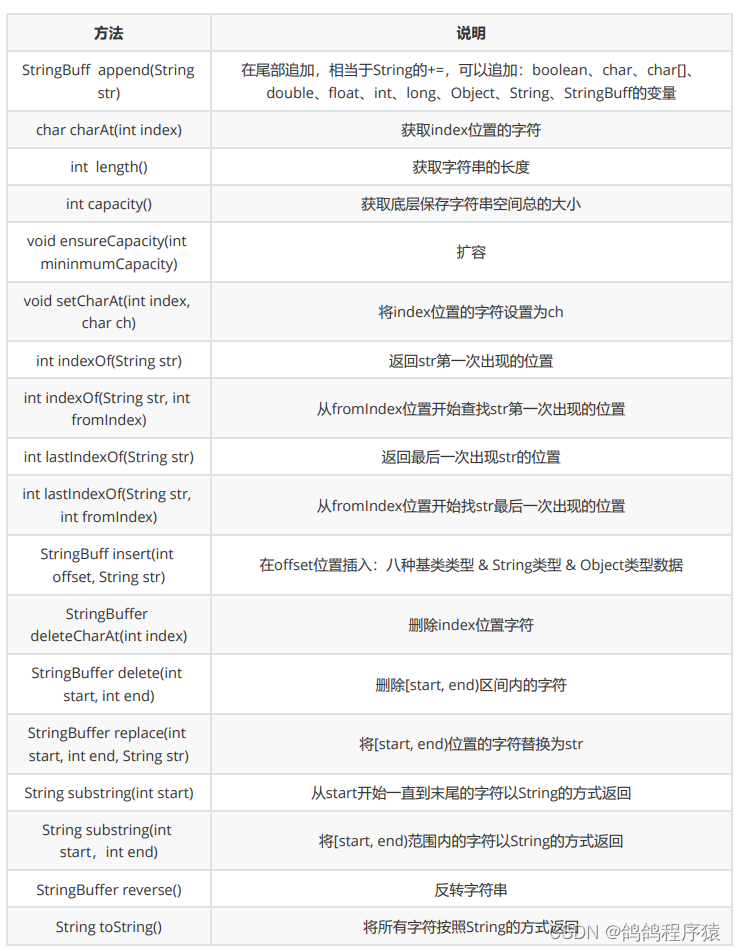
String常用操作
String常用方法 构造字符串 常用的构造字符串有3种: 1.直接赋值String s "abcd"; 2.实例化调用构造方法String s new String("abcd"); 3.实例化传字符数组 char[] ch {a,b,c,d}; String s new String(ch);字符串比较 比较 比较的是两个…...

git: 批量删除分支
环境: window11git version 2.42.0git-bash.exe window环境下: 1. 批量删除本地 git branch |grep xxx |xargs git branch -D比如: 想批量删除本地含有 release 关键字的分支: 2. 批量删除远程 git branch -r | grep xxxx | …...

【第5章】SpringBoot实战篇之登录模式切换
文章目录 前言一、接口扩展1. LoginStorage2. LocalLoginStorage3. RedisLoginStorage4. 参数配置 二、登录相关接口改动1.登录接口2. 登录拦截器 总结 前言 前面分别介绍了本地Map和redis存储用户登录信息,但是第二天我登录就出现问题了,因为我Redis部…...

2024最新华为OD算法题目
在一个机房中,服务器的位置标识在 n*m 的整数矩阵网格中,1表示单元格上有服务器,0 表示没有。如果两台服务器位于同一行或者同一列中紧邻的位置,则认为它们之间可以组成一个局域网。请你统计机房中最大的局域网包含的服务器个数。 输入描述 第一行输入两个正整数,n和m,…...

Redis集群方案有哪些?
今天咱们来聊聊Redis集群方案,想象一下Redis是个超级大的储物柜,里面放满了你各种各样的宝贝(数据)。但随着宝贝越来越多,一个储物柜不够用了,这时候我们就得想方设法扩大空间,还要保证找东西依…...

数字影像产业园的三大赋能:科技、创新与无限可能
数字影像产业园作为文创产业的重要载体,以科技为核心驱动力,不断推动产业的技术革新和升级。 园区内汇聚了最前沿的数字技术资源,高清摄影设备、虚拟现实技术、人工智能应用等尖端科技在这里得到广泛应用,不仅提升了生产效率&…...
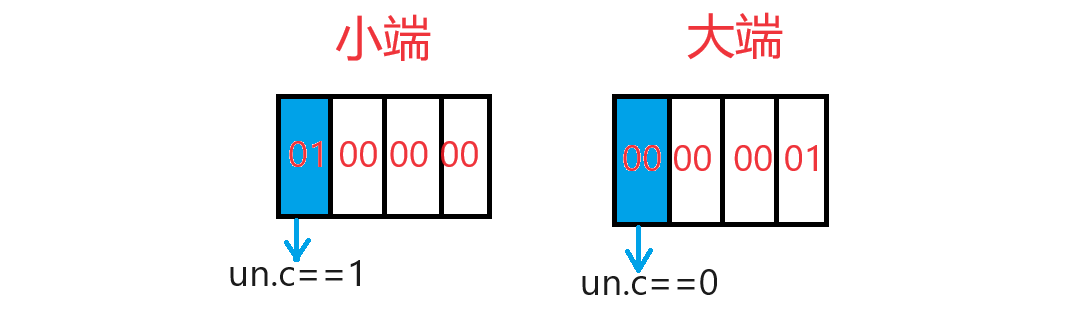
枚举(enum)+联合体(union)
枚举联合 一.枚举类型1.枚举类型的声明2.枚举类型的优点3.枚举类型的使用 二.联合体1.联合体类型的声明2.联合体的特点3.相同成员的结构体和联合体对比4.联合体大小的计算5.联合体的练习(判断大小端)6.联合体节省空间例题 一.枚举类型 1.枚举类型的声明…...

postman教程-15-前置脚本
上一小节我们学习了Postman生成随机数的方法,本小节我们讲解一下Postman前置脚本的使用方法。 Postman中的前置脚本(Pre-request Script)允许你在发送请求之前运行JavaScript代码。这可以用于修改请求头、查询参数、请求体等,或者…...

AIGC会带来失业潮吗?紧紧跟时代第一步,如何学习AIGC
会,但AI淘汰的始终是跟不上时代的人。 现在很多公司都有AI培训,不仅GPT,还有Midjourney、Stable DIffusion等一系列AI工具。 像我们公司虽然今年招的少,但也会对新招的应届生统一进行AI培训。 用任正非先生的话来说就是&#x…...
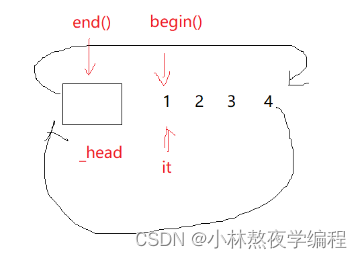
C++第二十四弹---从零开始模拟STL中的list(上)
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1、基本结构 2、基本函数实现 2.1、默认构造函数 2.2、尾插数据 3、迭代器的封装 3.1、迭代器的基本结构 3.2、迭代器重载函数的实现 4、迭…...
关于社情民意调查研究的内容)
大宋咨询(深圳社情民意调查)关于社情民意调查研究的内容
社情民意调查内容,是一项至关重要的社会研究活动,它涵盖了社会生活的方方面面,通过深入了解民众的需求、态度和看法,为决策提供了宝贵的参考依据。 首先,社会经济状况是社情民意调查不可或缺的一部分。这包括了对当地…...
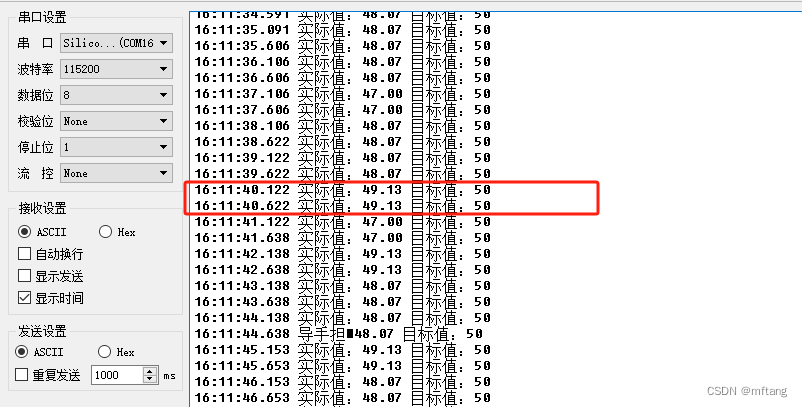
PID算法在电机速度控制上的应用
目录 概述 1 系统硬件框架 1.1 框架介绍 1.2 硬件实物图 2 STM32Cub生成工程 2.1 软件版本信息 2.2 配置参数 编辑2.3 生成项目 3 PID算法实现 3.1 概念 3.2 代码实现 4 其他功能实现 4.1 设置电机速度 4.2 PID算法控制电机 4.3 功能函数的调用 5 测试 5.1 …...

埃隆·马斯克 - 从梦想家到改变世界的企业家
埃隆马斯克 - 从梦想家到改变世界的企业家 本文内容是埃隆马斯克传的重点章节精华提炼,介绍了马斯克传奇一生 参考资料内容:埃隆马斯克传&造梦者埃隆马斯克 参考资料在文末获取,关注我,分享优质前沿资料(IT、运…...

微信小程序长图片自适应
/*wxss中的代码*/ .image-container { display:flex;width: 100%; /* 或其他需要的宽度 */ /* margin-bottom: 10px; //图片之间的间距 */height: auto; } 核心:要真正自适应,就要在wxml中加入固定宽度style“width:750rpx” /*wxml中的代码*/ &l…...

elasticsearch hanlp 插件安装操作
elasticsearch hanlp 插件安装操作 下载 hanlp 插件上传hanlp插件到elasticsearch服务器安装hanlp插件kibana测试 下载 hanlp 插件 这里大家根据自己对应的 elasticsearch 版本下载匹配版本的 hanlp 插件,由于 hanlp 及 elasticsearch 各个版本之间差别较大&#x…...

为什么进程和线程 ID 总是 4 的倍数?
如果您研究下任务管理器中的的进程 ID (PID),则你会发现这样一个规律:它们都是 4 的倍数。 基于 Windows NT 内核的操作系统上,不止是进程 ID,实际上,线程 ID (TID) 也遵守这样的规律:也即它们都是 4 的倍…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...
