力扣 48.旋转图像
题目描述:
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
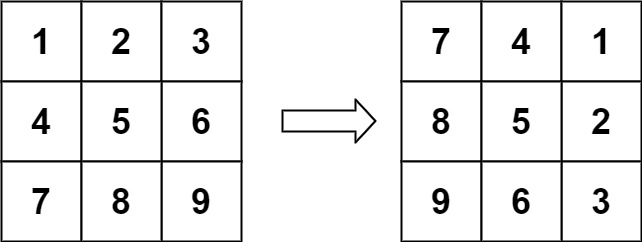
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
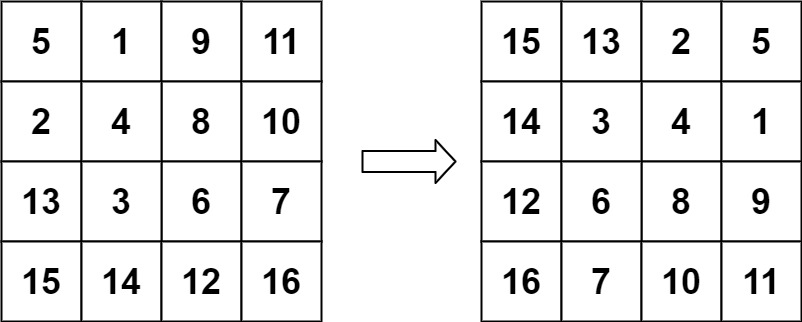
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
题解1:
最原始的做法,通过对每一行进行旋转进行找规律,发现有如下的公式:
matrix[j][n - 1 - i] = matrix[i][j];但是如果直接通过遍历数组来进行该公示的应用,那么之前已经置换过的位置会影响没有置换过的位置,因此还需要将原始数组保存起来,进行置换的时候 就将辅助数组的元素放置在原始数组的对应位置,这样就避免了原始数组被覆盖的可能。
代码实现:
public static void rotate(int[][] matrix) {int n = matrix.length;int[][] tmp = new int[n][];for (int i = 0; i < n; i++) {tmp[i] = matrix[i].clone();}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {matrix[j][n-i-1] = tmp[i][j];}}}知识点:
1、二维数组一整行进行拷贝复制:
tmp[i] = matrix[i].clone();
这样做的的问题:空间复杂度很大,考虑是否可以实现原地反转,即就在当前数组上进行翻转。
题解2 :
通过尝试发现,如果每次只取前n/2行和(n+1)/2行的这一片元素进行旋转就不会产生原始没用放到正确位置上的元素被覆盖的情况,比如说,现在就取四个角, A B
C D
旋转之后,A->B B->D D->C C->A,实现的时候逆着来,即先重置A位置为C,再重置C位置为D,以此类推,但是需要先保存A位置的初始值,这样才能将B位置置为A。这样实现的旋转是不会产生元素覆盖的。
代码实现:
public static void rotate2(int[][] matrix) {int n = matrix.length;for (int i = 0; i < n/2; i++) {for (int j = 0; j < (n+1)/2; j++) {int tmp = matrix[i][j];matrix[i][j] = matrix[n-1-j][i];matrix[n-1-j][i] = matrix[n-1-i][n-1-j];matrix[n-i-1][n-1-j] = matrix[j][n-1-i];matrix[j][n-1-i] = tmp;}}}反思:这样的想法是有考虑到的,但是由于不知道中间的元素要具体怎样旋转而没有深入思考, 其实如果能尝试写一下旋转公示的话,应该就能看出来其实中间的元素也和外围元素有一样的公式。但是取n/2和n+1/2进行旋转我也是想不到的,总结一下经验只能。
相关文章:

力扣 48.旋转图像
题目描述: 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 1: 输入:matrix [[1,2,3],…...

前端角色负责人岗
定位: 有效搭建、领导、优化一个自驱力强的前端团队,通过制度和工具把控质量和提高团队的生产力。 素质要求: 资深的技术专家且在流程规范、技术上自成体系;团队基础建设和持续集成方面需要有丰富的经验;具备组织管…...

git根据历史某次提交创建新分支
有时候项目在做版本管理的时候,忘记了创建某次版本的分支,而直接在主分支上进行开发了,这个时候,想要对某次提交单独拉出来一个版本分支,就需要用到这个功能: git checkout -b 新分支名 某次提交的id 找到…...

如何评价GPT-4o?GPT-4o和ChatGPT4.0的区别是啥呢?
如何评价GPT-4o? GPT-4o代表了人工智能领域的一个重要里程碑,它不仅继承了GPT-4的强大智能,还在多模态交互方面取得了显著进步。以下是几个方面的分析: 技术特点 多模态交互能力:GPT-4o支持文本、音频和图像的任意组合输入与输出…...
病理级Polymer酶标二抗IHC试剂盒上线!
免疫组织化学 Immunohistochemistry,lHC 是利用抗体与抗原特异性识别原理,对组织样本中的抗原进行定位/定性分析的实验技术。组织切片保留了样品的解剖学结构特征,从而可以高分辨率地显现蛋白在细胞,甚至细胞器中的定位。基于以上特性&…...

动态规划(多重背包问题+二进制优化)
引言 多重背包,相对于01背包来说,多重背包是每个物品会有相应的个数,最多可以选那么多个,因而对于朴素多重背包,需要在01背包的基础上,再加一层物品的循环 朴素多重背包例题 P2347 [NOIP1996 提高组] 砝…...

AI学习指南机器学习篇-逻辑回归正则化技术
AI学习指南机器学习篇-逻辑回归正则化技术 在机器学习领域,逻辑回归是一种常见的分类算法,它常用于处理二分类问题。在实际的应用中,为了提高模型的泛化能力和降低过拟合风险,逻辑回归算法通常会使用正则化技术。本文将介绍逻辑回…...

Django按照文章ID删除文章
重点是‘文章的ID’作为参数,如何在各个部分传递。 1、在视图函数部分 login_required def article_list(request):articles ArticlePost.objects.filter(authorrequest.user)context {articles: articles, }return render(request, article/column/article_lis…...

Java | Leetcode Java题解之第136题只出现一次的数字
题目: 题解: class Solution {public int singleNumber(int[] nums) {int single 0;for (int num : nums) {single ^ num;}return single;} }...
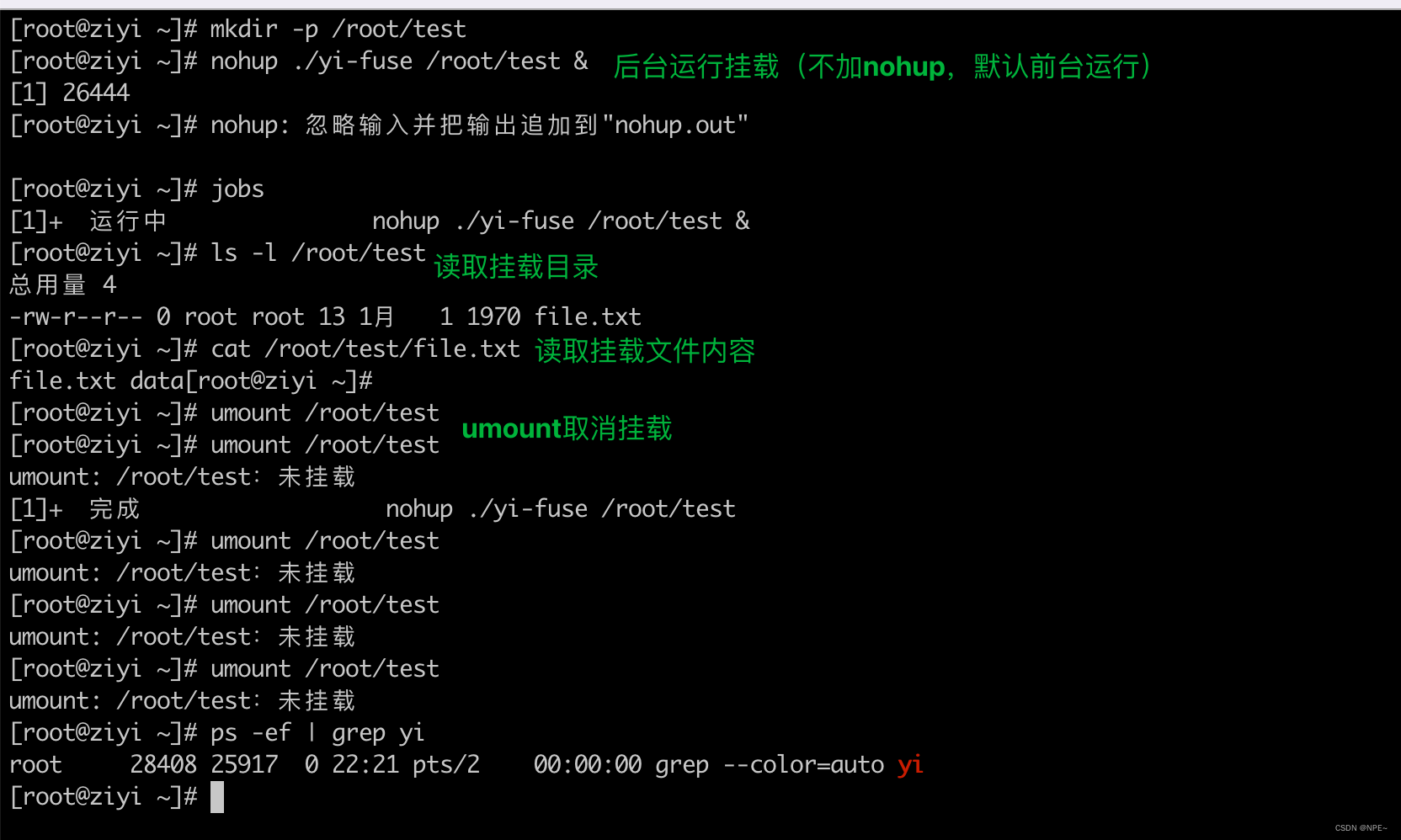
文件系统小册(FusePosixK8s csi)【1 Fuse】
文件系统小册(Fuse&Posix&K8s csi)【1 Fuse:用户空间的文件系统】 Fuse(filesystem in userspace),是一个用户空间的文件系统。通过fuse内核模块的支持,开发者只需要根据fuse提供的接口实现具体的文件操作就可以实现一个文…...

Bootstrap 环境安装
Bootstrap 环境安装 Bootstrap 是一个流行的前端框架,用于快速开发响应式和移动设备优先的网站。在开始使用 Bootstrap 之前,您需要安装相应的环境。本文将指导您如何安装 Bootstrap 环境。 1. 环境要求 在开始之前,请确保您的计算机上已安装以下软件: Node.js:Bootstr…...

GWT 与 Python App Engine 集成
将 Google Web Toolkit (GWT) 与 Python App Engine 集成可以实现强大的 Web 应用程序开发。这种集成允许你使用 GWT 的 Java 客户端技术构建丰富的用户界面,并将其与 Python 后端结合在一起,后端可以运行在 Google App Engine 上。 1、问题背景 在 Pyt…...

golang的函数为什么能有多个返回值?
在golang1.17之前,函数的参数和返回值都是放在函数栈里面的,比如函数A调用函数B,那么B的实参和返回值都是存放在函数A的栈里面,所以可以轻松的返回多个值。 其他的编程语言大都使用某个寄存器来存储函数的返回值。 但是从golang…...

一次 K8s 故障诊断:从 CPU 高负载到存储挂载泄露根源揭示
一、背景 现代软件部署中,容器技术已成为不可或缺的一环,在云计算和微服务架构中发挥着核心作用。随着容器化应用的普及,确保容器环境的可靠性成为了一个至关重要的任务。这就是容器SRE(Site Reliability Engineering,…...
)
python大作业:实现的简易股票简易系统(含源码、说明和运行截图)
实现一个简单的股票交易模拟系统。该系统将包括以下几个部分: 数据处理:从CSV文件中读取股票数据。 股票交易算法:实现一个简单的交易策略。 命令行界面(CLI):允许用户查看股票数据和进行交易。 数据持久化:将用户的交易记录和当前资金存储在数据库中。 为了简化这个示例…...

python-NLP常用数据集0.1.012
XNLI数据集 用户语言翻译和跨语言分类的语料库 官网地址:https://github.com/facebookresearch/XNLI下载地址:https://dl.fbaipublicfiles.com/XNLI/XNLI-1.0.zip注意事项:数据集有json格式的,和txt格式的数据格式 txt格式 la…...
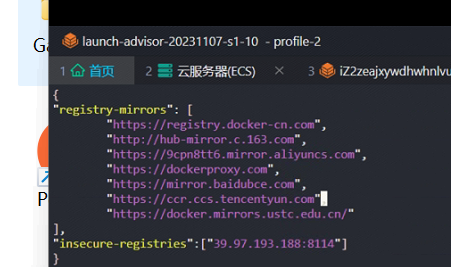
【大事件】docker可能无法使用了
今天本想继续学习docker的命令,突然发现官方网站的文档页面打不开了。 难道是被墙了? 我用同事的翻了一下,能进,果然! 正好手头的工作告一段落,将代码上传,然后通过jenkins将服务器自动部署到…...

探索Linux中的gzip命令:压缩与解压缩的艺术
探索Linux中的gzip命令:压缩与解压缩的艺术 在Linux世界中,文件压缩和解压缩是日常任务中不可或缺的一部分。gzip命令是这些任务中的佼佼者,它提供了高效的压缩和解压缩功能,广泛应用于各种场景。本文将带您深入了解gzip命令的工…...

Shell 输入/输出重定向
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 💝Ὁ…...

为什么RPC要比Http高效?
RPC和HTTP RPC(Remote Procedure Call)基于TCP连接通常比HTTP在性能上要高很多,原因如下: 1. 协议开销 HTTP开销: HTTP协议报文头部相对较大,包含大量的元数据(如方法、URI、头字段等&#x…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
