SpringCloud Consul基础入门与使用实践总结
【1】Consul简介
官网地址:https://www.consul.io/intro/index.html
下载地址:https://www.consul.io/downloads.html
中文文档:https://www.springcloud.cc/spring-cloud-consul.html
① 基础概念
Consul 是一套开源的分布式服务发现和配置管理系统,由 HashiCorp 公司用 Go 语言开发。
提供了微服务系统中的服务治理、配置中心、控制总线等功能。这些功能中的每一个都可以根据需要单独使用,也可以一起使用以构建全方位的服务网格,总之Consul提供了一种完整的服务网格解决方案。
它具有很多优点。包括:
- 基于 raft 协议,比较简洁;
- 支持健康检查,
- 同时支持 HTTP 和 DNS 协议
- 支持跨数据中心的 WAN 集群
- 提供图形界面
- 跨平台,支持 Linux、Mac、Windows
② 应用能力

- 服务发现 : 提供HTTP和DNS两种发现方式。
- 健康监测 : 支持多种方式,HTTP、TCP、Docker、Shell脚本定制化监控
- KV存储 : Key、Value的存储方式
- 多数据中心 : Consul支持多数据中心
- 可视化Web界面
③ windows下安装说明
官网安装说明:https://learn.hashicorp.com/consul/getting-started/install.html
下载地址:https://www.consul.io/downloads.html ,如下所示点击下载会得到一个exe安装文件。

傻瓜式安装后,我们以开发模式启动:
consul agent -dev
通过以下地址可以访问Consul的首页:http://localhost:8500
【2】应用实践
服务分为提供者和消费者,我们从两方面进行实践。
① 服务提供者
pom文件引入依赖:
<dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-consul-discovery</artifactId>
</dependency>
yml文件进行配置:
###consul服务端口号
server:port: 8006spring:application:name: consul-provider-payment
####consul注册中心地址cloud:consul:host: localhostport: 8500discovery:#hostname: 127.0.0.1service-name: ${spring.application.name}
主启动类添加注解:
@EnableDiscoveryClient
② 服务消费者
pom文件引入依赖:
<dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-consul-discovery</artifactId>
</dependency>
yml文件修改配置:
###consul服务端口号
server:port: 80spring:application:name: cloud-consumer-order
####consul注册中心地址cloud:consul:host: localhostport: 8500discovery:#hostname: 127.0.0.1service-name: ${spring.application.name}主启动类添加注解:
@EnableDiscoveryClient
可以看到,服务提供者和发现者关于Consul的配置是一样的。
【3】Eureka、Zookeeper与Consul三者异同
| 组件 | 语言 | CAP | 健康检查 | 对外接口 |
|---|---|---|---|---|
| Eureka | Java | AP | 可配支持 | HTTP |
| Consul | Go | CP | 支持 | HTTP/DNS |
| Zookeeper | Java | CP | 支持 | 客户端 |
① CAP
从CAP理论来进行分析。 众所周知,所有的中间件最多只能同时较好的满足两个。
CAP理论的核心是:一个分布式系统不可能同时很好的满足一致性,可用性和分区容错性这三个需求,
因此,根据 CAP 原理分成了满足 CA 原则、满足 CP 原则和满足 AP 原则三 大类:
- CA - 单点集群,满足一致性,可用性的系统,通常在可扩展性上不太强大。
- CP - 满足一致性,分区容忍必的系统,通常性能不是特别高。
- AP - 满足可用性,分区容忍性的系统,通常可能对一致性要求低一些。

② AP(Eureka)
当网络分区出现后,为了保证可用性,系统B可以返回旧值,保证系统的可用性。
结论:违背了一致性C的要求,只满足可用性和分区容错,即AP

③ CP(ZK/Consul)
当网络分区出现后,为了保证一致性,就必须拒接请求,否则无法保证一致性
结论:违背了可用性A的要求,只满足一致性和分区容错,即CP。

相关文章:

SpringCloud Consul基础入门与使用实践总结
【1】Consul简介 官网地址:https://www.consul.io/intro/index.html 下载地址:https://www.consul.io/downloads.html 中文文档:https://www.springcloud.cc/spring-cloud-consul.html ① 基础概念 Consul 是一套开源的分布式服务发现和…...
pdf拆分成有图和无图的pdf(方便打印)
pdf拆分成有图和无图的pdf(方便打印) 原因 打印图片要彩印,每次都要手动弄,打印的时候很麻烦; 随着打印次数的增加,时间就越来越多 为解决此问题,使用python写一个exe解决这个问题 历程 找一个python的GUI界面找到 t…...

通用树查找算法
想要一个树形控件来显示数据,却发现Racket的GUI库竟然没有提供这个控件。既然没有,那就自己手搓一个吧。没想到,在做这个控件中竟然有了新发现! 树形控件有一个功能是查找树中指定的节点。这就是接下来的故事的起点。 1 找外援 不…...

Flutter 中的 TableCell 小部件:全面指南
Flutter 中的 TableCell 小部件:全面指南 Flutter 是一个功能强大的 UI 框架,由 Google 开发,允许开发者使用 Dart 语言构建跨平台的移动、Web 和桌面应用。在 Flutter 的丰富组件库中,TableCell 是一个用于创建表格单元格的组件…...
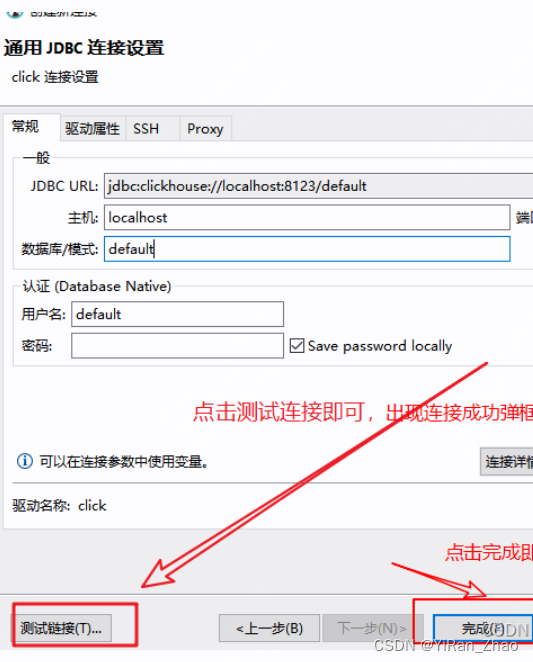
clickhouse学习笔记(一)入门与安装
目录 一 、入门 简介 核心特性包括 1.1 列式存储 1.2 原生压缩 1.3 向量化执行引擎 1.4 DBMS 功能 1.5 分布式处理 1.6 高吞吐写入能力 1.7 实时分析 1.8 SQL支持 1.9 高度可扩展 1.10 数据分区与线程级并行 1.11 应用场景 1.12 不适用场景 二、ClickHouse单机版…...

【JavaEE精炼宝库】多线程(4)深度理解死锁、内存可见性、volatile关键字、wait、notify
目录 一、死锁 1.1 出现死锁的常见场景: 1.2 产生死锁的后果: 1.3 如何避免死锁: 二、内存可见性 2.1 由内存可见性产生的经典案例: 2.2 volatile 关键字: 2.2.1 volatile 用法: 2.2.2 volatile 不…...
使用Ollama+OpenWebUI部署和使用Phi-3微软AI大模型完整指南
🏡作者主页: 点击! 🤖AI大模型部署与应用专栏:点击! ⏰️创作时间:2024年6月6日23点50分 🀄️文章质量:96分 欢迎来到Phi-3模型的奇妙世界!Phi-3是由微软…...

k8s的ci/cd实践之旅
书接上回k8s集群搭建完毕,来使用它强大的扩缩容能力帮我们进行应用的持续集成和持续部署,整体的机器规划如下: 1.192.168.8.156 搭建gitlab私服 docker pull gitlab/gitlab-ce:latest docker run --detach --hostname 192.168.8.156 --publ…...
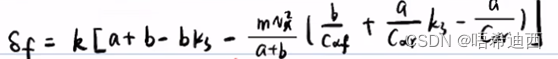
笔记96:前馈控制 + 航向误差
1. 回顾 对于一个 系统而言,结构可以画作: 如果采用 这样的控制策略,结构可以画作:(这就是LQR控制) 使用LQR控制器,可以通过公式 和 构建一个完美的负反馈系统; a a 但是有上…...

延时任务工具类
自定义工具类 package com.sxfoundation.task;import org.springframework.beans.factory.annotation.Autowired; import org.springframework.core.task.TaskRejectedException; import org.springframework.scheduling.concurrent.ThreadPoolTaskScheduler; import org.spri…...
springboot下载grpc编译文件,报错缺少protoc-gen-grpc-java:1.34.1:exe不存在
报错如图所示 [ERROR] Then, install it using the command: [ERROR] mvn install:install-file -DgroupIdio.grpc -DartifactIdprotoc-gen-grpc-java -Dversion1.34.1 -Dclassifierwindows-x86_64 -Dpackagingexe -Dfile/path/to/file [ERROR] [ERROR] Alternatively, if yo…...

【面试干货】 非关系型数据库(NoSQL)与 关系型数据库(RDBMS)的比较
【面试干货】 非关系型数据库(NoSQL)与 关系型数据库(RDBMS)的比较 一、引言二、非关系型数据库(NoSQL)2.1 优势 三、关系型数据库(RDBMS)3.1 优势 四、结论 💖The Begin…...

JAVA学习-练习试用Java实现“简化路径”
问题: 给定一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 / 开头),请将其转化为更加简洁的规范路径。 在 Unix 风格的文件系统中,一个点(.)表示当前目录本身…...
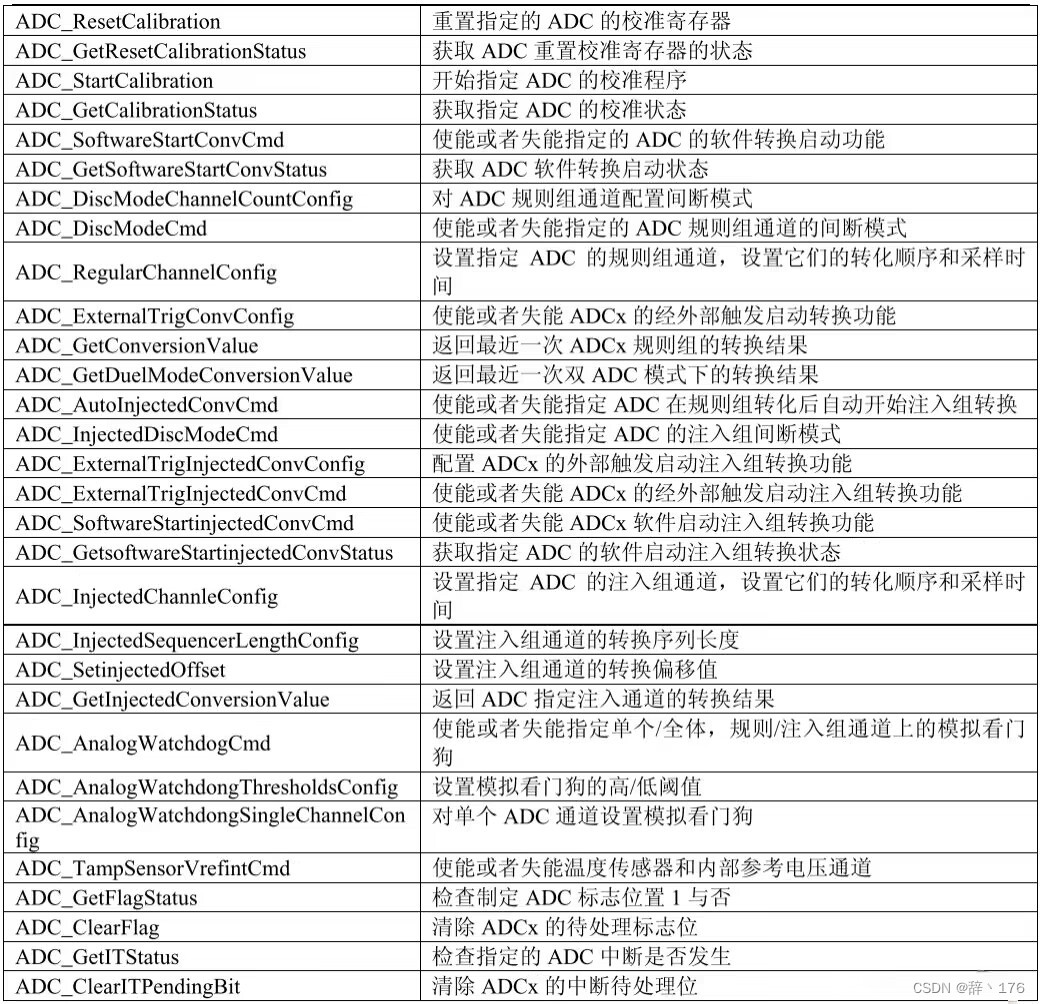
STM32——ADC篇(ADC的使用)
一、ADC的介绍 1.1什么是ADC ADC(Analogto-Digital Converter)模拟数字转换器,是将模拟信号转换成数字信号的一种外设。比如某一个电阻两端的是一个模拟信号,单片机无法直接采集,此时需要ADC先将短租两端的电…...

(文章复现)基于主从博弈的售电商多元零售套餐设计与多级市场购电策略
参考文献: [1]潘虹锦,高红均,杨艳红,等.基于主从博弈的售电商多元零售套餐设计与多级市场购电策略[J].中国电机工程学报,2022,42(13):4785-4800. 1.摘要 随着电力市场改革的发展,如何制定吸引用户选择的多类型零售套餐成为提升售电商利润的研究重点。为…...

深度评价GPT-4o:探索人工智能的新里程碑
在人工智能领域,OpenAI的GPT系列自推出以来就备受瞩目。GPT-4o作为该系列的最新版本,无疑是迄今为止最为强大的一代。它不仅在技术性能上有了质的飞跃,而且在应用的广泛性和深度上都展现出了惊人的潜力。本文将从版本对比、技术能力、使用体验…...

Linux命令篇(六):vi/vim专项
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝您生活愉快! 文章目录 一、什么是vim二…...

Java 还能不能继续搞了?
金三银四招聘季已落幕,虽说行情不是很乐观,但真正的强者从不抱怨。 在此期间,我收到众多小伙伴的宝贵反馈,整理出132道面试题,从基础到高级,有八股文,也有对某个知识点的深度解析。包括以下几部…...

【日记】遇到了一个很奇怪的大爷(845 字)
正文 花了昨天和今天两天时间,把数据转移完了。这块 2T 的硬盘可以光荣退休了。目前是没什么存储焦虑了。 农发行净开发一些垃圾系统。今天没什么业务,但跟 ActiveX 斗智斗勇了一整天,最后实在搞不过 IE 浏览器。我也懒得管了,又不…...
Python 机器学习 基础 之 处理文本数据 【处理文本数据/用字符串表示数据类型/将文本数据表示为词袋】的简单说明
Python 机器学习 基础 之 处理文本数据 【处理文本数据/用字符串表示数据类型/将文本数据表示为词袋】的简单说明 目录 Python 机器学习 基础 之 处理文本数据 【处理文本数据/用字符串表示数据类型/将文本数据表示为词袋】的简单说明 一、简单介绍 二、处理文本数据 三、用…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
