C++ AVL树 详细讲解
目录
一、AVL树的概念
二、AVL树的实现
1.AVL树节点的定义
2.AVL树的插入
3.AVL树的旋转
4.AVL树的验证
三、AVL树的性能
四、完结撒❀
一、AVL树的概念
● 它的左右子树都是 AVL 树● 左右子树高度之差 ( 简称平衡因子 ) 的绝对值不超过 1(-1/0/1)

二、AVL树的实现
1.AVL树节点的定义
AVL树节点的定义:
template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft; // 该节点的左孩子AVLTreeNode<T>* _pRight; // 该节点的右孩子AVLTreeNode<T>* _pParent; // 该节点的双亲T _data;int _bf; // 该节点的平衡因子
};2.AVL树的插入
1. 按照二叉搜索树的方式插入新节点2. 调整节点的平衡因子
bool Insert(const pair<K, V>& kv)
{// 1. 先按照二叉搜索树的规则将节点插入到AVL树中if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{//插入相同值return false;}}//找到cur所在位置cur = new Node(kv);if (parent->_kv.first > cur->_kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}// 2. 新节点插入后,AVL树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否//破坏了AVL树的平衡性/*pCur插入后,pParent的平衡因子一定需要调整,在插入之前,pParent的平衡因子分为三种情况:-1,0, 1, 分以下两种情况:1. 如果pCur插入到pParent的左侧,只需给pParent的平衡因子-1即可2. 如果pCur插入到pParent的右侧,只需给pParent的平衡因子+1即可此时:pParent的平衡因子可能有三种情况:0,正负1, 正负21. 如果pParent的平衡因子为0,说明插入之前pParent的平衡因子为正负1,插入后被调整成0,此时满足
AVL树的性质,插入成功2. 如果pParent的平衡因子为正负1,说明插入前pParent的平衡因子一定为0,插入后被更新成正负1,此
时以pParent为根的树的高度增加,需要继续向上更新3. 如果pParent的平衡因子为正负2,则pParent的平衡因子违反平衡树的性质,需要对其进行旋转处理*///更新平衡因子while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){//二叉树高度没问题,更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 插入前双亲的平衡因子是0,插入后双亲的平衡因子为1 或者 -1 ,说明以双亲为根的二叉树// 的高度增加了一层,因此需要继续向上调整cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){//双亲的平衡因子为正负2,违反了AVL树的平衡性//二叉树平衡被破坏,需要旋转完成平衡//判断是右单旋还是左单旋还是双旋//右单旋if (parent->_bf == -2 && cur->_bf == -1){//...}//左单旋else if (parent->_bf == 2 && cur->_bf == 1){//...}//左右双旋else if (parent->_bf == -2 && cur->_bf == 1){//...}//右左双旋else if (parent->_bf == 2 && cur->_bf == -1){//...}}else{//理论上不会出现这种状况assert(false);}}return true;
}3.AVL树的旋转

/*上图在插入前,AVL树是平衡的,新节点插入到30的左子树(注意:此处不是左孩子)中,30左
子树增加了一层,导致以60为根的二叉树不平衡,要让60平衡,只能将60左子树的高度减少一层,右子
树增加一层,即将左子树往上提,这样60转下来,因为60比30大,只能将其放在30的右子树,而如果30有
右子树,右子树根的值一定大于30,小于60,只能将其放在60的左子树,旋转完成后,更新节点
的平衡因子即可。在旋转过程中,有以下几种情况需要考虑:1. 30节点的右孩子可能存在,也可能不存在2. 60可能是根节点,也可能是子树如果是根节点,旋转完成后,要更新根节点如果是子树,可能是某个节点的左子树,也可能是右子树此处可举一些详细的例子进行画图,考虑各种情况,加深旋转的理解
*/
void _RotateR(Node Parent)
{// SubL: Parent的左孩子// SubLR: Parent左孩子的右孩子,注意:该Node SubL = Parent->_Left;Node SubLR = SubL->_Right;// 旋转完成之后,30的右孩子作为双亲的左孩子Parent->_Left = SubLR;// 如果30的左孩子的右孩子存在,更新亲双亲if (SubLR)SubLR->_Parent = Parent;// 60 作为 30的右孩子SubL->_Right = Parent;// 因为60可能是棵子树,因此在更新其双亲前必须先保存60的双亲Node Parent = Parent->_Parent;// 更新60的双亲Parent->_Parent = SubL;// 更新30的双亲SubL->_Parent = Parent;// 如果60是根节点,根新指向根节点的指针if (NULL == Parent){_root = SubL;SubL->_Parent = NULL;}else{// 如果60是子树,可能是其双亲的左子树,也可能是右子树if (Parent->_Left == Parent)Parent->_Left = SubL;elseParent->_Right = SubL;}// 根据调整后的结构更新部分节点的平衡因子Parent->_bf = SubL->_bf = 0;
}2) 新节点插入较高右子树的右侧---右右:左单旋
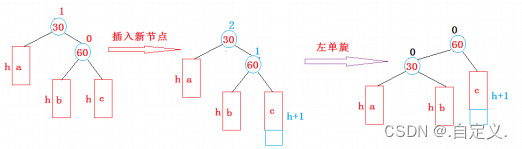
//左单旋
void LNode(Node* parent)
{/*if (parent == _root){Node* pparent = nullptr;}else{Node* pparent = parent->_parent;}*/Node* pparent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_left = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (pparent){subR->_parent = pparent;if (pparent->_left = parent){pparent->_left = subR;}else{pparent->_right = subR;}}else{_root = subR;subR->_parent = nullptr;}parent->_bf = subR->_bf = 0;
}3) 新节点插入较高左子树的右侧---左右:先左单旋再右单旋

// 旋转之前,60的平衡因子可能是-1/0/1,旋转完成之后,根据情况对其他节点的平衡因子进
//行调整
void _RotateLR(Node Parent)
{Node SubL = Parent->_Left;Node SubLR = SubL->_Right;// 旋转之前,保存pSubLR的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节点的平衡因子int bf = SubLR->_bf;// 先对30进行左单旋_RotateL(Parent->_Left);// 再对90进行右单旋_RotateR(Parent);if (1 == bf)SubL->_bf = -1;else if (-1 == bf)Parent->_bf = 1;
}4) 新节点插入较高右子树的左侧---右左:先右单旋再左单旋

//右左双旋
void RLNode(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RNode(parent->_right);LNode(parent);if (bf == 1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;parent->_bf = 0;}else if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else{//理论没有该状况assert(false);}
}当 SubR 的平衡因子为 1 时,执行左单旋当 SubR 的平衡因子为 -1 时,执行右左双旋
当 SubL 的平衡因子为 -1 是,执行右单旋当 SubL 的平衡因子为 1 时,执行左右双旋
4.AVL树的验证
int _size(Node* root)
{return root == nullptr ? 0 : _size(root->_left) + _size(root->_right) + 1;
}int _Height(Node* root)
{if (root == nullptr){return 0;}return max(_Height(root->_left), _Height(root->_right)) + 1;
}bool _IsBalance(Node* root)
{if (root == nullptr){return true;}int LeftHeight = _Height(root->_left);int RightHeight = _Height(root->_right);if (abs(LeftHeight - RightHeight) >= 2){return false;}//可以顺便再检查一下平衡因子if (abs(LeftHeight - RightHeight) != root->_bf){cout << root->_kv.first << endl;return false;}return _IsBalance(root->_left) && _IsBalance(root->_right);
}三、AVL树的性能
四、完结撒❀
如果以上内容对你有帮助不妨点赞支持一下,以后还会分享更多编程知识,我们一起进步。
最后我想讲的是,据说点赞的都能找到漂亮女朋友❤

相关文章:

C++ AVL树 详细讲解
目录 一、AVL树的概念 二、AVL树的实现 1.AVL树节点的定义 2.AVL树的插入 3.AVL树的旋转 4.AVL树的验证 三、AVL树的性能 四、完结撒❀ 一、AVL树的概念 二叉搜索树虽可以缩短查找的效率,但 如果数据有序或接近有序二叉搜索树将退化为单支树,查 …...

Faster R-CNN:端到端的目标检测网络
本文回顾了由微软研究人员开发的 Faster R-CNN 模型。Faster R-CNN 是一种用于物体检测的深度卷积网络,在用户看来,它是一个单一的、端到端的统一网络。该网络可以准确快速地预测不同物体的位置。为了真正理解 Faster R-CNN,我们还必须快速概…...

如何给 MySQL 表和列授予权限?(官方版)
目录 授予表级别权限 授予列级别权限 如何给MySQL表和列授予权限是MySQL数据操作中非常重要的步骤,也是企业级使用MySQL数据库的起步点,以下分别参照官方教程整理的MySQL数据库的权限操作。 以下的语句可以直接使用MySQL的命令行进行操作(如何…...
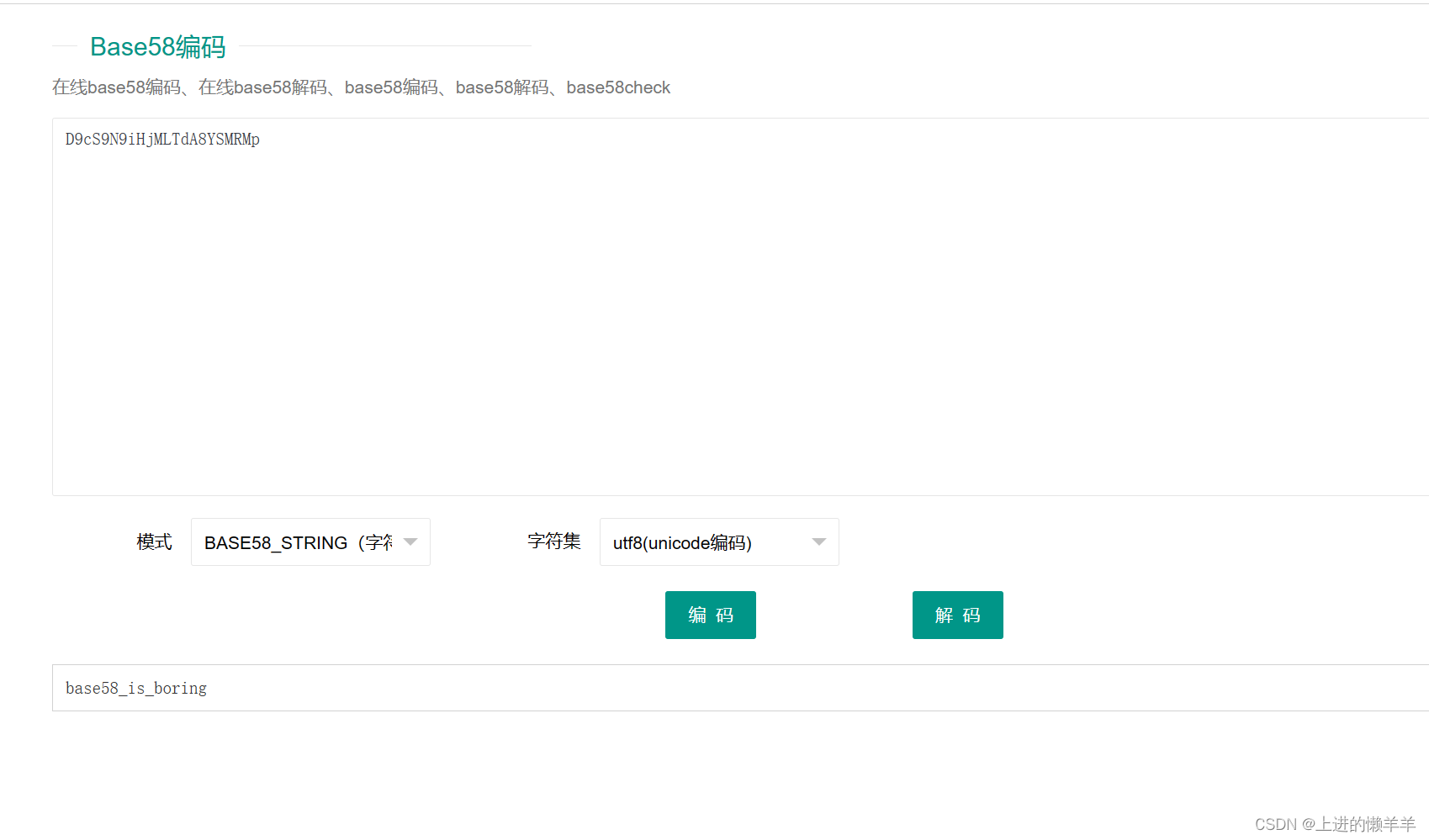
攻防世界testre做法(考点:base58)
在做这道题目之前,我们先来简单了解一下base64加密和base58加密,先来说一些预备知识,bit为1个位,即一个0或1,八个位组成一个字节,即八个二进制数。 base64编码原理:1,在使用base64加…...
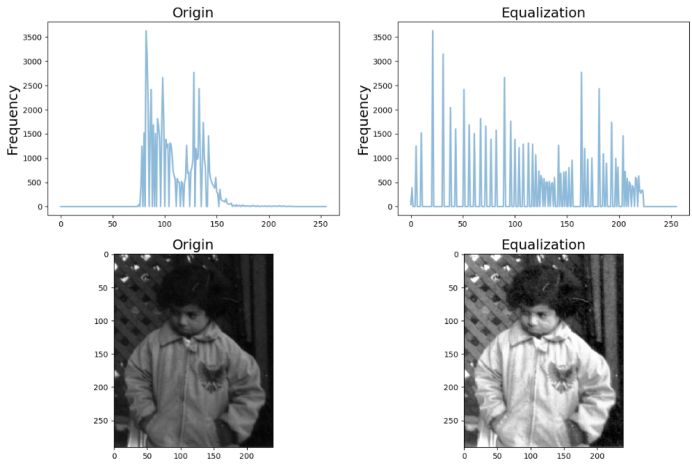
计算机视觉与模式识别实验1-1 图像的直方图平衡
文章目录 🧡🧡实验流程🧡🧡1.读入图像‘rice.png’,在一个窗口中显示灰度级n64,128和256的图像直方图。2.调解图像灰度范围,观察变换后的图像及其直方图的变化。3.分别对图像‘pout.tif’和‘ti…...
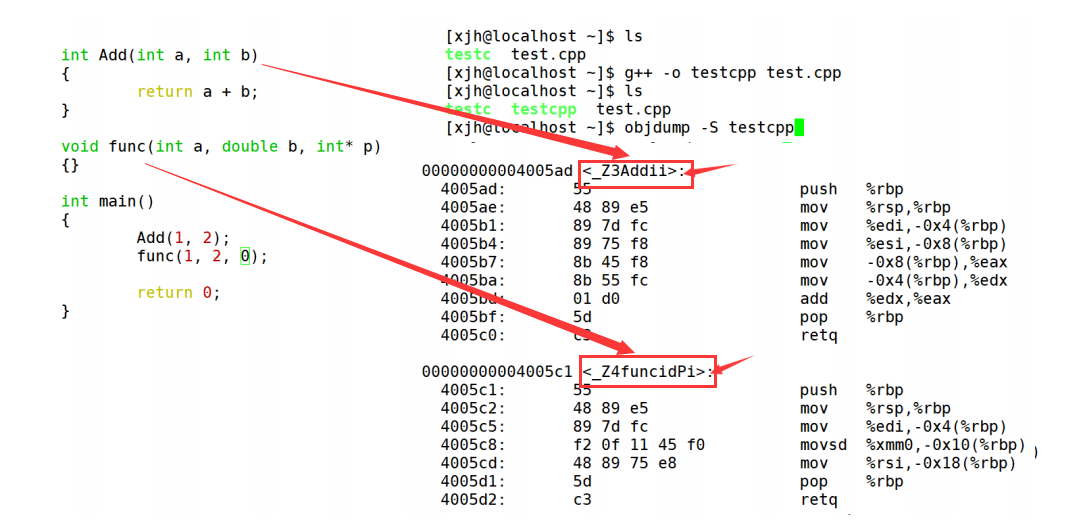
【C++课程学习】:C++入门(函数重载)
🎁个人主页:我们的五年 🔍系列专栏:C课程学习 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 🌈函数重载: 🍉1.参数个数不同: 🍉2.参数…...
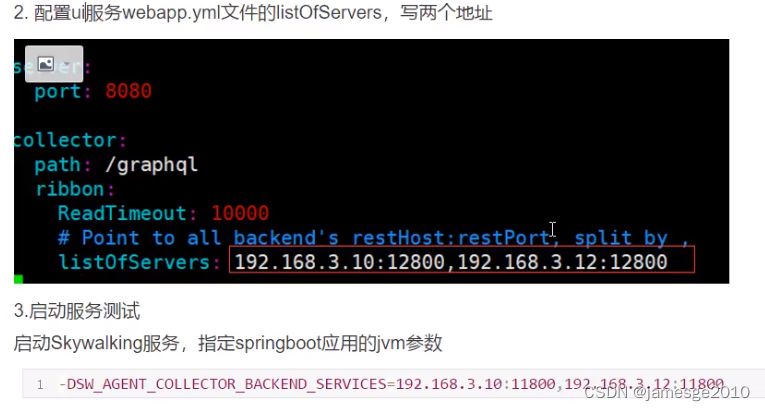
skywalking介绍及搭建
链路追踪框架比对: skywalking安装部署: 下载地址:Downloads | Apache SkyWalking 配置微服务与skywalking整合: copy agent/optional-plugins/apm-spring-cloud-getway-xx.jar到plugins,然后重启skywalking 监控界面…...
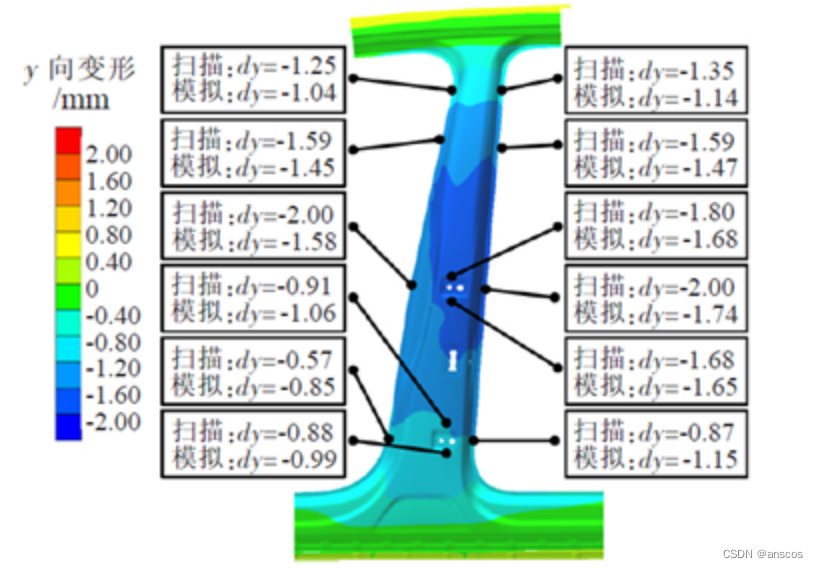
分析示例 | Simufact焊接工艺仿真变形精确预测汽车结构
导语 焊接是汽车制造过程中一个关键环节,白车身、发动机、底盘和变速箱等都离不开焊接工艺的应用,主要涉及气保焊、电阻点焊、激光焊、电子束焊等多种焊接工艺。由于汽车车型众多、成形结构复杂、汽车制造质量、效率、成本等方面的综合要求。如何高效、…...

模式识别选择题
影响K-均值聚类算法效果的主要因素之一是什么? A. 初始聚类中心的选取 B. 样本输入顺序 C. 模式相似性测度 D. 分类准则 答案:A支持向量机(SVM)在处理非线性问题时,通常使用什么方法? A. 引入核函数 B. 增加…...

【Java基础】线程方法
start():启动线程,使线程进入就绪状态。 run():线程执行的代码逻辑,需要重写该方法。 停止线程 void interrupt() 中断线程,让它重新去争抢cpu 如果目标线程长时间等待,则应该使用interrupt方法来中断等待…...

C++之动态数组
C给我们提供了一个叫Vector的类,这个Vector在std命名空间中。这个Vector有点像一个集合,一个不强制其实际元素具有唯一性的集合,和数组一样,但是和C普通的数组又不太一样,和标准的数组不同当你创建Vector时,…...

使用 image-combiner 开源项目实现对海报图片的生成
1:gitee 项目地址 image-combiner: ImageCombiner是一个专门用于Java服务端图片合成的工具,没有很复杂的功能,简单实用,从实际业务场景出发,提供简单的接口,几行代码即可实现图片拼合(当然用于…...

【缓存】框架层常见问题和对策
缓存是为了加快读写速度,再了解redis这类框架层的缓存应用之前,我们不妨先思考下操作系统层面的缓存解决方案,这样有助于我们更深的理解缓存,哪些是系统层面的,哪些是服务层面。 以下是一些常见的缓存问题及其解决方案…...

【FAS】《CN103106397B》
原文 CN103106397B-基于亮瞳效应的人脸活体检测方法-授权-2013.01.19 华南理工大学 方法 / 点评 核心方法用的是传统的形态学和模板匹配,亮点是双红外发射器做差分 差分:所述FPGA芯片控制两组红外光源(一近一远)交替亮灭&…...

3D按F3为什么显示不出模型?---模大狮模型网
对于3D建模软件的用户来说,按下F3键通常是用来显示或隐藏模型的功能之一。然而,有时当按下F3键时,却无法正确显示模型,这可能会让用户感到困惑。模大狮将探讨这种情况发生的可能原因以及解决方法,帮助设计师们更好地理…...
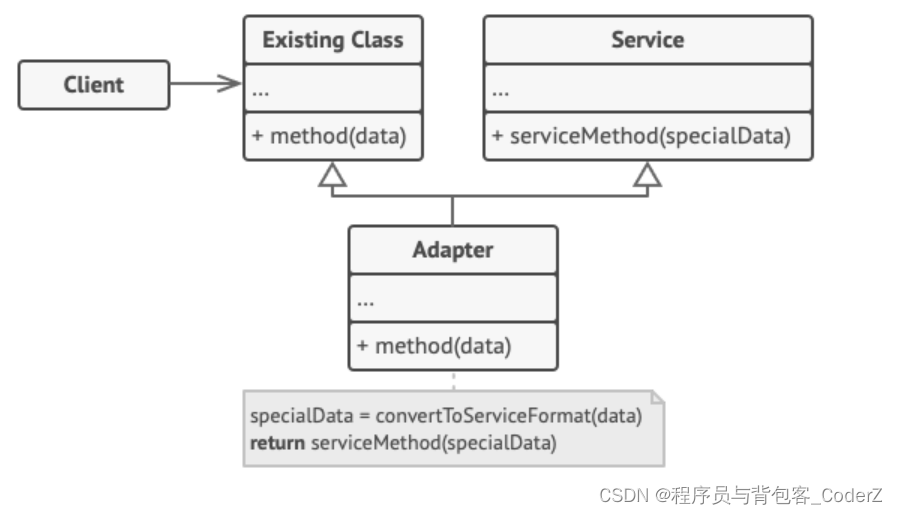
C++设计模式——Adapter适配器模式
一,适配器模式简介 适配器模式是一种结构型设计模式,用于将已有接口转换为调用者所期望的另一种接口。 适配器模式让特定的API接口可以适配多种场景。例如,现有一个名为"Reader()"的API接口只能解析txt格式的文件,给这…...

Python文本处理利器:jieba库全解析
文章目录 Python文本处理利器:jieba库全解析第一部分:背景和功能介绍第二部分:库的概述第三部分:安装方法第四部分:常用库函数介绍1. 精确模式分词2. 全模式分词3. 搜索引擎模式分词4. 添加自定义词典5. 关键词提取 第…...

【C/C++】C语言如何实现类似C++的智能指针?
在C中,智能指针是为了自动化资源管理而引入的工具。比如std::unique_ptr和std::shared_ptr等,它们管理着所持有对象的生命周期,可以在智能指针被销毁时自动释放其所持有的资源。在C语言中,虽然没有直接的智能指针概念,…...
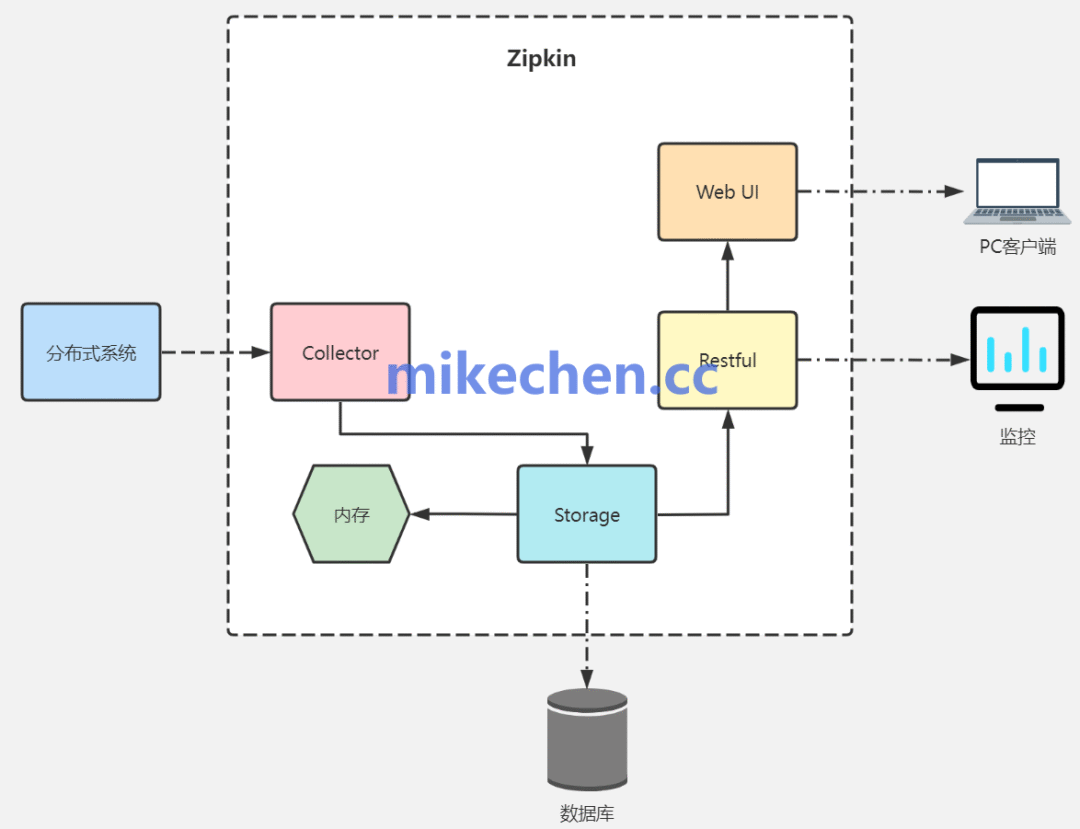
九大微服务监控工具详解
Prometheus Prometheus 是一个开源的系统监控、和报警工具包,Prometheus 被设计用来监控“微服务架构”。 主要解决: 监控和告警:Prometheus 可以对系统、和应用程序进行实时监控,并在出现问题时发送告警;数据收集和…...

java aliyun oss上传和下载工具类
java aliyun oss上传和下载工具类 依赖 <dependency><groupId>com.aliyun.oss</groupId><artifactId>aliyun-sdk-oss</artifactId><version>3.8.0</version></dependency>工具类 import com.alibaba.fastjson.JSON; import c…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
