数据结构:线索二叉树
目录
1.线索二叉树是什么?
2.包含头文件
3.结点设计
4.接口函数定义
5.接口函数实现
线索二叉树是什么?
线索二叉树(Threaded Binary Tree)是一种对普通二叉树的扩展,它通过在树的某些空指针上添加线索来实现更高效的遍历操作。线索二叉树的目的是减少查找特定节点(如前驱或后继节点)所需的时间,从而提高树的搜索效率。以下是线索二叉树的特点:
1.普通二叉树的扩展:线索二叉树是基于普通二叉树的,它保留了二叉树的所有性质。
2.线索:在二叉树的空指针(左子树或右子树的指针)上添加线索,这些线索可以指导我们找到节点的前驱或后继。
3.前驱和后继:每个节点的前驱是其在中序遍历中直接前的一个节点,后继是直接后的节点。线索二叉树允许我们通过线索快速找到这些节点。
包含头文件
#include<stdio.h>
#include<stdlib.h>结点设计
#define Initsize 100
typedef char Elemtype;typedef struct ThreadTree {Elemtype data; //定义Elemtype类型的变量存储结点值struct ThreadTree* lchild; //定义ThreadTree类型的指针变量lchild存储左子树的地址struct ThreadTree* rchild; //定义ThreadTree类型的指针变量rchild存储右子树的地址int Lvalue, Rvalue; //定义int类型的变量Lvalue和Rvalue分别标识线索
}ThreadTree,* ThTree;ThTree Pre = NULL; //定义ThTree类型的全局变量Pre指向此次结点的前驱结点接口函数定义
void InitThTree(ThTree& A); //用于初始化线索二叉树
void InsertTree(ThTree& A); //用于输入数据建立二叉树
void InOrder(ThTree A); //用于在二叉树中执行中序遍历
void InOrderVisit(ThTree& A); //用于在结点中进行中序线索化
void InOrderThread(ThTree& A); //用于中序遍历线索化二叉树
void PreOrder(ThTree A); //用于在二叉树中执行先序遍历
void PreOrderVisit(ThTree& A); //用于先序遍历线索化二叉树
void PreOrderThread(ThTree& A); //用于先序遍历线索化二叉树
void PostOrder(ThTree A); //用于执行后序遍历
void PostOrderVisit(ThTree& A); //用于后序遍历线索化二叉树
void PostOrderThread(ThTree& A); //用于后序遍历线索化二叉树接口函数实现
void PostOrderThread(ThTree& A) { //用于后序遍历线索化二叉树Pre = NULL;if (A != NULL) {PostOrder(A);if (A->rchild == NULL){Pre->Rvalue = 1;}}
} void PostOrderVisit(ThTree& A) { //用于后序遍历线索化二叉树if (A->lchild == NULL) { //若传入的结点的左子树为空,则将该结点的左子树线索化A->Lvalue = 1;A->lchild = Pre;}if (A->rchild == NULL && Pre != NULL) {//若传入的结点的空子树为空,且前驱结点不为空,则将该结点的左子树线索化Pre->rchild = A;Pre->Rvalue = 1;}Pre = A;
} void PostOrder(ThTree A) { //用于执行后序遍历if (A != NULL) {PostOrder(A->lchild);PostOrder(A->rchild);PostOrderVisit(A);}
}void PreOrderThread(ThTree& A) { //用于先序遍历线索化二叉树Pre = NULL; if (A != NULL) {PreOrder(A);if (Pre->rchild == NULL) {Pre->Rvalue = 1;}}
}void PreOrderVisit(ThTree& A) { //用于先序遍历线索化二叉树if (A->lchild == NULL) { //若传入的结点的左子树为空,则将该结点的左子树线索化A->Lvalue = 1;A->lchild = Pre;}if (A->rchild == NULL && Pre != NULL) {//若传入的结点的空子树为空,且前驱结点不为空,则将该结点的左子树线索化Pre->Rvalue = 1;Pre->rchild = A;}Pre = A;
}void PreOrder(ThTree A) { //用于在二叉树中执行先序遍历if (A != NULL) {PreOrderVisit(A);if (A->Lvalue==0) {PreOrder(A->lchild);}PreOrder(A->rchild);}
}void InOrderThread(ThTree& A) { //用于中序遍历线索化二叉树Pre = NULL; //遍历第一个结点时,第一个结点无前驱结点,故Pre为NULLif (A != NULL) {InOrder(A); //进行中序遍历if (Pre->rchild == NULL) { //将中序遍历的最后一个结点的右子树线索化Pre->Rvalue = 1; //因为其结点无后继,故不更新指向}}
}void InOrderVisit(ThTree& A) { //用于在结点中进行线索化if (A->lchild == NULL) { //左子树若为空,则将其左子树线索化A->Lvalue = 1;A->lchild = Pre;}if (A->rchild == NULL && Pre != NULL) {//右子树若为空,则将其右子树线索化Pre->rchild = A;Pre->Rvalue = 1;}Pre = A; //更新指向前驱结点的指针pre
}void InOrder(ThTree A) { //用于在二叉树执行中序遍历if (A!= NULL) { InOrder(A->lchild);InOrderVisit(A);InOrder(A->rchild);}
}void InsertTree(ThTree& A) { //用于输入数据建立二叉树ThTree Q[Initsize], //定义ThTree类型的指针数组存储根结点的地址W = NULL; //定义Thtree类型的指针W指向新建的结点的地址int i=0, //定义int类型的变量i作为左右孩子树的标识j=0, //定义int类型的变量j作为字符串遍历的指针top=-1; //定义int类型的变量top作为结点数组的指针char E,R[Initsize];printf("请以括号法输入数据,并以此建立二叉树:");scanf_s("%s", R, Initsize);E = R[i];while (E != '\0') {switch (E) {case '(':top++; //入栈操作Q[top] = W;i = 1; //对新结点做标识,1为左子树的标识break;case ',':i = 2; //对新结点做标识,2为右子树的标识break;case ')':top--; //出栈操作break;default:W = (ThreadTree*)malloc(sizeof(ThreadTree)); //新建结点W->data = E; //更新结点的数据域data的指向W->rchild = W->lchild = NULL;if (A == NULL) { //当传入的结点为空时,则新建的结点为树的根结点A = W;}else {switch (i) { //判断传入的结点为左子树还是右子树case 1:Q[top]->lchild = W; //将栈内的根结点的lchild指向新建的地址break;case 2:Q[top]->rchild = W; //将栈内的根结点的rchild指向新建的地址break;}}}j++;E = R[j];}printf("构建线索二叉树对应的二叉树成功\n");
}void InitThTree(ThTree& A) { //用于初始化线索二叉树A = NULL;printf("初始化线索二叉树成功\n");
}相关文章:

数据结构:线索二叉树
目录 1.线索二叉树是什么? 2.包含头文件 3.结点设计 4.接口函数定义 5.接口函数实现 线索二叉树是什么? 线索二叉树(Threaded Binary Tree)是一种对普通二叉树的扩展,它通过在树的某些空指针上添加线索来实现更高效的遍…...
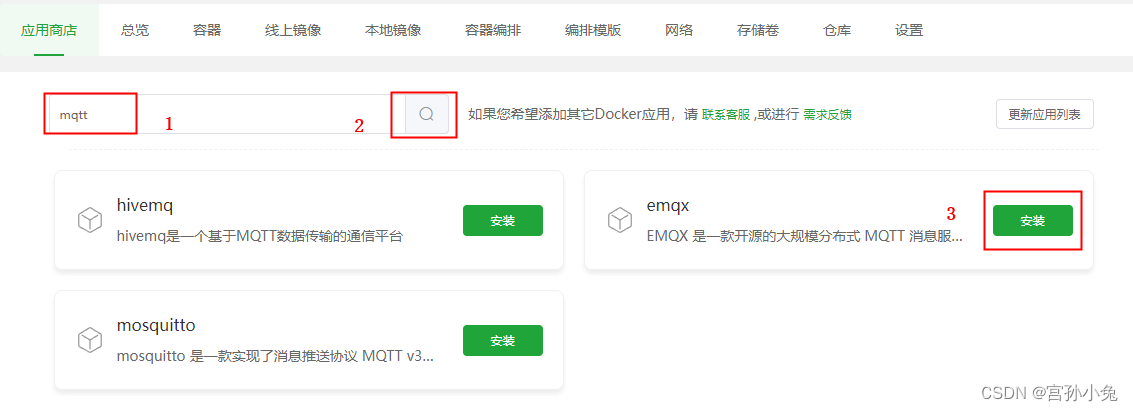
宝塔Linux面板-Docker管理(2024详解)
上一篇文章《宝塔Linux可视化运维面板-详细教程2024》,详细介绍了宝塔Linux面板的详细安装和配置方法。本文详细介绍使用Linux面板管理服务器Docker环境。 目录 1、安装Docker 1.1 在线安装 编辑 1.2 手动安装 1.3 运行状态 1.4 镜像加速 2 应用商店 3 总览 4 容器 …...

【Linux】进程(8):Linux真正是如何调度的
大家好,我是苏貝,本篇博客带大家了解Linux进程(8):Linux真正是如何调度的,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 之前我们讲过,在大…...

R语言探索与分析14-美国房价及其影响因素分析
一、选题背景 以多元线性回归统计模型为基础,用R语言对美国部分地区房价数据进行建模预测,进而探究提高多元回 归线性模型精度的方法。先对数据进行探索性预处理,随后设置虚拟变量并建模得出预测结果,再使用方差膨胀因子对 多重共…...

golang websocket 数据处理和返回JSON数据示例
golang中websocket数据处理和返回json数据示例, 直接上代码: // author tekintiangmail.com // golang websocket 数据处理和返回JSON数据示例, // 这个函数返回 http.HandlerFunc // 将http请求升级为websocket请求 这个需要依赖第三方包 …...

【Mac】Downie 4 for Mac(视频download工具)兼容14系统软件介绍及安装教程
前言 Downie 每周都会更新一个版本适配视频网站,如果遇到视频download不了的情况,请搜索最新版本https://mac.shuiche.cc/search/downie。 注意:Downie Mac特别版不能升级,在设置中找到更新一列,把自动更新和自动downl…...
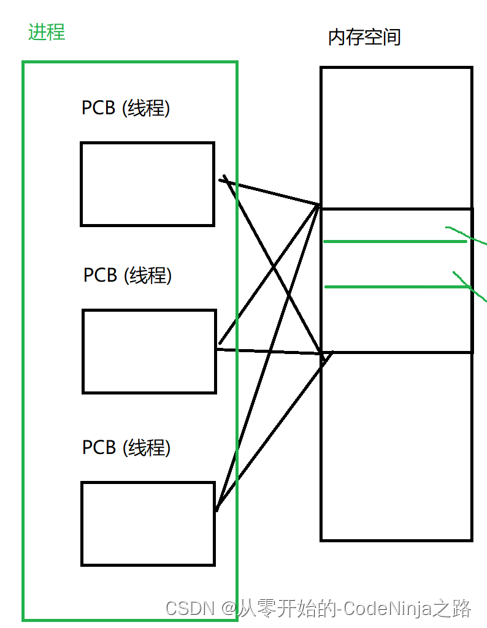
【操作系统】进程与线程的区别及总结(非常非常重要,面试必考题,其它文章可以不看,但这篇文章最后的总结你必须要看,满满的全是干货......)
目录 一、 进程1.1 PID(进程标识符)1.2 内存指针1.3 文件描述符表1.4 状态1.5 优先级1.6 记账信息1.7 上下文 二、线程三、总结:进程和线程之间的区别(非常非常非常重要,面试必考题) 一、 进程 简单来介绍一下什么是进程…...

自动驾驶仿真(高速道路)LaneKeeping
前言 A high-level decision agent trained by deep reinforcement learning (DRL) performs quantitative interpretation of behavioral planning performed in an autonomous driving (AD) highway simulation. The framework relies on the calculation of SHAP values an…...

数据挖掘实战-基于Catboost算法的艾滋病数据可视化与建模分析
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

分水岭算法分割和霍夫变换识别图像中的硬币
首先解释一下第一种分水岭算法: 一、分水岭算法 分水岭算法是一种基于拓扑学的图像分割技术,广泛应用于图像处理和计算机视觉领域。它将图像视为一个拓扑表面,其中亮度值代表高度。算法的目标是通过模拟雨水从山顶流到山谷的过程࿰…...

什么是AVIEXP提前发货通知?
EDI(电子数据交换)报文是一种用于电子商务和供应链管理的标准化信息传输格式。AVIEXP 是一种特定类型的 EDI 报文,用于传输提前发货通知信息。 AVIEXP 报文简介 AVIEXP 是指 Advanced Shipping Notification提前发货通知报文,用…...
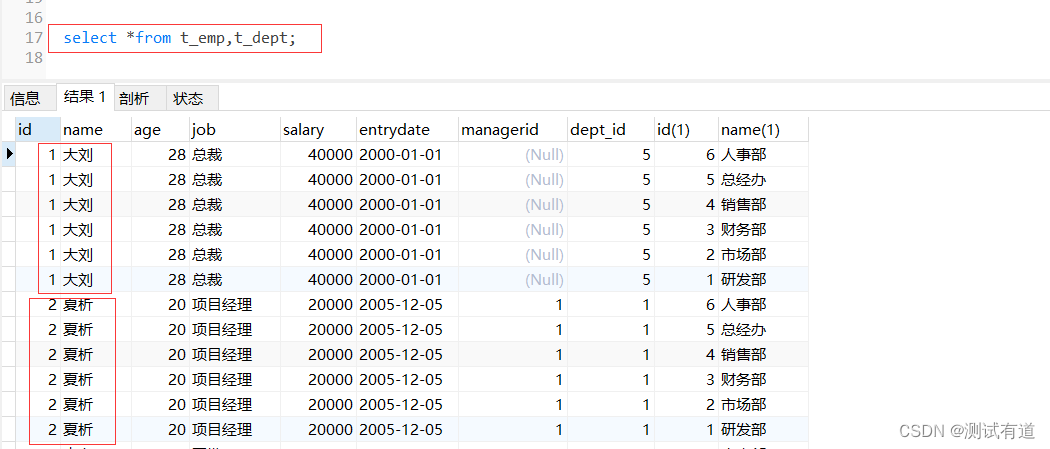
Python 之SQLAlchemy使用详细说明
目录 1、SQLAlchemy 1.1、ORM概述 1.2、SQLAlchemy概述 1.3、SQLAlchemy的组成部分 1.4、SQLAlchemy的使用 1.4.1、安装 1.4.2、创建数据库连接 1.4.3、执行原生SQL语句 1.4.4、映射已存在的表 1.4.5、创建表 1.4.5.1、创建表的两种方式 1、使用 Table 类直接创建表…...
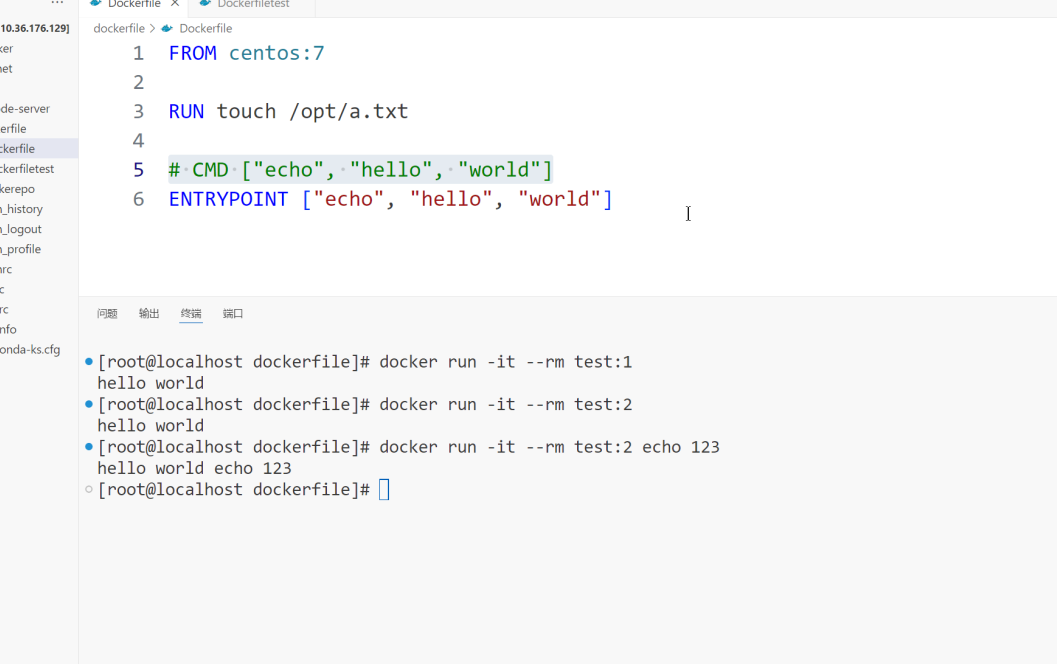
就业班 第四阶段(docker) 2401--5.29 day3 Dockerfile+前后段项目若依ruoyi
通过Dockerfile创建镜像 Docker 提供了一种更便捷的方式,叫作 Dockerfile docker build命令用于根据给定的Dockerfile构建Docker镜像。docker build语法: # docker build [OPTIONS] <PATH | URL | ->1. 常用选项说明 --build-arg,设…...

【运维项目经历|026】Redis智能集群构建与性能优化工程
🍁博主简介: 🏅云计算领域优质创作者 🏅2022年CSDN新星计划python赛道第一名 🏅2022年CSDN原力计划优质作者 🏅阿里云ACE认证高级工程师 🏅阿里云开发者社区专家博主 💊交流社区:CSDN云计算交流社区欢迎您的加入! 目…...

Linux编程for、while循环if判断以及case语句用法
简介 语法描述if条件语句if else条件判断语句if else-if else多条件判断语句for循环执行命令while循环执行命令until直到条件为真时停止循环case ... esac多选择语句break跳出循环continue跳出当前循环 1. for 循环 for语句,定量循环,可以遍历一个列表…...

docker命令 docker ps -l (latest)命令在 Docker 中用于列出最近一次创建的容器
文章目录 12345 1 docker ps -l 命令在 Docker 中用于列出最近一次创建的容器。具体来说: docker ps:这个命令用于列出当前正在运行的容器。-l 或 --latest:这个选项告诉 docker ps 命令只显示最近一次创建的容器,不论该容器当前…...

inflight 守恒和带宽资源守恒的有效性
接着昨天的问题,inflight 守恒的模型一定存在稳定点吗?并不是。如果相互抑制强度大于自我抑制强度,系统也会跑飞: 模拟结果如下: 所以一定要记得 a < b。 比对前两个图和后两个图的 a,b 参数关系&am…...
短视频直播教学课程小程序的作用是什么
只要短视频/直播做的好,营收通常都不在话下,近些年,线上自媒体行业热度非常高,每条细分赛道都有着博主/账号,其各种优势条件下也吸引着其他普通人冲入。 然无论老玩家还是新玩家,面对平台不断变化的规则和…...

Open AI又出王炸GPT-4,目测一大波人的饭碗要碎了...
前言 在科技的惊涛骇浪中,每一次技术的飞跃都预示着新时代的曙光。近日,Open AI公司再次震撼业界,推出了其最新力作——GPT-4,这款被誉为“王炸”的语言模型,以其前所未有的智能水平和创造力,不仅在技术圈…...
:转移指令的原理)
8086 汇编笔记(八):转移指令的原理
一、操作符 offset 操作符offset在汇编语言中是由编译器处理的符号,它的功能是取得标号的偏移地址 codesg segmentstart: mov ax,offset start ;相当于 mv ax,0s: mov ax,offset s ;相当于 mv ax,3codesg endsend start 二、jmp 指令 jmp为无条件…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
