如何设置vue3项目中默认的背景为白色
方法1:通过CSS全局样式
-
在全局CSS文件中设置:
如果你的项目中有全局的CSS文件(如App.vue或专门的CSS文件),你可以直接设置body或html标签的背景颜色。在
src/assets文件夹中(或者任何你存放CSS文件的地方),打开或创建一个CSS文件,例如global.css,然后添加以下样式:body, html {background-color: white; } -
在
main.js或main.ts中引入这个CSS文件:
确保在项目的入口文件(通常是main.js或main.ts)中导入你的全局CSS文件。import './assets/global.css';
方法2:在Vue组件中设置
如果你想在特定的Vue组件中设置背景色,可以直接在该组件的<style>标签中设置:
<template><div class="app-container"><!-- 组件内容 --></div>
</template><script>
export default {name: 'App'
}
</script><style>
.app-container {background-color: white; /* 设置白色背景 */min-height: 100vh; /* 确保背景覆盖整个视口高度 */
}
</style>
这种方法的好处是可以针对不同的组件设置不同的背景色。

相关文章:

如何设置vue3项目中默认的背景为白色
方法1:通过CSS全局样式 在全局CSS文件中设置: 如果你的项目中有全局的CSS文件(如App.vue或专门的CSS文件),你可以直接设置body或html标签的背景颜色。 在src/assets文件夹中(或者任何你存放CSS文件的地方&a…...

MS1112驱动开发
作者简介: 一个平凡而乐于分享的小比特,中南民族大学通信工程专业研究生在读,研究方向无线联邦学习 擅长领域:驱动开发,嵌入式软件开发,BSP开发 作者主页:一个平凡而乐于分享的小比特的个人主页…...
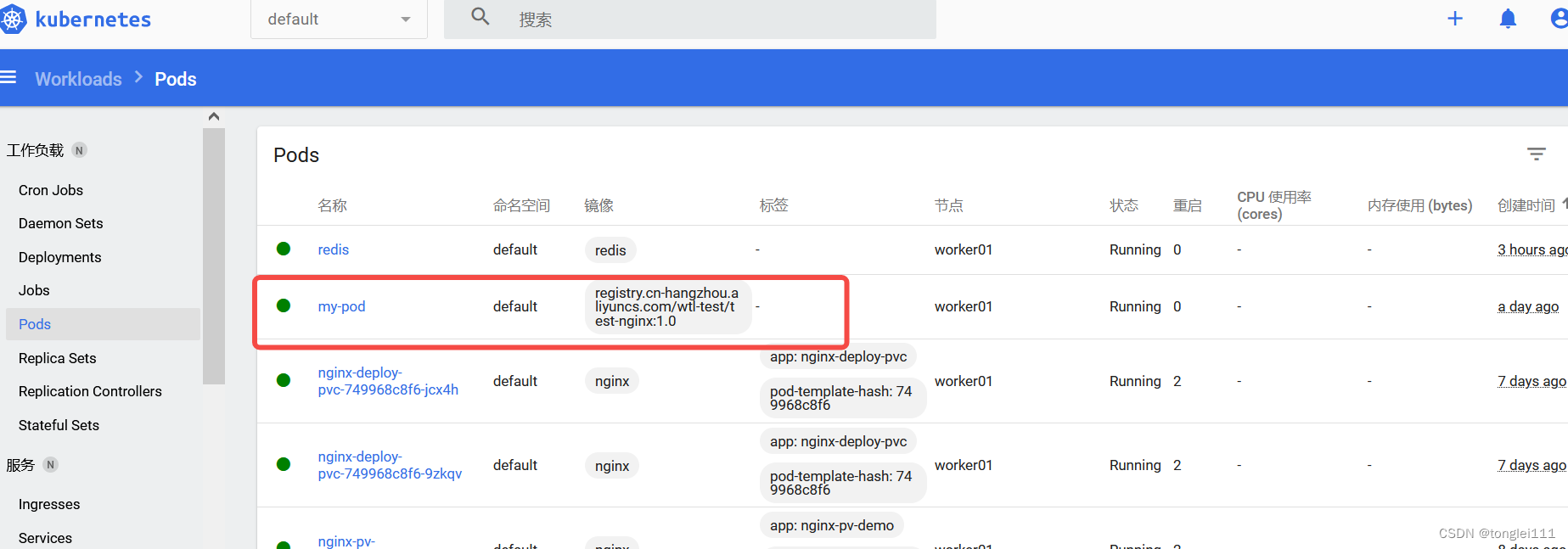
K8s存储对象的使用
背景和概念 容器中的文件在磁盘上是临时存放的,这给在容器中运行较重要的应用带来一些问题: 当容器崩溃或停止时,此时容器状态未保存, 因此在容器生命周期内创建或修改的所有文件都将丢失。另外 在崩溃期间,kubelet 会…...
构建自动化API数据抓取系统
构建一个自动化API数据抓取系统是一个涉及多个技术领域的复杂任务。这样的系统不仅要求高效的数据获取能力,还需要有稳定的数据处理、存储和错误处理机制。 1. 需求分析 在开始构建之前,明确你的需求至关重要。你需要确定要抓取的API、数据的频率、数据的…...
【Qt知识】部分QWidget属性表格
QWidget是Qt库中所有图形用户界面组件的基类,它提供了大量属性以供自定义和配置控件的行为和外观。下面列出了一些主要的QWidget属性及其作用。 属性 作用 accessibleName 控件的辅助技术名称,用于无障碍访问。 accessibleDescription 控件的辅助技…...

【ARM64 常见汇编指令学习 19.1 -- ARM64 跳转指令 b.pl 详细介绍】
文章目录 ARM64 跳转指令 b.pl使用场景语法示例总结 ARM64 跳转指令 b.pl 在 ARMv8 架构中,b.pl 是一条条件分支(Branch)指令,它根据当前的状态寄存器中的条件标志执行跳转。b.pl 的全称是 Branch if Plus,即如果条件…...

WWDC24即将到来,ios18放大招
苹果公司即将在下周开全球开发者大会(WWDC),大会上将展示其人工智能技术整合到设备和软件中的重大进展,包括与OpenAI的历史性合作。随着大会的临近,有关iOS 18及其据称采用AI技术支持的应用程序和功能的各种泄露信息已经浮出水面。 据报道,苹果将利用其自主研发的大…...

C#中的空合并运算符与空合并赋值运算符:简化空值处理
在C#编程中,处理可能为null的值是一项常见的任务,尤其是在涉及数据库查询、Web服务调用或任何可能返回缺失数据的场景中。为了简化这类操作并提高代码的可读性,C# 8 引入了两个非常实用的运算符:空合并运算符 (??) 和 空合并赋值…...

数据结构:哈夫曼树及其哈夫曼编码
目录 1.哈夫曼树是什么? 2.哈夫曼编码是什么? 3.哈夫曼编码的应用 4.包含头文件 5.结点设计 6.接口函数定义 7.接口函数实现 8.哈夫曼编码测试案列 哈夫曼树是什么? 哈夫曼树(Huffman Tree)是一种特殊的二叉树…...
微信如何防止被对方拉黑删除?一招教你解决!文末附软件!
你一定不知道,微信可以防止被对方拉黑删除,秒变无敌。只需一招就能解决!赶快来学!文末有惊喜! 惹到某些重要人物(比如女朋友),被删除拉黑一条龙,那真的是太令人沮丧了&a…...

jar增量打包
jar增量打包 Linux环境下: 1.解压缩 jar -xvf jarname.jar(解压)2.打包 这时可以把要替换的lib包的内容粘帖进去,然后重新打jar包 jar -cvf0M jarname.jar .(重新压缩,-0是主要的)jar命令: …...

智慧医院物联网建设-统一管理物联网终端及应用
近年来,国家卫健委相继出台的政策和评估标准体系中,都涵盖了强化物联网建设的内容。物联网建设已成为智慧医院建设的核心议题之一。 作为医院高质量发展的关键驱动力,物联网的顶层设计与网络架构设计规划,既需要结合现代信息技术的…...

Debian的常用命令
Debian作为一个稳定、安全且高效的Linux发行版,被广泛应用于服务器和桌面操作系统中。对于系统管理员和开发者来说,熟练掌握Debian的常用命令能够大大提升工作的效率和系统的管理水平。本文将详细介绍一些常见且实用的Debian命令,帮助新手更好地管理和操作Debian系统。 系统…...

矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换 1、矩阵1-范数 A [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots …...

Python笔记 - *args和**kwargs
探索Python的*args和**kwargs 在Python中,函数可以接受任意数量的参数,而这要归功于*args和**kwargs的强大功能。这两个特性使得函数在处理不同数量的输入时变得更加灵活和高效。在这篇博客中,我们将详细介绍*args和**kwargs,并展…...

微信小程序实现图片转base64
在微信小程序中,图片转base63可以引入第三方插件; 也可以通过下边的方法转base64。 转换方法: imgToBase64(filePath) {return new Promise((resolve, reject) > {let baseFormat data:image/png;base64,let base64 wx.getFileSystem…...

os和os.path模块
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 目录也称文件夹,用于分层保存文件。通过目录可以分门别类地存放文件。我们也可以通过目录快速找到想要的文件。在Python中,并…...
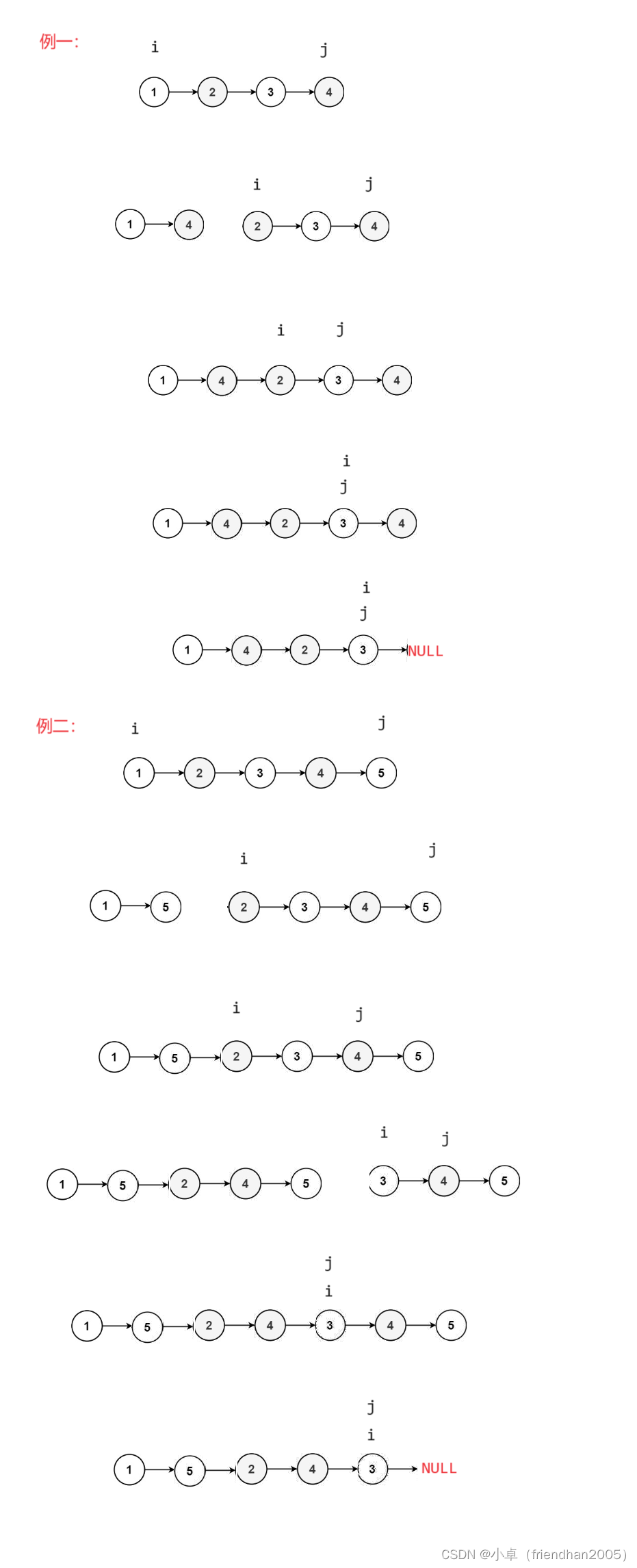
链表题目练习----重排链表
这道题会联系到前面写的一篇文章----快慢指针相关经典问题。 重排链表 指针法 这道题乍一看,好像有点难处理,但如果仔细观察就会发现,这道题是查找中间节点反转链表链表的合并问题,具体细节有些不同,这个在反装中间链…...

【杂记-浅谈XSS跨站脚本攻击】
一、什么是XSS? XSS,Cross-site Scripting,跨站脚本攻击,是一种典型的Web程序漏洞利用攻击,攻击者利用Web程序对用户输入检查不足的漏洞将可执行恶意脚本注入网站或Web应用,当用户访问网页时触发恶意脚本的…...
VMware虚拟机与MobaXterm建立远程连接失败
VMware虚拟机与MobaXterm建立远程连接失败 首先可以检查一下是不是虚拟机的ssh服务并不存在 解决方法: 1.更新镜像源 yum -y update 这个过程会有点久,请耐心等待 2.安装ssh yum install openssh-server 3.启动ssh systemctl restart sshd 4.查…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

GB/T 43887-2024 核级柔性石墨板材检测
核级柔性石墨板材是指以可膨胀石墨为原料、未经改性和增强、用于核工业的核级柔性石墨板材。 GB/T 43887-2024核级柔性石墨板材检测检测指标: 测试项目 测试标准 外观 GB/T 43887 尺寸偏差 GB/T 43887 化学成分 GB/T 43887 密度偏差 GB/T 43887 拉伸强度…...
