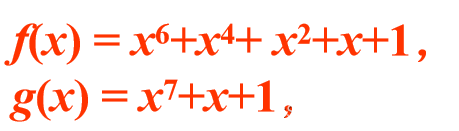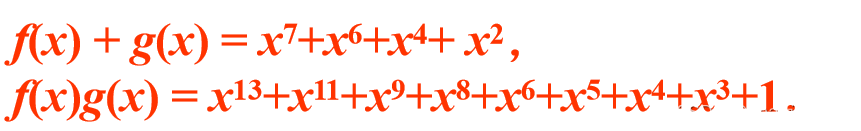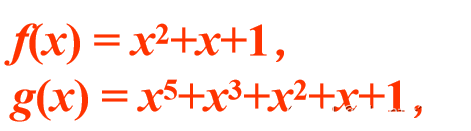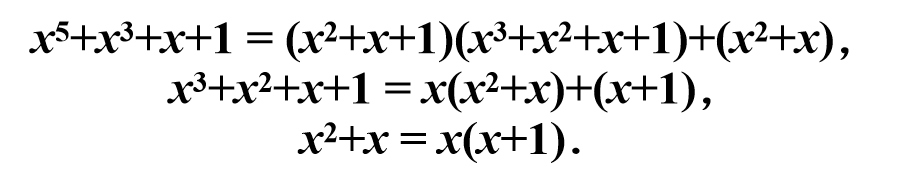网络空间安全数学基础·多项式环与有限域
5.1 多项式环(掌握)
5.2 多项式剩余类环(理解)
5.3 有限域(熟练)
5.1 多项式环
定义:设F是一个域,称![]() 是F上的一元多项式.
是F上的一元多项式.
首项:如果an≠0,则称 anx^n 为f(x)的首项
次数:n是多项式f(x)的次数,记为deg(f(x)) = n
首一多项式:如果an = 1,则称f(x)为首一多项式
零次多项式:若f(x) = a0≠0,则约定deg(f(x)) = 0
F上的全体一元多项式的集合用F[x]表示
零多项式:当ai全为0时,f(x)=0,称为零多项式
多项式环运算
对于F[x]中的任意两个多项式
定义F[x]上的加法和乘法分别如下: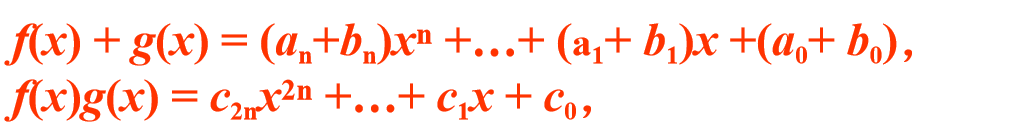
其中
例:域GF(2)上的两个多项式:
则
定理:若F是域,F[x]是具有单位元的整环.
多项式整除
定义:f(x),g(x)∈F[x],f(x)≠0.如果存在q(x)∈F[x],使 g(x) = q(x) f(x),则称f(x)整除g(x),记为 f(x)|g(x), f(x)称为g(x)的因式。如果 f^k(x)|g(x),但f^(k+1)(x)不能整除g(x),则称f(x)是g(x)的k重因式.
多项式整除的性质
多项式整除具有下列性质:其中c≠0∈F.
1) f(x)|0;
2) c|f(x) (因为f(x) = c(c^(-1)f(x)));
3) 如果 f(x)|g(x),则 cf(x)|g(x);
4) 如果 f(x)|g(x),g(x)|h(x),则 f(x)|h(x);
5) 如果 f(x)|g(x),f(x)|h(x),则对任意u(x),v(x)∈F[x],有 f(x)|u(x)g(x)+ v(x)h(x);
6) 如果 f(x)|g(x),g(x)|f(x),则f(x) = cg(x).
例:Z[x]中有
F[x]的带余除法:对f(x),g(x)∈F[x],f(x)≠0,存在q(x),r(x)∈F[x],使例:GF(2)[x]上多项式
则
最大公因式
定义:f(x), g(x)∈F[x]为不全为零多项式.设d(x)≠0∈F[x],如果 d(x)|f(x),d(x)|g(x),则称 d(x) 是 f(x),g(x) 的一个公因式。
若d(x)是首一多项式,而且 f(x), g(x) 的任何公因式都整除d(x),则称d(x)是 f(x), g(x)的最大公因式,记为(f(x),g(x))。
如果(f(x),g(x))=1,则称f(x),g(x)互素。
定理(欧几里德算法):对于多项式f(x),g(x),其中deg(f(x))≤deg(g(x))。反复进行欧几里德除法:
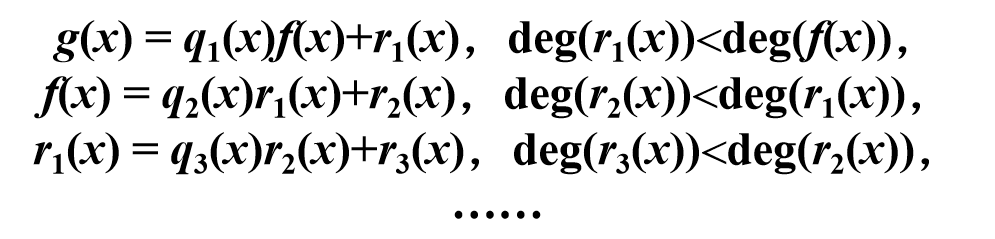

于是![]()
例:求GF(2)[x]上多项式:
解:由欧几里德算法得:
故
定理5-3 对于多项式f(x),g(x),其中deg(f(x))≤deg(g(x)),而且h(x) = (f(x),g(x)).则存在a(x),b(x)使 a(x)f(x)+b(x)g(x)=h(x), 其中deg(a(x))≤deg(g(x)), deg(b(x))≤deg(g(x))
特别地,当f(x),g(x)互素时,存在a(x),b(x)使 a(x)f(x)+b(x)g(x)=1
多项式的分解
定义:设p(x)∈F[x]为首一多项式,且deg(p(x))≥1,如果p(x)在F[x]内的因式仅有零次多项式及cp(x) (c≠0∈F),则称p(x)是F[x]内的一个不可约多项式,否则称为可约多项式。
例:Z[x]上多项式
不可约.GF(2)[x]上多项式
可约:
GF(2)[x]五次以内的不可约多项式:
定理(分解唯一定理):F[x]上的多项式![]() 可分解为
可分解为![]() ,
,![]() 是两两不同的首一不可约多项式.除
是两两不同的首一不可约多项式.除![]() 的排列次序外,上述分解是唯一的。
的排列次序外,上述分解是唯一的。
定理:多项式f(x)∈F[x]含有因式 x∈a (a∈F),当且仅当f(a)=0.
例:分解GF(2)[x]上多项式:
由于f(1)=0,所以f(x)有因式x+1.
运用多项式除法得
通过试探得
故
实际上在GF(2)[x]上有
因此
也可这样分解:
5.2 多项式剩余类环
定义:设f(x)∈F[x]是首一多项式.对于a(x),b(x)∈F[x],如果f(x)除a(x),b(x)得相同的余式,即
则称a(x)和b(x)关于模f(x)同余,记为![]()
由定义可见,a(x)≡b(x) mod f(x)当且仅当 a(x)-b(x)=g(x)f(x),g(x)∈F[x],或 f(x)|a(x)-b(x).
令![]() 是F[x]中关于模f(x)与a(x)同余的全体多项式集合。
是F[x]中关于模f(x)与a(x)同余的全体多项式集合。
与整数情形相似,我们可以把F[x]划分成剩余类,这些剩余类的集合记为F[x] mod f(x)。
例:GF(2)[x]mod
=
定义多项式剩余类的加法和乘法分别如下:
定理:设f(x)∈F[x]是一个首一多项式,且deg(f(x))>0,则F[x]mod f(x)构成具有单位元的交换环,称为多项式剩余类环。多项式剩余类环可能存在零因子,例如GF(2)[x]mod![]() 中就有零因子,因为
中就有零因子,因为![]() 。
。
GF(2)[x]mod ![]() 存在零因子,是因为
存在零因子,是因为![]() 是可约多项式.在不可约多项式情形,我们有下面的定理.
是可约多项式.在不可约多项式情形,我们有下面的定理.
定理:如果f(x)是F上的首一不可约多项式,则F[x]mod f(x)构成域.
定理:域F上的多项式F[x]是主理想整环.
5.3 有限域
定义:有限个元素构成的域称为有限域或Galois(伽罗瓦)域.域中元素的个数称为有限域的阶.
我们曾指出,当p是素数时,模p剩余类集合![]() 构成p阶有限域GF(p) 并指出这也是最简单的一种有限域. q阶有限域的所有非零元构成q-1阶乘法交换群.
构成p阶有限域GF(p) 并指出这也是最简单的一种有限域. q阶有限域的所有非零元构成q-1阶乘法交换群.
我们将域中非零元素关于乘法群的阶定义为域中非零元素的阶.
由关于群的讨论我们有,n阶有限群的任意元素a均满足a^n = 1.所 以a^(q-1)=1。
如果把零元也考虑进来,则q阶有限域的所有元素满足 aq=a,或 aq-a = 0
那么q阶有限域可以看成是方程 x^q-x=0的根的集合。
定义:q阶有限域中阶为q-1的元素称为本原域元素,简称本原元。
本原元的意义是很明显的。如果q阶有限域中存在本原元a,则所有非零元构成一个由a生成的q-1阶循环群.那么q阶有限域就可以表示为![]()
定理:有限域中一定含有本原元。实际上,当q>2时,q阶有限域的本原元多于一个。如果a是一个本原元,对于1≤n≤q-1,只要 (n,q-1) = 1, 由群中的结论,则a^n的阶也是q-1,即a^n也是本原元。我们指出,q阶有限域中共有φ(q-1)个本原元(φ是欧拉函数)。
假设a是域中的一个非零元,使![]() 的最小正整数n是a的加法阶.如果不存在这样的n,则加法阶是无限大.
的最小正整数n是a的加法阶.如果不存在这样的n,则加法阶是无限大.
例:GF(7)非零元素的加法阶:
定理:在一个无零因子环R里所有非零元的加法阶都相同。当加法阶有限时,它是一个素数。
定义:域中非零元的加法阶称为域的特征,当加法阶为无限大时,称特征为0。
推论:域的特征或者是0,或者是一个素数.有限域的特征是素数。
例:GF(p)的特征为p,因为
GF(p)的特征等于| GF(p)|.
定理:有限域的阶必为其特征之幂。一般有限域记为GF(p^m),其中p是域的特征,m是正整数。由于特征总是素数,则有限域的阶总为素数的幂。
定理:如果f(x)是GF(p)上的m次首一不可约多项式,则GF(p)[x] mod f(x)构成pm阶有限域GF(p^m)。
例:GF(2)[x] mod
构成有限域GF(2^3)。
GF(2^3)的8个元素:
为了表示简单,可以去掉上面的横线,但其剩余类的含义没有改变:
相关文章:
网络空间安全数学基础·多项式环与有限域
5.1 多项式环(掌握) 5.2 多项式剩余类环(理解) 5.3 有限域(熟练) 5.1 多项式环 定义:设F是一个域,称是F上的一元多项式. 首项:如果an≠0,则称 a…...
路由器重启真的好吗?多久重启一次更好?
前言 小白前段时间发现自己家的OpenWRT软路由上网特别慢,有时候通话还有点卡顿。 然而有个朋友用的普通路由器也有类似的问题,而且有时候根本上不去网。 解决的办法很简单:重启路由器。 重启路由器? 但路由器重启是真的好吗&a…...

删除目录
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 删除目录可以通过使用os模块提供的rmdir()函数实现。通过rmdir()函数删除目录时,只有当要删除的目录为空时才起作用。rmdir()函数的基本语…...

HCIP-Datacom-ARST自选题库__BGP/MPLS IP VPN判断【10道题】
1.部署BGP/MPLSIP VPN时,当两个VPN有共同的站点,则该共同站点一定不能与两个VPN其他站点使用重叠的地址空间。 2.如图所示,运营商BGP/MPLSIP VPN骨干网通过LDP构建LSP,若想实现用户X两个站点之间通过BGP/MPLSIP VPN网络互通,则PE1和PE2之间必…...

【Go语言精进之路】构建高效Go程序:掌握变量、常量声明法则与iota在枚举中的奥秘
🔥 个人主页:空白诗 文章目录 引言一、变量1.1 基础知识1.2 包级变量的声明形式深入解析📌 声明并同时显式初始化📌 声明但延迟初始化📌 声明聚类与就近原则 1.3 局部变量的声明形式深入探讨📌 延迟初始化的…...

python记录之bool
在Python中,bool 是一个内置的数据类型,用于表示逻辑值:True 或 False。虽然这个数据类型看起来很简单,但在编程中它扮演着至关重要的角色,特别是在条件语句、循环以及许多其他逻辑操作中。以下是对Python bool 的深入…...

加密经济浪潮:探索Web3对金融体系的颠覆
随着区块链技术的快速发展,加密经济正在成为全球金融领域的一股新的浪潮。而Web3作为下一代互联网的代表,以其去中心化、可编程的特性,正深刻影响着传统金融体系的格局和运作方式。本文将深入探讨加密经济对金融体系的颠覆,探索We…...
list的简单模拟实现
文章目录 目录 文章目录 前言 一、使用list时的注意事项 1.list不支持std库中的sort排序 2.去重操作 3.splice拼接 二、list的接口实现 1.源码中的节点 2.源码中的构造函数 3.哨兵位头节点 4.尾插和头插 5.迭代器* 5.1 迭代器中的operator和-- 5.2其他迭代器中的接口 5.3迭代器…...

深入解析Java HashMap的putVal方法
Java中的HashMap是我们在开发中经常使用的集合之一,它提供了基于哈希表的数据存储方式,使得对数据的插入、删除和查找操作都具有较高的效率。在本文中,我们将深入解析HashMap中的putVal方法,揭示其内部工作原理。通过对代码的逐行…...
使用智谱 GLM-4-9B 和 SiliconCloud 云服务快速构建一个编码类智能体应用
本篇文章我将介绍使用智谱 AI 最新开源的 GLM-4-9B 模型和 GenAI 云服务 SiliconCloud 快速构建一个 RAG 应用,首先我会详细介绍下 GLM-4-9B 模型的能力情况和开源限制,以及 SiliconCloud 的使用介绍,最后构建一个编码类智能体应用作为测试。…...
关于vue2 antd 碰到的问题总结下
1.关于vue2 antd 视图更新问题 1.一种强制更新 Vue2是通过用Object…defineProperty来设置数据的getter和setter实现对数据和以及视图改变的监听的。对于数组和对象这种引用类型来说,getter和setter无法检测到它们内部的变化。用这种 this.$set(this.form, "…...

常见的api:Runtime Object
一.Runtiem的成员方法 1.getRuntime() 当前系统的运行环境 2.exit 停止虚拟机 3.avaliableProcessors 获取Cpu线程的参数 4.maxMemory JVM能从系统中获取总内存大小(单位byte) 5.totalMemory JVM已经从系统中获取总内大小(单位byte) 6.freeMemory JVM剩余内存大小(…...

Linux守护进程揭秘-无声无息运行在后台
在Linux系统中,有一些特殊的进程悄无声息地运行在后台,如同坚实的基石支撑着整个系统的运转。它们就是众所周知的守护进程(Daemon)。本文将为你揭开守护进程的神秘面纱,探讨它们的本质特征、创建过程,以及如何重定向它们的输入输出…...
模型基础笔记0.1.096)
python-Bert(谷歌非官方产品)模型基础笔记0.1.096
python-bert模型基础笔记0.1.015 TODOLIST官网中的微调样例代码Bert模型的微调限制Bert的适合的场景Bert多语言和中文模型Bert模型两大类官方建议模型Bert模型中名字的含义Bert模型包含的文件Bert系列模型参数介绍微调与迁移学习区别Bert微调的方式Pre-training和Fine-tuning区…...

Linux的命令补全脚本
一 linux命令补全脚本 Linux的命令补全脚本是一个强大且高效的工具,它能够极大地提高用户在命令行界面的工作效率。这种脚本通过自动完成部分输入的命令或参数,帮助用户减少敲击键盘的次数并降低出错率。接下来将深入探讨其工作原理、安装方式以及如何自…...

前端 JS 经典:打印对象的 bug
1. 问题 相信这个 console 打印语句的 bug,其实小伙伴们是遇到过的,就是你有一个对象,通过 console,打印一次,然后经过一些处理,再通过 console 打印,发现两次打印的结果是一样的,第…...

大型语言模型简介
大型语言模型简介 大型语言模型 (LLM) 是一种深度学习算法,可以使用非常大的数据集识别、总结、翻译、预测和生成内容。 文章目录 大型语言模型简介什么是大型语言模型?为什么大型语言模型很重要?什么是大型语言模型示例?大型语…...

javaWeb4 Maven
Maven-管理和构建java项目的工具 基于POM的概念 1.依赖管理:管理项目依赖的jar包 ,避免版本冲突 2.统一项目结构:比如统一eclipse IDEA等开发工具 3.项目构建:标准跨平台的自动化项目构建方式。有标准构建流程,能快速…...

eclipse连接后端mysql数据库并且查询
教学视频:https://www.bilibili.com/video/BV1mK4y157kE/?spm_id_from333.337.search-card.all.click&vd_source26e80390f500a7ceea611e29c7bcea38本人eclipse和up主不同的地方如下,右键项目名称->build path->configure build path->Libr…...
Windows mstsc
windows mstsc 局域网远程计算机192.168.0.113为例,远程控制命令mstsc...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...