【机器学习300问】110、什么是Lasso回归模型?
LASSO回归的全称是Least Absolute Shrinkage and Selection Operator,中文叫“最小绝对收缩和选择算子”,用一个比喻来初步感受一下它的作用:
想象你在整理一个杂乱无章的房间,里面堆满了各种物品(代表众多的预测变量),有些物品对你来说很有价值(真正影响结果的变量),而有些则是可有可无的杂物(与结果关系不大或无关的变量)。Lasso回归就像是一个高效的空间整理师,它不仅帮你整理出最重要的几样物品,还会把那些不重要的杂物直接扔出门外,让你的房间变得干净整洁,同时也更容易找到你需要的东西。
Lasso回归可以有效应对多重共线性问题,即使在预测变量高度相关的情况下也能表现良好。
一、Lasso回归的原理
(1)数学表达
在这个表达式中:
第一部分:是回归模型的均方误差(MSE)
第二部分:是参数向量的L1范数乘以一个调节参数α
代表样本的数量,
代表自变量的数量,
代表因变量的第i个观测值,
代表第j个回归系数,
代表第i个观测的第j个自变量的值。α是正则化参数,它控制着L1惩罚的强度。
(2)文字说明
LASSO的目标函数包括数据拟合项和惩罚项,其中惩罚项是系数的L1范数,这使得部分系数严格收缩到零,从而实现自动的特征选择。
Lasso回归的目标是最小化误差平方和,同时施加所有系数的绝对值之和的惩罚。这种类型的正则化(L1正则化)可以导致系数的某些估计值精确地等于0。这意味着,Lasso回归可以有效地进行变量选择,并确定最重要的变量。L1正则化有助于处理特征数量可能多于样本数量的问题,防止模型过拟合,并且可以增强模型的预测能力。
这个过程就好比是用一根神奇的橡皮筋绑在所有物品上,然后逐渐拉紧。对于那些不那么重要的物品(即对预测结果贡献小的变量),橡皮筋会直接把它们的“价值”(系数)拉到零,仿佛它们从未存在过,从而实现了变量的选择性剔除;而对于关键物品(重要变量),即便橡皮筋拉得很紧,它们依然能保持一定的“体积”(非零系数),因为它们对房间的布局(模型结果)至关重要。
Lasso的L1惩罚项尤其在变量的数量很大时有用,当中只有少数几个因素实际影响响应变量,因此该方法能够自动进行特征选择并输出一个简洁模型。一个合适的α值可以通过交叉验证获得,α的最佳值应平衡误差平方和的减少和模型复杂度的降低(即系数的稀疏性)。
二、Lasso回归的局限性
Lasso回归非常强大,拥有特征选择、处理多重共线性等优点,但也存在局限性:
(1)计算成本与速度
Lasso回归没有显式解,这意味着不能像求解普通线性回归那样直接得到参数估计。相反,需要依赖迭代算法,如坐标下降法或最小角回归等。这些算法虽然有效,但相比有显式解的方法,计算成本较高,尤其是在处理大规模数据集时,可能会显得较慢。
(2)连续型变量的处理
Lasso回归采用的L1范数惩罚可能导致对连续型变量的变化非常敏感。即使变量的小幅变动也可能引起系数的大幅度变化,有时甚至将重要变量的系数“挤压”至零,这可能不是我们期望的结果。相比之下,岭回归使用L2范数惩罚,对连续变量的处理更为温和。
(3)变量选择的不稳定性
Lasso回归在变量选择上的结果可能不稳定,特别是当存在多个高度相关的预测变量时。数据的微小变化或正则化参数λ的轻微调整都可能导致选入或排除的变量发生变化,这种现象被称为“阈值效应”。
(4)系数的非唯一性
在某些情况下,Lasso回归得到的系数解可能不是唯一的,特别是当存在多个变量高度相关时。这增加了结果解释的难度。虽然Lasso可以减少模型的复杂度,避免过拟合,但过度的正则化(即选择较大的λ值)可能会引入偏差,导致模型欠拟合,即无法充分捕捉数据的真实结构。尽管稀疏性是Lasso的一个吸引人的特性,它意味着模型只保留少数重要的特征,但在某些场景下,如果所有的特征都对预测有贡献,过于追求稀疏性可能会牺牲模型的预测性能。
相关文章:
【机器学习300问】110、什么是Lasso回归模型?
LASSO回归的全称是Least Absolute Shrinkage and Selection Operator,中文叫“最小绝对收缩和选择算子”,用一个比喻来初步感受一下它的作用: 想象你在整理一个杂乱无章的房间,里面堆满了各种物品(代表众多的预测变量&…...

Qt实现麦克风音频输入保存wav文件
一.本文目的 实现在Qt中接收麦克风数据并保存为WAV文件,使用QAudioInput来录音,并使用QFile来保存数据到WAV文件。 开发环境:QT5.12 本文用极简代码实现,核心代码只需不到100行。 完整工程代码文末链接可以直接下载。 二.代码实…...
)
docker_如何推送镜像到仓库(hub.docker.com)
在执行 docker push 时收到 denied: requested access to the resource is denied 错误通常意味着你没有权限将镜像推送到目标存储库。这可能有几个原因,包括: 未登录 Docker Hub:你还没有登录到 Docker Hub,或者你登录的账户没有权限推送到目标存储库。存储库不存在:目标…...

【Python】认识 Python
一、计算机基础概念 1、什么是计算机 很多老一辈的人,管下面这个叫做计算机。然而,它只是 “计算器”,和计算机是有很大区别的。 现在我们所说的计算机,不光能进行算术运算,还能进行逻辑判断、数据存储、网络通信等…...

Vue根据后端返回的tabList动态渲染组件信息
最近做了一个功能,后端根据配置信息,动态返回一个tabList,其中结构是List<String,Object> tabList; map里面的数据是 label、value 页面需要根据tablist动态渲染组件(不同的tab都使用了组件进行了封装) 实现效果…...

二轴机器人大米装箱机:技术创新引领智能包装新潮流
在科技日新月异的今天,自动化和智能化已成为各行各业追求高效、精准生产的关键。作为粮食加工行业的重要一环,大米装箱机的技术创新与应用价值日益凸显。其中,二轴机器人大米装箱机以其高效、稳定、智能的特点,成为市场的新宠。星…...
rtl8723DU移植 android4.4 4418 (第二部分蓝牙部分)
使用的代码: HMI (8723bu)源码 567_RTL8723DU_WiFi_linux_v5.6.5.3_35502_COEX20181130-2e2e.20191025.zip 由于之前写的所有笔记没有保存,这里只能是部分。 0、 前置知识 1 、kernel 的移植 2、hardwire的移植 将 驱动中的 h…...
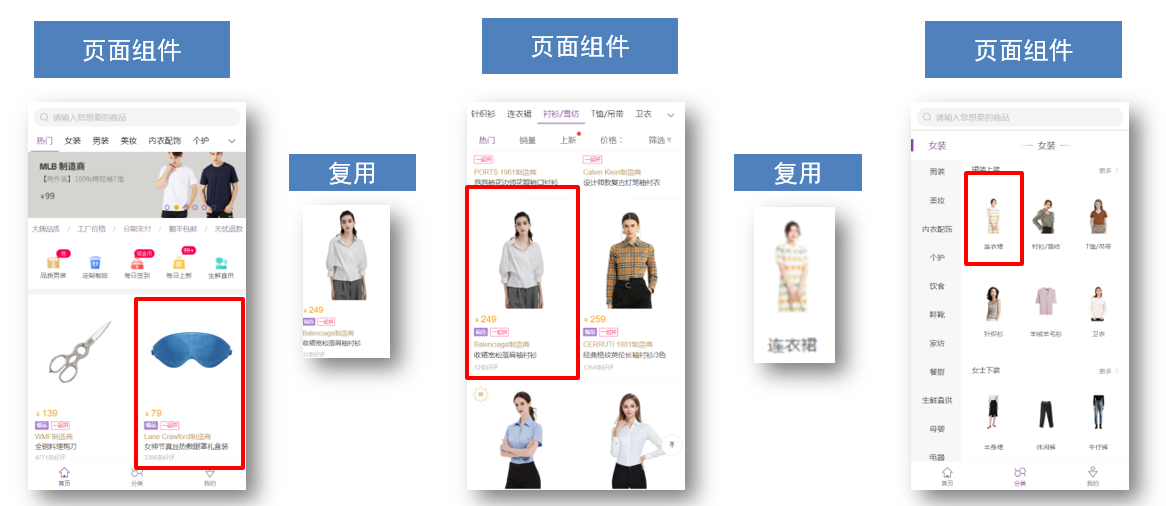
【Vue】组件的存放目录问题
注意: .vue文件 本质无区别 组件分类 .vue文件分为2类,都是 .vue文件(本质无区别) 页面组件 (配置路由规则时使用的组件)复用组件(多个组件中都使用到的组件) 存放目录 分类开来的…...

开发PlugLink插件:自动生成并发布博客文章
开发PlugLink插件:自动生成并发布博客文章 引言 博客已经成为个人和企业分享信息、推广产品的重要工具。然而,手动运营博客不仅耗时,而且容易出错。本文将介绍如何利用PlugLink开发一个全自动博客运营程序,通过API链接大模型&am…...
Ant Design Pro
一:Ant Design pro是什么: Ant Design Pro 是基于 Ant Design 和 umi 的封装的一整套企业级中后台前端/设计解决方案,致力于在设计规范和基础组件的基础上,继续向上构建,提炼出典型模板/业务组件/配套设计资源&#x…...

加密软件好用的是哪个?为什么这么多人说迅软DSE加密软件好用?
加密软件顾名思义就是用来对机密文件进行加密保护的,防止未经授权的人查看和篡改,保护公司的重要信息,预防泄露的事件发生,由此可见运用加密软件是有用的。那么,问题又来了哪款加密软件好呢?请看一下介绍。…...

大模型日报2024-06-07
大模型日报 2024-06-07 大模型资讯 大规模单细胞转录组学基础模型研究 摘要: 大型预训练模型已成为基础模型,在自然语言处理及相关领域取得突破。本文介绍了在单细胞转录组学领域应用大规模基础模型的研究进展。 MMLU-Pro:评估语言理解模型的新基准 摘要…...
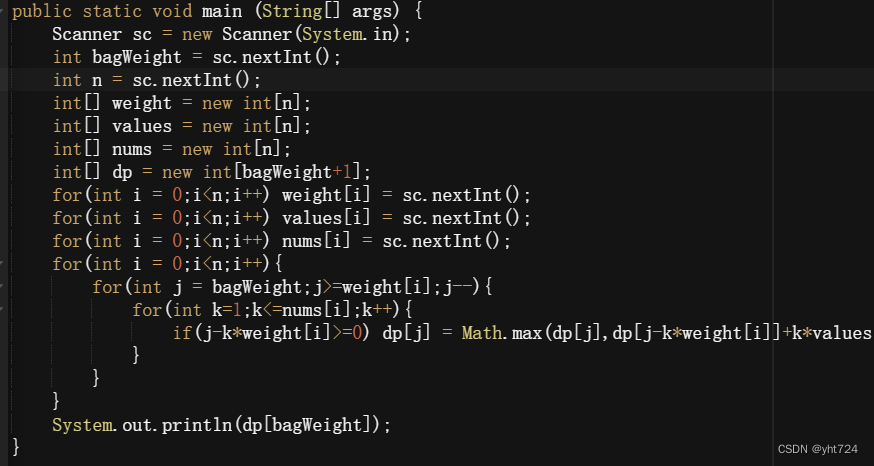
Day49 动态规划part08
LC139单词拆分(未掌握) 未掌握分析:将字符串s中的各个字符看成是背包,思考成了多重背包问题单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。拆分时可以重复使用字典中的单词…...
React -- memo允许你的组件在 props 没有改变的情况下跳过重新渲染。
memo(Component, arePropsEqual?) 使用 memo 将组件包装起来,以获得该组件的一个 记忆化 版本。通常情况下,只要该组件的 props 没有改变,这个记忆化版本就不会在其父组件重新渲染时重新渲染。但 React 仍可能会重新渲染它:记忆化…...

路径
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 用于定位一个文件或者目录的字符串被称为一个路径。在程序开发时,通常涉及两种路径,一种是相对路径,另一种是绝对…...

逆波兰表达式
目录 一、定义 二、算法步骤 三、代码实现 一、定义 逆波兰表达式又叫做后缀表达式,是一种没有括号,并严格遵循“从左到右”运算的后缀式表达方法。 二、算法步骤 1、首先构造一个运算符栈,此运算符在栈内遵循越往栈顶优先级越高的原则。 …...
git(其六)--总结
配置基础信息 //1.配置用户名和邮箱 git config --global user.name "带着引号写一个昵称" git config --global user.email "带着引号写一个邮箱"//2.建立一个git本地库 git init//3.查看本地内容 git status //可以看到那些处于待加入本地库的文件&a…...

kafka-生产者拦截器(SpringBoot整合Kafka)
文章目录 1、生产者拦截器1.1、创建生产者拦截器1.2、KafkaTemplate配置生产者拦截器1.3、使用Java代码创建主题分区副本1.4、application.yml配置----v1版1.5、屏蔽 kafka debug 日志 logback.xml1.6、引入spring-kafka依赖1.7、控制台日志 1、生产者拦截器 1.1、创建生产者拦…...

每日一题:聊聊 Redis 过期键的删除策略
聊聊 Redis 过期键的删除策略 答案 惰性删除 :只会在取出 key 的时候才对数据进行过期检查;这样对 CPU 最友好,但是可能会造成太多过期 key 没有被删除(占用内存)。 通过定时器实现(时间事件)&…...

边缘计算的AI小板——OrangePi AI Pro
简介 OrangePi AI Pro是一款基于Allwinner H6处理器的嵌入式AI计算设备,适用于物联网和边缘计算。它具有强大的性能、低功耗、多接口和小尺寸。 本文分为三个部分: 一、对该板进行简单的开箱介绍。 二、 将SD卡中的系统迁移到由于该板支持SD卡、SSD…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
