代码随想录算法训练营day54 | 动态规划之子序列 392.判断子序列 115.不同的子序列
day54
- 392.判断子序列
- 1.确定dp数组(dp table)以及下标的含义
- 2.确定递推公式
- 3.dp数组如何初始化
- 4.确定遍历顺序
- 5.举例推导dp数组
- 115.不同的子序列
- 1.确定dp数组(dp table)以及下标的含义
- 2.确定递推公式
- 3.dp数组如何初始化
- 4.确定遍历顺序
- 5.举例推导dp数组
392.判断子序列
题目链接
**解题思路:**动态规划五部曲分析如下:
1.确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。
有同学问了,为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
2.确定递推公式
在确定递推公式的时候,首先要考虑如下两种操作,整理如下:
- if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
- if (s[i - 1] != t[j - 1])
- 相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(如果不理解,在回看一下dp[i][j]的定义)
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
3.dp数组如何初始化
从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],所以dp[0][0]和dp[i][0]是一定要初始化的。
这里大家已经可以发现,在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:
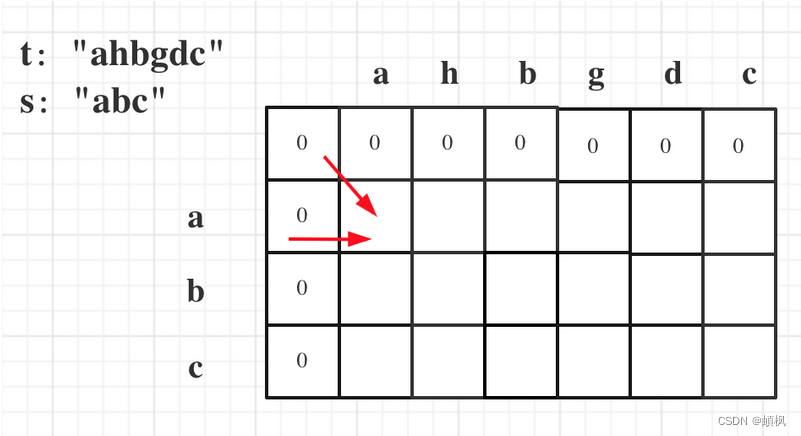
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
dp[i][0] 表示以下标i-1为结尾的字符串,与空字符串的相同子序列长度,所以为0. dp[0][j]同理。
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
4.确定遍历顺序
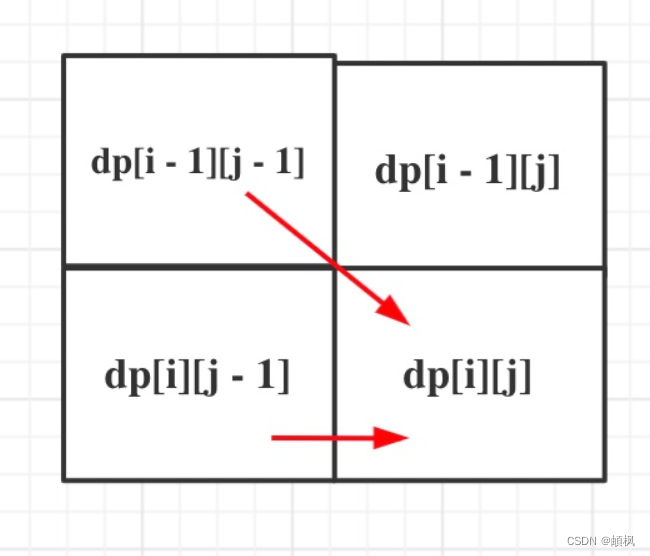
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],那么遍历顺序也应该是从上到下,从左到右
如图所示:
5.举例推导dp数组
以示例一为例,输入:s = “abc”, t = “ahbgdc”,dp状态转移图如下:
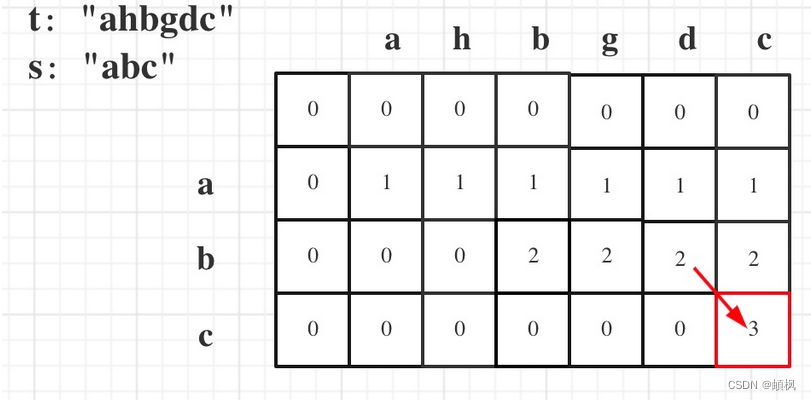
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
图中dp[s.size()][t.size()] = 3, 而s.size() 也为3。所以s是t 的子序列,返回true。
动规五部曲分析完毕,C++代码如下:
class Solution {
public:bool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = dp[i][j - 1];}}if (dp[s.size()][t.size()] == s.size()) return true;return false;}
};
115.不同的子序列
题目链接
解题思路:
动规五部曲分析如下:
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
2.确定递推公式
这一类问题,基本是要分析两种情况
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要 dp[i-1][j-1]。
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
例如: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配,即用s[0]s[1]s[2]组成的bag。
当然也可以用s[3]来匹配,即:s[0]s[1]s[3]组成的bag。
所以当s[i - 1] 与 t[j - 1]相等时,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
当s[i - 1] 与 t[j - 1]不相等时,dp[i][j]只有一部分组成,不用s[i - 1]来匹配(就是模拟在s中删除这个元素),即:dp[i - 1][j]
所以递推公式为:dp[i][j] = dp[i - 1][j];
3.dp数组如何初始化
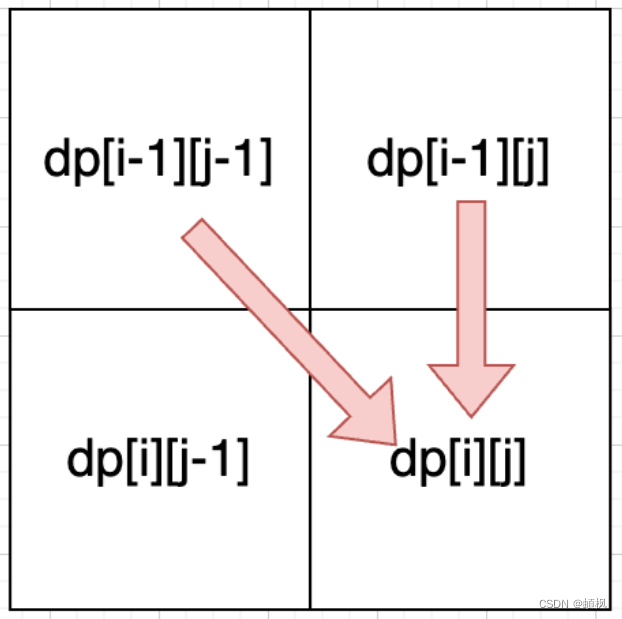
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。
每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
dp[i][0]表示什么呢?
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
再来看dp[0][j],dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。
那么dp[0][j]一定都是0,s如论如何也变成不了t。
最后就要看一个特殊位置了,即:dp[0][0] 应该是多少。
dp[0][0]应该是1,空字符串s,可以删除0个元素,变成空字符串t。
初始化分析完毕,代码如下:
vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和dp数组初始化的时候放在一起,但我为了凸显初始化的逻辑,所以还是加上了。
4.确定遍历顺序
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。
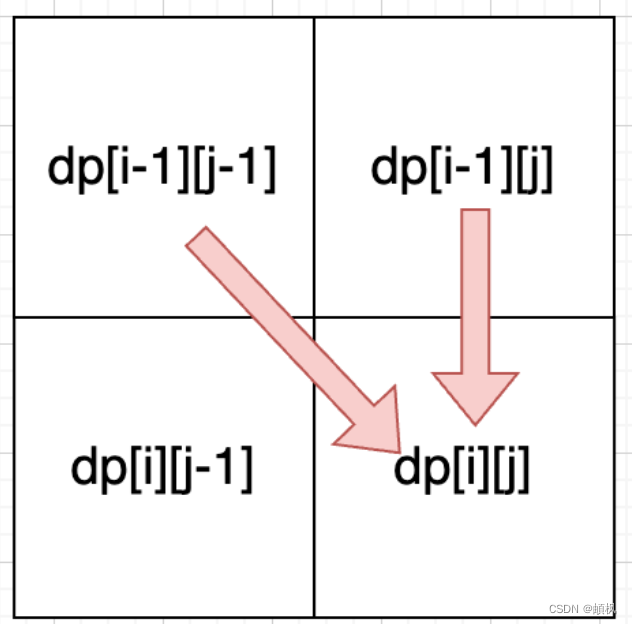
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
代码如下:
for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}}
}
5.举例推导dp数组
以s:“baegg”,t:"bag"为例,推导dp数组状态如下:

动规五部曲分析完毕,代码如下:
class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));for (int i = 0; i < s.size(); i++) dp[i][0] = 1;for (int j = 1; j < t.size(); j++) dp[0][j] = 0;for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}}}return dp[s.size()][t.size()];}
};
相关文章:

代码随想录算法训练营day54 | 动态规划之子序列 392.判断子序列 115.不同的子序列
day54392.判断子序列1.确定dp数组(dp table)以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组115.不同的子序列1.确定dp数组(dp table)以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺…...
:Port与Dio配置)
MCAL知识点(三):Port与Dio配置
目录 1、概述 2、 Port的EB-tresos配置 2.1、创建模块 2.2 General配置 2.3、PortCnfigSet 2.4、Port的属性...

初识C++需要了解的一些东西(1)
目录🥇命名空间🏅存在原因🏵命名空间定义🎧命名空间的3种使用方式🏆C输入和输出🌝缺省参数🌜缺省参数概念⭐️缺省参数分类☀️函数重载🔥引用🌚引用概念🌓引…...

友元函数的使用大全
概述 我们知道,C的类具有封装和信息隐藏的特性。一般情况下,我们会封装public的成员函数供用户调用,而将成员变量设置为private或protected。但在一些比较复杂的业务情况下,可能需要去访问对象中大量的private或protected成员变量…...
QT学习笔记-QT多项目系统中如何指定各项目的编译顺序
QT学习笔记-QT多项目系统中如何指定各项目的编译顺序背景环境解决思路具体操作背景 为了更好的复用程序功能以及更优雅的管理程序,有经验的程序员通常要对程序进行分层和模块化设计。在QT/C这个工具中同样可以通过创建子项目的方式对程序进行模块化,在这…...

JWT令牌解析及刷新令牌(十一)
写在前面:各位看到此博客的小伙伴,如有不对的地方请及时通过私信我或者评论此博客的方式指出,以免误人子弟。多谢!如果我的博客对你有帮助,欢迎进行评论✏️✏️、点赞👍👍、收藏⭐️⭐️&#…...
Hibernate学习(一)
Hibernate学习(一) Hibernate框架的概述: 一:什么是框架:指软件的半成品,已经完成了部分功能。 二:EE的三层架构: 1.EE的三层经典架构: 我在这里主要学的是ssh框架。 三…...

Go的 context 包的使用
文章目录背景简介主要方法获得顶级上下文当前协程上下文的操作创建下级协程的Context场景示例背景 在父子协程协作过程中, 父协程需要给子协程传递信息, 子协程依据父协程传递的信息来决定自己的操作. 这种需求下可以使用 context 包 简介 Context通常被称为上下文ÿ…...
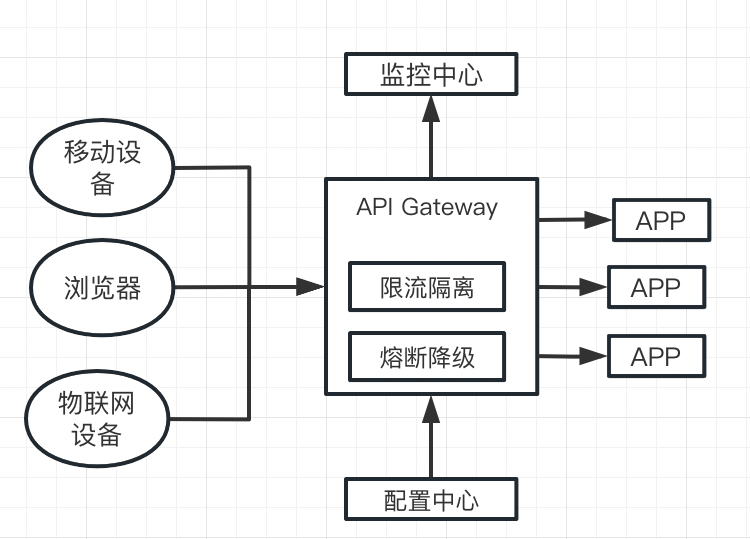
微服务为什么要用到 API 网关?
本文介绍了 API 网关日志的价值,并以知名网关 Apache APISIX 为例,展示如何集成 API 网关日志。 作者程小兰,API7.ai 技术工程师,Apache APISIX Contributor。 原文链接 什么是微服务 微服务架构(通常简称为微服务&a…...

SWUST OJ 1042: 中缀表达式转换为后缀表达式【表达式转逆波兰表达式】
题目描述 中缀表达式是一个通用的算术或逻辑公式表示方法,操作符是以中缀形式处于操作数的中间(例:3 4),中缀表达式是人们常用的算术表示方法。后缀表达式不包含括号,运算符放在两个运算对象的后面&#…...

Matlab基础知识
MATLAB批量读入文件和导出文件一、 批量读入文件1.若文件名称有序,则按照文件名称规律循环读取文件(1)读入不同的excelfor i1:1:10strstrcat(F:\数据\v,int2str(i),.xlsx); %连接字符串形成文件名Axlsread(str); end注:变量i为整数时,可以用i…...

动手学深度学习【2】——softmax回归
动手学深度学习网址:动手学深度学习 注:本部分只对基础知识进行简单的介绍并附上完整的代码实现,更多内容可参考上述网址。 前言 前面一节我们谈到了线性回归,它解决的是预测某个值的问题。但是在日常生活这,除了预测…...

深入理解Activity的生命周期
之前学习安卓的时候只是知道生命周期是什么,有哪几个,但具体的详细的东西却不知道,后来看过《Android开发艺术探索》和大量博客之后,才觉得自己真正有点理解生命周期,本文是我对生命周期的认识的总结。废话少说先上图。…...

Go语言刷题常用数据结构和算法
数据结构 字符串 string 访问字符串中的值 通过下标访问 s1 : "hello world"first : s[0]通过切片访问 s2 : []byte(s1) first : s2[0]通过for-range循环访问 for i, v : range s1 {fmt.Println(i, v) }查询字符是否属于特定字符集 // 判断字符串中是否包含a、b、…...

深入vue2.x源码系列:手写代码来模拟Vue2.x的响应式数据实现
前言 Vue响应式原理由以下三个部分组成: 数据劫持:Vue通过Object.defineProperty()方法对data中的每个属性进行拦截,当属性值发生变化时,会触发setter方法,通知依赖更新。发布-订阅模式:Vue使用发布-订阅…...
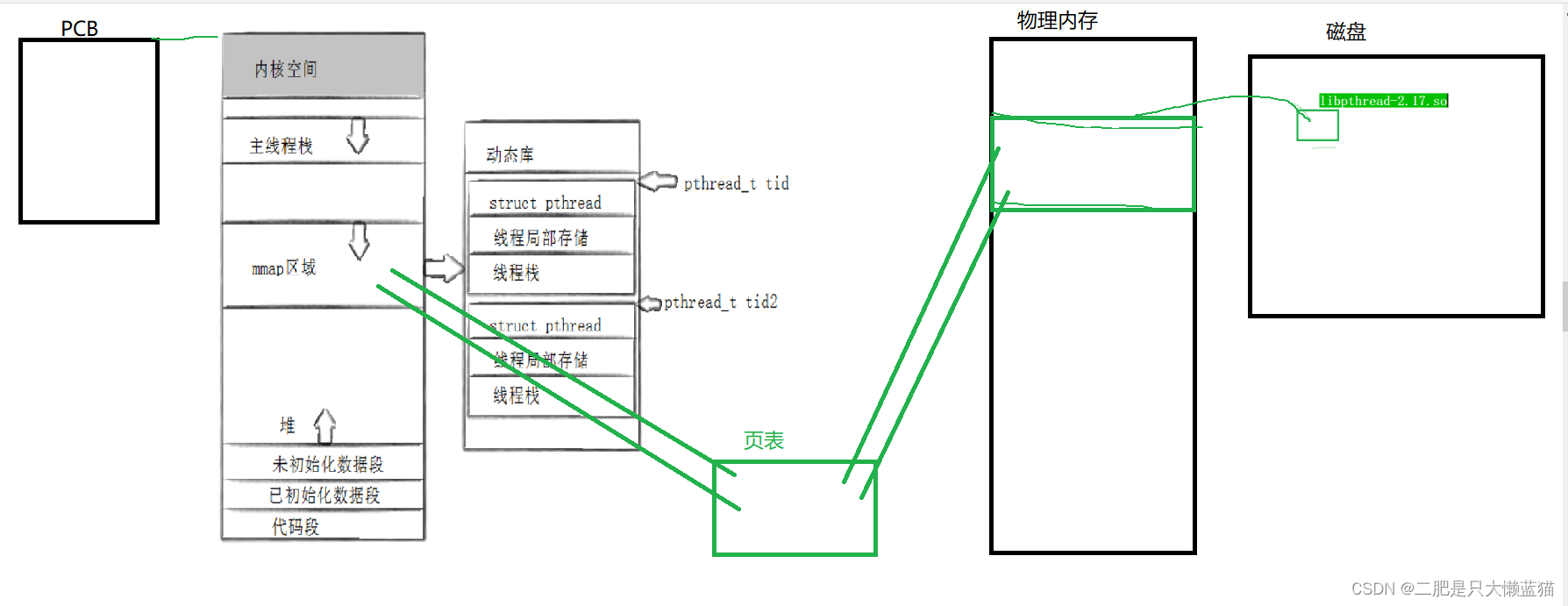
Linux线程控制
本篇我将学习如何使用多线程。要使用多线程,因为Linux没有给一般用户直接提供操作线程的接口,我们使用的接口,都是系统工程师封装打包成原生线程库中的。那么就需要用到原生线程库。因此,需要引入-lpthread,即连接原生…...

【LeetCode】剑指 Offer(20)
目录 题目:剑指 Offer 38. 字符串的排列 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer 38. 字符串的…...
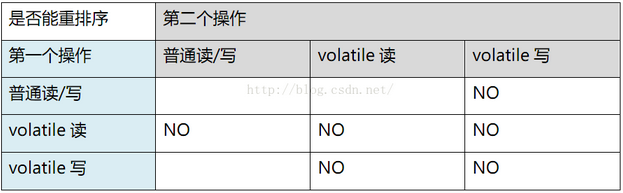
FutureTask中的outcome字段是如何保证可见性的?
最近在阅读FutureTask的源码是发现了一个问题那就是源码中封装结果的字段并没有使用volatile修饰,源码如下:public class FutureTask<V> implements RunnableFuture<V> {/*** 状态变化路径* Possible state transitions:* NEW -> COMPLET…...

直播回顾 | 聚焦科技自立自强,Bonree ONE 助力国产办公自动化平稳替代
3月5日,两会发布《政府工作报告》,强调科技政策要聚焦自立自强。 统计显示,2022年金融信创项目数同比增长300%,金融领域信创建设当前已进入发展爆发期,由国有大型银行逐渐向中小型银行、非银金融机构不断扩展。信创云…...

深入理解Linux进程
进程参数和环境变量的意义一般情况下,子进程的创建是为了解决某个问题。那么解决问题什么问题呢?这个就需要进程参数和环境变量来进行决定的。子进程解决问题需要父进程的“数据输入”(进程参数 & 环境变量)设计原则:3.1 子进程启动的时候…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
