SWUST OJ 1042: 中缀表达式转换为后缀表达式【表达式转逆波兰表达式】
题目描述
中缀表达式是一个通用的算术或逻辑公式表示方法,操作符是以中缀形式处于操作数的中间(例:3 + 4),中缀表达式是人们常用的算术表示方法。后缀表达式不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行(不再考虑运算符的优先规则,如:(2 + 1) * 3 , 即2 1 + 3 *。利用栈结构,将中缀表达式转换为后缀表达式。(测试数据元素为单个字符)
输入
中缀表达式
输出
后缀表达式
样例输入复制
A+(B-C/D)*E
样例输出复制
ABCD/-E*+
这个题我看到解法当中有通过编译原理当中的文法表达式来处理的,也有用堆栈模拟的。
我的方案是用递归。
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<vector>
#include<string>
#include<map>
#include<queue>
#include<iostream>
#include<list>
#include<set>
#include<stack>using namespace std;bool expr_cut(string root_expr,vector<string>& expr_list,vector<char>& op_list)
{stack<int> s;int len=root_expr.size();if(len==1)return true;string expr_now;bool first_flag=false,second_flag=false;for(int i=0;i<len;++i){if((root_expr[i]=='+' || root_expr[i]=='-') && s.empty()){expr_list.push_back(expr_now);op_list.push_back(root_expr[i]);expr_now.clear();first_flag=true;continue;}else if(root_expr[i]=='('){s.push(i);}else if(root_expr[i]==')'){s.pop();}expr_now=expr_now+root_expr[i];}expr_list.push_back(expr_now);if(first_flag)return false;expr_list.clear(),op_list.clear(),expr_now.clear();for(int i=0;i<len;++i){if((root_expr[i]=='*' || root_expr[i]=='/') && s.empty()){expr_list.push_back(expr_now);op_list.push_back(root_expr[i]);expr_now.clear();second_flag=true;continue;}else if(root_expr[i]=='('){s.push(i);}else if(root_expr[i]==')'){s.pop();}expr_now=expr_now+root_expr[i];}expr_list.push_back(expr_now);if(second_flag)return false;expr_list.clear(),op_list.clear(),expr_now.clear();root_expr=root_expr.substr(1,root_expr.size()-2);return expr_cut(root_expr,expr_list,op_list);
}string f(string root_expr)
{vector<string> expr_list;vector<char> op_list;bool is_atom=expr_cut(root_expr,expr_list,op_list);if(is_atom)return root_expr;else{string result="";string first_item=f(expr_list[0]);for(int i=1;i<expr_list.size();i++){string second_item=f(expr_list[i]);result=first_item+second_item+result+op_list[i-1];first_item=second_item;}return result;}
}int main()
{string expr;while(cin>>expr){string result=f(expr);cout<<result;}return 0;
}/*
A+B*C-(D*F*(F+B+C*D)-(A*H))*T
(A+B*C)
*/相关文章:

SWUST OJ 1042: 中缀表达式转换为后缀表达式【表达式转逆波兰表达式】
题目描述 中缀表达式是一个通用的算术或逻辑公式表示方法,操作符是以中缀形式处于操作数的中间(例:3 4),中缀表达式是人们常用的算术表示方法。后缀表达式不包含括号,运算符放在两个运算对象的后面&#…...

Matlab基础知识
MATLAB批量读入文件和导出文件一、 批量读入文件1.若文件名称有序,则按照文件名称规律循环读取文件(1)读入不同的excelfor i1:1:10strstrcat(F:\数据\v,int2str(i),.xlsx); %连接字符串形成文件名Axlsread(str); end注:变量i为整数时,可以用i…...

动手学深度学习【2】——softmax回归
动手学深度学习网址:动手学深度学习 注:本部分只对基础知识进行简单的介绍并附上完整的代码实现,更多内容可参考上述网址。 前言 前面一节我们谈到了线性回归,它解决的是预测某个值的问题。但是在日常生活这,除了预测…...

深入理解Activity的生命周期
之前学习安卓的时候只是知道生命周期是什么,有哪几个,但具体的详细的东西却不知道,后来看过《Android开发艺术探索》和大量博客之后,才觉得自己真正有点理解生命周期,本文是我对生命周期的认识的总结。废话少说先上图。…...

Go语言刷题常用数据结构和算法
数据结构 字符串 string 访问字符串中的值 通过下标访问 s1 : "hello world"first : s[0]通过切片访问 s2 : []byte(s1) first : s2[0]通过for-range循环访问 for i, v : range s1 {fmt.Println(i, v) }查询字符是否属于特定字符集 // 判断字符串中是否包含a、b、…...

深入vue2.x源码系列:手写代码来模拟Vue2.x的响应式数据实现
前言 Vue响应式原理由以下三个部分组成: 数据劫持:Vue通过Object.defineProperty()方法对data中的每个属性进行拦截,当属性值发生变化时,会触发setter方法,通知依赖更新。发布-订阅模式:Vue使用发布-订阅…...
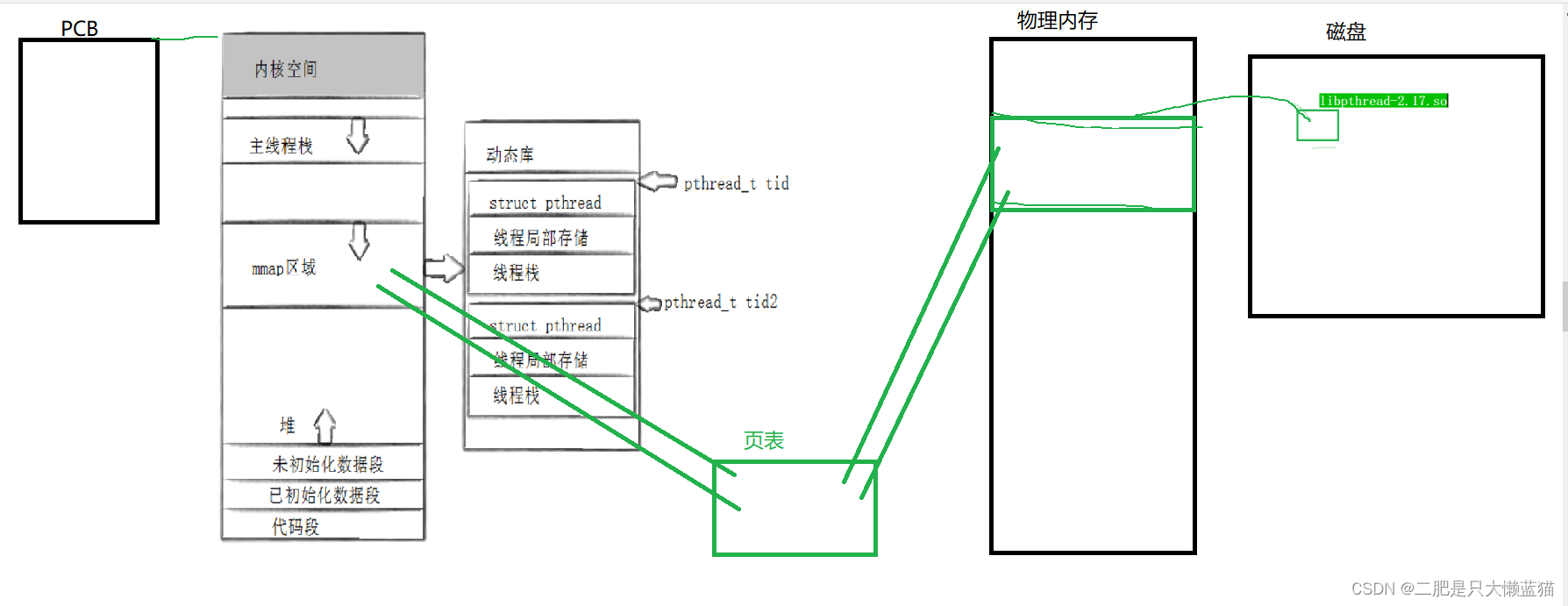
Linux线程控制
本篇我将学习如何使用多线程。要使用多线程,因为Linux没有给一般用户直接提供操作线程的接口,我们使用的接口,都是系统工程师封装打包成原生线程库中的。那么就需要用到原生线程库。因此,需要引入-lpthread,即连接原生…...

【LeetCode】剑指 Offer(20)
目录 题目:剑指 Offer 38. 字符串的排列 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer 38. 字符串的…...
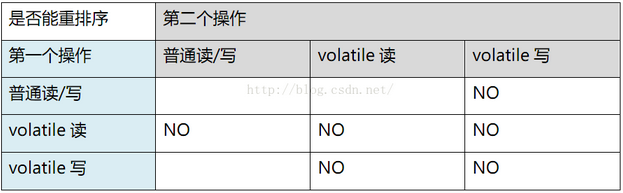
FutureTask中的outcome字段是如何保证可见性的?
最近在阅读FutureTask的源码是发现了一个问题那就是源码中封装结果的字段并没有使用volatile修饰,源码如下:public class FutureTask<V> implements RunnableFuture<V> {/*** 状态变化路径* Possible state transitions:* NEW -> COMPLET…...

直播回顾 | 聚焦科技自立自强,Bonree ONE 助力国产办公自动化平稳替代
3月5日,两会发布《政府工作报告》,强调科技政策要聚焦自立自强。 统计显示,2022年金融信创项目数同比增长300%,金融领域信创建设当前已进入发展爆发期,由国有大型银行逐渐向中小型银行、非银金融机构不断扩展。信创云…...

深入理解Linux进程
进程参数和环境变量的意义一般情况下,子进程的创建是为了解决某个问题。那么解决问题什么问题呢?这个就需要进程参数和环境变量来进行决定的。子进程解决问题需要父进程的“数据输入”(进程参数 & 环境变量)设计原则:3.1 子进程启动的时候…...

Vue3之组件间的双向绑定
何为组件间双向绑定 我们都知道当父组件改变了某个值后,如果这个值传给了子组件,那么子组件也会自动跟着改变,但是这是单向的,使用v-bind的方式,即子组件可以使用父组件的值,但是不能改变这个值。组件间的…...

Java语法基础(一)
目录 代码注释方法 编码规范 基本数据类型及取值范围 变量和常量的声明与赋值 变量 常量 标识符 基本数据类型的使用 整数类型的使用 浮点类型的使用 布尔类型的使用 字符类型的使用 代码注释方法 单行注释:使用“//”进行单行注释多行注释:使…...

优思学院|零质量控制是什么概念?
零质量控制(Zero Quality Control)是指一个理想的系统,可以生产没有任何缺陷的产品,因此不需要频繁的检查,从而节省时间和金钱。那些追求过程优化并致力于持续过程改进的组织将零质量控制(Zero Quality Con…...

2023-03-09 CMU15445-Query Execution
摘要: CMU15445, Project #3 - Query Execution 参考: Project #3 - Query Execution | CMU 15-445/645 :: Intro to Database Systems (Fall 2022) https://github.com/cmu-db/bustub 要求: OVERVIEW At this point in the semester, you have implemented the internal co…...
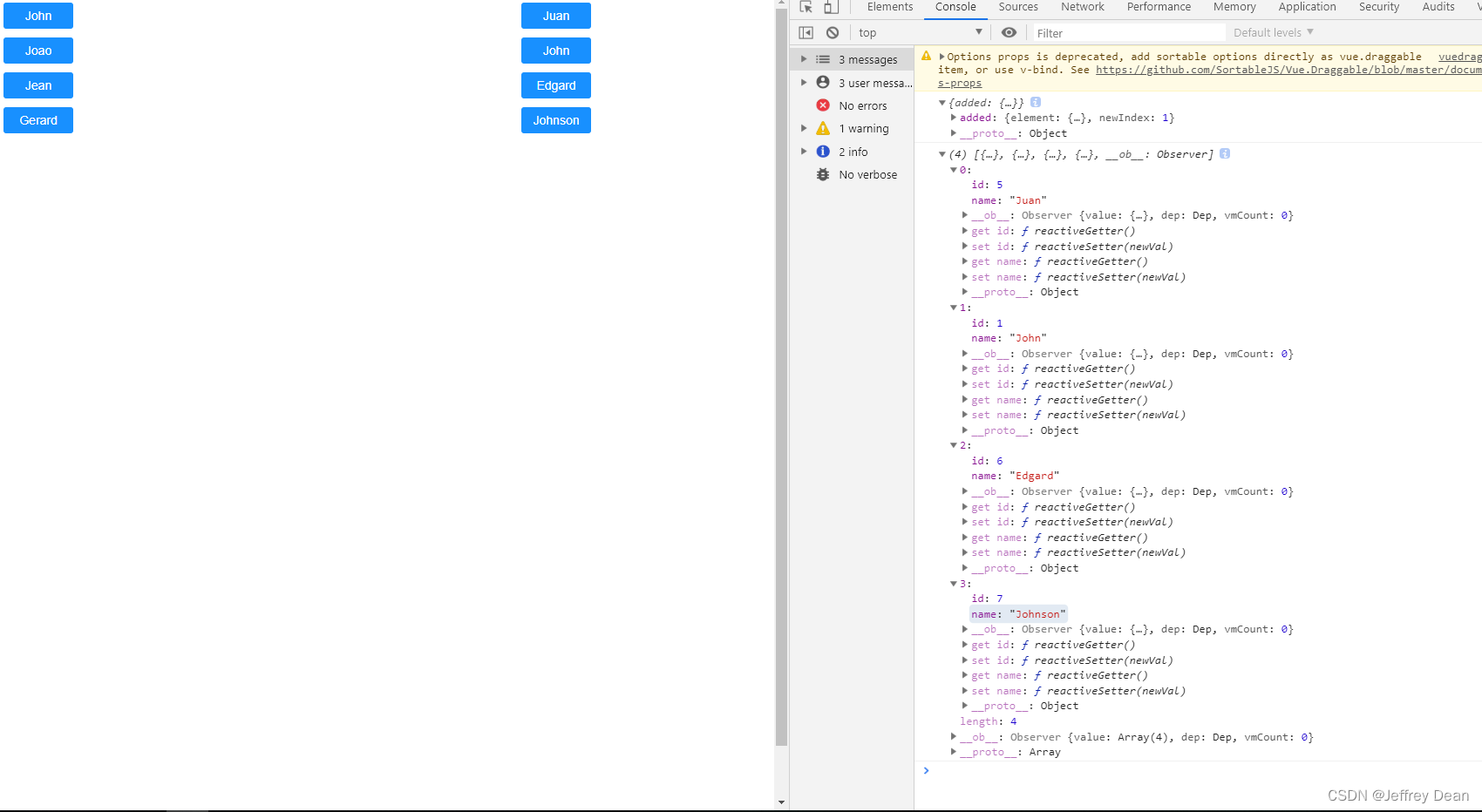
vuedraggable的使用
Draggable为基于Sortable.js的vue组件,用以实现拖拽功能。 特性 支持触摸设备 支持拖拽和选择文本 支持智能滚动 支持不同列表之间的拖拽 不以jQuery为基础 和视图模型同步刷新 和vue2的国度动画兼容 支持撤销操作 当需要完全控制时,可以抛出所有变化 可…...
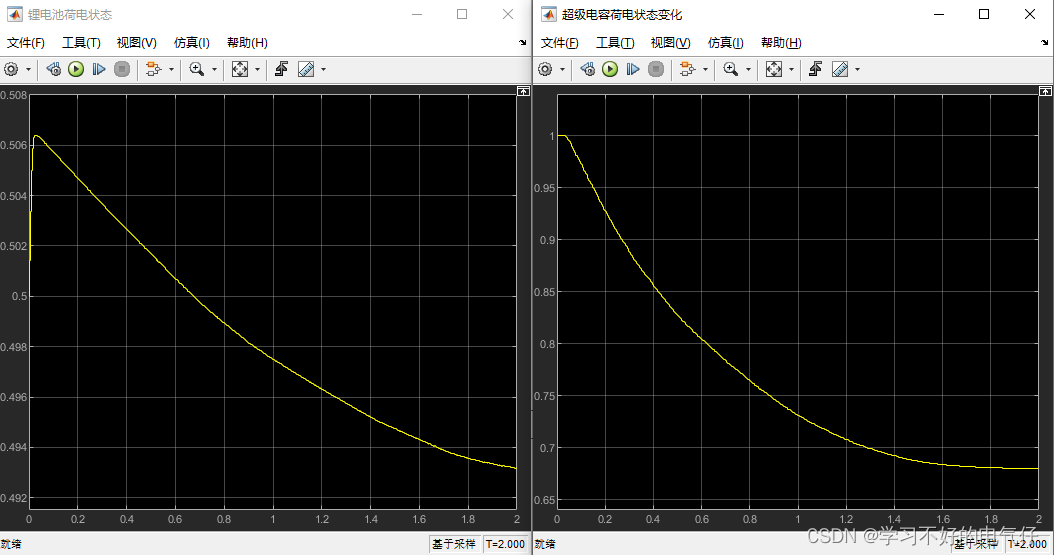
双馈风力发电机-900V直流混合储能并网系统MATLAB仿真
MATLAB2016b主体模型:双馈感应风机模块、采用真实风速数据。混合储能模块、逆变器模块、转子过电流保护模块、整流器控制模块、逆变器控制模块。直流母线电压:有功、无功输出(此处忘记乘负一信号输出),所以是负的。蓄电…...

leader选举过程
启动electionTimer,进行leader选举。 一段时间没有leader和follower通信,就会超时,开始选举leader过程。有个超时时间,如果到了这个时间,就会触发一个回调函数。具体如下: private void handleElectionTimeout() {boo…...

建造者模式
介绍 Java中的建造者模式是一种创建型设计模式,它的主要目的是为了通过一系列简单的步骤构建复杂的对象,允许创建复杂对象的不同表示形式,同时隐藏构造细节.它能够逐步构建对象,即先创建基本对象,然后逐步添加更多属性或部件,直到最终构建出完整的对象. 该模式的主要思想是将…...

IO与NIO区别
一、概念 NIO即New IO,这个库是在JDK1.4中才引入的。NIO和IO有相同的作用和目的,但实现方式不同,NIO主要用到的是块,所以NIO的效率要比IO高很多。在Java API中提供了两套NIO,一套是针对标准输入输出NIO,另一套就是网络编程NIO。 二、NIO和IO的主要区别 下表总结了Java I…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
